5-栈和队列(2)

题一：【用两个栈实现队列】

用两个栈来实现一个队列，完成队列的Push和Pop操作。 队列中的元素为int类型。

分析：栈-先进后出 队列-先进先出

知识点：Stack API

 法一：暴力-一个栈存储push的数据，一个栈pop数据。每次push前将stack2中数据添加到stack1中，每次pop数据前将stack1中数据push到stack2中。

import java.util.Stack;

public class Solution {
    Stack<Integer> stack1 = new Stack<Integer>();
    Stack<Integer> stack2 = new Stack<Integer>();
    
    public void push(int node) {
        while(!stack2.empty()){
            stack1.push(stack2.pop());
        }
        stack1.push(node);
    }
    
    public int pop() {
        while(!stack1.empty()){
            stack2.push(stack1.pop());
        }
        return stack2.pop();
    }
}

 

 法二：没那么麻烦，push时直接将数据添加到stack1中；pop时先判断stack2是否为空，如果不为空直接弹出栈顶元素，如果为空，就将stack1中的元素转移到stack2中，再弹出stack2中的栈顶。

举例：

①{A},{}

②{A B}，{}//直接添加B

③{}，{B}//弹出，stack2为空，将stack1元素转移到stack2中再弹出栈顶

④{C D }，{B}//直接添加 C D

import java.util.Stack;

public class Solution {
    Stack<Integer> stack1 = new Stack<Integer>();
    Stack<Integer> stack2 = new Stack<Integer>();
    
    public void push(int node) {
        stack1.push(node);
    }
    
    public int pop() {
        if(stack2.empty()){
            while(!stack1.empty()){
                stack2.push(stack1.pop());
            }
        }
        return stack2.pop();
    }
}

 

 

---

 

 

题二：【滑动窗口的最大值】

给定一个数组和滑动窗口的大小，找出所有滑动窗口里数值的最大值。例如，如果输入数组{2,3,4,2,6,2,5,1}及滑动窗口的大小3，那么一共存在6个滑动窗口，他们的最大值分别为{4,4,6,6,6,5}； 针对数组{2,3,4,2,6,2,5,1}的滑动窗口有以下6个： {[2,3,4],2,6,2,5,1}， {2,[3,4,2],6,2,5,1}， {2,3,[4,2,6],2,5,1}， {2,3,4,[2,6,2],5,1}， {2,3,4,2,[6,2,5],1}， {2,3,4,2,6,[2,5,1]}。

法一：暴力破解-O(n*size)-看滑动数组大小，太大了效率不行

import java.util.*;
public class Solution {
    public ArrayList<Integer> maxInWindows(int [] num, int size)
    {
        ArrayList<Integer> list = new ArrayList<Integer>();
        if(size<=0) return list;
        for(int left=0,right=size-1;right<num.length;left++,right++){
            int max = num[left];
            for(int i=left+1;i<=right;i++){
                if(num[i]>max) max=num[i];
            }
            list.add(max);
        }
        return list;
    }
}

 

法二：利用双端队列-O(N)

Step1.使用一个双端队列存储滑窗内元素的下标

value	2	3	4	2	6	2	5
index	0	1	2	3	4	5	6

queue

 

 

Step2.若queue为空，说明刚开始滑动，将num第一个元素的索引压入队列中。

value	2	3	4	2	6	2	5
index	0	1	2	3	4	5	6

　queue

0

 

 

Step3.遍历num下一个元素num[1]=3，

　　①先判断当前索引位置减去队列最左边元素是否>=size，如果是，那么说明随着滑窗滑动，当前滑窗内的最大值滑出去了，已经不再这个滑窗内，这是需要将队列最左边元素弹出。（队列最左边为滑窗内最大值索引，判断是否有效）

　　②将当前元素与队列最右边的索引处的数组值对比，如果当前元素大于队列最右边对应的值，则将队列最右边的值弹出，直到找到对应值比当前元素值大的。（队列左边是最大的值，随着上述操作，会逐渐更新队列，滑出去或者新添加的值更大的话将会更新队列，保证队头对应值最大）

value	2	3	4	2	6	2	5
index	0	1	2	3	4	5	6

 

1

 

 

value	2	3	4	2	6	2	5
index	0	1	2	3	4	5	6

 

2

---输出4

 

value	2	3	4	2	6	2	5
index	0	1	2	3	4	5	6

 

2

3

---输出4

 

value	2	3	4	2	6	2	5
index	0	1	2	3	4	5	6

 

4

---输出6

 

value	2	3	4	2	6	2	5
index	0	1	2	3	4	5	6

 

4

5

---输出6

 

value	2	3	4	2	6	2	5
index	0	1	2	3	4	5	6

 

4

5

---输出6

 

value	2	3	4	2	6	2	5	1
index	0	1	2	3	4	5	6	7

 --当前索引处位置（7）-队列最左边（4）=size（3）--》滑出

4

5

7

 --

5

7

 --输出5

 

 

 

 

import java.util.*;
public class Solution {
    public ArrayList<Integer> maxInWindows(int [] num, int size)
    {
        ArrayList<Integer> list = new ArrayList<Integer>();
        if(num==null||size<=0) return list;
        ArrayDeque<Integer> queue = new ArrayDeque<Integer>();
        for(int i=0;i<num.length;i++){
            if(queue.isEmpty()){ //只有i=0，即刚开始遍历时才会为空
                queue.add(i);
            }
            if(i-queue.peekFirst()>=size){//判断队头是否还在滑窗内
                queue.pollFirst();
            }
            while(!queue.isEmpty()&&num[i]>=num[queue.peekLast()]){//排除比新遍历元素还小的对应索引值
                queue.pollLast();
            }
            queue.addLast(i);
            if(i>=size-1){//从第size-1个元素开始，就要输出了
                list.add(num[queue.peekFirst()]);
            }
            
        }
        return list;
    }
}

 

 

 

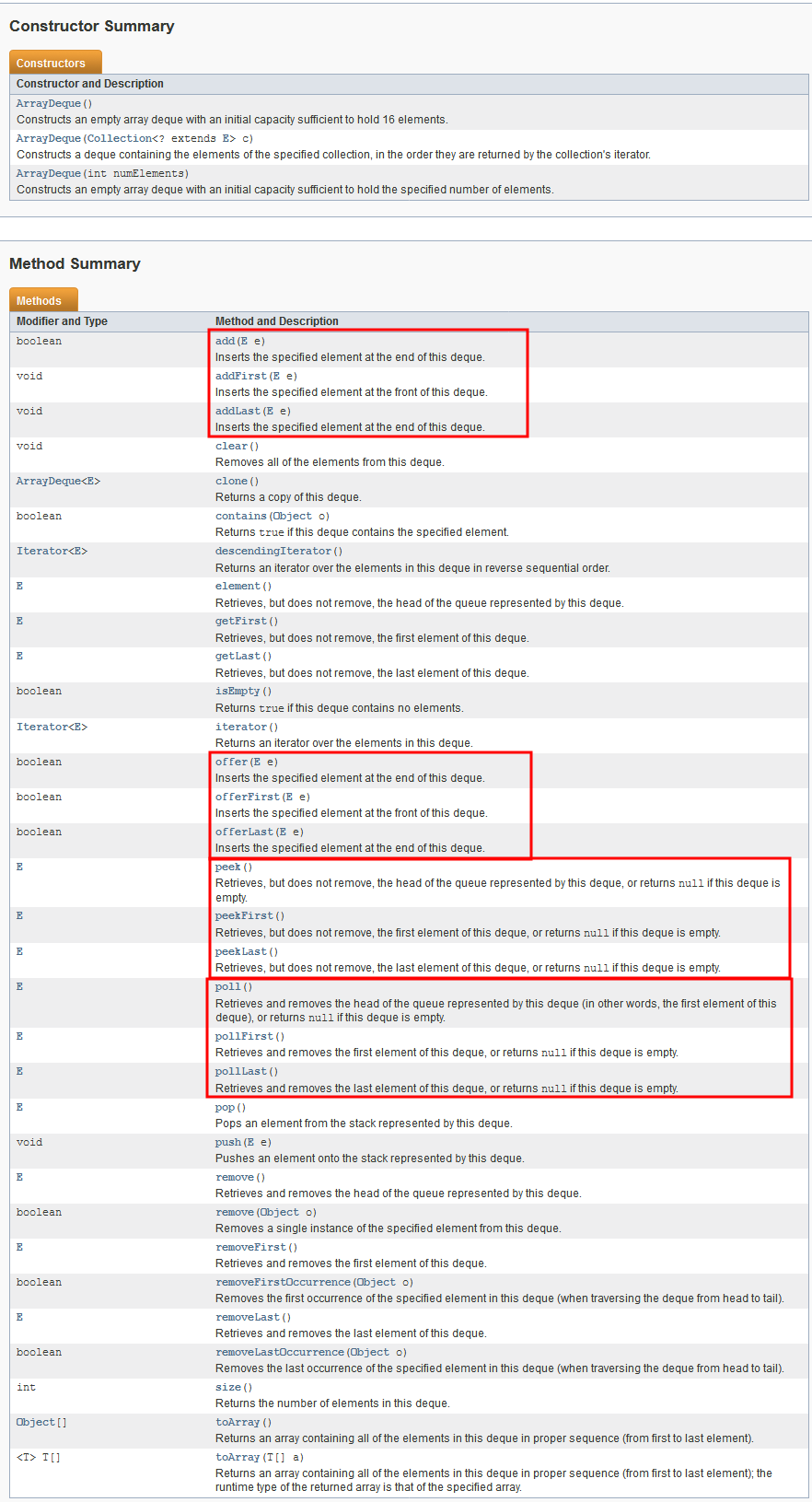
 知识点：ArrayDeque API