4-树篇(8)
题一:【重建二叉树】输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建二叉树并返回。
分析:根据示例可以知道,前序遍历序列第1个为根节点,再根据中序遍历序列可以得到根节点的左右子树{472},{5386};由前序遍历左子树{2 4 7}可以直到左子树根节点为2,再根据中序遍历左子树{472}可以再次分为左右子树……依次递推;
拓展:Arrays.copyOfRange(arr, i, j);复制数组,包括索引i,不包括索引j;
1 /**
2 * Definition for binary tree
3 * public class TreeNode {
4 * int val;
5 * TreeNode left;
6 * TreeNode right;
7 * TreeNode(int x) { val = x; }
8 * }
9 */
10 import java.util.Arrays;
11 public class Solution {
12 public TreeNode reConstructBinaryTree(int [] pre,int [] in) {
13 if(pre.length==0||in.length==0) return null;
14 TreeNode root = new TreeNode(pre[0]);
15 for(int i=0;i<pre.length;i++){
16 if(pre[0]==in[i]){//每次递归到此处,pre,in变成原数组的子集;可重新看作是新的前序后序遍历
17 root.left = reConstructBinaryTree(Arrays.copyOfRange(pre,1,i+1),Arrays.copyOfRange(in,0,i));
18 root.right = reConstructBinaryTree(Arrays.copyOfRange(pre,i+1,pre.length),Arrays.copyOfRange(in,i+1,pre.length));
19 break;
20 }
21 }
22 return root;
23 }
24 }
题二:【二叉树的下一个节点】给定一个二叉树和其中的一个结点,请找出中序遍历顺序的下一个结点并且返回。注意,树中的结点不仅包含左右子结点,同时包含指向父结点的指针。
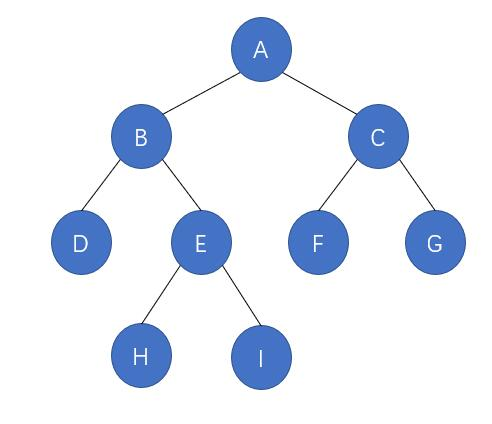
分析:两种情况:当前节点
1.有右节点:判断右节点是否有左子树;①如果有左子树,则返回左子树最左下方节点
②如果没有左子树,则返回右节点
2.没有右节点:判断当前节点是父节点的左孩子还是右孩子;
①如果是左孩子,则返回父节点
②如果是右孩子,向上遍历祖先节点,直到找到一个祖先节点满足为左孩子的条件,返回该祖先节点的父节点,否则返回null了,当前节点为尾节点;
1 /*
2 public class TreeLinkNode {
3 int val;
4 TreeLinkNode left = null;
5 TreeLinkNode right = null;
6 TreeLinkNode next = null;
7
8 TreeLinkNode(int val) {
9 this.val = val;
10 }
11 }
12 */
13 public class Solution {
14 public TreeLinkNode GetNext(TreeLinkNode pNode)
15 {
16 //第一种情况:判断当前节点有右节点(针对从B->H这种情况)
17 if(pNode.right!=null){
18 pNode = pNode.right;
19 while(pNode.left!=null){
20 pNode = pNode.left;
21 }
22 return pNode;
23 }
24 //第二种情况,当前节点没有右节点
25 //判断当前节点是(父节点的)左孩子还是右孩子
26 //1.如果是根节点直接null
27 if(pNode.next==null) return null;
28 //2.如果左孩子
29 if(pNode.next.left==pNode){//如果当前节点是左孩子
30 return pNode.next;//直接返回父节点
31 }
32 //3.如果是右孩子
33 TreeLinkNode pFather = pNode.next;
34 while(pFather.next!=null&&pFather!=pFather.next.left){//向上遍历祖先节点,直到找到一个祖先节点满足为左孩子的条件
35 pFather = pFather.next;
36 }
37 return pFather.next;//返回该祖先节点的父节点
38 }
39 }
题三:【对称二叉树】请实现一个函数,用来判断一颗二叉树是不是对称的。注意,如果一个二叉树同此二叉树的镜像是同样的,定义其为对称的。
分析:使用递归,逐层对比;
关键点:return isSymmetrical(root1.left,root2.right)&&isSymmetrical(root1.right,root2.left); 将root1的左节点和root2的右节点比较,root1的右节点和root2的左节点比较(对称性)
1 /*
2 public class TreeNode {
3 int val = 0;
4 TreeNode left = null;
5 TreeNode right = null;
6
7 public TreeNode(int val) {
8 this.val = val;
9
10 }
11
12 }
13 */
14 public class Solution {
15 boolean isSymmetrical(TreeNode pRoot)
16 {
17 if(pRoot==null) return true;
18 return isSymmetrical(pRoot.left,pRoot.right);
19 }
20 boolean isSymmetrical(TreeNode root1, TreeNode root2){
21 if(root1==null&&root2==null){
22 return true;
23 } else if(root1==null||root2==null){
24 return false;
25 }
26 if(root1.val == root2.val){
27 return isSymmetrical(root1.left,root2.right)&&isSymmetrical(root1.right,root2.left);
28 }else{
29 return false;
30 }
31 }
32 }
题四:【按之字形顺序打印二叉树】请实现一个函数按照之字形打印二叉树,即第一行按照从左到右的顺序打印,第二层按照从右至左的顺序打印,第三行按照从左到右的顺序打印,其他行以此类推。
 A C B D E F G I H
A C B D E F G I H
分析:①奇数行-从左到右遍历放入Stack1中,取出是先遍历右节点,再遍历左节点;(注意:这里是节点存入栈中,并不是取出结果,想要结果正 确,存入栈中得反着存)
②偶数行-从右到左遍历,先存入Stack2中,取出是先遍历左节点,再遍历右节点;
③奇数行or偶数行判断:可设置一个变量isOdd,每次Stack1或者Stack2为空时(这行遍历完了)就递增;
扩展:Stack API

1 import java.util.*;
2
3 /*
4 public class TreeNode {
5 int val = 0;
6 TreeNode left = null;
7 TreeNode right = null;
8
9 public TreeNode(int val) {
10 this.val = val;
11
12 }
13
14 }
15 */
16 public class Solution {
17 public ArrayList<ArrayList<Integer> > Print(TreeNode pRoot) {
18 ArrayList<ArrayList<Integer> > list = new ArrayList<ArrayList<Integer> >();
19 Stack<TreeNode> stack1 = new Stack<TreeNode>();//存放奇数行节点
20 Stack<TreeNode> stack2 = new Stack<TreeNode>();//存放偶数行节点(从0开始计算)
21 stack2.push(pRoot);
22 int isOdd = 1;
23 while(!stack1.empty()||!stack2.empty()){
24 if(isOdd%2!=0){//遍历到奇数行
25 ArrayList<Integer> temp = new ArrayList<Integer>();
26 while(!stack2.empty()){//根据上一行(偶数行)得到奇数层的遍历结果
27 TreeNode node = stack2.pop();
28 if(node!=null){
29 temp.add(node.val);
30 stack1.push(node.left);//先左后右(这里是放入stack中,先进后出,如果想要结果先右后左,就必须反着存入栈中)
31 stack1.push(node.right);
32 }
33 }
34 if(!temp.isEmpty()){
35 list.add(temp);
36 isOdd++;
37 }
38 }else{
39 ArrayList<Integer> temp = new ArrayList<Integer>();
40 while(!stack1.empty()){//根据上一行(偶数行)得到奇数层的遍历结果
41 TreeNode node = stack1.pop();
42 if(node!=null){
43 temp.add(node.val);
44 stack2.push(node.right);
45 stack2.push(node.left);
46 }
47 }
48 if(!temp.isEmpty()){
49 list.add(temp);
50 isOdd++;
51 }
52 }
53 }
54 return list;
55 }
56 }
题五:【把二叉树打印成多行】从上到下按层打印二叉树,同一层结点从左至右输出。每一层输出一行。
分析:层序遍历BST-使用队列;(我的方法是利用题四思想,直接使用两个队列完成,相较于题四难度降低)
注意:本题难点在于解决层数信息
拓展:队列API
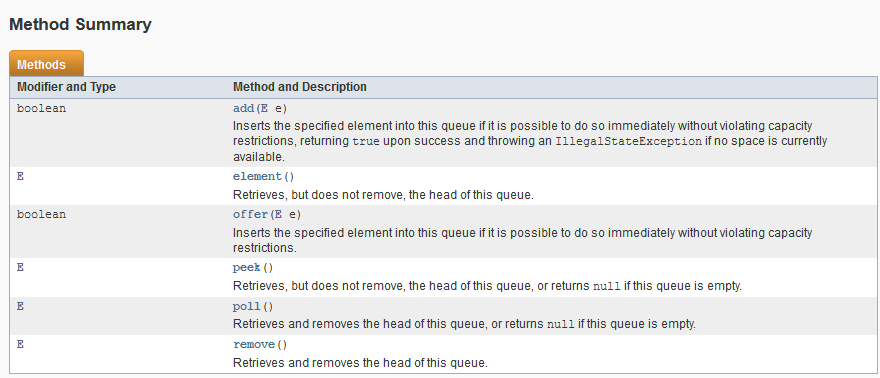
1 import java.util.*;
2
3
4 /*
5 public class TreeNode {
6 int val = 0;
7 TreeNode left = null;
8 TreeNode right = null;
9
10 public TreeNode(int val) {
11 this.val = val;
12
13 }
14
15 }
16 */
17 public class Solution {
18 ArrayList<ArrayList<Integer> > Print(TreeNode pRoot) {
19 ArrayList<ArrayList<Integer> > list = new ArrayList<ArrayList<Integer> >();
20 Queue<TreeNode> queue1 = new LinkedList<TreeNode>();
21 Queue<TreeNode> queue2 = new LinkedList<TreeNode>();
22 queue1.offer(pRoot);
23 int isOdd = 0;//层数
24 while(queue1.size()!=0||queue2.size()!=0){
25 if(isOdd%2==0){
26 ArrayList<Integer> temp = new ArrayList<Integer>();
27 while(queue1.size()!=0){
28 TreeNode node = queue1.poll();
29 if(node!=null){
30 temp.add(node.val);
31 queue2.offer(node.left);
32 queue2.offer(node.right);
33 }
34 }
35 if(!temp.isEmpty()){
36 isOdd++;
37 list.add(temp);
38 }
39 }else{
40 ArrayList<Integer> temp = new ArrayList<Integer>();
41 while(queue2.size()!=0){
42 TreeNode node = queue2.poll();
43 if(node!=null){
44 temp.add(node.val);
45 queue1.offer(node.left);
46 queue1.offer(node.right);
47 }
48 }
49 if(!temp.isEmpty()){
50 isOdd++;
51 list.add(temp);
52 }
53 }
54 }
55 return list;
56 }
57 }
题六:【序列化二叉树】请实现两个函数,分别用来序列化和反序列化二叉树
二叉树的反序列化是指:根据某种遍历顺序得到的序列化字符串结果str,重构二叉树。
1 /*
2 public class TreeNode {
3 int val = 0;
4 TreeNode left = null;
5 TreeNode right = null;
6
7 public TreeNode(int val) {
8 this.val = val;
9
10 }
11
12 }
13 */
14 import java.util.*;
15 public class Solution {
16 String Serialize(TreeNode root) {
17 //前序遍历
18 if(root==null){
19 return "#!";
20 }
21 String str = root.val+"!";
22 str += Serialize(root.left);
23 str += Serialize(root.right);
24 return str;
25 }
26 /**
27 * 将序列化字符串装入一个queue中
28 */
29 TreeNode Deserialize(String str) {
30 Queue<String> queue = new LinkedList<>();
31 Collections.addAll(queue, str.split("!"));
32 return Deserialize(queue);
33 }
34 TreeNode Deserialize(Queue<String> queue) {
35 String str = queue.poll();
36 if(str.equals("#")){
37 return null;
38 }
39 TreeNode root = new TreeNode(Integer.parseInt(str));
40 root.left = Deserialize(queue);
41 root.right = Deserialize(queue);
42 return root;
43 }
44 }
题七:【二叉搜索树的第k个节点】给定一棵二叉搜索树,请找出其中的第k小的结点。例如, (5,3,7,2,4,6,8) 中,按结点数值大小顺序第三小结点的值为4。
分析:使用中序遍历二叉搜索树,放在集合里,根据k值直接取出
1 /*
2 public class TreeNode {
3 int val = 0;
4 TreeNode left = null;
5 TreeNode right = null;
6
7 public TreeNode(int val) {
8 this.val = val;
9
10 }
11
12 }
13 */
14 import java.util.*;
15 public class Solution {
16 ArrayList<TreeNode> list = new ArrayList<TreeNode>();
17 TreeNode KthNode(TreeNode pRoot, int k)
18 {
19 if(k<=0) return null;
20 KthNode(pRoot);
21 if(list.size()<k) return null;
22 return list.get(k-1);
23 }
24 void KthNode(TreeNode node){
25 if(node==null) return;
26 KthNode(node.left);
27 list.add(node);
28 KthNode(node.right);
29 }
30 }
题八:【数据流中的中位数】
如何得到一个数据流中的中位数?如果从数据流中读出奇数个数值,那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值,那么中位数就是所有数值排序之后中间两个数的平均值。我们使用Insert()方法读取数据流,使用GetMedian()方法获取当前读取数据的中位数。
用例:[5,2,3,4,1,6,7,0,8] 对应输出应该为:"5.00 3.50 3.00 3.50 3.00 3.50 4.00 3.50 4.00 "
分析:暴力破解-使用集合存储输入,之后排序,最后直接跟据索引取出结果
1 import java.util.*;
2 public class Solution {
3 ArrayList<Integer> list = new ArrayList<Integer>();
4 public void Insert(Integer num) {
5 list.add(num);
6 }
7
8 public Double GetMedian() {
9 int len = list.size();
10 Collections.sort(list);
11 if(len%2!=0){
12 return Double.valueOf(list.get(len/2));
13 }else{
14 int index1 = (len-1)/2;
15 return (Double.valueOf(list.get(index1))+Double.valueOf(list.get(index1+1)))/2;
16 }
17 }
18 }
分析:中位数左边都是比中位数小的数,右边都是比中位数大的数。可以使用大顶堆存放左边的数据,小顶堆存放右边的数据。可以快速的找到左边的最大值和右边的最小值(堆顶元素)。往堆中插入数据时间复杂度O(logn),得到堆顶元素时间复杂度O(1)。
注意:保证大顶堆和小顶堆的数目之差不能超过1,并且保证大顶堆的数据小于小顶堆的数据。如果插入一个数比大顶堆的数据小,则将此数据加入大顶堆,并将大顶堆堆顶数据加入到小顶堆,反之亦然。
拓展:PriorityQueue API
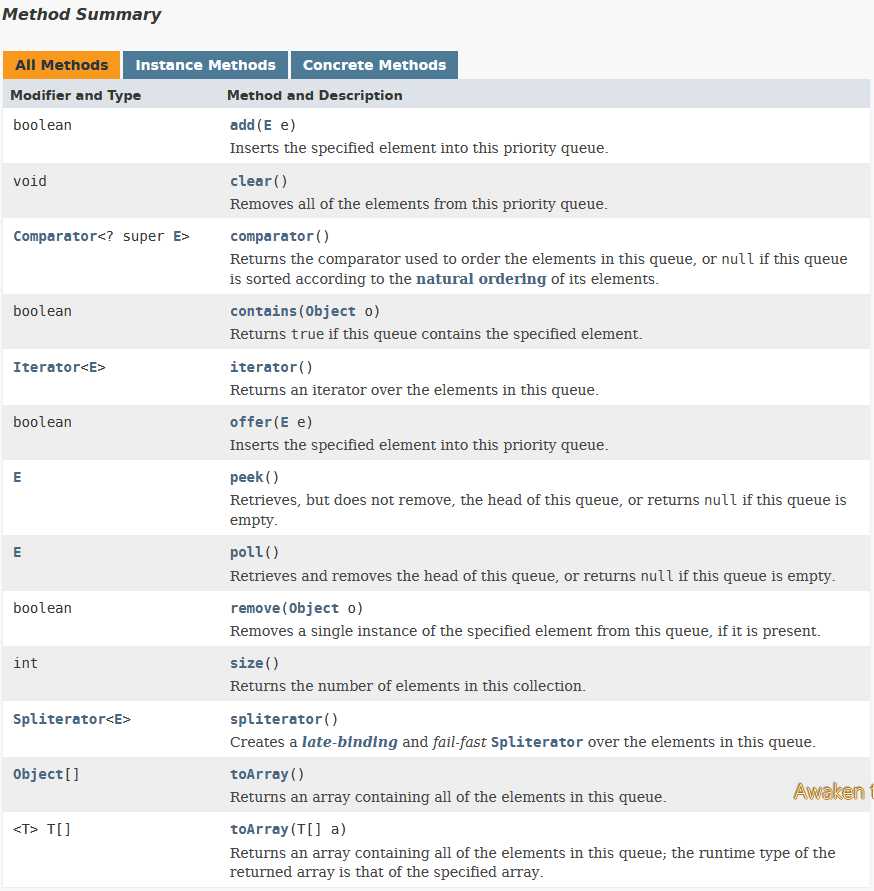
1 import java.util.Comparator;
2 import java.util.PriorityQueue;
3 public class Solution {
4 PriorityQueue<Integer> minQueue = new PriorityQueue<Integer>();
5 PriorityQueue<Integer> maxQueue = new PriorityQueue<Integer>(new Comparator<Integer>(){
6 public int compare(Integer o1, Integer o2){
7 //PriorityQueue默认是小顶堆,实现大顶堆,需要反转默认排序器
8 return o2-o1;
9 }
10 });
11 int count = 0;//数据总数量
12 public void Insert(Integer num) {
13 count++;
14 //数据必须在大顶堆和小顶堆中各倒一次,保证大顶堆的数据都比小顶堆的数据小;
15 if(count%2!=0){//奇数,添加到大顶堆,然后将大顶堆的堆顶添加到小顶堆
16 maxQueue.offer(num);
17 minQueue.offer(maxQueue.poll());
18 }else{//偶数,添加到小顶堆,并将小顶堆堆顶数据添加到大顶堆
19 minQueue.offer(num);
20 maxQueue.offer(minQueue.poll());
21 }
22 }
23 //可使用示例分析
24 public Double GetMedian() {
25 if(count%2!=0){//如果是奇数
26 return Double.valueOf(minQueue.peek());
27 }else{
28 return Double.valueOf((minQueue.peek()+maxQueue.peek()))/2;
29 }
30 }
31 }




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步