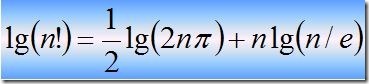学习大数阶乘
Table of Contents
本文应用自liangbch的系列文章 大数阶乘之计算从入门到精通 ,按照自己的习惯整理记录了其中的知识点,只作为学习的总结。版权归liangbch所有。
1 计算阶数比较低的阶乘(factorial)
1.1 迭代法实现
/* 利用 迭代 来计算整数n的阶乘 */ long factorial_iteration( int n ){ int result = 1; while( n>1 ){ result *=n; n--; } return result; }
1.2 递归(recursion)调用实现
/* 利用 递归 来计算整数n的阶乘 */ long factorial_recursion( int n ){ if( n<=0 ){ return 1; }else{ return n*factorial_recutsion( n-1 ); } }
2 大数在计算机语言表示
在日常生活中,我们使用的阿拉伯数字只有0-9共10个,按照书写习惯,一个字符表示1位数字。计算机中, 我们常用的最小数据存储单位是字节,C语言称之为char,多个字节可表示一个更大的存储单位。习惯上,两个 相邻字节组合起来称作一个短整数,在32位的C语言编译器中称之为short,汇编语语言一般记作word,4个相邻 的字节组合起来称为一个长整数,在32位的C语言编译器中称之为long,汇编语言一般记作DWORD。在计算机中, 按照权的不同,数的表示可分为两种,2进制和10进制,严格说来,应该是2k 进制和10K 进制,前者具占用空 间少,运算速度快的优点。后者则具有容易显示的优点。我们试举例说明:
- 若一个大数用一个长为len的short型数组A来表示,并采用权从大到小的顺序依次存放,数N表示为A[ 0 ] * 65536(len-1)+A[ 1 ] * 65536(len-2)+…A[len-1] * 655360,这时65536称为基,其进制2的16次方。
- 若一个大数用一个长为len的short型数组A来表示并采用权从大到小的顺序依次存放,数N=A[ 0 ]*10000(len-1)+A[ 1 ] * 10000(len-2)+…A[len-1] * 100000,这里10000称为基,其进制为10000, 即: 104 ,数组的每个元素可表示4位数字。一般地,这时数组的每一个元素为小于10000的数。类似的,可以用
long型数组,基为2^32=4294967296来表示一个大数; 当然可以用long型组,基为1000000000来表示,这种 表示法,数组的每个元素可表示9位数字。当然,也可以用char型数组,基为10。最后一种表示法,在新手写 的计算大数阶乘程序最为常见,但计算速度却是最慢的。使用更大的基,可以充分发挥CPU的计算能力,计算 量将更少,计算速度更快,占用的存储空间也更少。
3 确定n!有多少位
3.1 简单的近似
n!有多少位数呢?我们给出一个近似的上限值:n! <(n+2)/2的n次方,下面是推导过程。
Caes 1: n是奇数,则中间的那个数mid= (n+1)/2, 除了这个数外,我们可以将1到n之间的数分成n/2组,每组的两 个数为mid-i和mid+i (i=1到mid-1),如1,2,3,4,5,6,7 可以分为数4,和3对数,它们是(3,5),(2,6)和(1,7),容易 知道,每对数的积都于小mid*mid,故n!小于(n+1)/2 的n的次方。
Case 2: n 是个偶数,则中间的两个数n/2和(n+2)/2, 我们将(n+2)/2记做mid,则其它的几对数是(mid-2,mid+1), (mid-3)(mid+2) 等等,容易看出,n!小于mid 的n次方。由以上两种情况可知,对于任意大于1的正整数n, n!<(n+2)/2的n次方。
4 大数阶乘实例
5 实例
5.1 通过char数组
#include "stdio.h" #include "stdlib.h" #include "memory.h" #include "math.h" #include "malloc.h" voidcalcFac
(unsigned long n) { unsigned long i,j,head,tail; int blkLen=(int)(n*log10((n+1)/2)); //计算n!有数数字的个数 blkLen+=4; //保险起见,多加4位 if (n<=1) { printf("%d!=0/n",n); return;} char *arr=(char *)malloc(blkLen); if (arr==NULL) { printf("alloc memory fail/n"); return ;} memset(arr,0,sizeof(char)*blkLen); head=tail=blkLen-1; arr[tail]=1; for (i=2;i<=n;i++) { unsigned long c=0; for (j=tail;j>=head;j--) { unsigned long prod=arr[j] * i +c; arr[j]=(char)( prod % 10); c= prod / 10; } while (c>0) { head--; arr[head]=(char)(c % 10); c/=10; } } printf("%d!=",n); for (i=head;i<=tail;i++) printf("%c",arr[i]+'0'); printf("\n"); free(arr); } void testCalcFac() { int n; while (1) { printf("n=?"); scanf("%ld",&n); if (n==0) break; calcFac(n); } } int main(int argc, char* argv[]) { testCalcFac(); return 0; }
5.2 改进程序
上面给出一个计算阶乘的程序,它采用char型数组存贮大数,1个元素表示1位十进制数字,在计算时,一次乘法可计算一位数字和一个整数的乘积。该算法具有简单直观的优点,但缺点也是明显的,速度不快,占用内存空间也较多,本文将给出一个改后的程序,有效的克服了这些缺点。
在32位c语言编译器中,unsigned long(DWORD)型变量可以表示一个32bit的整数,unsigned short(WORD)型变量可表示一个16bit的整数。两个65535以内的数相乘,其结果完全可以存贮在一个unsigned long变量中。另外,在好多32位编译器中,也提供了64bit的整数类型(如在VC中,unsigned __ int64可表示一个64bit的整数,在GCC中, long long可表示一个64位的整数)。同理两个40亿以内的数相乘,其结果可以用一个unsigned __ int64 型的变量来存储。让一个具有一次可计算两个32bit数乘法能力的CPU一次只计算1个1位10进制数和一个整数的乘法,实在是一种浪费。下面我们提出两种大数的表示法和运算方法。
5.2.1 改进算法1
第一种方法:用WORD型数组表示大数,用DWORD型变量表示两个WORD型变量的乘积。
数组的每个元素表示4位十进制数。在运算时,从这个数的最后一个元素开始,依次乘以当前乘数并加上上次的进位,其和的低4位数依然存在原位置,高几位向前进位。当乘数i小于42万时,其乘积加上进位可以用一个DWORD型变量表示,故这个程序可以计算上到42万的阶乘。
#include "stdlib.h" #include "stdio.h" #include "math.h" #define PI 3.1415926535897932384626433832795 #define RAD 10000 typedef unsigned long DWORD; typedef unsigned short WORD; //用stirling公式估算结果长度,稍微算得大一点 DWORD calcResultLen(DWORD n,DWORD rad) { double r=0.5*log(2*PI) + (n+0.5)*log(n)-n; return (DWORD)(r/log(rad)+2); } void calcFac1(DWORD n) { DWORD i,carry,prod,len; WORD *buff,*pHead,*pTail,*p; if (n==0) { printf("%d!=1",n); return; } //---计算并分配所需的存储空间 len=calcResultLen(n,RAD); buff=(WORD*)malloc( sizeof(WORD)*len); if (buff==NULL) return ; //以下代码计算n! pHead=pTail=buff+len-1; for (*pTail=1,i=2;i<=n;i++) { for (carry=0,p=pTail;p>=pHead;p--) { prod=(DWORD)(*p) * i +carry; *p=(WORD)(prod % RAD); carry=prod / RAD; } while (carry>0) { pHead--; *pHead=(WORD)(carry % RAD); carry /= RAD; } } //显示计算结果 printf("%d!=%d",n,*pHead); for (p=pHead+1;p<=pTail;p++) printf("%04d",*p); printf("\n"); free(buff);//释放分配的内存 } int main(int argc, char* argv[]) { DWORD n; printf("please input n:"); scanf("%d",&n); calcFac1(n); return 0; }
5.2.2 改进算法2
第二种方法:用DWORD型数组表示大数,用unsigned __int64 表示两个DWORD型变量的乘积。
从算法上讲,这个程序能够计算到40亿的阶乘,在实际计算过程中,仅受限于内存的大小。至于速度,比前一个程序要慢一些,原因在于unsigned __int64的除法较慢。
#define TEN9 1000000000 void calcFac2(DWORD n) { DWORD *buff,*pHead,*pTail,*p; DWORD t,i,len; UINT64 carry,prod; if (n==0) { printf("%d!=1",n); return; } //---计算并分配所需的存储空间 t=GetTickCount(); len=calcResultLen(n,TEN9); buff=(DWORD*)malloc( sizeof(DWORD)*len); if (buff==NULL) return ; //以下代码计算n! pHead=pTail=buff+len-1; for (*pTail=1,i=2;i<=n;i++) { for (carry=0,p=pTail;p>=pHead;p--) { prod=(UINT64)(*p) * (UINT64)i +carry; *p=(DWORD)(prod % TEN9); carry=prod / TEN9; } while (carry>0) { pHead--; *pHead=(DWORD)(carry % TEN9); carry /= TEN9; } } t=GetTickCount()-t; //显示计算结果 printf("It take %d ms/n",t); printf("%d!=%d",n,*pHead); for (p=pHead+1;p<=pTail;p++) printf("%09d",*p); printf("\n"); free(buff);//释放分配的内存 }