求质数-埃拉托斯特尼筛法
Table of Contents
1 质数
质数又称素数。指在一个大于1的自然数中，除了1和此整数自身外，没法被其他自然数整除的数。换句话说，只有两个正因数（1和自己）的自然数即为素数。比1大但不是素数的数称为合数。1和0既非素数也非合数。合数是由若干个质数相乘而得到的。
2 求质数的方法
主要有两种方法：试除法和筛选法（主要是埃拉托斯特尼筛法）。
2.1 试除法
试除法想必大家都很熟悉，这里就不论述了。
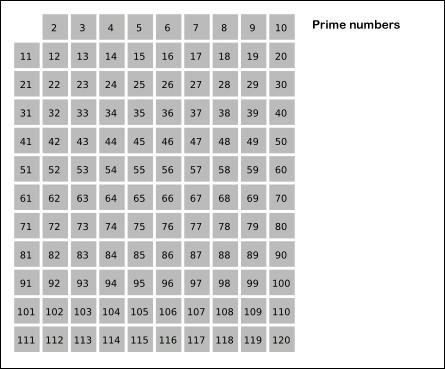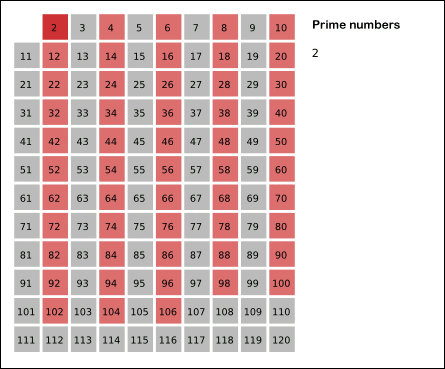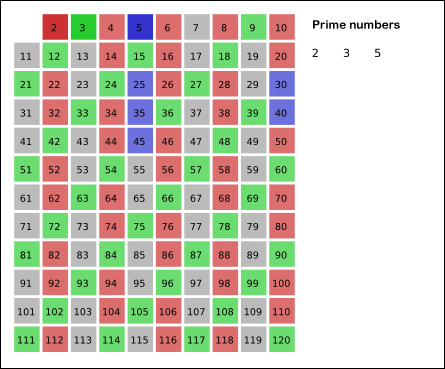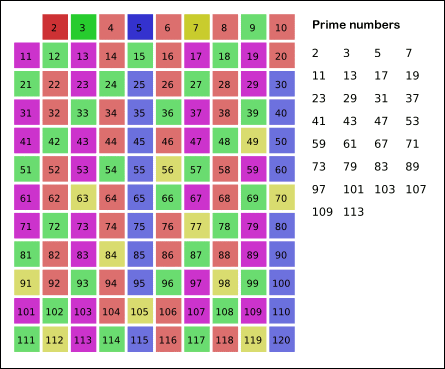
2.2 埃拉托斯特尼筛法
解释不容易懂，大家可以看一张维基百科上的图：
2.2.1 程序实现
若i为素数，则设置a[i]为1；反之则设置为0。首先，将所有数组的元素设置为1，表示没有已知的非素数。然后将已知为非素数（即为已知素数的倍数）的索引对应的数组元素设置为0。如果将所有较小的素数的倍数都设置为0之后，a[i]仍然保持为1，则可判断它是所找的素数。
#define N 10000 int main() { int i, j, a[N]; for (i = 2; i < N; i++) a[i] = 1; for (i = 2; i < N; i++) if (a[i]) for (j = i; j < N/i; j++) a[i*j] = 0; for (i = 2; i < N; i++) if (a[i]) printf("%4d ", i); printf("\n"); return 0; }
如果上面的数组变为bool型或者是位的话，更能节省空间，获得更高的空间有效性。
要计算更大的质数，上面的程序需要重新编译。我们可以动态的分配内存，从命令行取得最大值的期望。如下：
int main(int argc, char *argv[]) { long int i, j, N = atoi(argv[1]); int *a = malloc(N*sizeof(int)); if (a == NULL) { printf("Insufficient memory.\n"); return; } ...
