连通性（connectivity）问题
Table of Contents
1 本文参考
- 《Algorithms In C》，Robert Sedgewick.
2 连通性问题描述
2.1 问题数学示例
假设有个整数对，p-q解释为p与q连通。如图 
如果新输入的对，可以由以前的输入对连通，就不会输出；如果不能由以前的对连通，就输出这个对。例如2-9不在输出之列，因为前面的对存在2-3-4-9的连通。
2.2 应用示例
- 整数代表网络节点，对代表网络连通，因此网络可以判断p和q之间是否应经连通。
- 电网
- 更甚至与程序中定义的两个等价变量
3 算法实现
首先假设连通的每个节点都存在一个数组中a[N],没次都选择两个节点，判断两个节点是不是连通。
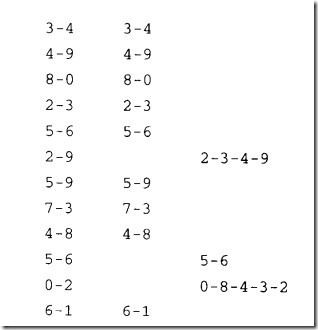
3.1 快速查找（quick-find）算法
程序中当且仅当p与q连通的时候，id[p]与id[q]相等。
1: #include <stdio.h> 2: #define N 10 3: int main(int argc, char *argv[]) 4: { 5: int count; 6: int i=0,p,q,t,id[N]; 7: for (i=0; i < N; ++i) 8: { 9: id[i]=i; 10: } 11: while(scanf("%d %d",&p,&q)==2) 12: { 13: if(id[p]==id[q]) continue; 14: count=0; 15: for(t=id[p],i=0;i<N;++i) 16: { 17: if (t==id[i]) 18: { 19: count++; 20: id[i]=id[q]; 21: } 22: } 23: printf("\n%d-%d\n",p,q); 24: for (i=0; i < N; ++i) 25: { 26: printf("%d ",id[i]); 27: } 28: } 29: return 0; 30: }
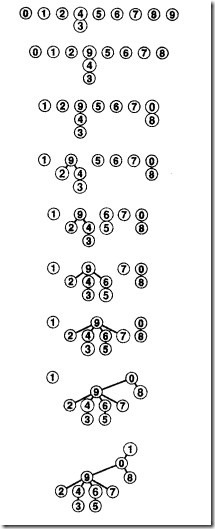
3.2 快速并集算法
相比上面的算法，并集运算计算量少，查找运算计算量大，算是算法的改进。根本就是：每个节点都沿着树上移，找到各自的根节点(root)。
1: #include <stdio.h> 2: #define N 10 3: int main(int argc, char *argv[]) 4: { 5: int i,j; 6: int p,q; /* 输入的连通对 */ 7: int id[N]; 8: for (i = 0; i < N; ++i) 9: { 10: id[i]=i; 11: } 12: while(scanf("%d %d",&p,&q)==2) 13: { 14: for(i=p;i!=id[i];i=id[i]); 15: for(j=q;j!=id[j];j=id[j]); 16: if(i==j) continue; 17: id[i]=j; 18: printf("\n%d-%d\n",p,q); 19: for (i=0; i < N; ++i) 20: { 21: printf("%d ",id[i]); 22: } 23: } 24: printf("\n"); 25: return 0; 26: }
结果图解如下：
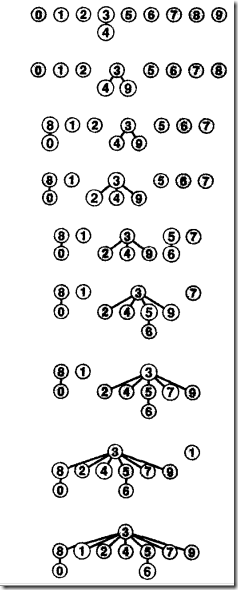
3.3 快速并集的加权算法
上面的算法，我们并不能保证每一种情况，它的速度都比快速查找有实质性的提高。这个是修改版，它使用一个额外的数组sz完成维护的目的，为每个对象用id[i]==i来表示，这样可以组织树的增长。下图描述了快速并集加权算法，连接两棵树的时候，较小的数的根要附属到较大的数的根下面。这样节点与根的距离短，多以查找效率要高：
3.4 对分路径压缩-快速并集的加权算法（部分）
这个比全路径压缩算法简单:然每个节点在连通的过程中，跳到上一级树，指向上一级的节点，从而实现路径压缩。与上个算法相比，改进：
for(i=p;i!=id[i];i=id[i]) id[i]=id[id[i]]; for(j=q;j!=id[j];j=id[j]) id[j]=id[id[j]];
如图，当处理1和6的时候，让1、5、6都指向3，得到的树比上面的算法更扁平。
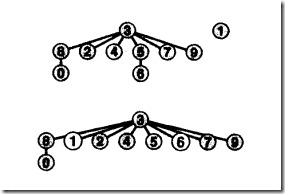
3.5 全路径压缩-快速并集的加权算法
1: #include <stdio.h> 2: #include <stdlib.h> 3: #define BUFFER_MAX_SIZE 16 4: int main(int argc, char *argv[]) { 5: size_t con[BUFFER_MAX_SIZE]; 6: size_t con_cnt[BUFFER_MAX_SIZE]; 7: size_t elem[BUFFER_MAX_SIZE][BUFFER_MAX_SIZE]; 8: size_t elem_cnt[BUFFER_MAX_SIZE]; 9: size_t p, q, r, i, j, k; 10: for(r=0; r<BUFFER_MAX_SIZE; r++) { 11: con[r]=r; 12: con_cnt[r]=1; 13: elem[r][0]=r; 14: elem_cnt[r]=1; 15: } 16: 17: while(scanf("%d-%d", &p, &q)==2) { 18: if(p>=BUFFER_MAX_SIZE||q>=BUFFER_MAX_SIZE) 19: exit(EXIT_FAILURE); 20: for(i=p; i!=con[i]; i=con[i]); 21: for(j=q; j!=con[j]; j=con[j]); 22: if(i==j) 23: continue; 24: if(con_cnt[i]<con_cnt[j]) { 25: k=elem_cnt[j]; 26: for(r=0; r<elem_cnt[i]; r++) 27: elem[j][elem_cnt[j]++]=elem[i][r]; 28: for(r=k; r<elem_cnt[j]; r++) 29: con[elem[j][r]]=j; 30: con_cnt[j]+=con_cnt[i]; 31: } 32: else { 33: k=elem_cnt[i]; 34: for(r=0; r<elem_cnt[j]; r++) 35: elem[i][elem_cnt[i]++]=elem[j][r]; 36: for(r=k; r<elem_cnt[i]; r++) 37: con[elem[i][r]]=i; 38: con_cnt[i]+=con_cnt[j]; 39: } 40: printf("%d-%d\n", p, q); 41: for(r=0; r<BUFFER_MAX_SIZE; r++) 42: printf("%d\t", con[r]); 43: printf("\n"); 44: } 45: exit(EXIT_SUCCESS); 46: }
