海量数据中找出前k大数（topk问题）
前两天面试3面学长问我的这个问题（想说TEG的3个面试学长都是好和蔼，希望能完成最后一面，各方面原因造成我无比想去鹅场的心已经按捺不住了），这个问题还是建立最小堆比较好一些。
先拿10000个数建堆，然后一次添加剩余元素，如果大于堆顶的数（10000中最小的），将这个数替换堆顶，并调整结构使之仍然是一个最小堆，这样，遍历完后，堆中的10000个数就是所需的最大的10000个。建堆时间复杂度是O（mlogm），算法的时间复杂度为O（nmlogm）（n为10亿，m为10000）。
优化的方法：可以把所有10亿个数据分组存放，比如分别放在1000个文件中。这样处理就可以分别在每个文件的10^6个数据中找出最大的10000个数，合并到一起在再找出最终的结果。
以上就是面试时简单提到的内容，下面整理一下这方面的问题：
top K问题
针对top K类问题，通常比较好的方案是分治+Trie树/hash+小顶堆（就是上面提到的最小堆），即先将数据集按照Hash方法分解成多个小数据集，然后使用Trie树活着Hash统计每个小数据集中的query词频，之后用小顶堆求出每个数据集中出现频率最高的前K个数，最后在所有top K中求出最终的top K。
eg：有1亿个浮点数，如果找出期中最大的10000个？
最容易想到的方法是将数据全部排序，然后在排序后的集合中进行查找，最快的排序算法的时间复杂度一般为O（nlogn），如快速排序。但是在32位的机器上，每个float类型占4个字节，1亿个浮点数就要占用400MB的存储空间，对于一些可用内存小于400M的计算机而言，很显然是不能一次将全部数据读入内存进行排序的。其实即使内存能够满足要求（我机器内存都是8GB），该方法也并不高效，因为题目的目的是寻找出最大的10000个数即可，而排序却是将所有的元素都排序了，做了很多的无用功。
第二种方法为局部淘汰法，该方法与排序方法类似，用一个容器保存前10000个数，然后将剩余的所有数字——与容器内的最小数字相比，如果所有后续的元素都比容器内的10000个数还小，那么容器内这个10000个数就是最大10000个数。如果某一后续元素比容器内最小数字大，则删掉容器内最小元素，并将该元素插入容器，最后遍历完这1亿个数，得到的结果容器中保存的数即为最终结果了。此时的时间复杂度为O（n+m^2），其中m为容器的大小，即10000。
第三种方法是分治法，将1亿个数据分成100份，每份100万个数据，找到每份数据中最大的10000个，最后在剩下的100*10000个数据里面找出最大的10000个。如果100万数据选择足够理想，那么可以过滤掉1亿数据里面99%的数据。100万个数据里面查找最大的10000个数据的方法如下：用快速排序的方法，将数据分为2堆，如果大的那堆个数N大于10000个，继续对大堆快速排序一次分成2堆，如果大的那堆个数N大于10000个，继续对大堆快速排序一次分成2堆，如果大堆个数N小于10000个，就在小的那堆里面快速排序一次，找第10000-n大的数字；递归以上过程，就可以找到第1w大的数。参考上面的找出第1w大数字，就可以类似的方法找到前10000大数字了。此种方法需要每次的内存空间为10^6*4=4MB，一共需要101次这样的比较。
第四种方法是Hash法。如果这1亿个书里面有很多重复的数，先通过Hash法，把这1亿个数字去重复，这样如果重复率很高的话，会减少很大的内存用量，从而缩小运算空间，然后通过分治法或最小堆法查找最大的10000个数。
第五种方法采用最小堆。首先读入前10000个数来创建大小为10000的最小堆，建堆的时间复杂度为O（mlogm）（m为数组的大小即为10000），然后遍历后续的数字，并于堆顶（最小）数字进行比较。如果比最小的数小，则继续读取后续数字；如果比堆顶数字大，则替换堆顶元素并重新调整堆为最小堆。整个过程直至1亿个数全部遍历完为止。然后按照中序遍历的方式输出当前堆中的所有10000个数字。该算法的时间复杂度为O（nmlogm），空间复杂度是10000（常数）。
实际运行：
实际上，最优的解决方案应该是最符合实际设计需求的方案，在时间应用中，可能有足够大的内存，那么直接将数据扔到内存中一次性处理即可，也可能机器有多个核，这样可以采用多线程处理整个数据集。
下面针对不容的应用场景，分析了适合相应应用场景的解决方案。
（1）单机+单核+足够大内存
如果需要查找10亿个查询次（每个占8B）中出现频率最高的10个，考虑到每个查询词占8B，则10亿个查询次所需的内存大约是10^9 * 8B=8GB内存。如果有这么大内存，直接在内存中对查询次进行排序，顺序遍历找出10个出现频率最大的即可。这种方法简单快速，使用。然后，也可以先用HashMap求出每个词出现的频率，然后求出频率最大的10个词。
（2）单机+多核+足够大内存
这时可以直接在内存总使用Hash方法将数据划分成n个partition，每个partition交给一个线程处理，线程的处理逻辑同（1）类似，最后一个线程将结果归并。
该方法存在一个瓶颈会明显影响效率，即数据倾斜。每个线程的处理速度可能不同，快的线程需要等待慢的线程，最终的处理速度取决于慢的线程。而针对此问题，解决的方法是，将数据划分成c×n个partition（c>1），每个线程处理完当前partition后主动取下一个partition继续处理，知道所有数据处理完毕，最后由一个线程进行归并。
（3）单机+单核+受限内存
这种情况下，需要将原数据文件切割成一个一个小文件，如次啊用hash(x)%M，将原文件中的数据切割成M小文件，如果小文件仍大于内存大小，继续采用Hash的方法对数据文件进行分割，知道每个小文件小于内存大小，这样每个文件可放到内存中处理。采用（1）的方法依次处理每个小文件。
（4）多机+受限内存
这种情况，为了合理利用多台机器的资源，可将数据分发到多台机器上，每台机器采用（3）中的策略解决本地的数据。可采用hash+socket方法进行数据分发。
从实际应用的角度考虑，（1）（2）（3）（4）方案并不可行，因为在大规模数据处理环境下，作业效率并不是首要考虑的问题，算法的扩展性和容错性才是首要考虑的。算法应该具有良好的扩展性，以便数据量进一步加大（随着业务的发展，数据量加大是必然的）时，在不修改算法框架的前提下，可达到近似的线性比；算法应该具有容错性，即当前某个文件处理失败后，能自动将其交给另外一个线程继续处理，而不是从头开始处理。
top K问题很适合采用MapReduce框架解决，用户只需编写一个Map函数和两个Reduce 函数，然后提交到Hadoop（采用Mapchain和Reducechain）上即可解决该问题。具体而言，就是首先根据数据值或者把数据hash(MD5)后的值按照范围划分到不同的机器上，最好可以让数据划分后一次读入内存，这样不同的机器负责处理不同的数值范围，实际上就是Map。得到结果后，各个机器只需拿出各自出现次数最多的前N个数据，然后汇总，选出所有的数据中出现次数最多的前N个数据，这实际上就是Reduce过程。对于Map函数，采用Hash算法，将Hash值相同的数据交给同一个Reduce task；对于第一个Reduce函数，采用HashMap统计出每个词出现的频率，对于第二个Reduce 函数，统计所有Reduce task，输出数据中的top K即可。
直接将数据均分到不同的机器上进行处理是无法得到正确的结果的。因为一个数据可能被均分到不同的机器上，而另一个则可能完全聚集到一个机器上，同时还可能存在具有相同数目的数据。
以下是一些经常被提及的该类问题。
（1）有10000000个记录，这些查询串的重复度比较高，如果除去重复后，不超过3000000个。一个查询串的重复度越高，说明查询它的用户越多，也就是越热门。请统计最热门的10个查询串，要求使用的内存不能超过1GB。
（2）有10个文件，每个文件1GB，每个文件的每一行存放的都是用户的query，每个文件的query都可能重复。按照query的频度排序。
（3）有一个1GB大小的文件，里面的每一行是一个词，词的大小不超过16个字节，内存限制大小是1MB。返回频数最高的100个词。
（4）提取某日访问网站次数最多的那个IP。
（5）10亿个整数找出重复次数最多的100个整数。
（6）搜索的输入信息是一个字符串，统计300万条输入信息中最热门的前10条，每次输入的一个字符串为不超过255B，内存使用只有1GB。
（7）有1000万个身份证号以及他们对应的数据，身份证号可能重复，找出出现次数最多的身份证号。
重复问题
在海量数据中查找出重复出现的元素或者去除重复出现的元素也是常考的问题。针对此类问题，一般可以通过位图法实现。例如，已知某个文件内包含一些电话号码，每个号码为8位数字，统计不同号码的个数。
本题最好的解决方法是通过使用位图法来实现。8位整数可以表示的最大十进制数值为99999999。如果每个数字对应于位图中一个bit位，那么存储8位整数大约需要99MB。因为1B=8bit，所以99Mbit折合成内存为99/8=12.375MB的内存，即可以只用12.375MB的内存表示所有的8位数电话号码的内容。
Top K问题的两种解决思路
Top K问题在数据分析中非常普遍的一个问题（在面试中也经常被问到），比如：
从20亿个数字的文本中，找出最大的前100个。
解决Top K问题有两种思路，
- 最直观：小顶堆（大顶堆 -> 最小100个数）；
- 较高效：Quick Select算法。
LeetCode上有一个问题215. Kth Largest Element in an Array，类似于Top K问题。
1. 堆
小顶堆（min-heap）有个重要的性质——每个结点的值均不大于其左右孩子结点的值，则堆顶元素即为整个堆的最小值。JDK中PriorityQueue实现了数据结构堆，通过指定comparator字段来表示小顶堆或大顶堆，默认为null，表示自然序（natural ordering）。
小顶堆解决Top K问题的思路：小顶堆维护当前扫描到的最大100个数，其后每一次的扫描到的元素，若大于堆顶，则入堆，然后删除堆顶；依此往复，直至扫描完所有元素。Java实现第K大整数代码如下：
public int findKthLargest(int[] nums, int k) {
PriorityQueue<Integer> minQueue = new PriorityQueue<>(k);
for (int num : nums) {
if (minQueue.size() < k || num > minQueue.peek())
minQueue.offer(num);
if (minQueue.size() > k)
minQueue.poll();
}
return minQueue.peek();
}2. Quick Select
Quick Select [1]脱胎于快排（Quick Sort），两个算法的作者都是Hoare，并且思想也非常接近：选取一个基准元素pivot，将数组切分（partition）为两个子数组，比pivot大的扔左子数组，比pivot小的扔右子数组，然后递推地切分子数组。Quick Select不同于Quick Sort的是其没有对每个子数组做切分，而是对目标子数组做切分。其次，Quick Select与Quick Sort一样，是一个不稳定的算法；pivot选取直接影响了算法的好坏，worst case下的时间复杂度达到了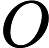
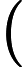
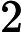
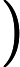O(n2)。下面给出Quick Sort的Java实现：
public void quickSort(int arr[], int left, int right) {
if (left >= right) return;
int index = partition(arr, left, right);
quickSort(arr, left, index - 1);
quickSort(arr, index + 1, right);
}
// partition subarray a[left..right] so that a[left..j-1] >= a[j] >= a[j+1..right]
// and return index j
private int partition(int arr[], int left, int right) {
int i = left, j = right + 1, pivot = arr[left];
while (true) {
while (i < right && arr[++i] > pivot)
if (i == right) break;
while (j > left && arr[--j] < pivot)
if (j == left) break;
if (i >= j) break;
swap(arr, i, j);
}
swap(arr, left, j); // swap pivot and a[j]
return j;
}
private void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}Quick Select的目标是找出第k大元素，所以
- 若切分后的左子数组的长度 > k，则第k大元素必出现在左子数组中；
- 若切分后的左子数组的长度 = k-1，则第k大元素为pivot；
- 若上述两个条件均不满足，则第k大元素必出现在右子数组中。
Quick Select的Java实现如下：
public int findKthLargest(int[] nums, int k) {
return quickSelect(nums, k, 0, nums.length - 1);
}
// quick select to find the kth-largest element
public int quickSelect(int[] arr, int k, int left, int right) {
if (left == right) return arr[right];
int index = partition(arr, left, right);
if (index - left + 1 > k)
return quickSelect(arr, k, left, index - 1);
else if (index - left + 1 == k)
return arr[index];
else
return quickSelect(arr, k - index + left - 1, index + 1, right);
}上面给出的代码都是求解第k大元素；若想要得到Top K元素，仅需要将代码做稍微的修改：比如，扫描完成后的小顶堆对应于Top K，Quick Select算法用中间变量保存Top K元素。
