异常检测

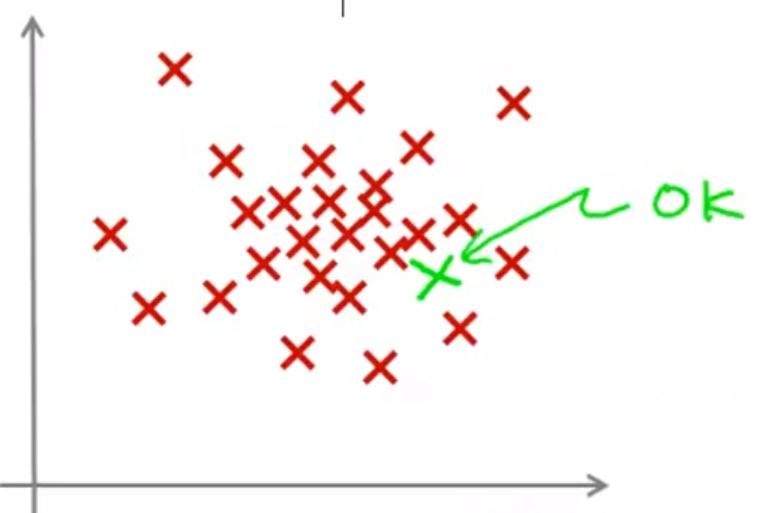
假设你有一些数据如下图

这时，给一个新的数据，我们认为这个数据和原来的数据差距不大，因此认为这个数据时正常的

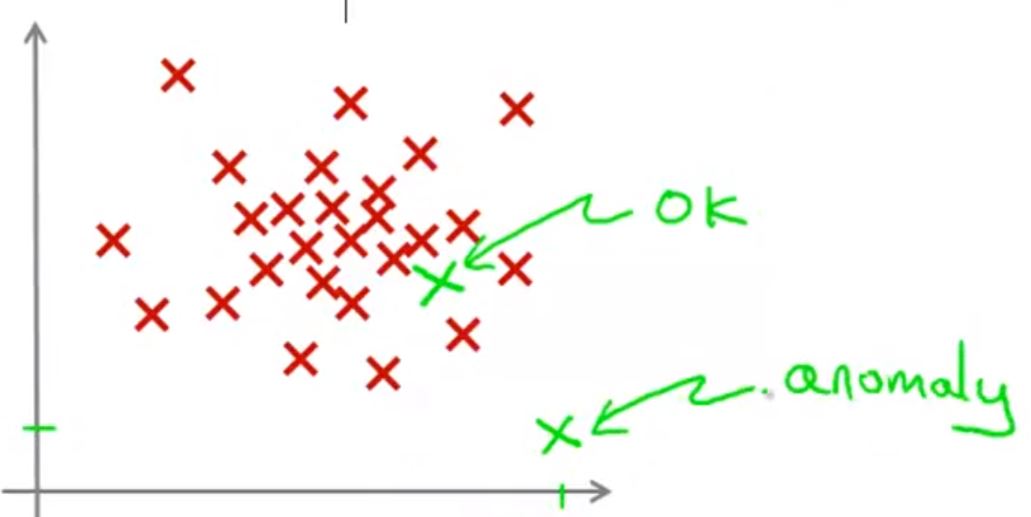
对于下图所示的新数据，我们认为它是“异常点”，因为它距离其他数据较远

---

一般情况下

• 异常检测的训练数据集都是正常/都是不正常的数据
• 然后判断测试数据是否是异常数据

异常检测方法：

• 根据无标签的测试数据建立模型（p(x)）来给出数据正常/不正常的可能性
• 然后将新数据代入模型中计算 p(x)，如果 p(x) < ε ，就将其定义为异常数据；如果 p(x) ≥ ε，就将其定义为正常数据

---

异常检测的例子

欺诈检测：

• x⁽ⁱ⁾ 是第 i 个用户的行为特征
• 建立模型 p(x)
• 运用 p(x_new) 来定义用户是否有可能欺诈

用于制造业：

监控数据中心的计算机

• x⁽ⁱ⁾ 是第 i 个计算机的特征

---

高斯分布（复习）

高斯分布用

\[N\left( {\mu ,{\sigma ^2}} \right)\]

表示，其中 μ 称为均值，σ 称为标准差。表征 x 服从高斯分布用

\[x \sim N\left( {\mu ,{\sigma ^2}} \right)\]

表示。

给出数据，且已知数据 x 服从高斯分布（N(μ, σ²)）

\[\begin{array}{l}
\left\{ {{x^{\left( 1 \right)}},{x^{\left( 2 \right)}},...,{x^{\left( m \right)}}} \right\}\\
{x^{\left( 1 \right)}} \in
\end{array}\]

用如下公式分别确定 μ，和 σ²

\[\begin{array}{l}
\mu = \frac{1}{m}\sum\limits_{i = 1}^n {{x^{\left( i \right)}}} \\
{\sigma ^2} = \frac{1}{m}\sum\limits_{i = 1}^m {{{\left( {{x^{\left( i \right)}} - \mu } \right)}^2}}
\end{array}\]

注意：数学中确定 σ 会用 m-1 作为分母，但是在机器学习中通常用 m 作为分母，由于数据量很大，所以影响不大。

---

有如下数据集

\[\begin{array}{l}
\left\{ {{x^{\left( 1 \right)}},{x^{\left( 2 \right)}},...,{x^{\left( m \right)}}} \right\}\\
x \in {R^n}\\
{x^{\left( i \right)}} = \left( {x_1^{\left( i \right)},x_2^{\left( i \right)},...,x_n^{\left( i \right)}} \right)
\end{array}\]

假设数据的每个特征都服从高斯分布（如果不服从，看下面特征处理部分）

\[\begin{array}{l}
{x_1} \sim N\left( {{\mu _1},\sigma _1^2} \right)\\
{x_2} \sim N\left( {{\mu _2},\sigma _3^2} \right)\\
.\\
.\\
{x_n} \sim N\left( {{\mu _n},\sigma _n^2} \right)
\end{array}\]

则定义模型 p(x)

\[p\left( x \right) = p\left( {{x_1};{\mu _1},\sigma _1^2} \right)p\left( {{x_2};{\mu _2},\sigma _2^2} \right) \cdot  \cdot  \cdot p\left( {{x_n};{\mu _n},\sigma _n^2} \right)\]

或

\[p\left( x \right) = \prod\limits_{j = 1}^n {p\left( {{x_j};{\mu _j},\sigma _j^2} \right)} \]

这里假设每个因素是相互独立的（即使不独立这个模型也能很好的工作）

---

算法的流程

1，选择您认为可能表示异常示例的特征x

2，计算模型参数 μ₁, ...., μ_n, σ₁², ..., σ_n²

\[\begin{array}{l}
{\mu _j} = \frac{1}{m}\sum\limits_{i = 1}^n {x_j^{\left( i \right)}} \\
\sigma _j^2 = \frac{1}{m}\sum\limits_{i = 1}^m {{{\left( {x_j^{\left( i \right)} - {\mu _j}} \right)}^2}}
\end{array}\]

3，计算新数据的 p(x)

\[p\left( x \right) = \prod\limits_{j = 1}^n {p\left( {{x_j};{\mu _j},\sigma _j^2} \right)}  = \prod\limits_{j = 1}^n {\frac{1}{{\sqrt {2\pi } {\sigma _j}}}\exp \left( { - \frac{{{{\left( {{x_j} - {\mu _j}} \right)}^2}}}{{2\sigma _j^2}}} \right)} \]

4，如果 p(x) < ε 就定义为异常

---

如何评价异常检测结果？

虽然异常检测可以是无监督的，但是为了评估模型的性能，我们假设可以得到“有标签”的数据

举例

对于飞机引擎的例子，如果有

• 10000 好的引擎样本
• 20 个以尝引擎样本

可以将数据做如下分类

• 训练集：6000 个好的引擎（y=0）
• 交叉验证集：2000 个好的引擎（y=0），10 个异常的引擎（y=1）
• 测试集：2000 个好的引擎（y=0），10 个异常的引擎（y=1）

然后，运用训练集去训练模型得到 p(x)

接着用交叉验证集去测试模型准确率

\[y = \left\{ {\begin{array}{*{20}{c}}
{\begin{array}{*{20}{c}}
1&{p(x) < \varepsilon \left( {anomaly} \right)}
\end{array}}\\
{\begin{array}{*{20}{c}}
0&{p(x) \ge \varepsilon \left( {nomal...} \right)}
\end{array}}
\end{array}} \right.\]

这里有几个评价指标

• True positive, false positive, false negative, true negative
• Precision/Recall
• F₁-score

交叉验证集的作用

• 根据这些评价指标的结果可以调整 ε 的大小
• 根据这些评价指标的结果可以调整选取的表征引擎状态的特征

最后，将最终模型运用在测试集上

---

既然有了标签，为什么不用监督学习？

Anomaly detection	Supervised learning
Very small number of positive  examples (y = 1). (0-20 is common)	Large number of positive and negative examples.
Large number of negative (y = 0) examples.
Many different "type" of anomalies. Hard of any algorithm to learn from positive examples what the anomalies look like;	Enough positive examples for algorithm to get a sense of what positive examples are like, future positive examples likely to be  similar to ones in training set.
future anomalies may look nothing like any of the anomalous examples we've seen so far.

 

总结：

异常数据特点

• 异常检测通常只有很少的正样本（y = 1），但是有很多的负样本；
• 正样本“类型”差异度大，这就导致任何算法都很难从这些差异较大的正样本中学到“信息”；
• 将来出现的正样本有有很大可能与已有的正样本没有任何“相似度”。

其实上面的种种特点已经表明，监督学习算法很难适应上述数据特点：

• 监督学习需要大量的正样本与负样本来建立模型，这样它才能知道“正样本长得想什么”，“负样本长的像什么”；
• 监督学习对预测样本的要求是：将来的正负样本与训练集中的样本具有一定的相似度。

因此，对于异常数据，选用异常检测模型。

---

如何选择特征

选择那些：当异常事件发生时，特征的值非常大或者非常小的特征。

---

 

特征处理

上面假设数据的特征服从某种高斯分布

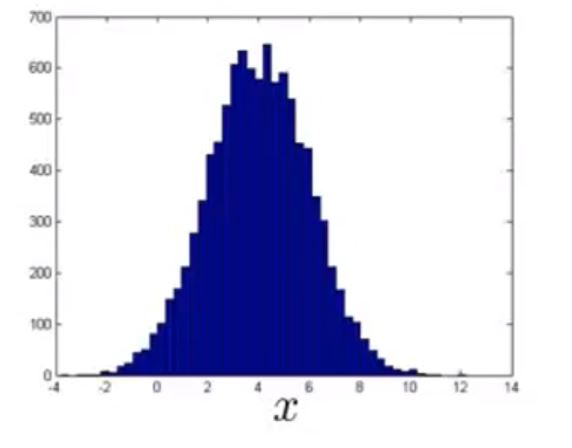
如果服从最好，如果不服从，而是像这样

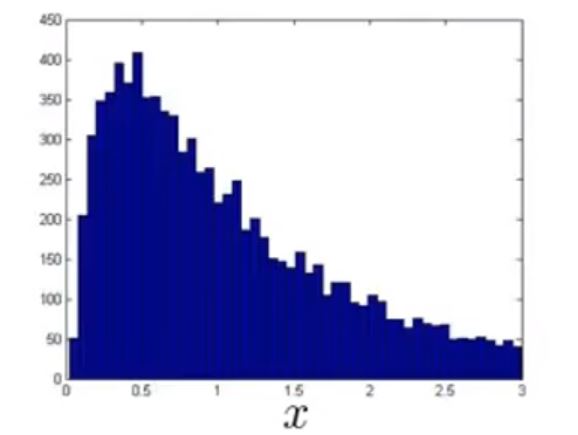
这种情况下，虽然算法也能较好的运行，但是一般情况下会将数据进行处理，比如将 x 替换为 log(x)

\[x \leftarrow \log \left( x \right)\]

数据分布就更像高斯分布了。

同理，也可以使用别的表达式来处理原始特征，使其更接近高斯分布

\[\begin{array}{l}
x \leftarrow \log \left( {x + c} \right)\\
x \leftarrow {x^c}
\end{array}\]

---

异常检测的误差分析

我们希望得到的情况是：

• 对于正常数据，希望得到的 p(x) 尽可能大
• 对于异常数据，希望得到的 p(x) 尽可能小

但是，通常情况下，你会发现，正常数据异常数据得到的 p(x) 都很大，该怎么办？

比如，当你发现在某个特征中得到较大 p(x₁) 的数据是一个异常点

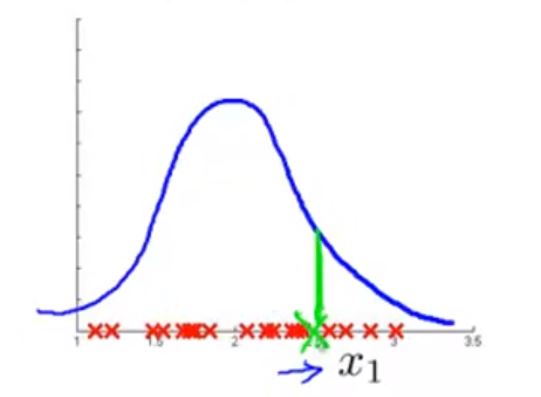
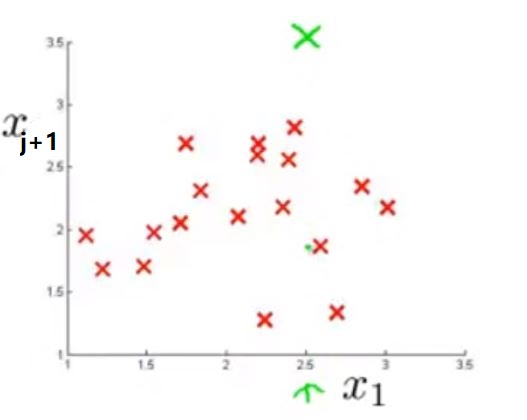
这时，你可以建立一个新的特征，比如 xj+1 来使得 p(x₁)p(x_j+1) 很小，这样得到的最终 p(x) 就会比较小，从而符合我们的要求。

---

运用多元高斯分布做异常检测

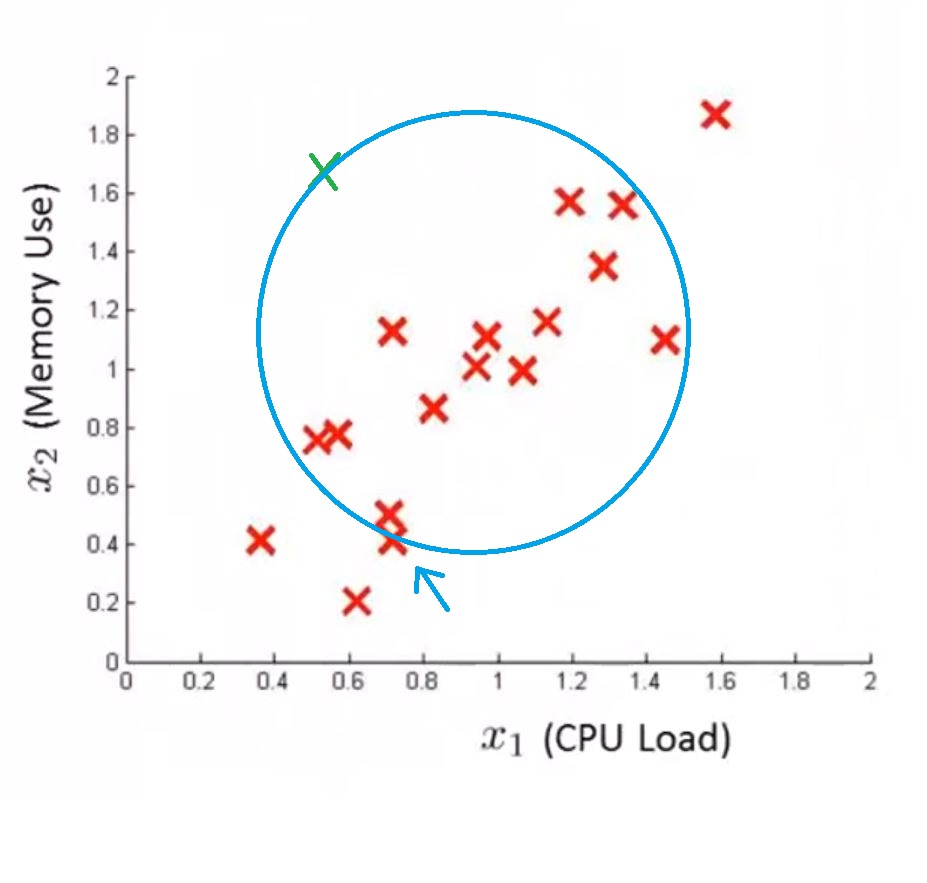
对于如下数据

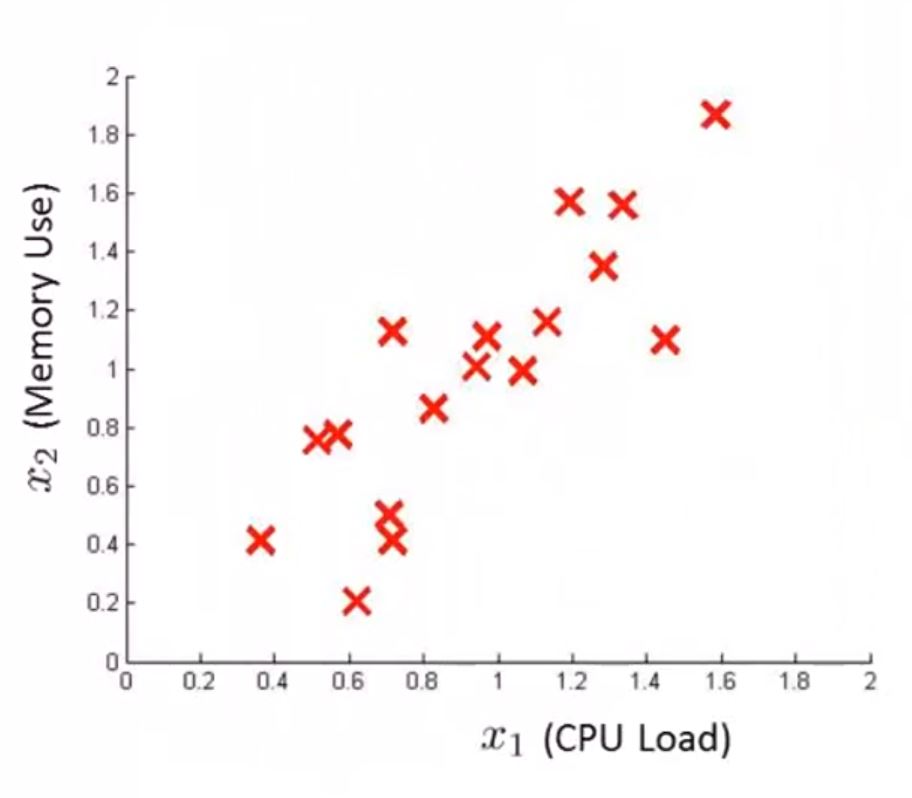
假如 x₁, x₂ 服从如下分布

对于如下数据点，可以看出它应该属于异常点

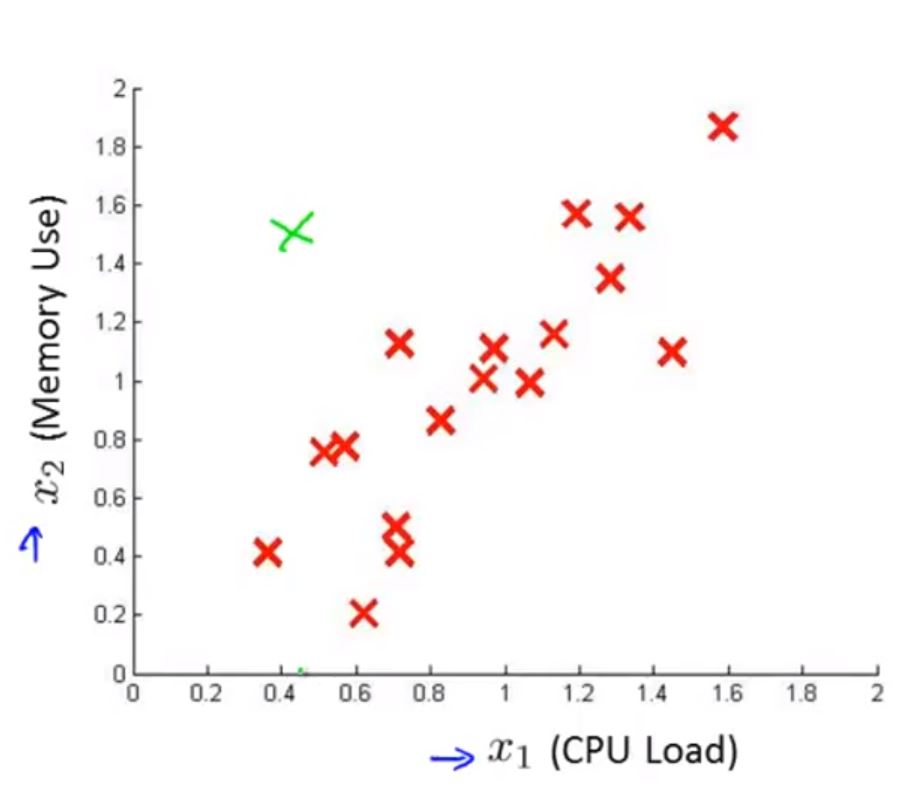
但是，对于常规的运用高斯分布的异常检测模型来说，它得到的 p(x) 与箭头所指数据得到的 p(x) 是一样的，这是不合理的。

多元高斯分布

在多元高斯分布的异常检测模型中，我们不再分别单独使用 p(x1), p(x2),...，而是将它们整合到一起。这里有参数

\[\mu  \in {R^n},\sum  \in {R^{nxn}}\]

μ 是各个特征的均值组成的 n 维向量，Σ 是 n x n 的协方差矩阵

定义模型为

\[p\left( {x;\mu ,\sum } \right) = \frac{1}{{{{\left( {2\pi } \right)}^{\frac{n}{2}}}{{\left| \sum  \right|}^{\frac{1}{2}}}}}\exp \left( { - \frac{1}{2}{{\left( {x - \mu } \right)}^T}{\sum ^{ - 1}}\left( {x - \mu } \right)} \right)\]

|Σ| 表示矩阵的行列式

接下来给出不同 μ 与 Σ 情况下的图形

可以看到 Σ 取不同值时 p(x) 的大小和变化趋势的变化

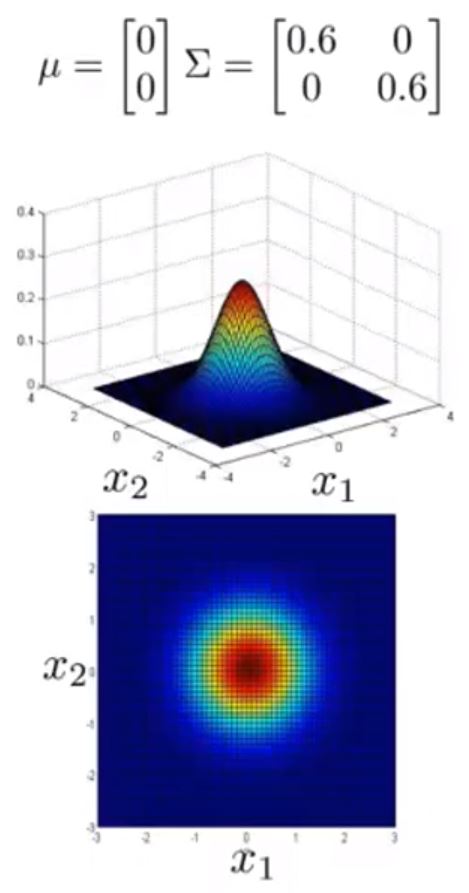
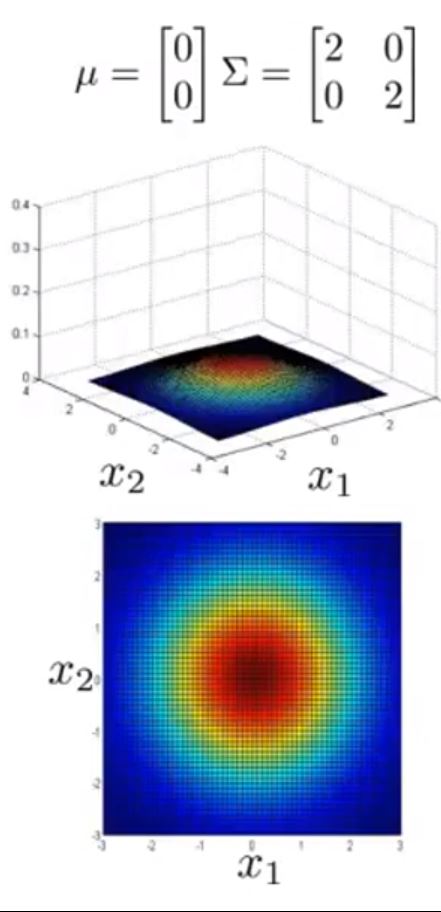
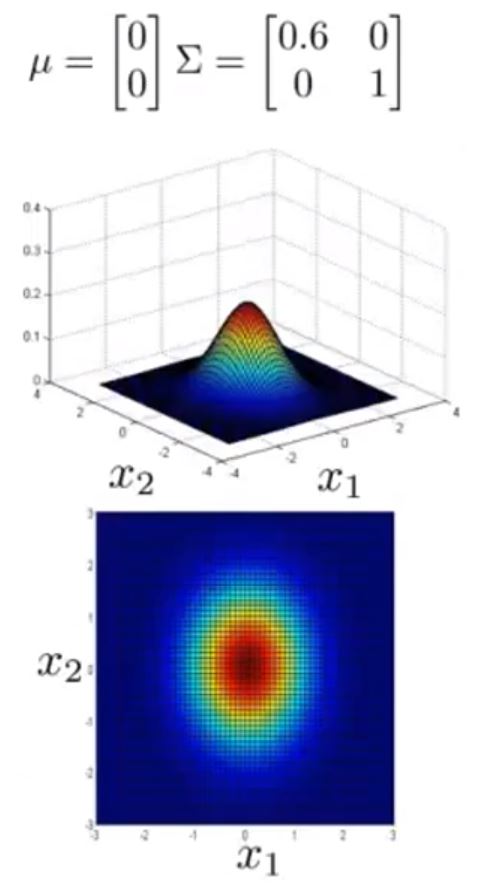
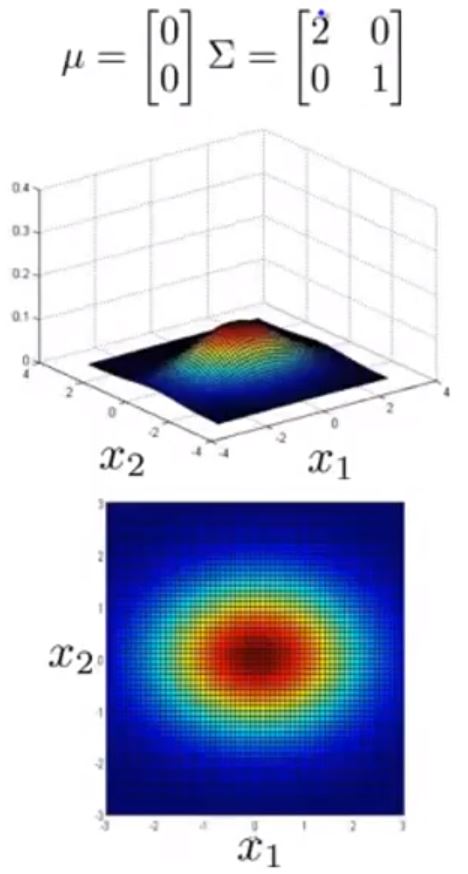
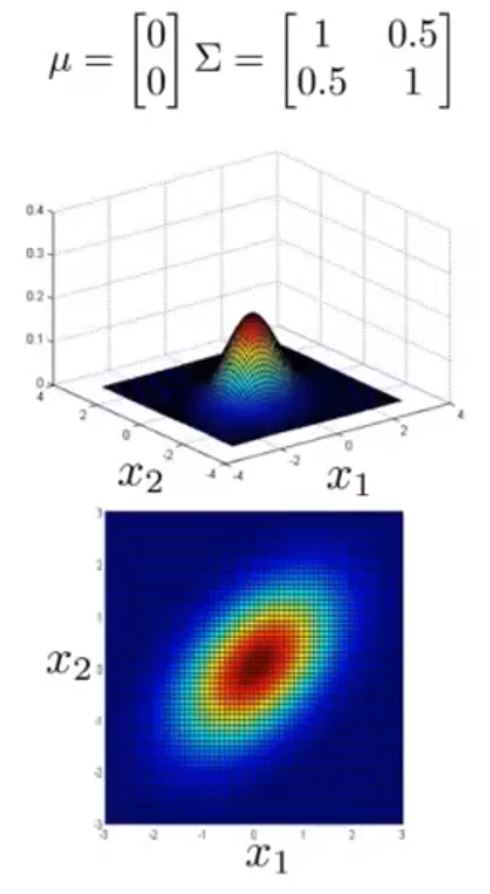
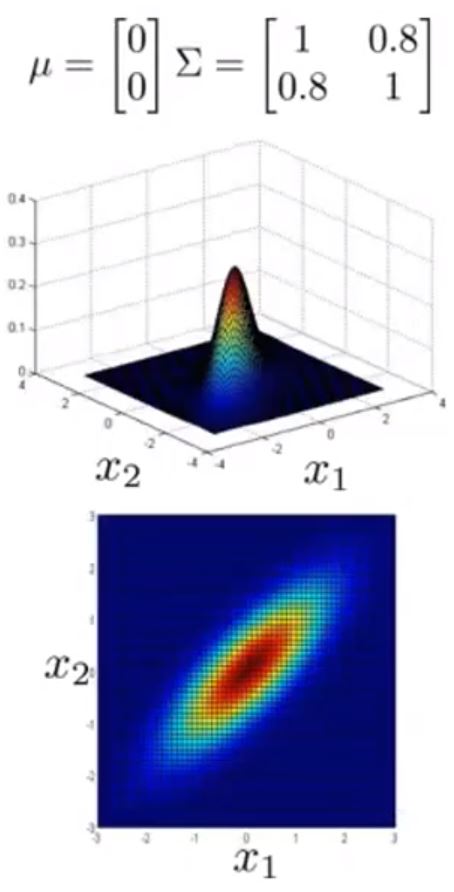
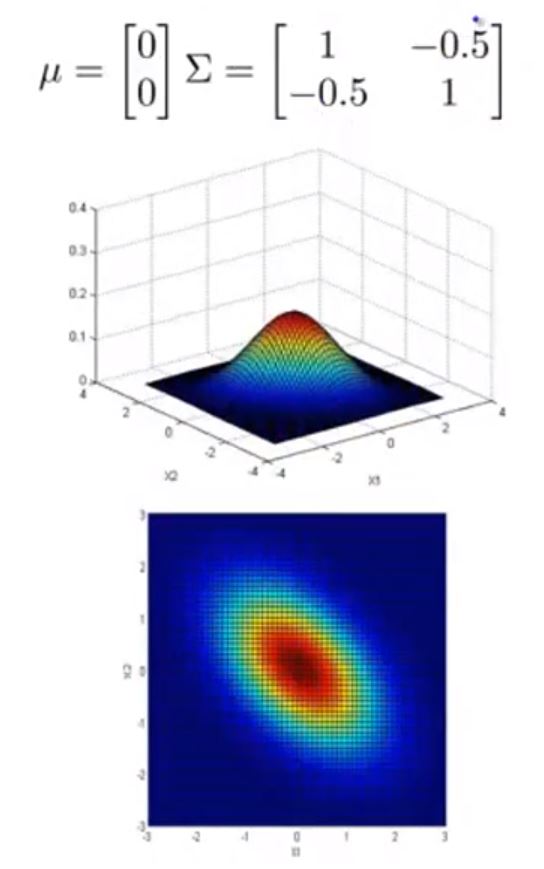
以及 μ 变化时，图形的变化趋势

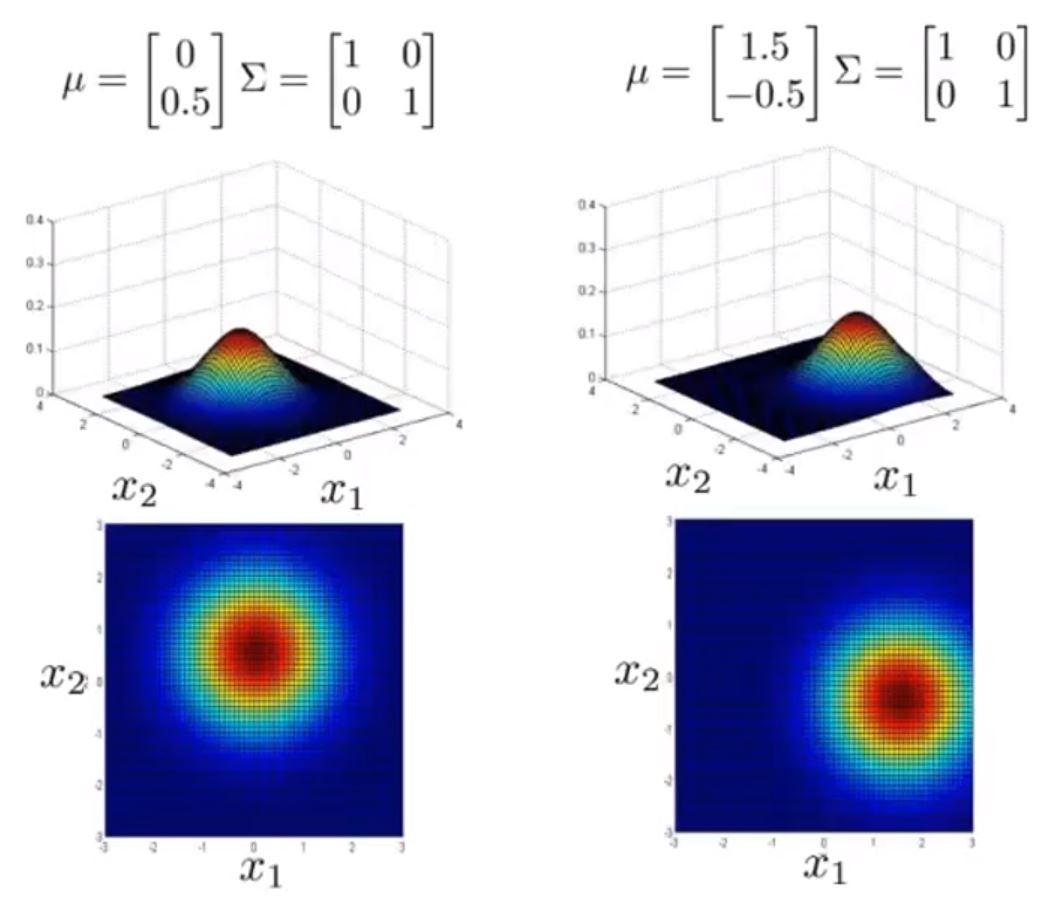
这样，图形就能很好的适应前面提到的常规高斯分布的异常检测模型难以解决的问题了。

 如何确定 参数 μ 和参数 Σ ？

假设训练集为

\[\left\{ {{x^{\left( 1 \right)}},{x^{\left( 2 \right)}},...,{x^{\left( m \right)}}} \right\}\]

则

\[\begin{array}{l}
\mu = \frac{1}{m}\sum\limits_{i = 1}^n {{x^{\left( i \right)}}} \\
\sum = \frac{1}{m}\sum\limits_{i = 1}^m {\left( {{x^{\left( i \right)}} - \mu } \right){{\left( {{x^{\left( i \right)}} - \mu } \right)}^T}}
\end{array}\]

---

对比发现，传统高斯分布预测模型其实时多元高斯分布预测模型的一个特例，当

\[\sum = \left[ {\begin{array}{*{20}{c}}
{\sigma _1^2}&{}&{}&{}\\
{}&{\sigma _2^2}&{}&{}\\
{}&{}&.&{}\\
{}&{}&{}&{\sigma _1^2}
\end{array}} \right]\]

时，多元高斯分布模型就变成了传统高斯分布模型。

那么，什么时候用传统模型，什么时候用多元模型？

• 传统模型在处理“特征之间有关联”的情况时需要手动创建新的特征来避免关联，而多元模型可以自动解决关联问题；
• 传统模型的计算开销小于多元模型；
• 多元模型需要训练样本数量 m 大于特征数量 n ，否则 Σ 不可逆。而通常情况下只有当 m >> n （m > 10n）时，运用多元模型才是合适的。传统模型即使在训练集很小的情况下也能很好的工作。