无监督学习——K-means聚类

先用图来描述K-means怎么做的

对于如下数据

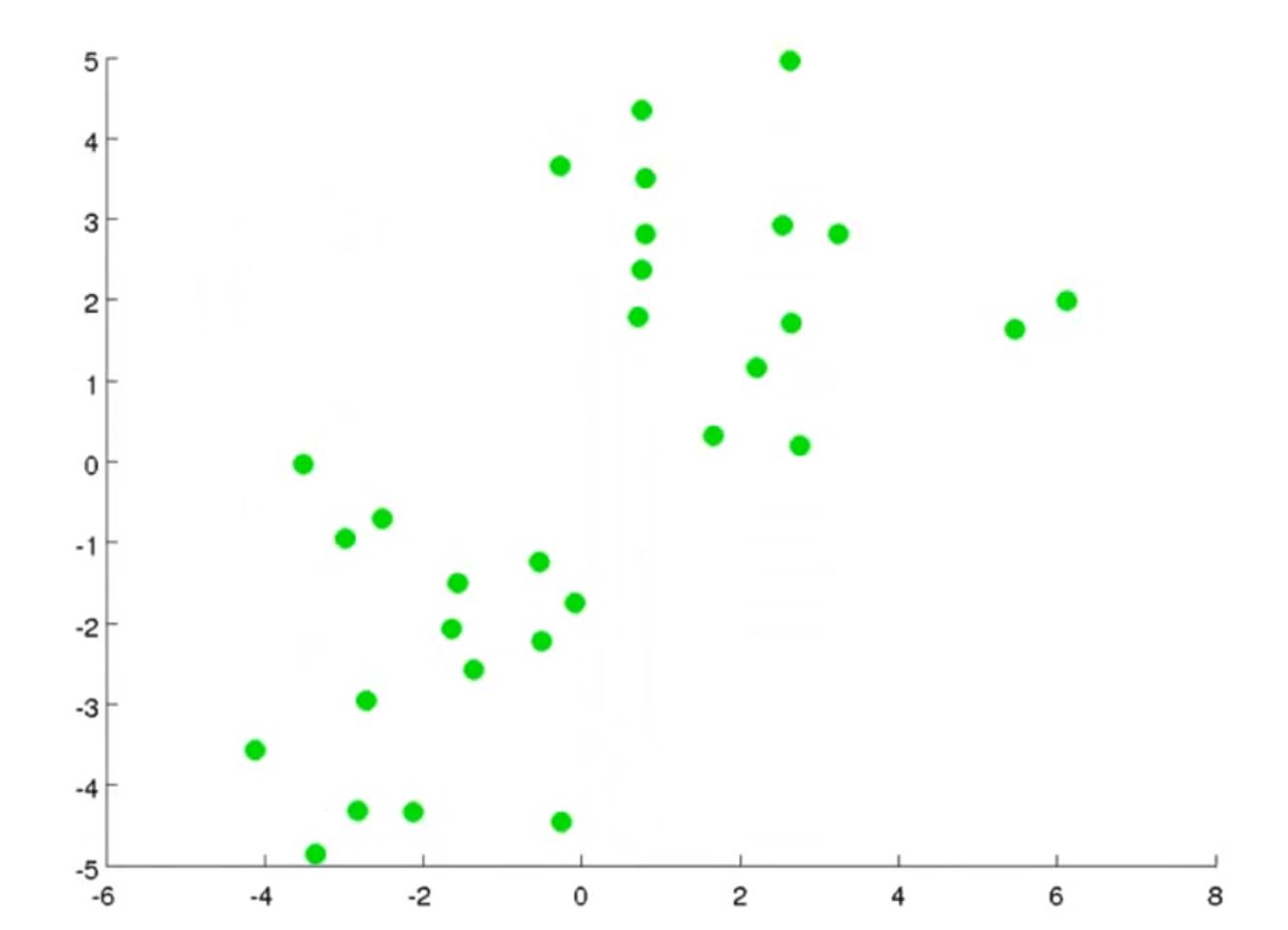
如果你想分成2类（k=2），算法会随机生成两个聚类中心

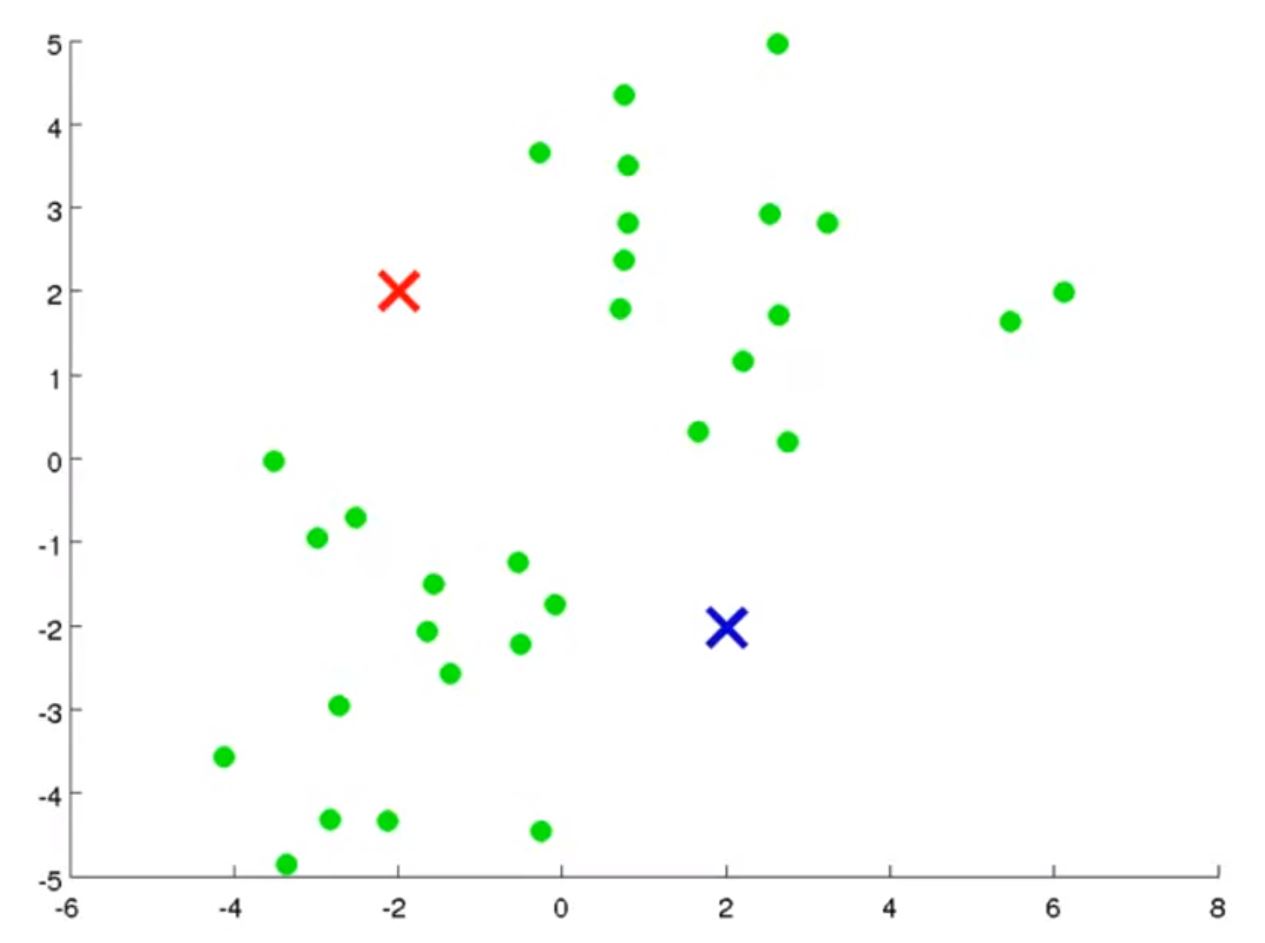
然后会分别计算每个数据（绿点）与聚类中心的距离（一般是欧式距离），来决定属于哪个类（距离哪个聚类中心近）

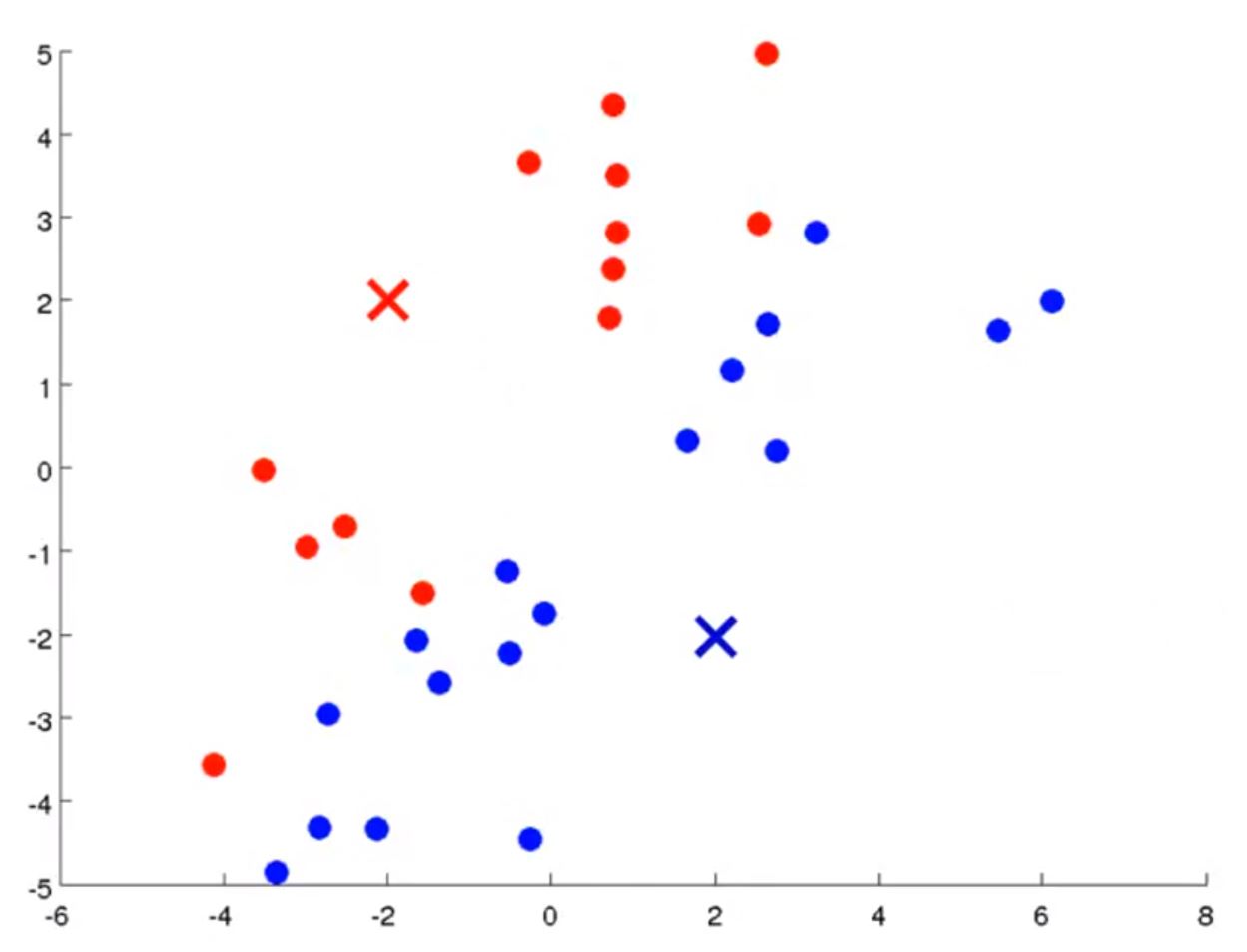
这样，就得到了数据的第一次分类，接下来算法会计算已分类的数据的“中心”，将它们作为新的聚类中心

这时，重新计算所有数据（红点和蓝点）与新的聚类中心的距离，并判断属于哪个类

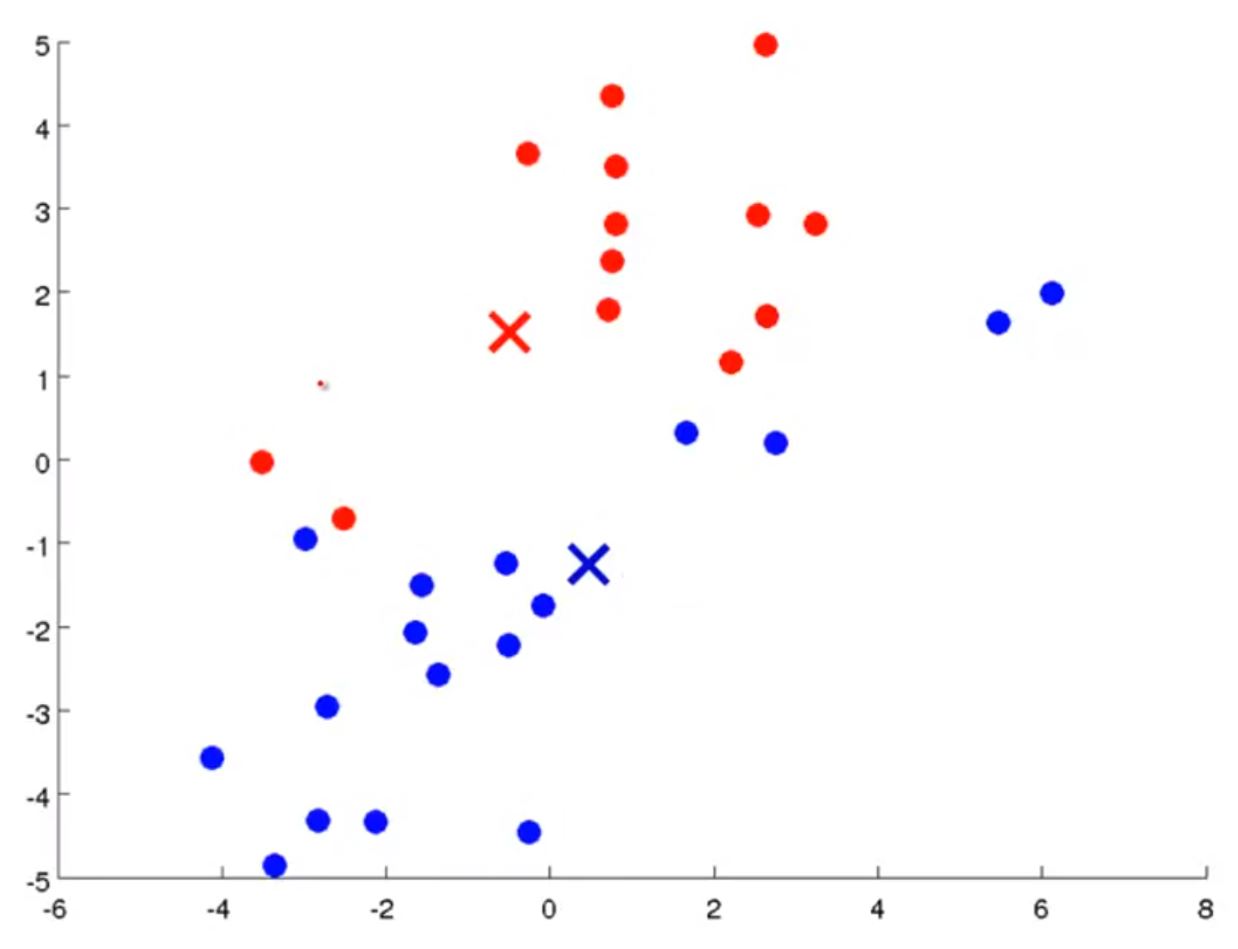
然后，重新计算新的分类的聚类中心

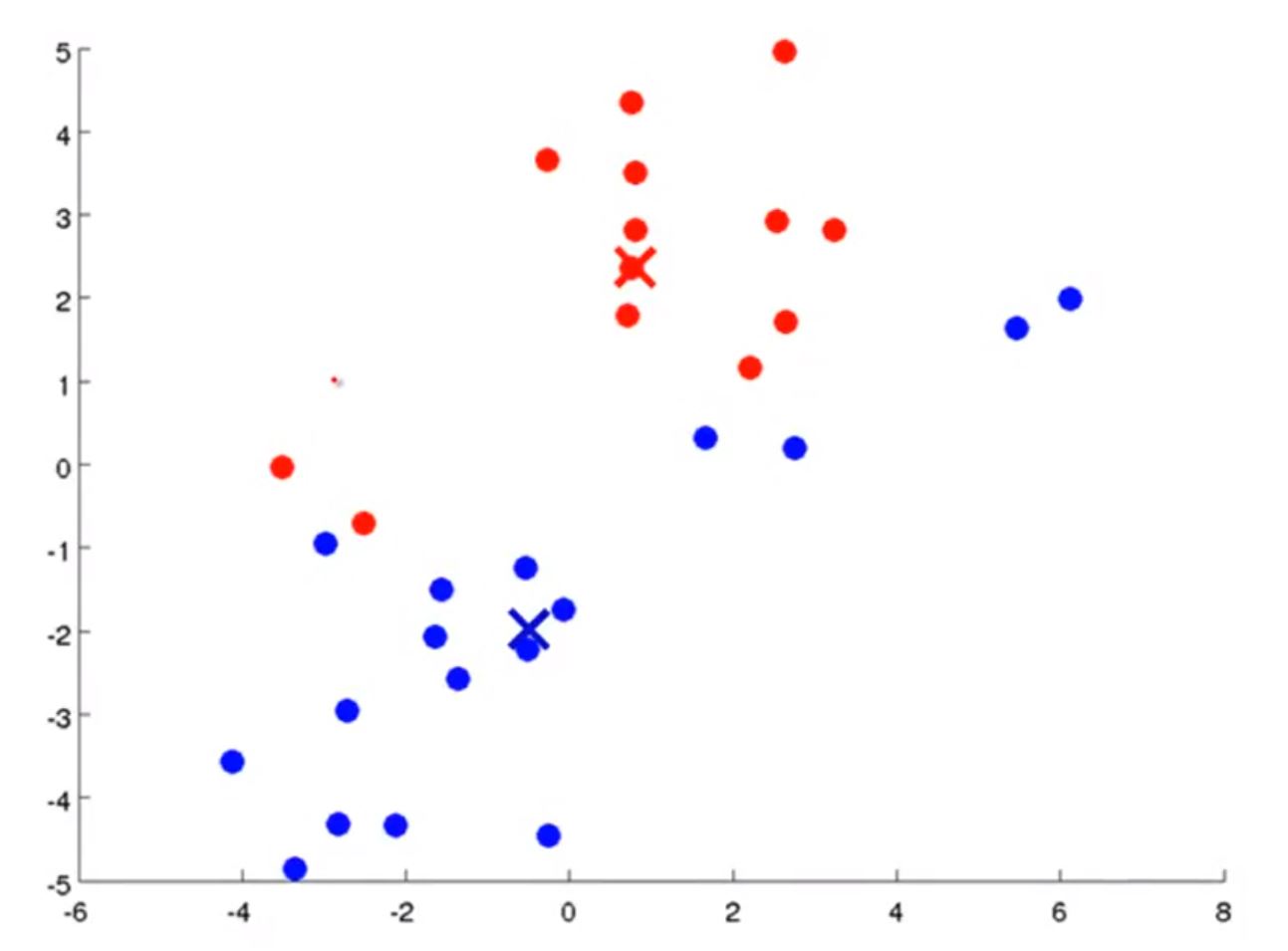
然后，重新计算数据点与新的聚类中心的距离，并决定属于哪个类

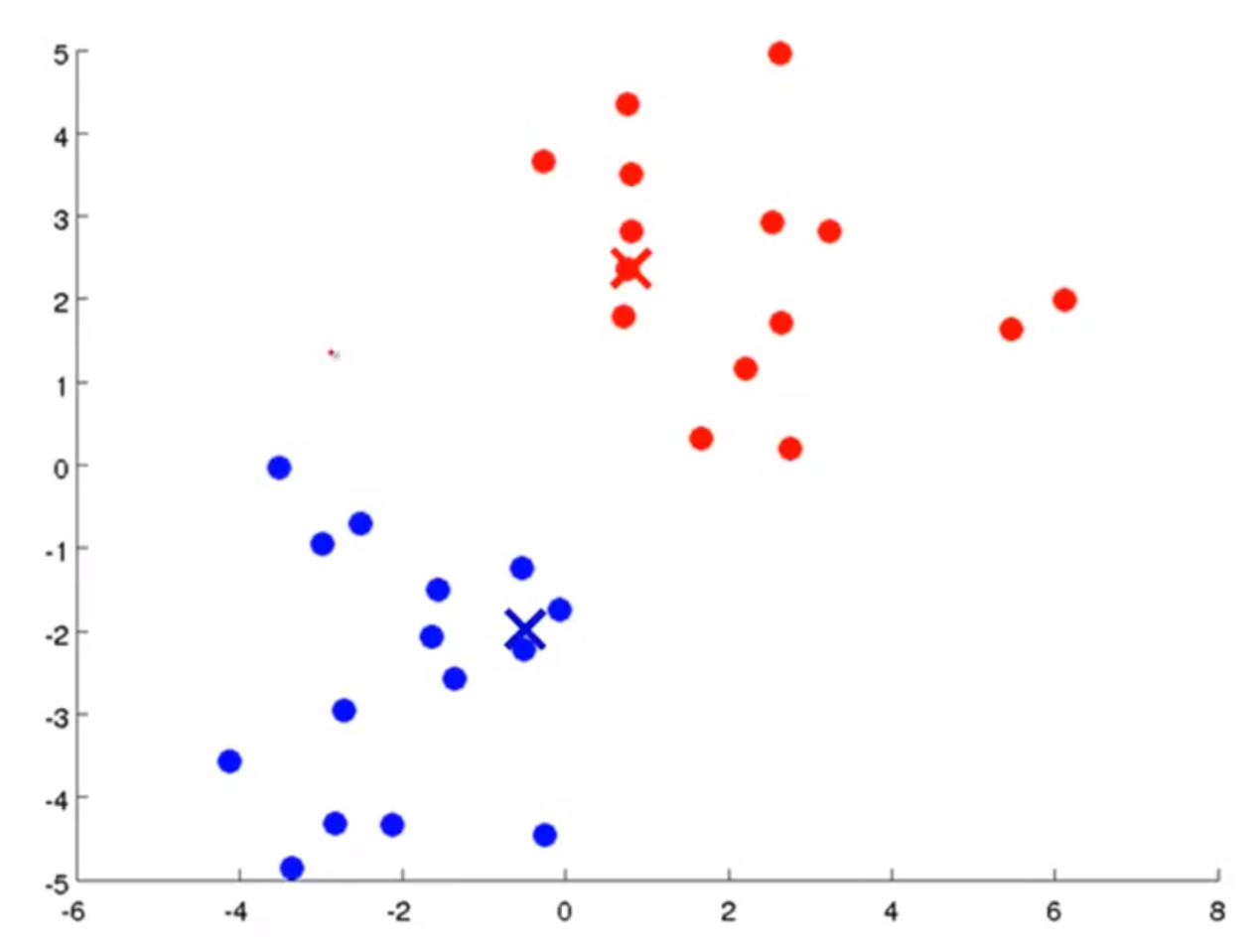
然后，重新计算聚类中心

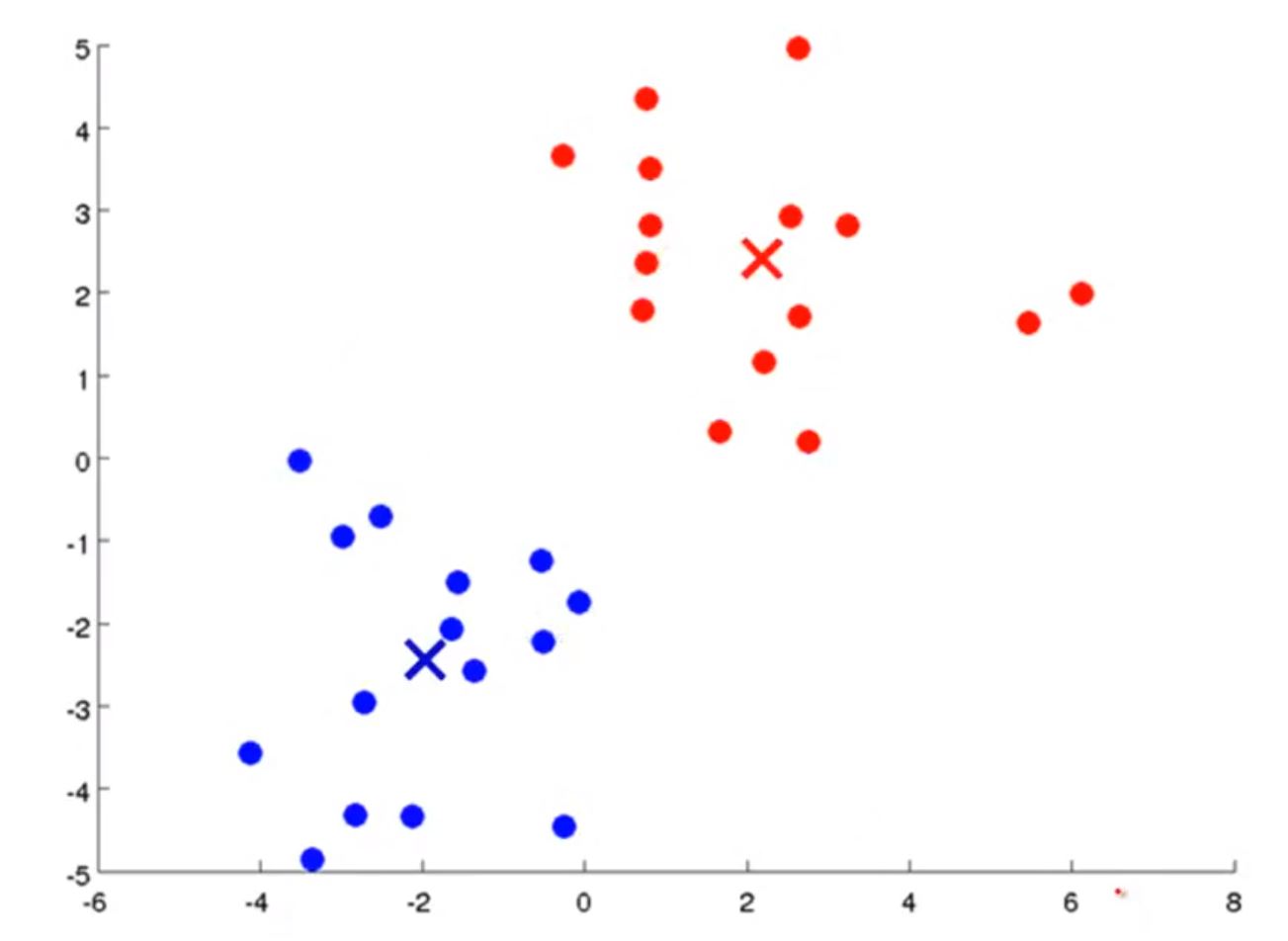
重点：就这样重复直到“新的聚类中心”与“上一次聚类中心”的位置相同，算法中止。

---

总结K-means算法

输入：

• K（聚类数）
• 训练样本

算法步骤：

随机选择K个“初始聚类中心”（μ₁, μ₂,..., μ_K）（每个聚类中心都是n维向量）

重复{

　　for i = 1 to m

　　　　c⁽ⁱ⁾ := 距离数据x(i)最近的中心

　　for k = 1 to K

　　　　μ_k := 所有属于类k的数据（第一步得到）的平均值

}

终止条件是聚类中心不再发生变化

---

K-means对于不可分数据的处理

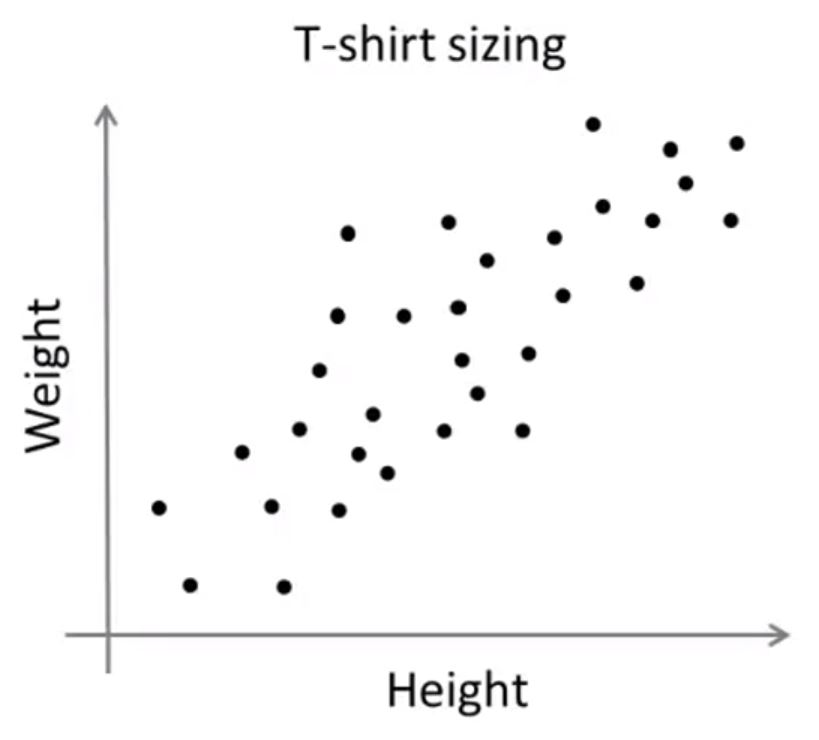
如果想要将衣服种类分为S, M, L三种类型，K-means最终得到的可能是

 

---

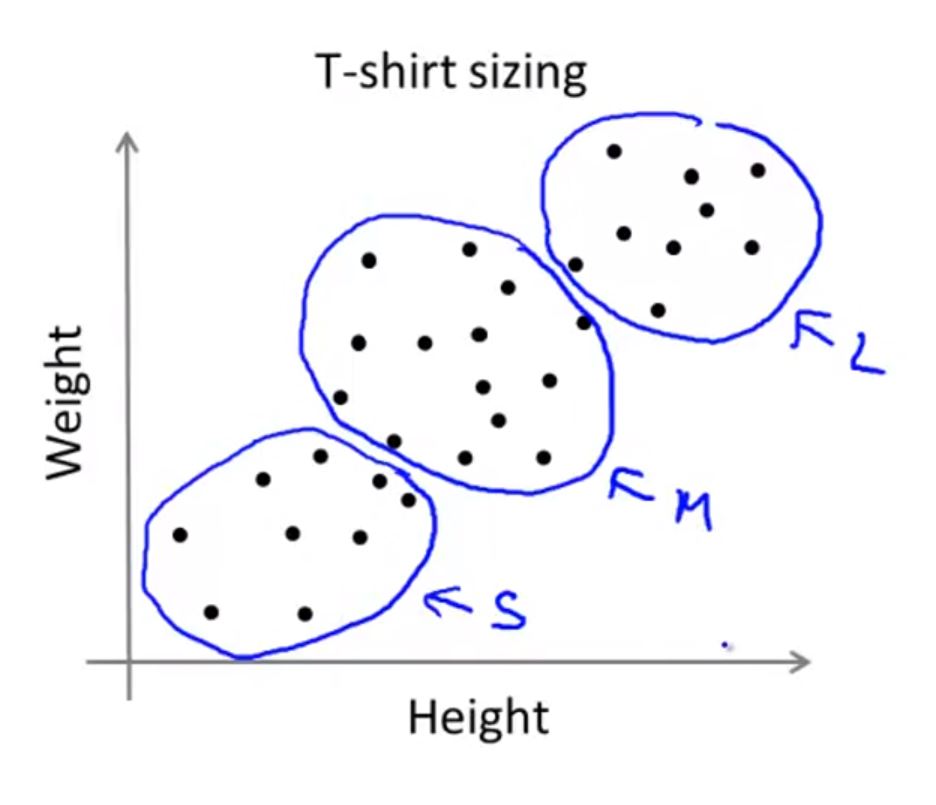
K-means的优化目标

符号：

• c⁽ⁱ⁾ := 表示样本x(i)当前所属的类
• μ_k = 第 k 个类别的中心
• μ_c⁽ⁱ⁾ = 样本x(i)所属类的聚类中心

则K-means的优化目标

\[\underbrace {\min }_{{c^{\left( 1 \right)}},...,{c^{\left( m \right)}},{\mu _1},...,{\mu _K}}J\left( {{c^{\left( 1 \right)}},...,{c^{\left( m \right)}},{\mu _1},...,{\mu _K}} \right) = \frac{1}{m}\sum\limits_{i = 1}^m {{{\left\| {{x^{\left( i \right)}} - {\mu _{{c^{\left( i \right)}}}}} \right\|}^2}} \]

意思是：最小化所有“数据与其所属类别中心距离的平均值”

我们可以用这个算是函数判断算法是否正常运行。

---

关于随机选取

首先，K < m

一种方法是随机选取K个样本作为“初始聚类中心”

注意：如果随机算则的初始聚类中心不当，就可能陷入局部最小。

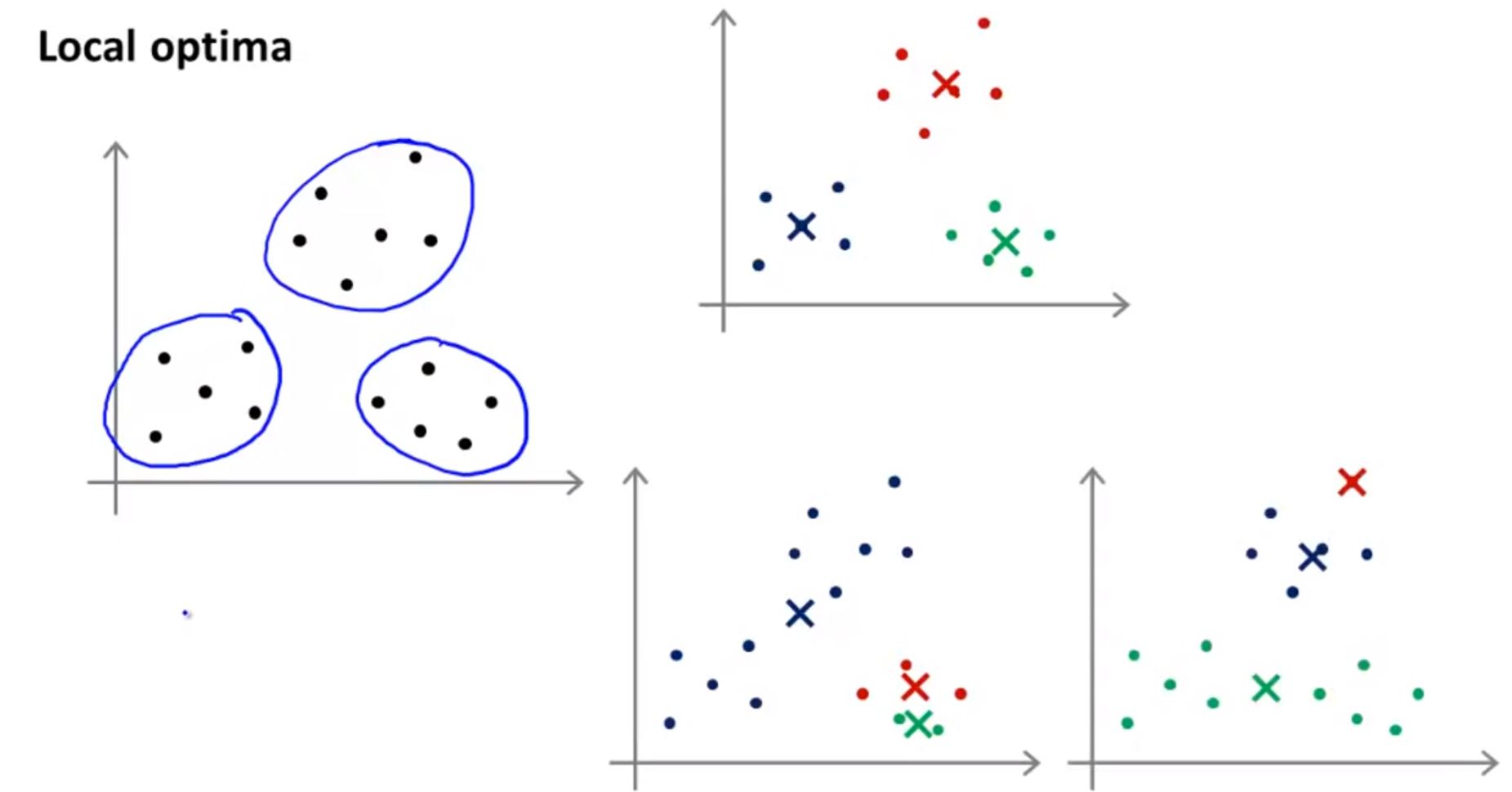
为了避免这种情况，可以尝试多次随机选取初始聚类中心的方法（比如50-1000次），然后选取其中“损失函数”最小的那个

---

如何选择K（聚类数）

一种方法是：“Elbow method”

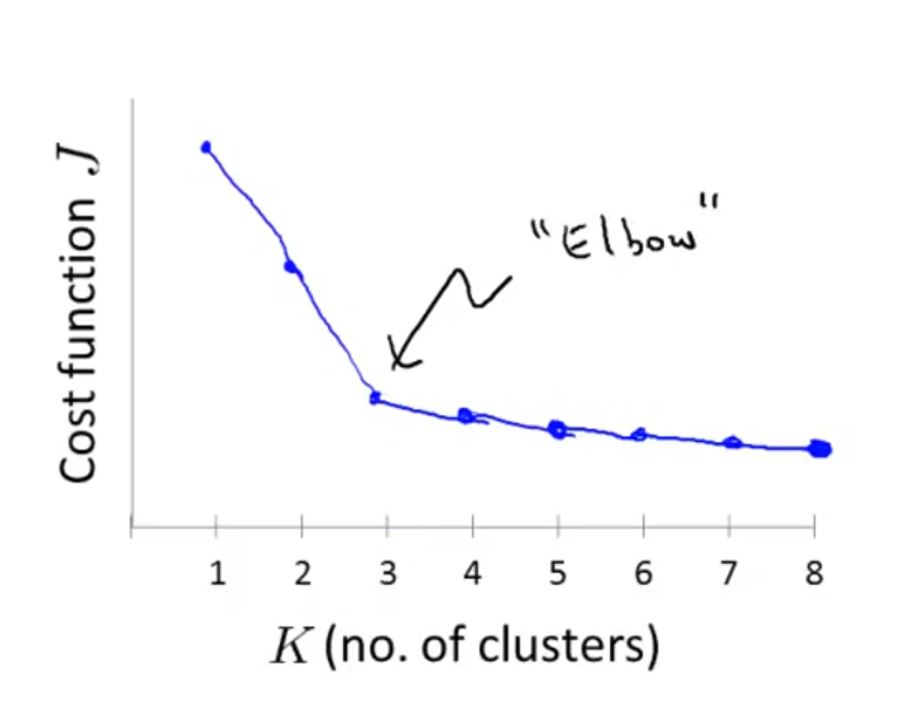
画出K-means的代价函数随K值变化的曲线，选择“elbow”所在位置的K（这里选择3）

但是这种方法很少用，因为，通常情况下得到的图会是如下情况，这样就很难作出判断

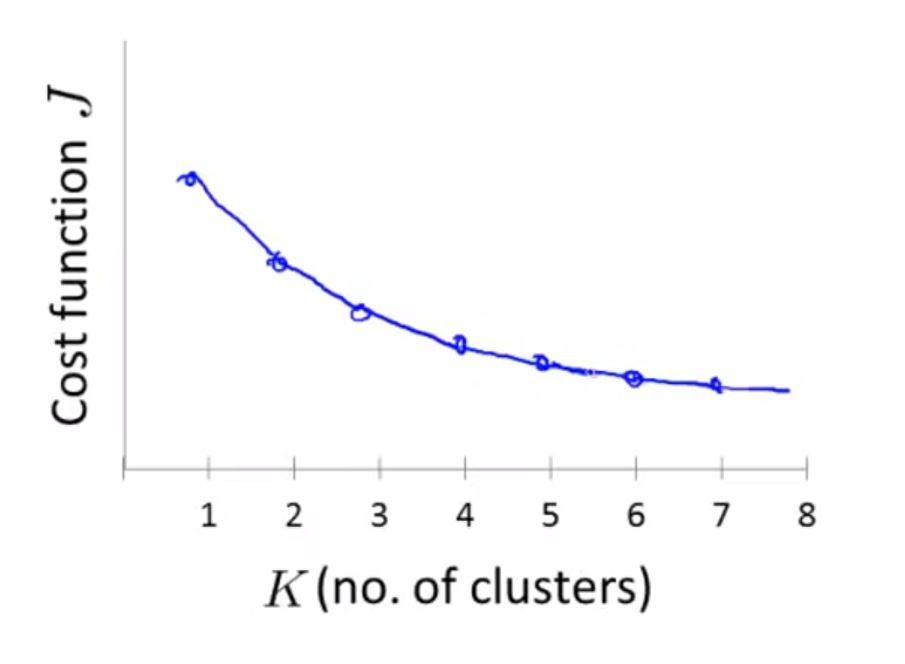
有些时候，你运用K-means方法聚类是为了之后的目的，而不是聚多少类在数学意义上最合理。（比如，衣服的尺码是分为3类还是5类，那就看那种分类卖得好，更符合市场需求）