支持向量机
逻辑回归的另一种观点
\[{h_\theta }\left( x \right) = \frac{1}{{1 + {e^{ - {\theta ^T}x}}}}\]
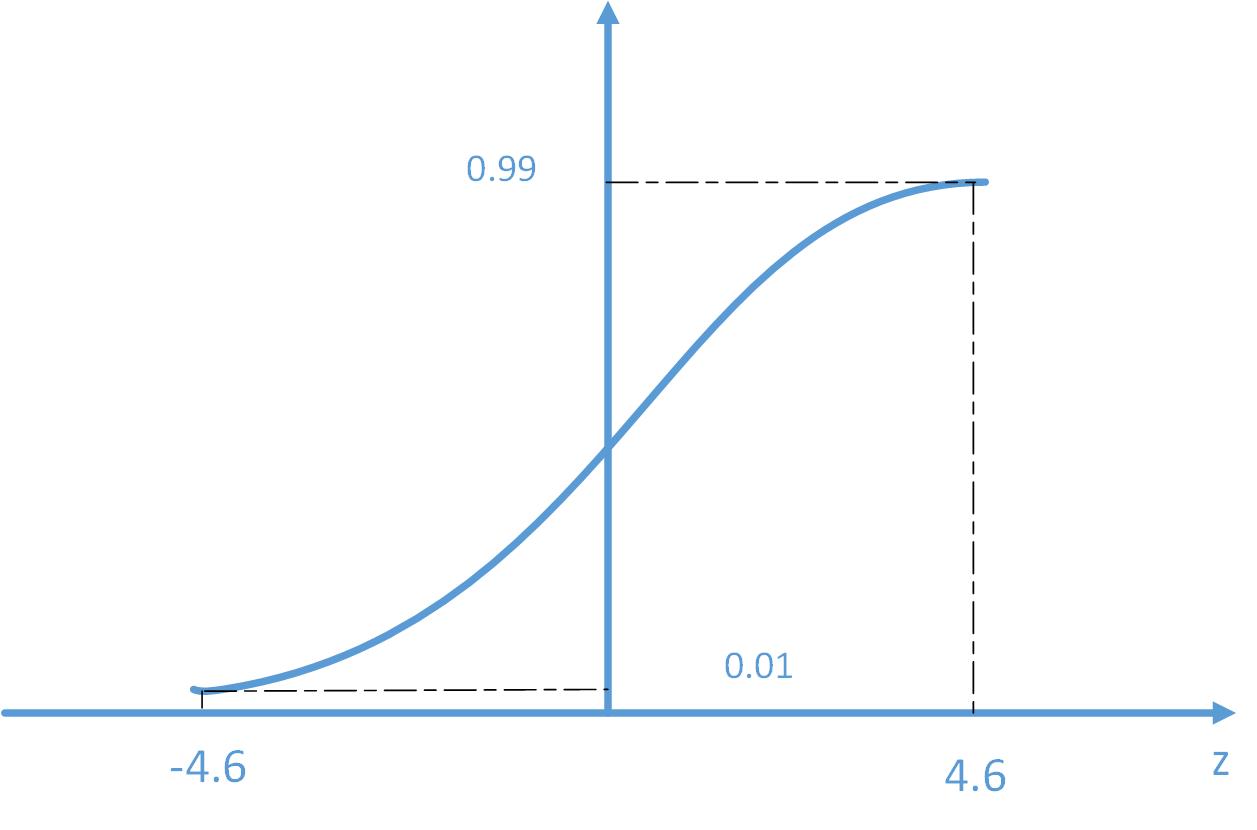
如果y=1,我们希望hθ(x)≈1,对应θTx >> 0
如果y=0,我们希望hθ(x)≈0,对应θTx << 0
对于一个样本(x, y)来说,它的损失函数为
\[\begin{array}{l}
- \left( {y\log \left( {{h_\theta }\left( x \right)} \right) + \left( {1 - y} \right)\log \left( {1 - {h_\theta }\left( x \right)} \right)} \right)\\
= - y\log \left( {\frac{1}{{1 + {e^{ - {\theta ^T}x}}}}} \right) - \left( {1 - y} \right)\log \left( {1 - \frac{1}{{1 + {e^{ - {\theta ^T}x}}}}} \right)
\end{array}\]
对于y=1的情况
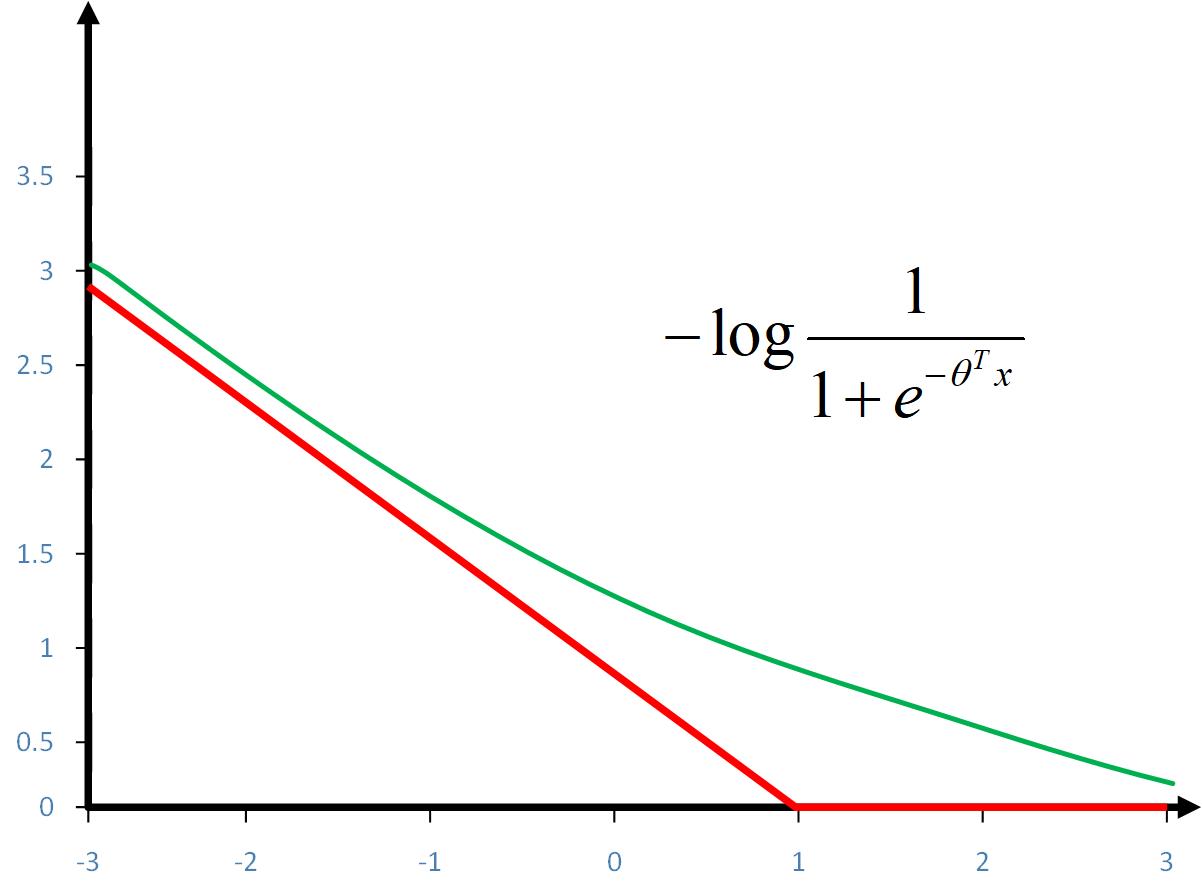
逻辑回归的损是函数变如图中绿线所示,损失函数变为
\[ - \log \left( {\frac{1}{{1 + {e^{ - z}}}}} \right)\]
支持向量机是将绿线替换成红线,称改变后的损失函数为
\[{\mathop{\rm Cos}\nolimits} {t_1}\left( z \right)\]
同理,当y=0时

逻辑回归的损是函数变如图中绿线所示,损失函数变为
\[ - \log \left( {1 - \frac{1}{{1 + {e^{ - z}}}}} \right)\]
支持向量机是将绿线替换成红线,称改变后的损失函数为
\[{\mathop{\rm Cos}\nolimits} {t_0}\left( z \right)\]
对于逻辑回归而言,它的目的是
\[\underbrace {\min }_\theta \left\{ {\frac{1}{m}\left[ {\sum\limits_{i = 1}^m {{y^{\left( i \right)}}\left( { - \log \left( {{h_\theta }\left( {{x^{\left( i \right)}}} \right)} \right)} \right) + \left( {1 - {y^{\left( i \right)}}} \right)\left( { - \log \left( {1 - {h_\theta }\left( {{x^{\left( i \right)}}} \right)} \right)} \right)} } \right] + \frac{\lambda }{{2m}}\sum\limits_{j = 1}^n {\theta _j^2} } \right\}\]
对于支持向量机而言,它将其中部分改变
\[\underbrace {\min }_\theta \left\{ {\frac{1}{m}\left[ {\sum\limits_{i = 1}^m {{y^{\left( i \right)}}{\mathop{\rm Cos}\nolimits} {t_1}\left( {{\theta ^T}{x^{\left( i \right)}}} \right) + \left( {1 - {y^{\left( i \right)}}} \right){\mathop{\rm Cos}\nolimits} {t_0}\left( {{\theta ^T}{x^{\left( i \right)}}} \right)} } \right] + \frac{\lambda }{{2m}}\sum\limits_{j = 1}^n {\theta _j^2} } \right\}\]
为方便起见,可以去掉1/m,这并不会影响θ的取值
\[\underbrace {\min }_\theta \left\{ {\left[ {\sum\limits_{i = 1}^m {{y^{\left( i \right)}}{\mathop{\rm Cos}\nolimits} {t_1}\left( {{\theta ^T}{x^{\left( i \right)}}} \right) + \left( {1 - {y^{\left( i \right)}}} \right){\mathop{\rm Cos}\nolimits} {t_0}\left( {{\theta ^T}{x^{\left( i \right)}}} \right)} } \right] + \frac{\lambda }{2}\sum\limits_{j = 1}^n {\theta _j^2} } \right\}\]
另一个改变是,去掉λ,在第一项前面乘上C
\[\underbrace {\min }_\theta \left\{ {C\left[ {\sum\limits_{i = 1}^m {{y^{\left( i \right)}}{\mathop{\rm Cos}\nolimits} {t_1}\left( {{\theta ^T}{x^{\left( i \right)}}} \right) + \left( {1 - {y^{\left( i \right)}}} \right){\mathop{\rm Cos}\nolimits} {t_0}\left( {{\theta ^T}{x^{\left( i \right)}}} \right)} } \right] + \frac{1}{2}\sum\limits_{j = 1}^n {\theta _j^2} } \right\}\]
为帮助理解,可以认为对于A+λB与(C)A+B两个式子,λ越大和C越小都可以表达“B的权重较大”这一概念。而且,当C=1/λ时,两个最小化式子返回同样的θ。
因此,支持向量机解决的问题是
\[\underbrace {\min }_\theta \left\{ {C\left[ {\sum\limits_{i = 1}^m {{y^{\left( i \right)}}{\mathop{\rm Cos}\nolimits} {t_1}\left( {{\theta ^T}{x^{\left( i \right)}}} \right) + \left( {1 - {y^{\left( i \right)}}} \right){\mathop{\rm Cos}\nolimits} {t_0}\left( {{\theta ^T}{x^{\left( i \right)}}} \right)} } \right] + \frac{1}{2}\sum\limits_{j = 1}^n {\theta _j^2} } \right\}\]
支持向量机的假设函数为
\[{h_\theta }\left( x \right) = \left\{ {\begin{array}{*{20}{c}}
{\begin{array}{*{20}{c}}
1&{{\theta ^T}x \ge 0}
\end{array}}\\
{\begin{array}{*{20}{c}}
0&{{\theta ^T}x < 0}
\end{array}}
\end{array}} \right.\]
以上就是支持向量机的数学定义。

