机器学习系统设计——误差矩阵

对于癌症检测的例子来说，y=1代表有癌症（1代表数目比较小的类）

Precision/Recall

		Actual	class
		1	0
Predicted	1	True positive	False Positive
class	0	False negative	True negative

\[\Pr ecision = \frac{{True \bullet positive}}{{predicted \bullet positive}} = \frac{{True \bullet positive}}{{True \bullet positive + Fake \bullet positive}}\]

 \[{\mathop{\rm Re}\nolimits} call = \frac{{True \bullet positive}}{{actual \bullet positive}} = \frac{{True \bullet positive}}{{True \bullet positive + Fake \bullet nagative}}\]

如果算法有“High precision”和“High recall”，我们就比较自信的认为这个算法是可以的。

---

在运用逻辑回归预测癌症的例子中

逻辑回归：0≤h_θ(x)≤1

预测为1：h_θ(x)≥0.5

预测为0：h_θ(x)<0.5

假设我们想在有癌症的情况下预测y=1

如何做到在非常自信（非常高的准确率）的情况下给出预测结果？

这时需要适当改变“threshold”

预测为1：h_θ(x)≥0.7

预测为0：h_θ(x)<0.7

这样做的结果你就会有“High precision”，但是会有“low recall”

“low recall”也是非常糟糕的情况，这种情况下你很可能会告诉一个有癌症的病人说他没有。。

这时需要适当改变“threshold”

预测为1：h_θ(x)≥0.3

预测为0：h_θ(x)<0.3

这样做的结果你就会有“High recall”，但是会有“low precision”，同样糟糕。。

---

可以画出不同“threshold”情况下的“precision”和“recall”

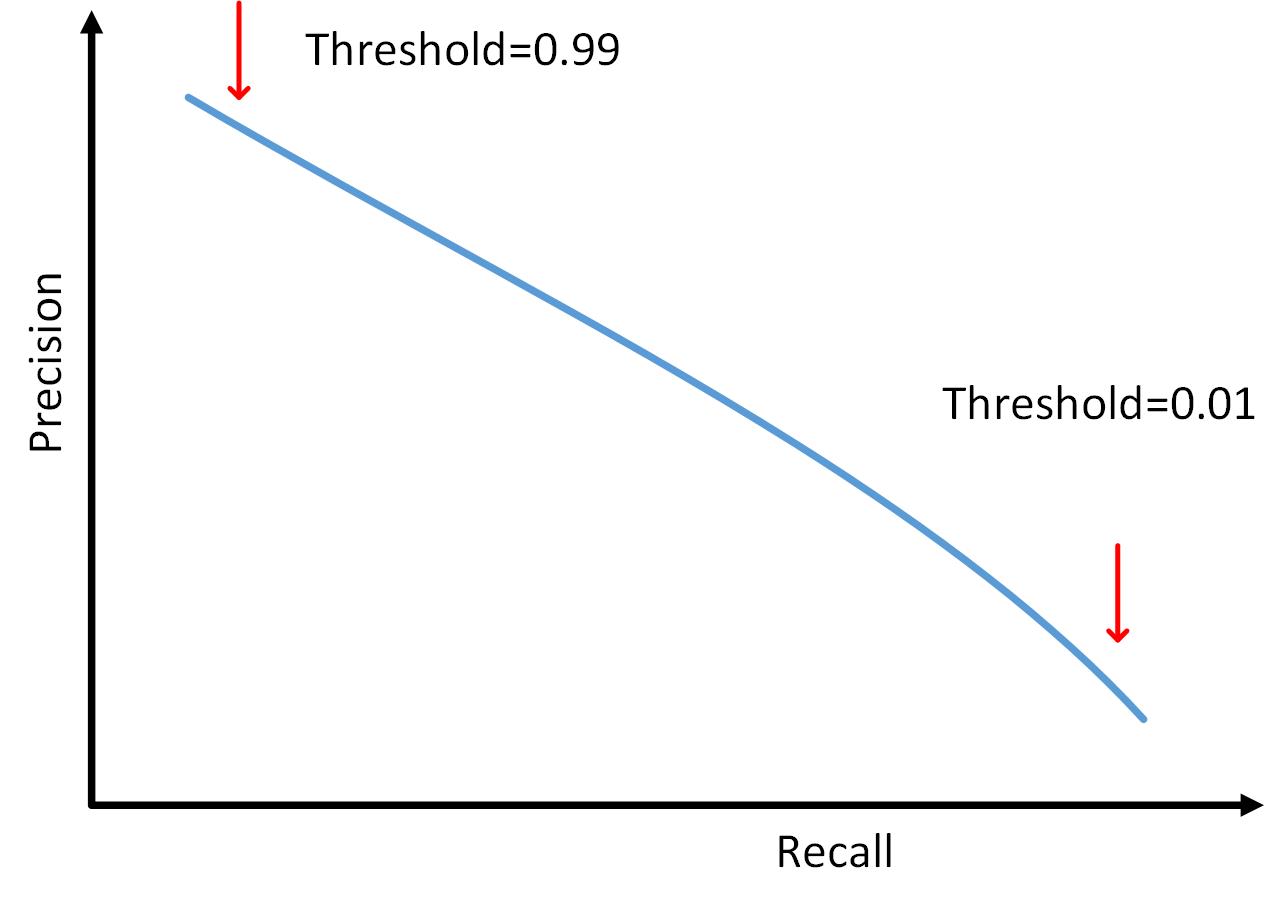
这样你可以根据需要选择“threshold”

---

如何根据“Precision”和“recall”选择算法？

现假设有不同算法的“Precision”和“recall”

 

	Precision(P)	Recall(R)	Average	F1Score
Algorithm 1	0.5	0.4	0.45	0.444
Algorithm 2	0.7	0.1	0.4	0.175
Algorithm 3	0.02	1.0	0.51	0.0392

一种方法是使用两者的平均值

\[A{\mathop{\rm var}} age:\frac{{P + R}}{2}\]

 这样做算法3会有比较高的得分，但是这样不太合理

一种是F₁Score

\[{F_1}Score:2\frac{{PR}}{{P + R}}\]

这是大多数人的用法

注意：这里的不同算法也可以是同一个算法取不同“threshold”时的情况。