梯度下降算法在线性回归中的运用
梯度下降算法
重复直到收敛{
\[{\theta _j}: = {\theta _j} - \alpha \frac{\partial }{{\partial {\theta _j}}}J\left( {{\theta _0},{\theta _1}} \right)\left( {for{\rm{ j = 0 and j = 1}}} \right)\]
}
线性回归模型{
\[{h_\theta }\left( x \right) = {\theta _0} + \theta_1 {x_1}\]
\[J\left( {{\theta _0},{\theta _1}} \right) = \frac{1}{{2m}}\sum\limits_{i = 1}^m {{{\left( {{h_\theta }\left( {{x^{(i)}}} \right) - {y^i}} \right)}^2}} \]
}
我们的目的是将梯度下降算法应用到线性回归中，最小化J(θ0, θ1)。
关键在于确定 \[\frac{\partial }{{\partial {\theta _{\rm{j}}}}}J\left( {{\theta _0},{\theta _1}} \right)\]
下面是推导过程
\[\begin{array}{l}
\frac{\partial }{{\partial {\theta _{\rm{j}}}}}J\left( {{\theta _0},{\theta _1}} \right) = \frac{\partial }{{\partial {\theta _{\rm{j}}}}}\frac{1}{{2m}}\sum\limits_1^m {{{\left( {{h_\theta }\left( {{x^{\left( i \right)}}} \right) - {y^{\left( i \right)}}} \right)}^2}} \\
= \frac{\partial }{{\partial {\theta _{\rm{j}}}}}\frac{1}{{2m}}\sum\limits_{i = 1}^m {{{\left( {{\theta _0} + {\theta _1}{x^{\left( i \right)}} - {y^{\left( i \right)}}} \right)}^2}}
\end{array}\]
当j=0时 \[\frac{\partial }{{\partial {\theta _0}}}J\left( {{\theta _0},{\theta _1}} \right) = \frac{1}{m}\sum\limits_{i = 1}^m {\left( {{h_\theta }\left( {{x^{\left( i \right)}}} \right) - {y^{\left( i \right)}}} \right)} \]
当j=1时 \[\frac{\partial }{{\partial {\theta _1}}}J\left( {{\theta _0},{\theta _1}} \right) = \frac{1}{m}\sum\limits_{i = 1}^m {\left( {{h_\theta }\left( {{x^{\left( i \right)}}} \right) - {y^{\left( i \right)}}} \right)} {x^{\left( i \right)}}\]
现在梯度下降算法就可以表示为
重复直到收敛{
\[\begin{array}{l}
{\theta _0}: = {\theta _0} - \alpha \frac{1}{m}\sum\limits_{i = 1}^m {\left( {{h_\theta }\left( {{x^{\left( i \right)}}} \right) - {y^{\left( i \right)}}} \right)} \\
{\theta _1}: = {\theta _1} - \alpha \frac{1}{m}\sum\limits_{i = 1}^m {\left( {{h_\theta }\left( {{x^{\left( i \right)}}} \right) - {y^{\left( i \right)}}} \right)} {x^{\left( i \right)}}
\end{array}\]
}
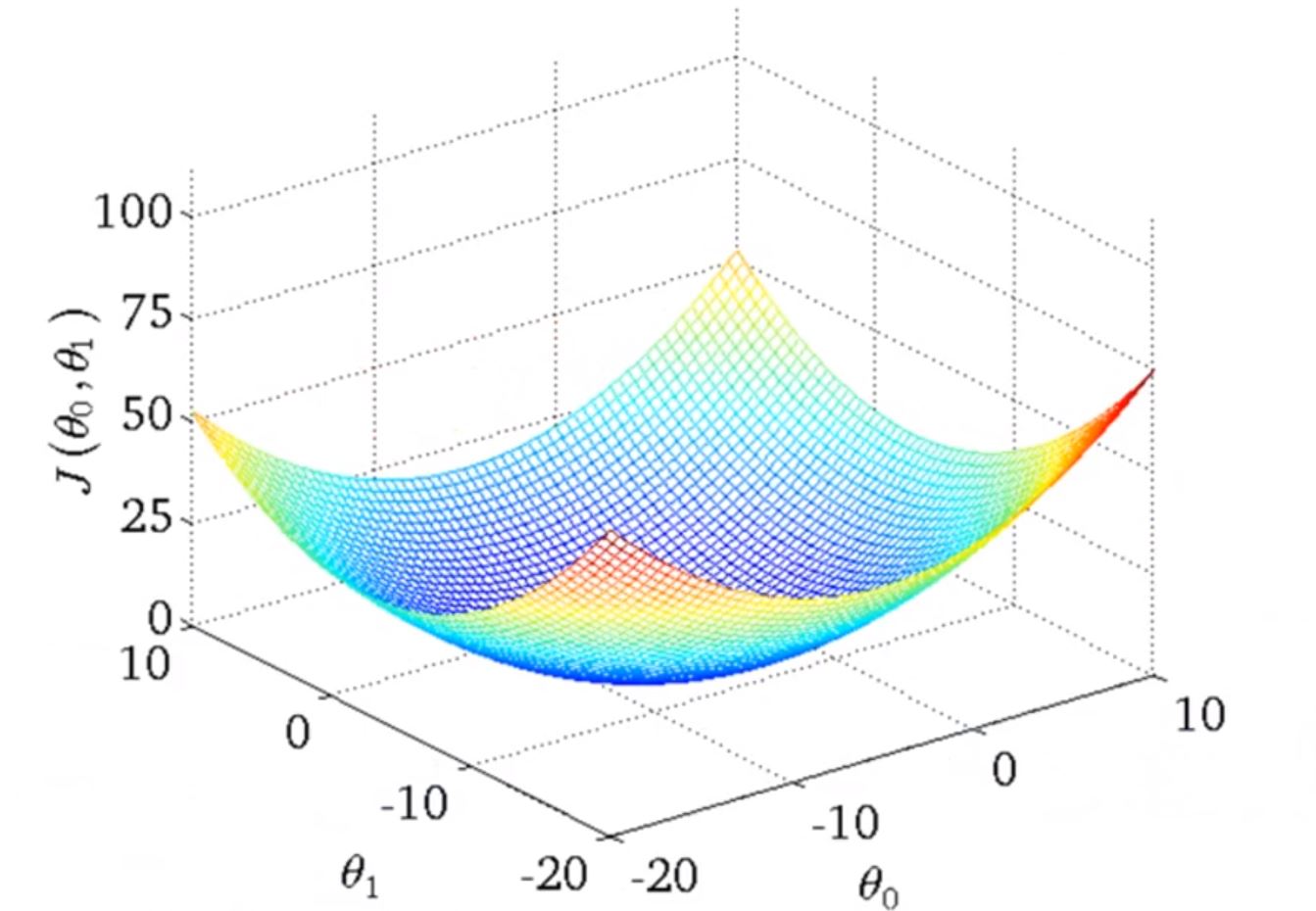
下面时梯度下降的示意图
梯度下降算法会根据不同初始点的选取陷入不同的局部最小。
但是就线性回归问题而言，它的代价函数的图形总是凸面函数（convex function）
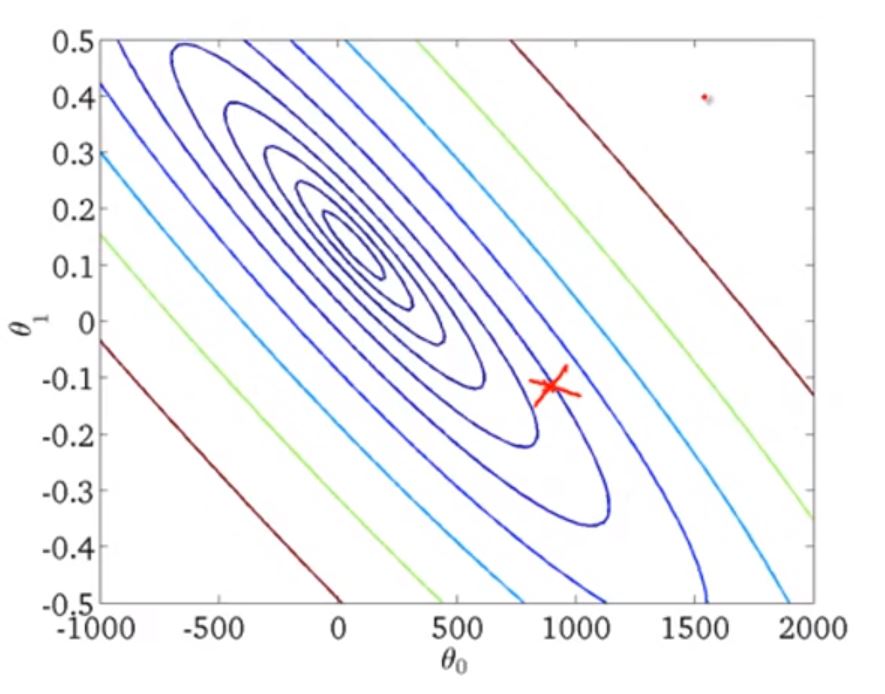
为方便起见，我们依然使用“等高线”图表示
假设初始点红叉所在位置，对应的h(θ)可能是右边的图
慢慢收敛到最佳的（θ0, θ1）
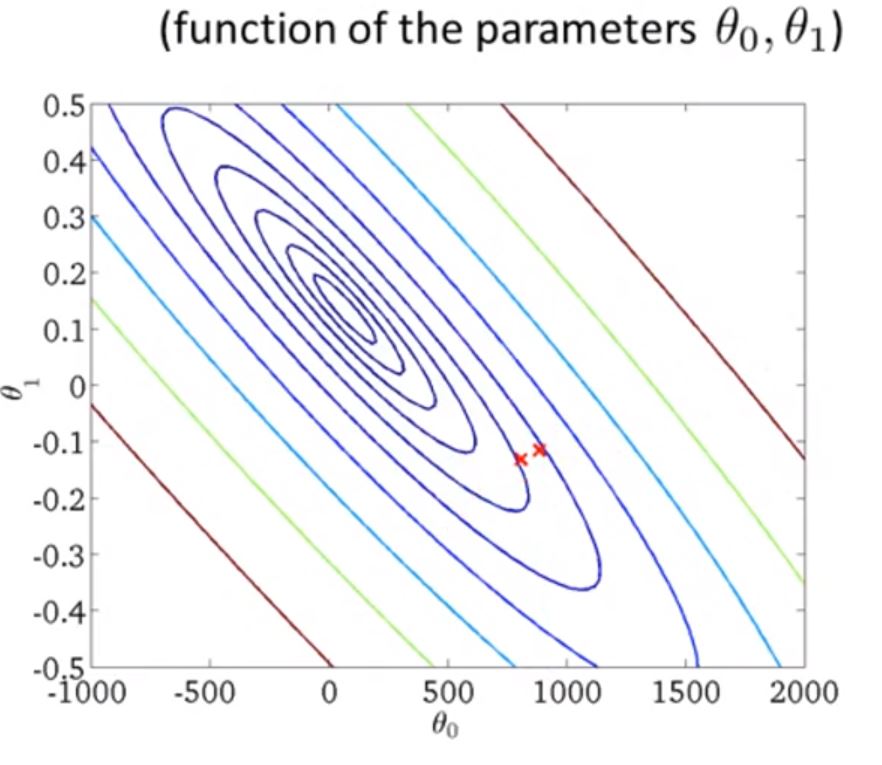
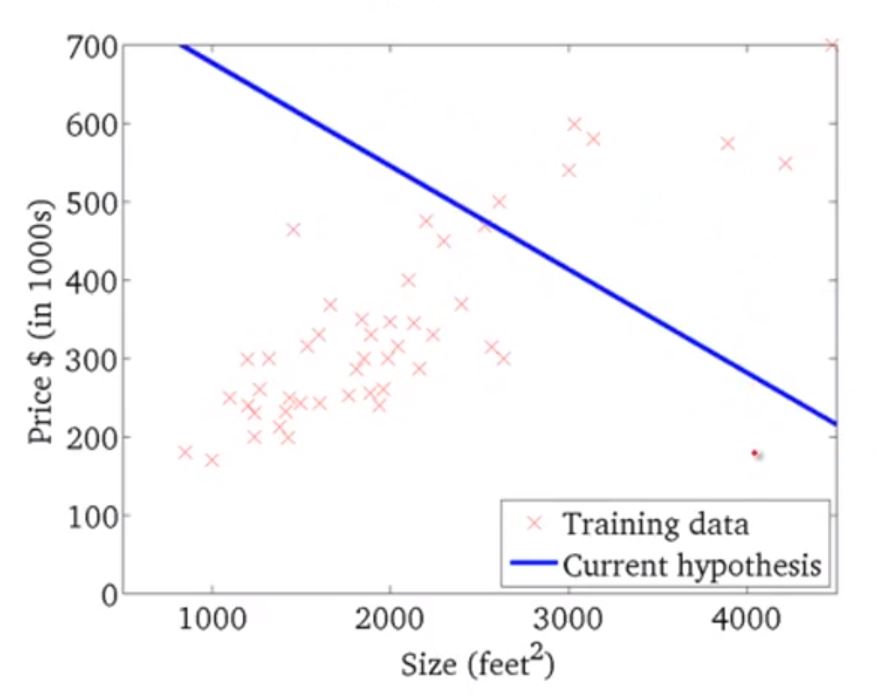
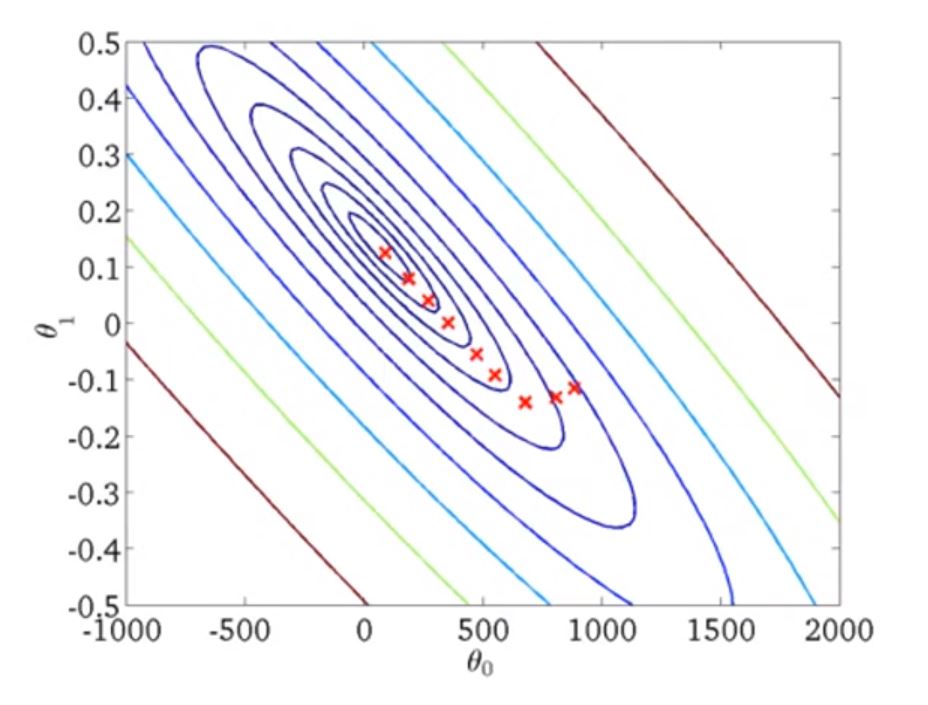
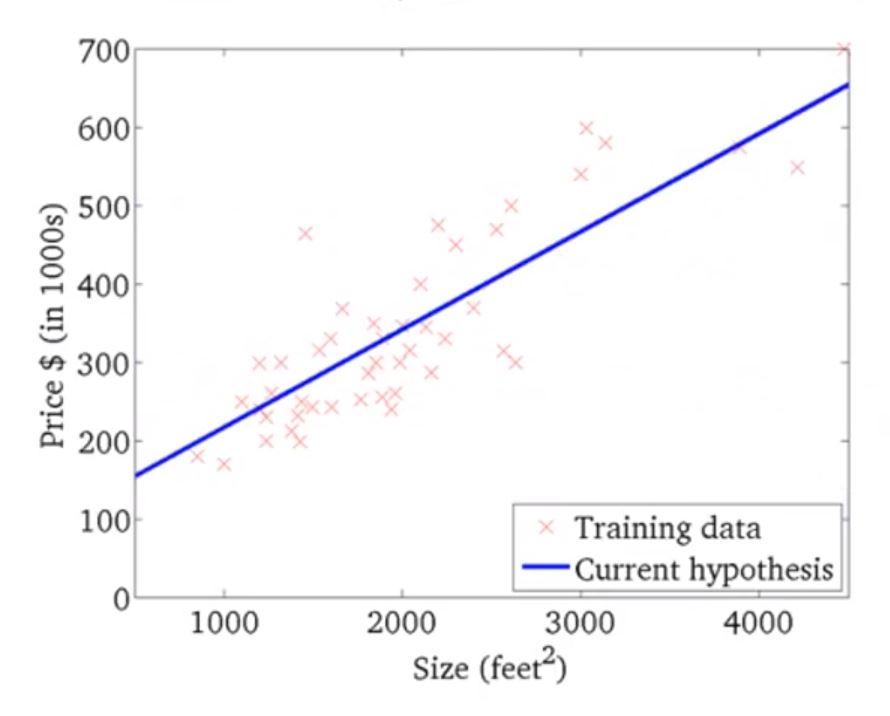
这里的梯度下降又称为批处理梯度下降（"Batch" Gradient Descent）
"Batch": Each step of gradient descent uses all the training examples.
梯度下降的每个步骤都使用所有训练示例。
