数据结构与算法【Java】08---树结构的实际应用
前言
数据 data 结构(structure)是一门 研究组织数据方式的学科,有了编程语言也就有了数据结构.学好数据结构才可以编写出更加漂亮,更加有效率的代码。
- 要学习好数据结构就要多多考虑如何将生活中遇到的问题,用程序去实现解决.
- 程序 = 数据结构 + 算法
- 数据结构是算法的基础, 换言之,想要学好算法,需要把数据结构学到位
我会用数据结构与算法【Java】这一系列的博客记录自己的学习过程,如有遗留和错误欢迎大家提出,我会第一时间改正!!!
注:数据结构与算法【Java】这一系列的博客参考于B站尚硅谷的视频,文章仅用于学习交流,视频原地址为【尚硅谷】数据结构与算法(Java数据结构与算法),大家记得一键三连哦~
上一篇文章数据结构与算法【Java】07---树结构基础部分
1、堆排序
1.1、堆排序简介
1.堆排序是利用堆这种数据结构而设计的一种排序算法,堆排序是一种选择排序,它的最坏,最好,平均时间复杂度均为 O(nlogn),它是不稳定排序。
-
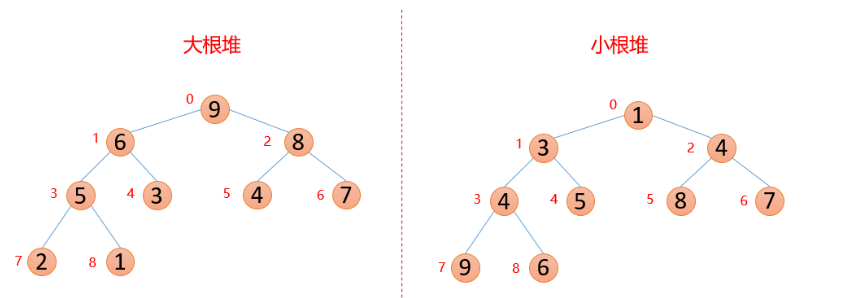
堆是具有以下性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大根堆(或大顶堆), 注意 : 没有
要求结点的左孩子的值和右孩子的值的大小关系。 -
每个结点的值都小于或等于其左右孩子结点的值,称为小根堆(或小顶堆)
-
一般升序采用大根堆,降序采用小根堆

1.2、堆排序过程演示
堆排序的基本思想是:
- 将待排序序列构造成一个大根堆
- 此时,整个序列的最大值就是堆顶的根节点。
- 将其与末尾元素进行交换,此时末尾就为最大值。
- 然后将剩余 n-1 个元素重新构造成一个堆,这样会得到 n 个元素的次小值。如此反复执行,便能得到一个有序
序列了。
步骤图解
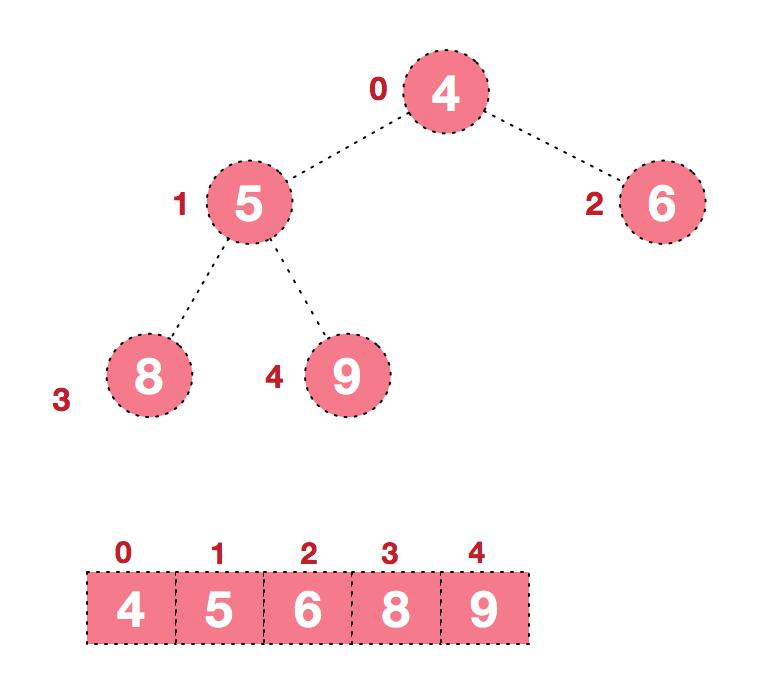
要求:给你一个数组 {4,6,8,5,9} , 要求使用堆排序法,将数组升序排序。
- 步骤一 构造初始堆。将给定无序序列构造成一个大根堆(一般升序采用大根堆,降序采用小根堆)。
- 原始的数组 [4, 6, 8, 5, 9]
-
假设给定无序序列结构如下
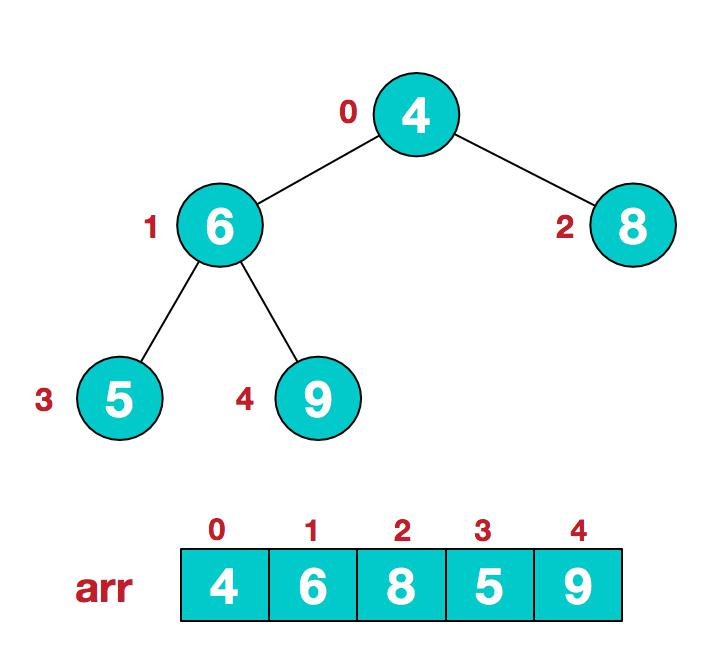
-
此时我们从最后一个非叶子结点开始(叶结点自然不用调整,第一个非叶子结点
arr.length/2-1=5/2-1=1,也就是下面的 6 结点),从左至右,从下至上进行调整。
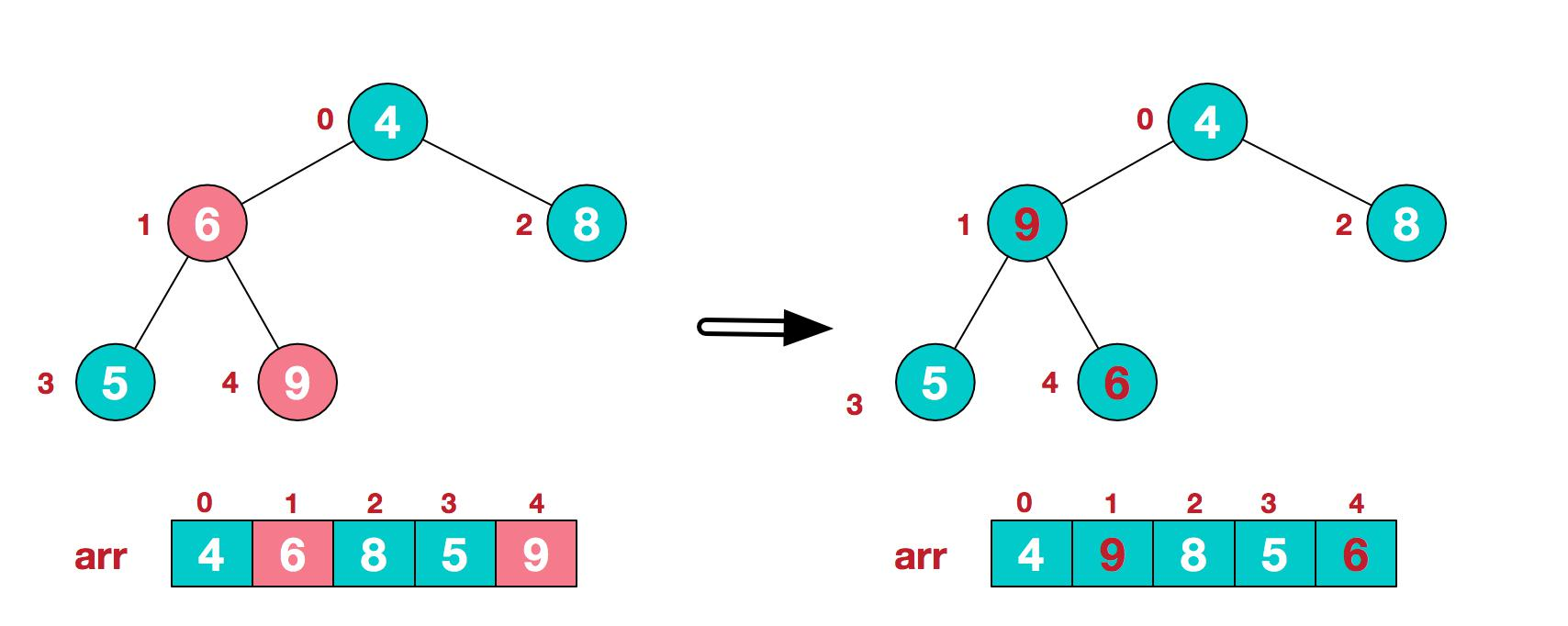
3.找到第二个非叶节点 4,由于[4,9,8]中 9 元素最大,4 和 9 交换。
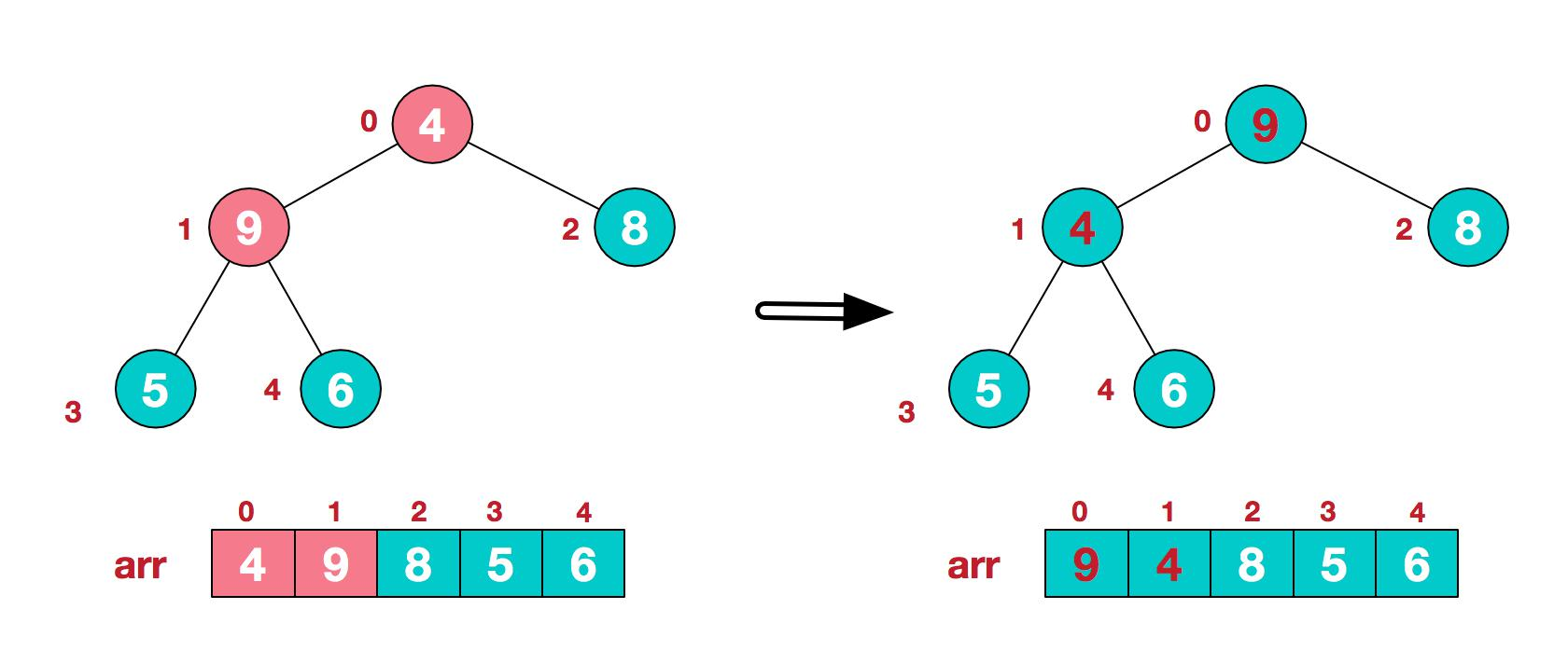
4.这时,交换导致了子根[4,5,6]结构混乱,继续调整,[4,5,6]中 6 最大,交换 4 和 6。
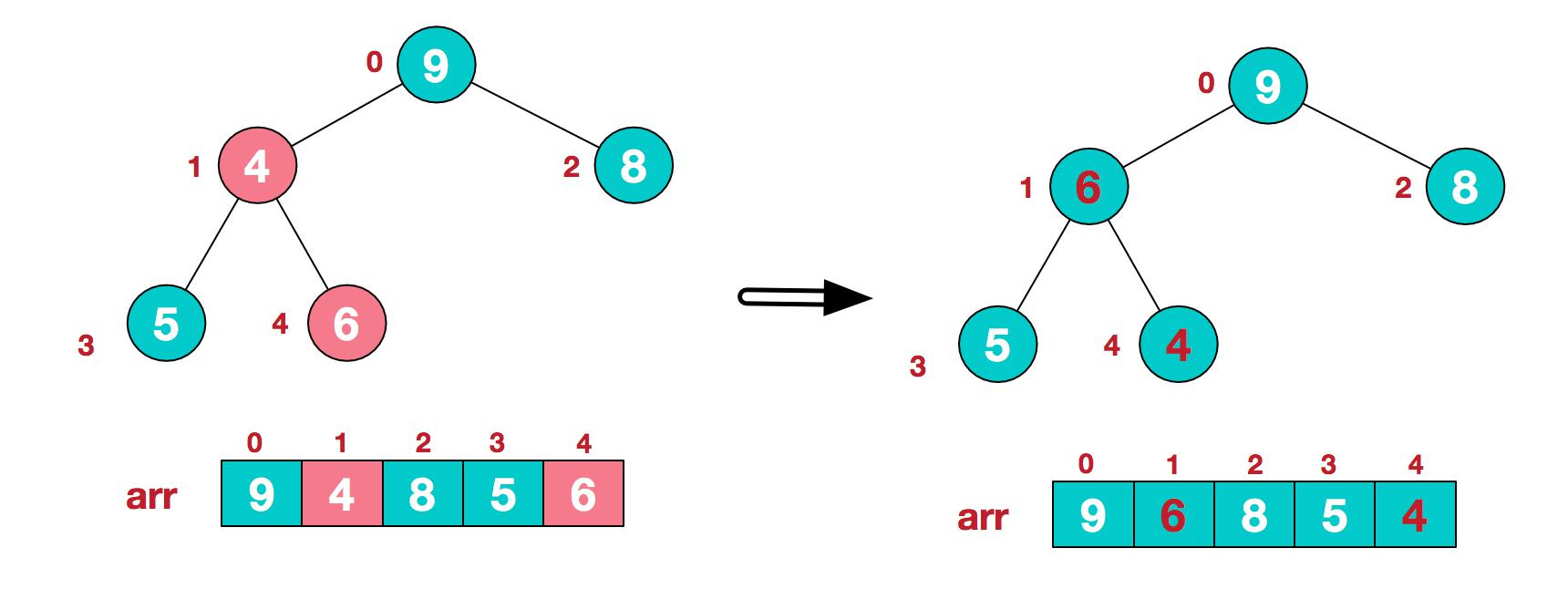
此时,我们就将一个无序序列构造成了一个大顶堆.
- 步骤二 将堆顶元素与末尾元素进行交换,使末尾元素最大。然后继续调整堆,再将堆顶元素与末尾元素交换得到第二大元素。如此反复进行交换、重建、交换
1.将堆顶元素 9 和末尾元素 4 进行交换
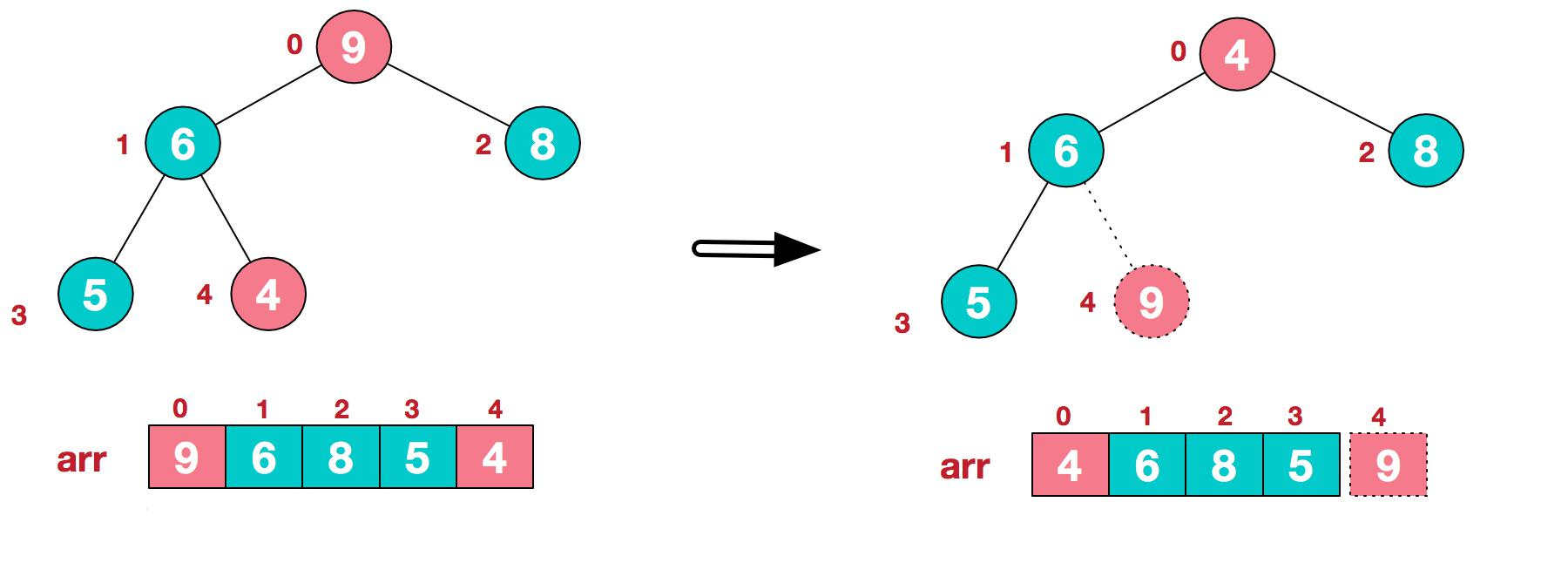
2.重新调整结构,使其继续满足堆定义
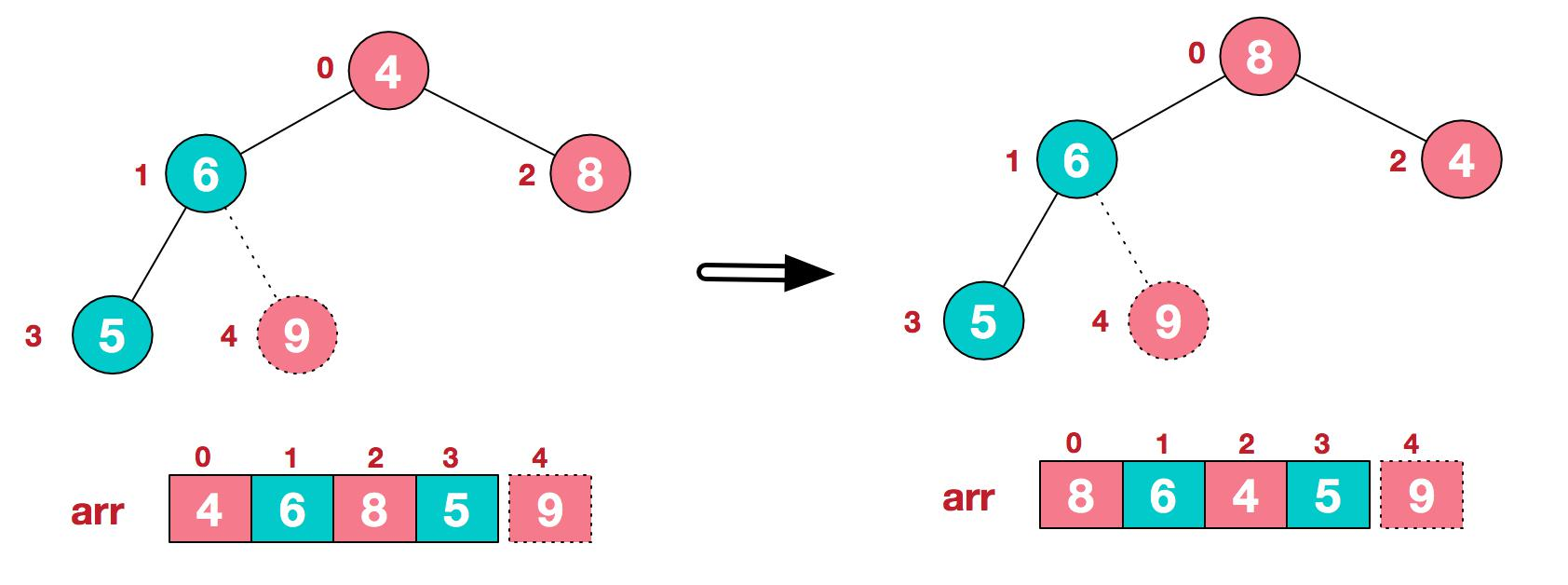
3.再将堆顶元素 8 与末尾元素 5 进行交换,得到第二大元素 8
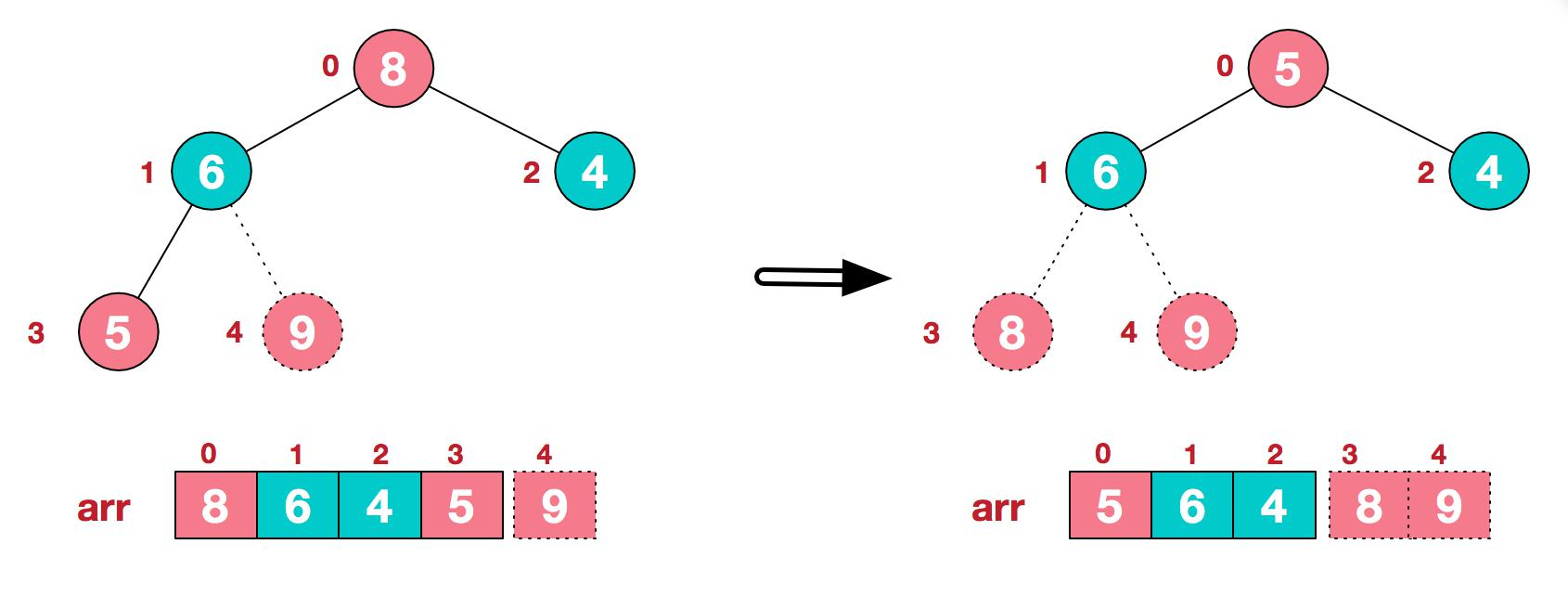
4.后续过程,继续进行调整,交换,如此反复进行,最终使得整个序列有序
再简单总结下堆排序的基本思路:
1).将无序序列构建成一个堆,根据升序降序需求选择大根堆或小根堆;
2).将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端;
3).重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序
动态演示

1.3、堆排序代码实现
堆排序的理解还是比较困难的,尤其是代码实现过程,下面提供两种代码实现,大家可以选择适合自己的实现方法来理解堆排序
代码实现(一)
import java.util.Arrays;
public class HeapSort {
public static void main(String[] args) {
//升序--->大顶堆
long startTime=System.currentTimeMillis();
int arr[] = {5,3,7,1,4,6,2};
heapSort(arr);
long endTime=System.currentTimeMillis();
System.out.println("程序运行时间: "+(endTime-startTime)+"ms");
}
//编写一个堆排序的方法
public static void heapSort(int arr[]) {
int temp = 0;
//完成我们最终代码
//将无序序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆
for(int i = arr.length / 2 -1; i >=0; i--) {
adjustHeap(arr, i, arr.length);
}
/*
* 2).将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端;
3).重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序。
*/
for(int j = arr.length-1;j >0; j--) {
//交换
temp = arr[j];
arr[j] = arr[0];
arr[0] = temp;
adjustHeap(arr, 0, j);
}
System.out.println("数组=" + Arrays.toString(arr));
}
//将一个数组(二叉树), 调整成一个大顶堆
/**
* 功能: 完成 将 以 i 对应的非叶子结点的树调整成大顶堆
* 举例 int arr[] = {4, 6, 8, 5, 9}; => i = 1 => adjustHeap => 得到 {4, 9, 8, 5, 6}
* 如果我们再次调用 adjustHeap 传入的是 i = 0 => 得到 {4, 9, 8, 5, 6} => {9,6,8,5, 4}
* @param arr 待调整的数组
* @param i 表示非叶子结点在数组中索引
* @param length 表示对多少个元素继续调整, length 是在逐渐的减少
*/
public static void adjustHeap(int arr[], int i, int length) {
int temp = arr[i];//先取出当前元素的值,保存在临时变量
//开始调整
//说明
//1. k = i * 2 + 1 k 是 i结点的左子结点
for(int k = i * 2 + 1; k < length; k = k * 2 + 1) {
if(k+1 < length && arr[k] < arr[k+1]) { //说明左子结点的值小于右子结点的值
k++; // k 指向右子结点
}
if(arr[k] > temp) { //如果子结点大于父结点
arr[i] = arr[k]; //把较大的值赋给当前结点
i = k; //!!! i 指向 k,继续循环比较
} else {
break;//!
}
}
//当for 循环结束后,我们已经将以i 为父结点的树的最大值,放在了 最顶(局部)
arr[i] = temp;//将temp值放到调整后的位置
}
}
结果:
代码实现(二)
//交换数组中的元素
public static void swap(int[]num ,int i,int j) {
int temp=num[i];
num[i]=num[j];
num[j]=temp;
}
//将待排序的数组构建成大根堆
public static void buildbigheap(int []num,int end) {
//从最后一个非叶子节点开始构建,依照从下往上,从右往左的顺序
for(int i=end/2;i>=0;i--) {
adjustnode(i, end, num);
}
}
//调整该节点及其以下的所有节点
public static void adjustnode(int i,int end,int []num) {
int left=2*i+1;
int right=2*i+2;
int big=i;
//判断小分支那个是大元素
if(left<end&&num[i]<num[left])
i=left;
if(right<end&&num[i]<num[right])
i=right;
if(i!=big) {
//交换顺序之后需要继续校验
swap(num, i, big);
//重新校验,防止出现交换之后根节点小于孩子节点的情况
adjustnode(i, end, num);
}
}
public static void main(String[] args) {
int []num ={5,3,7,1,4,6,2};
long startTime=System.currentTimeMillis();
//第一次构建大根堆
buildbigheap(num, num.length);
for(int j=num.length-1;j>0;j--) {
System.out.print("第"+(num.length-j)+"次排序前: ");
for(int k=0;k<num.length;k++) {
System.out.print(num[k]+" ");
}
//交换队头已经排序得到的最大元素与队尾元素
swap(num, 0, j);
System.out.print("第"+(num.length-j)+"次排序后: ");
for(int k=0;k<num.length;k++) {
System.out.print(num[k]+" ");
}
System.out.println();
//交换结束之后,大根堆已经被破坏,需要开始重新构建大根堆
buildbigheap(num,j);
}
long endTime=System.currentTimeMillis();
System.out.println("程序运行时间: "+(endTime-startTime)+"ms");
}
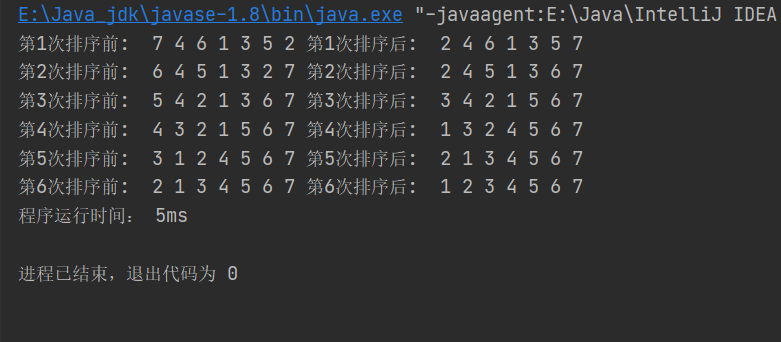
结果:
2、赫夫曼树
2.1、简介
1、给定 n 个权值作为 n 个叶子结点,构造一棵二叉树, 若该树的带权路径长度(wpl) 达到最小,称这样的二叉树为
最优二叉树,也称为哈夫曼树(Huffman Tree), 还有的书翻译为霍夫曼树。
2、赫夫曼树是带权路径长度最短的树,权值较大的结点离根较近
重要概念和举例说明
- 路径和路径长度:在一棵树中,从一个结点往下可以达到的孩子或孙子结点之间的通路,称为路径。通中分支的数目称为路径长度。若规定根结点的层数为 1,则从根结点到第 L 层结点的路径长度为 L-1
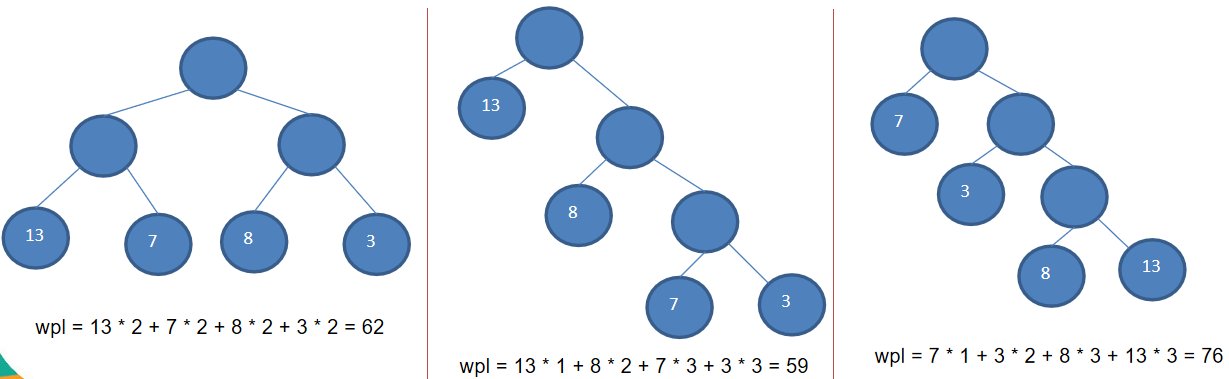
- 结点的权及带权路径长度:若将树中结点赋给一个有着某种含义的数值,则这个数值称为该结点的权。 结
点的带权路径长度为:从根结点到该结点之间的路径长度与该结点的权的乘积 - 树的带权路径长度:树的带权路径长度规定为 所有叶子结点的带权路径长度之和,记为
WPL(weighted path length),权值越大的结点离根结点越近的二叉树才是最优二叉树。 - WPL 最小的就是赫夫曼树
2.2、赫夫曼树创建思路图解
给出一个数列 {13, 7, 8, 3, 29, 6, 1},要求转成一颗赫夫曼树
构成赫夫曼树的步骤:
- 从小到大进行排序, 将每一个数据,每个数据都是一个节点 , 每个节点可以看成是一颗最简单的二叉树
- 取出根节点权值最小的两颗二叉树
- 组成一颗新的二叉树, 该新的二叉树的根节点的权值是前面两颗二叉树根节点权值的和
- 再将这颗新的二叉树,以根节点的权值大小 再次排序, 不断重复 1-2-3-4 的步骤,直到数列中,所有的数
据都被处理,就得到一颗赫夫曼树
图解:
(1)选出最小的两个数组成二叉树
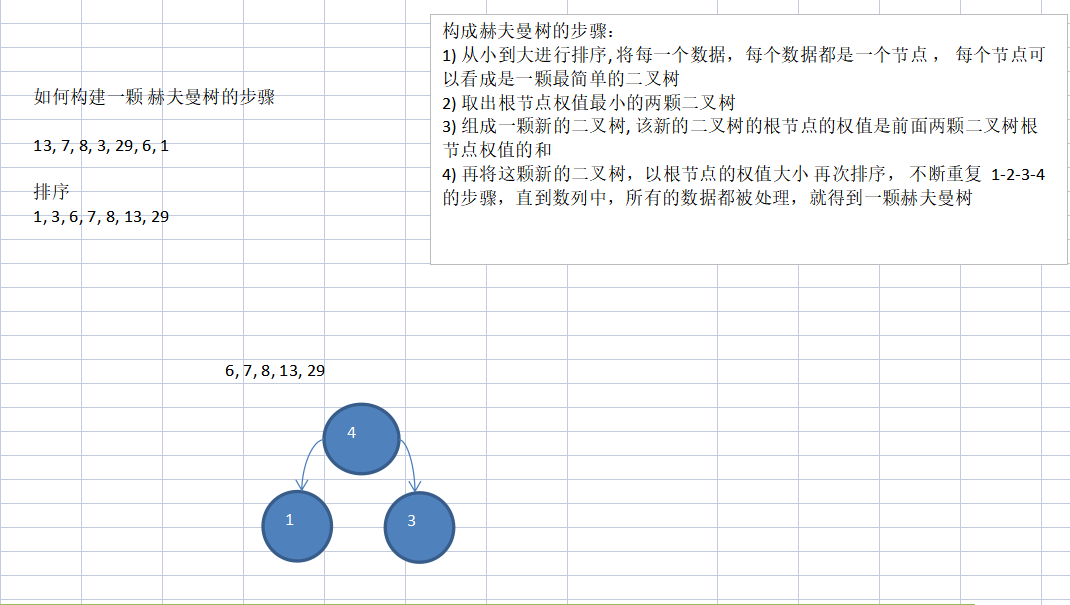
(2)接下来在4,6,7,8...中选择最小的两个4,6(注意这里要加入第一步组成的节点4,大的在右边,小的在左边)
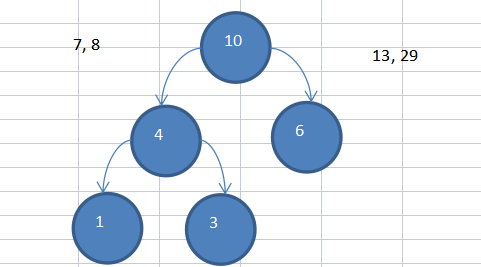
(3)重复上述步骤
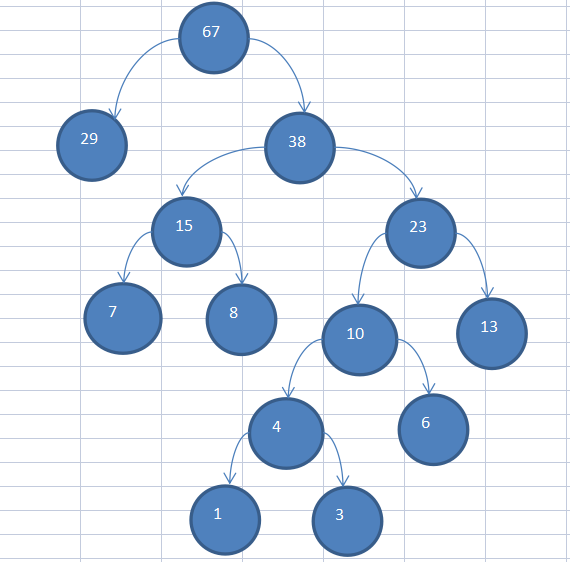
2.3、赫夫曼树代码实现
public class HuffmanTree {
public static void main(String[] args) {
int arr[] = { 13, 7, 8, 3, 29, 6, 1 };
Node root = createHuffmanTree(arr);
preOrder(root); //67,29,38,15,7,8,23,10,4,1,3,6,13
}
//编写一个前序遍历的方法
public static void preOrder(Node root) {
if(root != null) {
root.preOrder();
}else{
System.out.println("是空树,不能遍历~~");
}
}
// 创建赫夫曼树的方法
/**
*
* @param arr 需要创建成哈夫曼树的数组
* @return 创建好后的赫夫曼树的root结点
*/
public static Node createHuffmanTree(int[] arr) {
// 第一步为了操作方便
// 1. 遍历 arr 数组
// 2. 将arr的每个元素构成成一个Node
// 3. 将Node 放入到ArrayList中
List<Node> nodes = new ArrayList<Node>();
for (int value : arr) {
nodes.add(new Node(value));
}
//我们处理的过程是一个循环的过程
while(nodes.size() > 1) {
//排序 从小到大
Collections.sort(nodes);
System.out.println("nodes =" + nodes);
//取出根节点权值最小的两颗二叉树
//(1) 取出权值最小的结点(二叉树)
Node leftNode = nodes.get(0);
//(2) 取出权值第二小的结点(二叉树)
Node rightNode = nodes.get(1);
//(3)构建一颗新的二叉树
Node parent = new Node(leftNode.value + rightNode.value);
parent.left = leftNode;
parent.right = rightNode;
//(4)从ArrayList删除处理过的二叉树
nodes.remove(leftNode);
nodes.remove(rightNode);
//(5)将parent加入到nodes
nodes.add(parent);
}
//返回哈夫曼树的root结点
return nodes.get(0);
}
}
// 创建结点类
// 为了让Node 对象持续排序Collections集合排序
// 让Node 实现Comparable接口
class Node implements Comparable<Node> {
int value; // 结点权值
char c; //字符
Node left; // 指向左子结点
Node right; // 指向右子结点
//写一个前序遍历
public void preOrder() {
System.out.println(this);
if (this.left != null) {
this.left.preOrder();
}
if (this.right != null) {
this.right.preOrder();
}
}
public Node(int value) {
this.value = value;
}
@Override
public String toString() {
return "Node [value=" + value + "]";
}
@Override
public int compareTo(Node o) {
// TODO Auto-generated method stub
// 表示从小到大排序
return this.value - o.value;
}
}
结果:
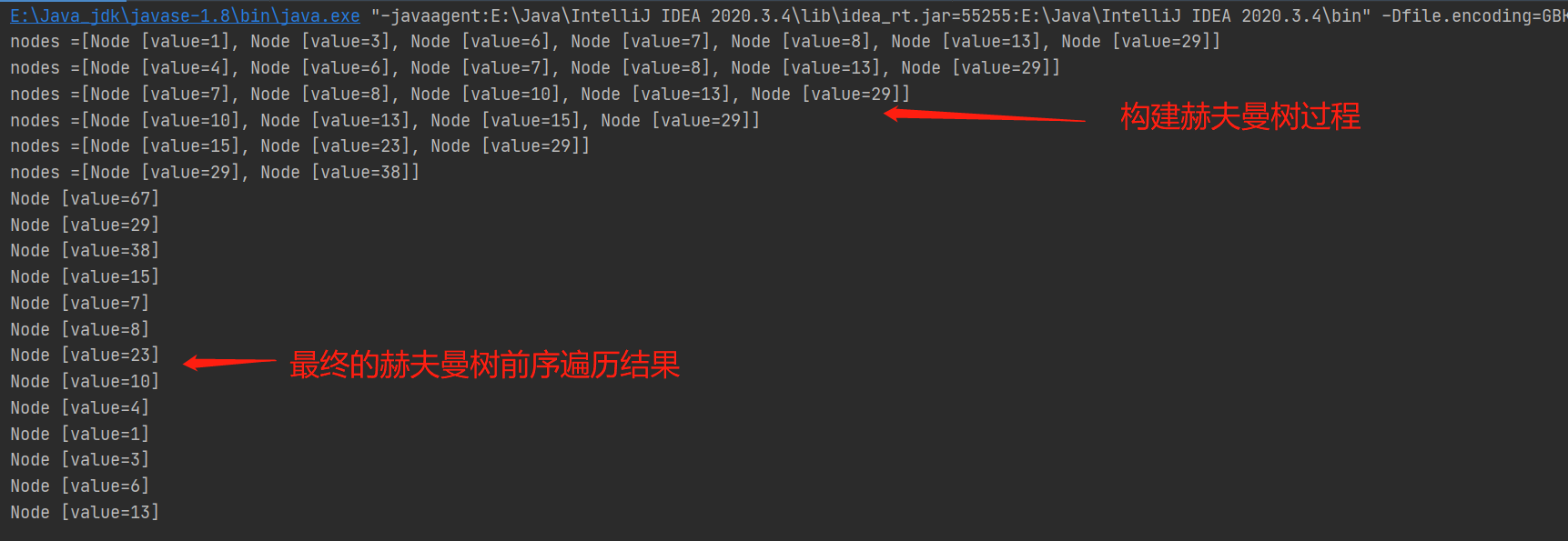
3、赫夫曼编码
3.1、简介
- 赫夫曼编码也翻译为 哈夫曼编码(Huffman Coding),又称霍夫曼编码,是一种编码方式, 属于一种程序算法
- 赫夫曼编码是赫哈夫曼树在电讯通信中的经典的应用之一。
- 赫夫曼编码广泛地用于数据文件压缩。其压缩率通常在 20%~90%之间
- 赫夫曼码是可变字长编码(VLC)的一种。Huffman 于 1952 年提出一种编码方法,称之为最佳编码
3.2、原理剖析
- 通信领域中信息的处理方式 1-定长编码

- 通信领域中信息的处理方式 2-变长编码

- 通信领域中信息的处理方式 3-赫夫曼编码
1、传输的 字符串i like like like java do you like a java
2、d:1 y:1 u:1 j:2 v:2 o:2 l:4 k:4 e:4 i:5 a:5 :9 // 各个字符对应的个数
3、按照上面字符出现的次数构建一颗赫夫曼树, 次数作为权值
构成赫夫曼树的步骤:
- 从小到大进行排序, 将每一个数据,每个数据都是一个节点 , 每个节点可以看成是一颗最简单的二叉树
- 取出根节点权值最小的两颗二叉树
- 组成一颗新的二叉树, 该新的二叉树的根节点的权值是前面两颗二叉树根节点权值的和
- 再将这颗新的二叉树,以根节点的权值大小 再次排序, 不断重复 1-2-3-4 的步骤,直到数列中,所有的数据都被处理,
就得到一颗赫夫曼树
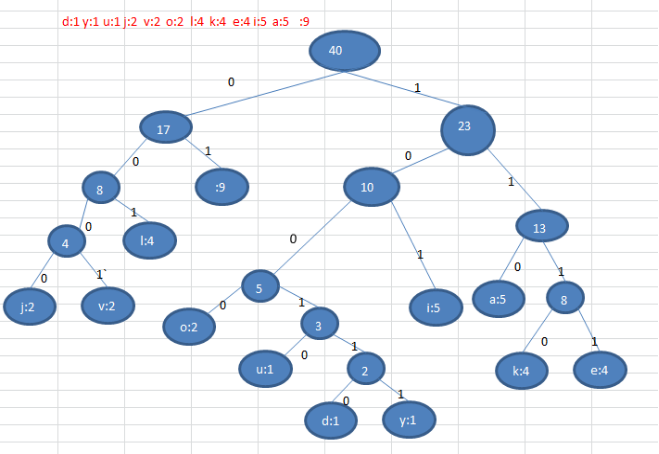
4、根据赫夫曼树,给各个字符,规定编码 (前缀编码), 向左的路径为 0 向右的路径为 1 , 编码如下:
o: 1000
u: 10010
d: 100110
y: 100111
i: 101
a : 110
k: 1110
e: 1111
j: 0000
v: 0001
l: 001
: 01(空格)
5、按照上面的赫夫曼编码,我们的"i like like like java do you like a java" 字符串对应的编码为 (注意这里我们使用的无损压缩)
1010100110111101111010011011110111101001101111011110100001100001110011001111000011001111000100100100110111101111011100100001100001110
通过赫夫曼编码处理 长度为 133,且不会有多义性
6、长度为 : 133
说明:原来长度是359 , 压缩了 (359-133) / 359 = 62.9%
此编码满足前缀编码, 即字符的编码都不能是其他字符编码的前缀。不会造成匹配的多义性
赫夫曼编码是无损处理方案(可以完全恢复)
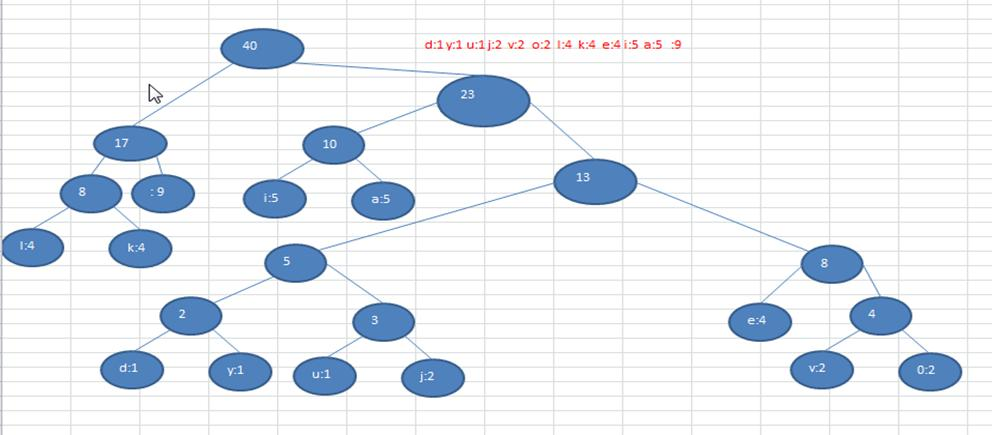
注:这个赫夫曼树根据 排序方法不同,也可能不太一样,这样对应的 赫夫曼编码也不完全一样,但是 wpl 是
一样的,都是最小的, 最后生成的赫夫曼编码的长度是一样,比如: 如果我们让每次生成的新的二叉树总是排在权
值相同的二叉树的最后一个,则生成的二叉树如下图,但是编码长度是不会变的,还是133
3.3、创建赫夫曼树(数据压缩)
将给出的一段文本,比如"i like like like java do you like a java", 根据前面的讲的赫夫曼编码原理,对其进行数
据 压 缩 处 理 , 形 式 如
"1010100110111101111010011011110111101001101111011110100001100001110011001111000011001111000100100100 110111101111011100100001100001110"
功能: 根据赫夫曼编码压缩数据的原理,需要创建 "i like like like java do you like a java" 对应的赫夫曼树
思路:
(1) Node { data (存放数据), weight (权值), left 和 right }
(2) 得到 "i like like like java do you like a java" 对应的 byte[] 数组
(3) 编写一个方法,将准备构建赫夫曼树的Node 节点放到 List , 形式 [Node[date=97 ,weight = 5], Node[]date=32,weight = 9]......], 体现 d:1 y:1 u:1 j:2 v:2 o:2 l:4 k:4 e:4 i:5 a:5 :9
(4) 可以通过List 创建对应的赫夫曼树
代码实现
import java.util.*;
public class HuffmanCode {
public static void main(String[] args) {
String content = "i like like like java do you like a java";
byte[] contentBytes = content.getBytes();
System.out.println(contentBytes.length);//40
List<Node> nodes = getNodes(contentBytes);
System.out.println("nodes="+nodes);
//测试创建的二叉树
System.out.println("创建赫夫曼树:");
Node huffmanTreeRoot = createHuffmanTree(nodes);
System.out.println("前序遍历:");
huffmanTreeRoot.preOrder();
}
//前序遍历的方法
public static void preOrder(Node root){
if (root != null){
root.preOrder();
}else {
System.out.println("赫夫曼树为空");
}
}
/**
*
* @param bytes 接收字节数组
* @return 返回的就是 List 形式 [Node[date=97 ,weight = 5], Node[]date=32,weight = 9]......],
*/
private static List<Node> getNodes(byte[] bytes){
//1.创建一个ArrayList
ArrayList<Node> nodes = new ArrayList<>();
//遍历bytes,存储每一个byte出现的次数=》map[key,value]
HashMap<Byte,Integer> counts = new HashMap<>();
for (byte b: bytes) {
Integer count = counts.get(b);
if (count == null){//Map还没有这个数据
counts.put(b,1);
}else {
counts.put(b,count+1);
}
}
//把每个键值对转成一个Node对象,并加入到nodes集合
//遍历map
for (Map.Entry<Byte,Integer> entry : counts.entrySet()){
nodes.add(new Node(entry.getKey(), entry.getValue()));
}
return nodes;
}
//通过list创建应的赫夫曼树
private static Node createHuffmanTree(List<Node> nodes){
while (nodes.size() > 1){
//排序,从小到大
Collections.sort(nodes);
//取出第一棵最小的二叉树左节点
Node leftNode = nodes.get(0);
//取出第二棵最小的二叉树右节点
Node rightNode = nodes.get(1);
//创建一棵新的二叉树,它的根节点没有data,只有权值
Node parent = new Node(null, leftNode.weight+ rightNode.weight);
parent.left = leftNode;
parent.right = rightNode;
//将已经处理的两棵二叉树从nodes删除
nodes.remove(leftNode);
nodes.remove(rightNode);
//将新的二叉树加入到nodes
nodes.add(parent);
}
//nodes 最后的节点就是赫夫曼树的根节点
return nodes.get(0);
}
}
//创建Node,带数据和权值
class Node implements Comparable<Node>{
Byte data;//存放数据本身 a===>97 ascii码
int weight;//权值,表示字符出现的次数
Node left;
Node right;
public Node(Byte data, int weight) {
this.data = data;
this.weight = weight;
}
@Override
public int compareTo(Node o) {
//从小到大排序
return this.weight-o.weight;
}
public String toString() {
return "Node [data = " + data + " weight=" + weight + "]";
}
//前序遍历
public void preOrder() {
System.out.println(this);
if(this.left != null) {
this.left.preOrder();
}
if(this.right != null) {
this.right.preOrder();
}
}
}
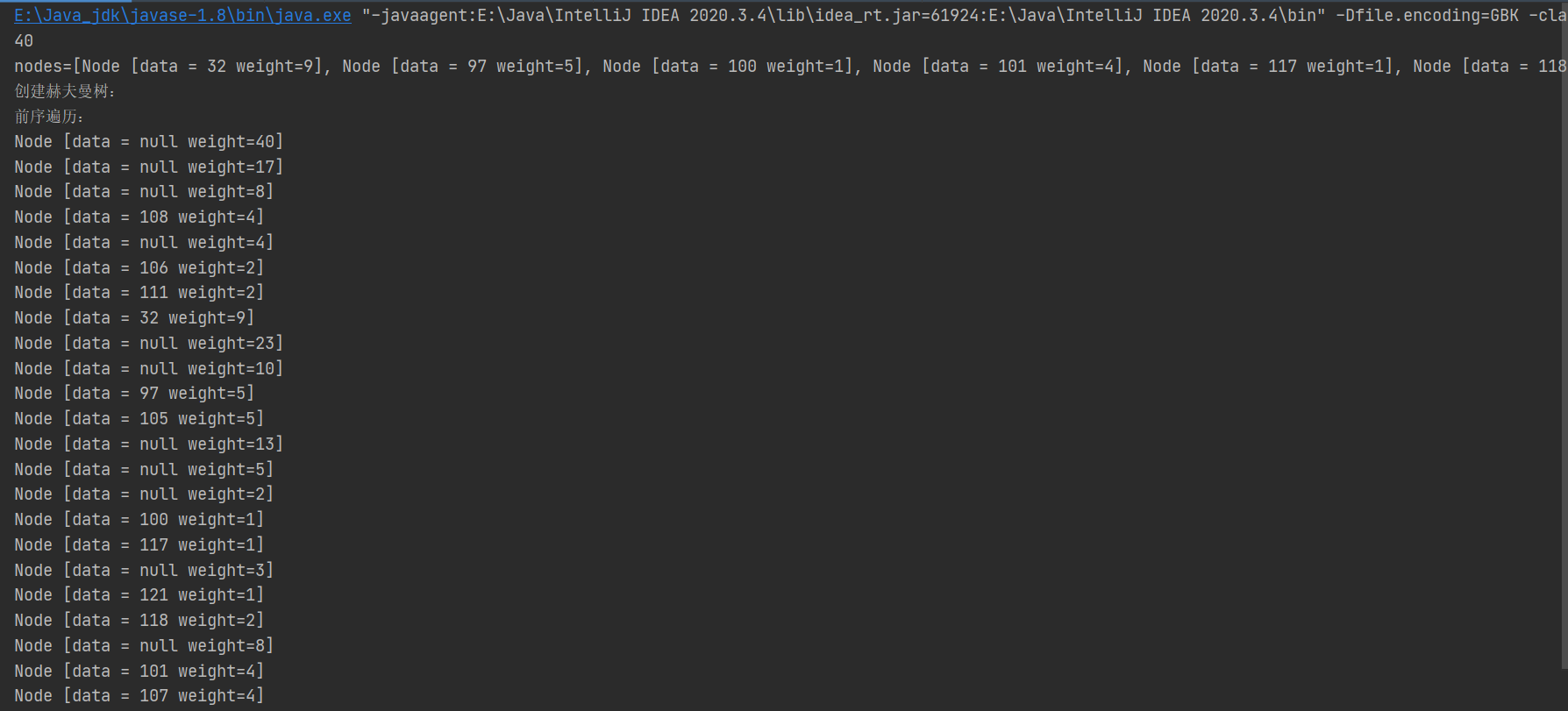
结果:(创建出赫夫曼树前序遍历)
3.4、生成赫夫曼编码和赫夫曼编码后的数据(数据压缩)
我们已经生成了 赫夫曼树, 下面我们继续完成任务
- 生成赫夫曼树对应的赫夫曼编码 , 如下表:
=01 a=100 d=11000 u=11001 e=1110 v=11011 i=101 y=11010 j=0010 k=1111 l=000 o=0011 - 使用赫夫曼编码来生成赫夫曼编码数据 ,即按照上面的赫夫曼编码,将"i like like like java do you like a java"
字符串生成对应的编码数据, 形式如下.
10101000101111111100100010111111110010001011111111001001010011011100011100000110111010001111001010 00101111111100110001001010011011100
1、生成赫夫曼树对应的赫夫曼编码
代码实现
//测试是否生成了对应的赫夫曼编码
Map<Byte, String> huffmanCodes = getCodes(huffmanTreeRoot);
System.out.println("生成的对应的赫夫曼编码="+ HuffmanCode.huffmanCodes);
//...
//生成赫夫曼树对应的赫夫曼编码
//思路:
//1. 将赫夫曼编码表存放在 Map<Byte,String> 形式
// 生成的赫夫曼编码表{32(空格)=01, 97(a)=100, 100(...)=11000, 117=11001, 101=1110, 118=11011, 105=101, 121=11010, 106=0010, 107=1111, 108=000, 111=0011}
static Map<Byte, String> huffmanCodes = new HashMap<Byte,String>();
//2. 在生成赫夫曼编码表示,需要去拼接路径, 定义一个StringBuilder 存储某个叶子结点的路径
static StringBuilder stringBuilder = new StringBuilder();
//为了调用方便,我们重载 getCodes
private static Map<Byte, String> getCodes(Node root) {
if(root == null) {
return null;
}
//处理root的左子树
getCodes(root.left, "0", stringBuilder);
//处理root的右子树
getCodes(root.right, "1", stringBuilder);
return huffmanCodes;
}
/**
* 功能:将传入的node结点的所有叶子结点的赫夫曼编码得到,并放入到huffmanCodes集合
* @param node 传入结点
* @param code 路径: 左子结点是 0, 右子结点 1
* @param stringBuilder 用于拼接路径
*/
private static void getCodes(Node node,String code,StringBuilder stringBuilder){
StringBuilder stringBuilder2 = new StringBuilder(stringBuilder);
//将code加入到 stringBuilder2 (拼接路径)
stringBuilder2.append(code);
if (node != null){//如果node等于空,不处理
//判断当前node是叶子节点还是非叶子结点
if (node.data == null){//非叶子节点
//递归处理
//向左递归
getCodes(node.left, "0", stringBuilder2);
//向右递归
getCodes(node.right, "1", stringBuilder2);
}else {//进入到这里说明是叶子节点,找到了最后
huffmanCodes.put(node.data,stringBuilder2.toString());
}
}
}
结果:

2、使用赫夫曼编码来生成赫夫曼编码数据
代码实现
//测试返回byte数组
byte[] huffmanCodeBytes = zip(contentBytes, huffmanCodes);
System.out.println("huffmanCodeBytes="+Arrays.toString(huffmanCodeBytes));//17
//...
//编写一个方法,将字符串对应的byte[] 数组,通过生成的赫夫曼编码表,返回一个赫夫曼编码 压缩后的byte[]
/**
*
* @param bytes 这是原始的字符串对应的 byte[]
* @param huffmanCodes 生成的赫夫曼编码map
* @return 返回赫夫曼编码处理后的 byte[]
* 举例: String content = "i like like like java do you like a java"; =》 byte[] contentBytes = content.getBytes();
* 返回的是 字符串 "1010100010111111110010001011111111001000101111111100100101001101110001110000011011101000111100101000101111111100110001001010011011100"
* => 对应的 byte[] huffmanCodeBytes ,即 8位对应一个 byte,放入到 huffmanCodeBytes
* huffmanCodeBytes[0] = 10101000(补码) => byte [推导 10101000=> 10101000 - 1 => 10100111(反码)=> 11011000(原码)= -88 ]
* huffmanCodeBytes[1] = -88
*/
private static byte[] zip(byte[] bytes, Map<Byte, String> huffmanCodes) {
//1.利用 huffmanCodes 将 bytes 转成 赫夫曼编码对应的字符串
StringBuilder stringBuilder = new StringBuilder();
//遍历bytes 数组
for(byte b: bytes) {
stringBuilder.append(huffmanCodes.get(b));
}
//System.out.println("测试 stringBuilder~~~=" + stringBuilder.toString());
//将 "1010100010111111110..." 转成 byte[]
//统计返回 byte[] huffmanCodeBytes 长度
//一句话 int len = (stringBuilder.length() + 7) / 8;
int len;
if(stringBuilder.length() % 8 == 0) {
len = stringBuilder.length() / 8;
} else {
len = stringBuilder.length() / 8 + 1;
}
//创建 存储压缩后的 byte数组
byte[] huffmanCodeBytes = new byte[len];
int index = 0;//记录是第几个byte
for (int i = 0; i < stringBuilder.length(); i += 8) { //因为是每8位对应一个byte,所以步长 +8
String strByte;
if(i+8 > stringBuilder.length()) {//不够8位
strByte = stringBuilder.substring(i);
}else{
strByte = stringBuilder.substring(i, i + 8);
}
//将strByte 转成一个byte,放入到 huffmanCodeBytes
huffmanCodeBytes[index] = (byte)Integer.parseInt(strByte, 2);
index++;
}
return huffmanCodeBytes;
}
3.5、数据压缩小结
将3.3与3.4中编写的所有方法封装成一个方法
//使用一个方法,将前面的方法封装起来,便于我们的调用
/**
* @param bytes 原始的字符串对应的字节数组
* @return 是经过 赫夫曼编码处理后的字节数组(压缩后的数组)
*/
private static byte[] huffmanZip(byte[] bytes){
List<Node> nodes = getNodes(bytes);
//根据nodes创建的赫夫曼树
Node huffmanTreeRoot = createHuffmanTree(nodes);
//生成对应的赫夫曼编码(根据赫夫曼树)
Map<Byte, String> huffmanCodes = getCodes(huffmanTreeRoot);
//根据生成的赫夫曼编码来对原始的字节数组进行压缩
byte[] huffmanCodeBytes = zip(bytes, huffmanCodes);
return huffmanCodeBytes;
}
数据压缩的所有代码
import java.util.*;
public class HuffmanCode {
public static void main(String[] args) {
String content = "i like like like java do you like a java";
byte[] contentBytes = content.getBytes();
System.out.println("原始的content字符串长度为:"+contentBytes.length);//40
byte[] huffmanCodesBytes = huffmanZip(contentBytes);
System.out.println("对content字符串压缩后的结果是:"+Arrays.toString(huffmanCodesBytes));
System.out.println("长度为:"+huffmanCodesBytes.length);//17
}
//使用一个方法,将前面的方法封装起来,便于我们的调用
/**
* @param bytes 原始的字符串对应的字节数组
* @return 是经过 赫夫曼编码处理后的字节数组(压缩后的数组)
*/
private static byte[] huffmanZip(byte[] bytes){
List<Node> nodes = getNodes(bytes);
//根据nodes创建的赫夫曼树
Node huffmanTreeRoot = createHuffmanTree(nodes);
//生成对应的赫夫曼编码(根据赫夫曼树)
Map<Byte, String> huffmanCodes = getCodes(huffmanTreeRoot);
//根据生成的赫夫曼编码来对原始的字节数组进行压缩
byte[] huffmanCodeBytes = zip(bytes, huffmanCodes);
return huffmanCodeBytes;
}
//编写一个方法,将字符串对应的byte[] 数组,通过生成的赫夫曼编码表,返回一个赫夫曼编码 压缩后的byte[]
/**
*
* @param bytes 这是原始的字符串对应的 byte[]
* @param huffmanCodes 生成的赫夫曼编码map
* @return 返回赫夫曼编码处理后的 byte[]
* 举例: String content = "i like like like java do you like a java"; =》 byte[] contentBytes = content.getBytes();
* 返回的是 字符串 "1010100010111111110010001011111111001000101111111100100101001101110001110000011011101000111100101000101111111100110001001010011011100"
* => 对应的 byte[] huffmanCodeBytes ,即 8位对应一个 byte,放入到 huffmanCodeBytes
* huffmanCodeBytes[0] = 10101000(补码) => byte [推导 10101000=> 10101000 - 1 => 10100111(反码)=> 11011000(原码)= -88 ]
* huffmanCodeBytes[1] = -88
*/
private static byte[] zip(byte[] bytes, Map<Byte, String> huffmanCodes) {
//1.利用 huffmanCodes 将 bytes 转成 赫夫曼编码对应的字符串
StringBuilder stringBuilder = new StringBuilder();
//遍历bytes 数组
for(byte b: bytes) {
stringBuilder.append(huffmanCodes.get(b));
}
//System.out.println("测试 stringBuilder~~~=" + stringBuilder.toString());
//将 "1010100010111111110..." 转成 byte[]
//统计返回 byte[] huffmanCodeBytes 长度
//一句话 int len = (stringBuilder.length() + 7) / 8;
int len;
if(stringBuilder.length() % 8 == 0) {
len = stringBuilder.length() / 8;
} else {
len = stringBuilder.length() / 8 + 1;
}
//创建 存储压缩后的 byte数组
byte[] huffmanCodeBytes = new byte[len];
int index = 0;//记录是第几个byte
for (int i = 0; i < stringBuilder.length(); i += 8) { //因为是每8位对应一个byte,所以步长 +8
String strByte;
if(i+8 > stringBuilder.length()) {//不够8位
strByte = stringBuilder.substring(i);
}else{
strByte = stringBuilder.substring(i, i + 8);
}
//将strByte 转成一个byte,放入到 huffmanCodeBytes
huffmanCodeBytes[index] = (byte)Integer.parseInt(strByte, 2);
index++;
}
return huffmanCodeBytes;
}
//生成赫夫曼树对应的赫夫曼编码
//思路:
//1. 将赫夫曼编码表存放在 Map<Byte,String> 形式
// 生成的赫夫曼编码表{32(空格)=01, 97(a)=100, 100(...)=11000, 117=11001, 101=1110, 118=11011, 105=101, 121=11010, 106=0010, 107=1111, 108=000, 111=0011}
static Map<Byte, String> huffmanCodes = new HashMap<Byte,String>();
//2. 在生成赫夫曼编码表示,需要去拼接路径, 定义一个StringBuilder 存储某个叶子结点的路径
static StringBuilder stringBuilder = new StringBuilder();
//为了调用方便,我们重载 getCodes
private static Map<Byte, String> getCodes(Node root) {
if(root == null) {
return null;
}
//处理root的左子树
getCodes(root.left, "0", stringBuilder);
//处理root的右子树
getCodes(root.right, "1", stringBuilder);
return huffmanCodes;
}
/**
* 功能:将传入的node结点的所有叶子结点的赫夫曼编码得到,并放入到huffmanCodes集合
* @param node 传入结点
* @param code 路径: 左子结点是 0, 右子结点 1
* @param stringBuilder 用于拼接路径
*/
private static void getCodes(Node node,String code,StringBuilder stringBuilder){
StringBuilder stringBuilder2 = new StringBuilder(stringBuilder);
//将code加入到 stringBuilder2 (拼接路径)
stringBuilder2.append(code);
if (node != null){//如果node等于空,不处理
//判断当前node是叶子节点还是非叶子结点
if (node.data == null){//非叶子节点
//递归处理
//向左递归
getCodes(node.left, "0", stringBuilder2);
//向右递归
getCodes(node.right, "1", stringBuilder2);
}else {//进入到这里说明是叶子节点,找到了最后
huffmanCodes.put(node.data,stringBuilder2.toString());
}
}
}
//前序遍历的方法
public static void preOrder(Node root){
if (root != null){
root.preOrder();
}else {
System.out.println("赫夫曼树为空");
}
}
/**
*
* @param bytes 接收字节数组
* @return 返回的就是 List 形式 [Node[date=97 ,weight = 5], Node[]date=32,weight = 9]......],
*/
private static List<Node> getNodes(byte[] bytes){
//1.创建一个ArrayList
ArrayList<Node> nodes = new ArrayList<>();
//遍历bytes,存储每一个byte出现的次数=》map[key,value]
HashMap<Byte,Integer> counts = new HashMap<>();
for (byte b: bytes) {
Integer count = counts.get(b);
if (count == null){//Map还没有这个数据
counts.put(b,1);
}else {
counts.put(b,count+1);
}
}
//把每个键值对转成一个Node对象,并加入到nodes集合
//遍历map
for (Map.Entry<Byte,Integer> entry : counts.entrySet()){
nodes.add(new Node(entry.getKey(), entry.getValue()));
}
return nodes;
}
//通过list创建应的赫夫曼树
private static Node createHuffmanTree(List<Node> nodes){
while (nodes.size() > 1){
//排序,从小到大
Collections.sort(nodes);
//取出第一棵最小的二叉树左节点
Node leftNode = nodes.get(0);
//取出第二棵最小的二叉树右节点
Node rightNode = nodes.get(1);
//创建一棵新的二叉树,它的根节点没有data,只有权值
Node parent = new Node(null, leftNode.weight+ rightNode.weight);
parent.left = leftNode;
parent.right = rightNode;
//将已经处理的两棵二叉树从nodes删除
nodes.remove(leftNode);
nodes.remove(rightNode);
//将新的二叉树加入到nodes
nodes.add(parent);
}
//nodes 最后的节点就是赫夫曼树的根节点
return nodes.get(0);
}
}
//创建Node,带数据和权值
class Node implements Comparable<Node>{
Byte data;//存放数据本身 a===>97 ascii码
int weight;//权值,表示字符出现的次数
Node left;
Node right;
public Node(Byte data, int weight) {
this.data = data;
this.weight = weight;
}
@Override
public int compareTo(Node o) {
//从小到大排序
return this.weight-o.weight;
}
public String toString() {
return "Node [data = " + data + " weight=" + weight + "]";
}
//前序遍历
public void preOrder() {
System.out.println(this);
if(this.left != null) {
this.left.preOrder();
}
if(this.right != null) {
this.right.preOrder();
}
}
}
数据压缩的结果:

压缩率:(40-17)/40=57.5%
3.6、使用赫夫曼编码解码(数据解压)
使用赫夫曼编码来解码数据,具体要求是
- 前面我们得到了赫夫曼编码和对应的编码
byte[] , 即:[-88, -65, -56, -65, -56, -65, -55, 77, -57, 6, -24, -14, -117, -4, -60, -90, 28] - 现在要求使用赫夫曼编码, 进行解码,又
重新得到原来的字符串"i like like like java do you like a java"
在数据解压的过程中我们需要两个方法,一个是将压缩后的结果转为二进制的字符串,一个是对压缩数据进行解码
/**
* 将一个byte 转成一个二进制的字符串, 这里需要利用二进制的原码,反码,补码
* @param b 传入的 byte
* @param flag 标志是否需要补高位如果是true ,表示需要补高位,如果是false表示不补, 如果是最后一个字节,无需补高位
* @return 是该b 对应的二进制的字符串,(注意是按补码返回)
*/
private static String byteToBitString(boolean flag, byte b) {
//使用变量保存 b
int temp = b; //将 b 转成 int
//如果是正数我们还存在补高位
if(flag) {
temp |= 256; //按位与 256 1 0000 0000 | 0000 0001 => 1 0000 0001
}
String str = Integer.toBinaryString(temp); //返回的是temp对应的二进制的补码
if(flag) {
return str.substring(str.length() - 8);
} else {
return str;
}
}
//编写一个方法,完成对压缩数据的解码
/**
*
* @param huffmanCodes 赫夫曼编码表 map(key = value)
* @param huffmanBytes 赫夫曼编码得到的字节数组
* @return 就是原来的字符串对应的数组
*/
private static byte[] decode(Map<Byte,String> huffmanCodes, byte[] huffmanBytes) {
//1. 先得到 huffmanBytes 对应的 二进制的字符串 , 形式 1010100010111...
StringBuilder stringBuilder = new StringBuilder();
//将byte数组转成二进制的字符串
for(int i = 0; i < huffmanBytes.length; i++) {
byte b = huffmanBytes[i];
//判断是不是最后一个字节
boolean flag = (i == huffmanBytes.length - 1);
stringBuilder.append(byteToBitString(!flag, b));
}
//把字符串按照指定的赫夫曼编码进行解码
//把赫夫曼编码表进行调换,因为反向查询 a->100 100->a
Map<String, Byte> map = new HashMap<String,Byte>();
for(Map.Entry<Byte, String> entry: huffmanCodes.entrySet()) {
map.put(entry.getValue(), entry.getKey());
//key = value 变成 value = key
}
//创建要给集合,存放byte
List<Byte> list = new ArrayList<>();
//i 可以理解成就是索引,扫描 stringBuilder
for(int i = 0; i < stringBuilder.length(); ) {
int count = 1; // 小的计数器
boolean flag = true;
Byte b = null;
while(flag) {
//1010100010111...
//递增的取出 key 1 (1,10,101...匹配)
String key = stringBuilder.substring(i, i+count);//i 不动,让count移动,指定匹配到一个字符
b = map.get(key);
if(b == null) {//说明没有匹配到
count++;
}else {
//匹配到
flag = false;
}
}
list.add(b);
i += count;//i 直接移动到 count
}
//当for循环结束后,我们list中就存放了所有的字符 "i like like like java do you like a java"
//把list 中的数据放入到byte[] 并返回
byte b[] = new byte[list.size()];
for(int i = 0;i < b.length; i++) {
b[i] = list.get(i);
}
return b;
}
测试
//解压
byte[] sourceBytes = decode(huffmanCodes, huffmanCodesBytes);
System.out.println("(解压后)原来的字符串="+new String(sourceBytes));

3.6、文件压缩
我们学习了通过赫夫曼编码对一个字符串进行编码和解码, 下面我们来完成对文件的压缩和解压, 具体要求:
给你一个图片文件,要求对其进行无损压缩, 看看压缩效果如何
思路:读取文件-> 得到赫夫曼编码表 -> 完成压缩
首先我们创建一个图片文件

压缩代码
//编写方法,将一个文件进行压缩
/**
*
* @param srcFile 你传入的希望压缩的文件的全路径
* @param dstFile 我们压缩后将压缩文件放到哪个目录
*/
public static void zipFile(String srcFile, String dstFile) {
//创建输出流
OutputStream os = null;
ObjectOutputStream oos = null;
//创建文件的输入流
FileInputStream is = null;
try {
//创建文件的输入流
is = new FileInputStream(srcFile);
//创建一个和源文件大小一样的byte[]
byte[] b = new byte[is.available()];
//读取文件
is.read(b);
//直接对源文件压缩
byte[] huffmanBytes = huffmanZip(b);
//创建文件的输出流, 存放压缩文件
os = new FileOutputStream(dstFile);
//创建一个和文件输出流关联的ObjectOutputStream
oos = new ObjectOutputStream(os);
//把 赫夫曼编码后的字节数组写入压缩文件
oos.writeObject(huffmanBytes);
//这里我们以对象流的方式写入 赫夫曼编码,是为了以后我们恢复源文件时使用
//注意一定要把赫夫曼编码 写入压缩文件
oos.writeObject(huffmanCodes);
}catch (Exception e) {
System.out.println(e.getMessage());
}finally {
try {
is.close();
oos.close();
os.close();
}catch (Exception e) {
System.out.println(e.getMessage());
}
}
}
测试代码
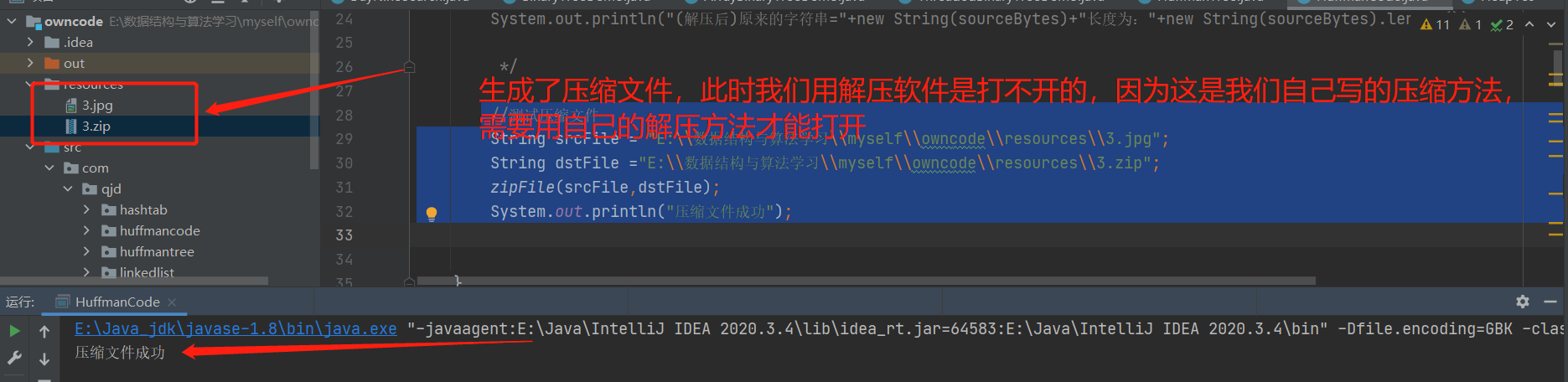
//测试压缩文件
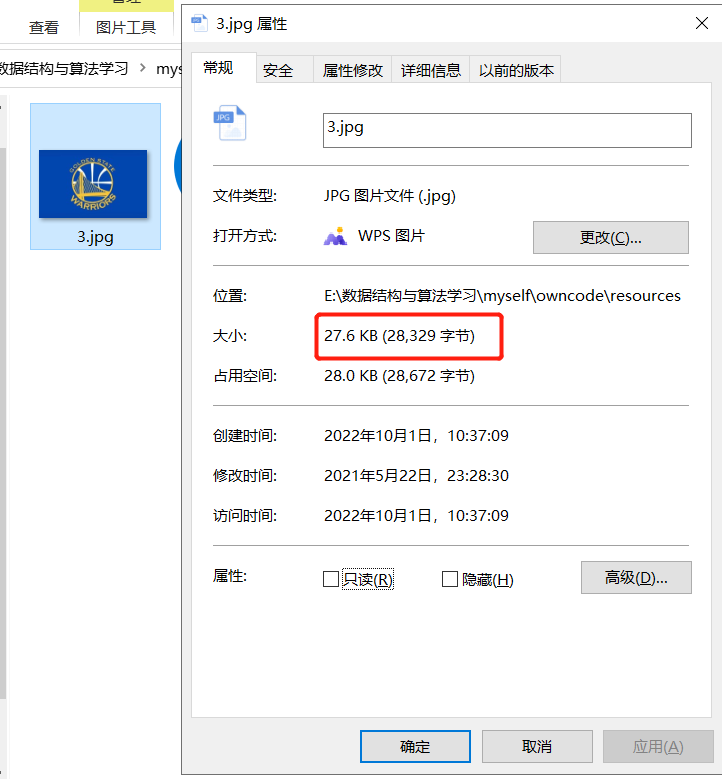
String srcFile = "E:\\数据结构与算法学习\\myself\\owncode\\resources\\3.jpg";
String dstFile ="E:\\数据结构与算法学习\\myself\\owncode\\resources\\3.zip";
zipFile(srcFile,dstFile);
System.out.println("压缩文件成功");
结果
3.7、文件解压
具体要求:将前面压缩的文件,重新恢复成原来的文件。
思路:读取压缩文件(数据和赫夫曼编码表)-> 完成解压(文件恢复)
文件解压代码
//编写一个方法,完成对压缩文件的解压
/**
*
* @param zipFile 准备解压的文件
* @param dstFile 将文件解压到哪个路径
*/
public static void unZipFile(String zipFile, String dstFile) {
//定义文件输入流
InputStream is = null;
//定义一个对象输入流
ObjectInputStream ois = null;
//定义文件的输出流
OutputStream os = null;
try {
//创建文件输入流
is = new FileInputStream(zipFile);
//创建一个和 is关联的对象输入流
ois = new ObjectInputStream(is);
//读取byte数组 huffmanBytes
byte[] huffmanBytes = (byte[])ois.readObject();
//读取赫夫曼编码表
Map<Byte,String> huffmanCodes = (Map<Byte,String>)ois.readObject();
//解码
byte[] bytes = decode(huffmanCodes, huffmanBytes);
//将bytes 数组写入到目标文件
os = new FileOutputStream(dstFile);
//写数据到 dstFile 文件
os.write(bytes);
} catch (Exception e) {
System.out.println(e.getMessage());
} finally {
try {
os.close();
ois.close();
is.close();
} catch (Exception e2) {
System.out.println(e2.getMessage());
}
}
}
测试代码
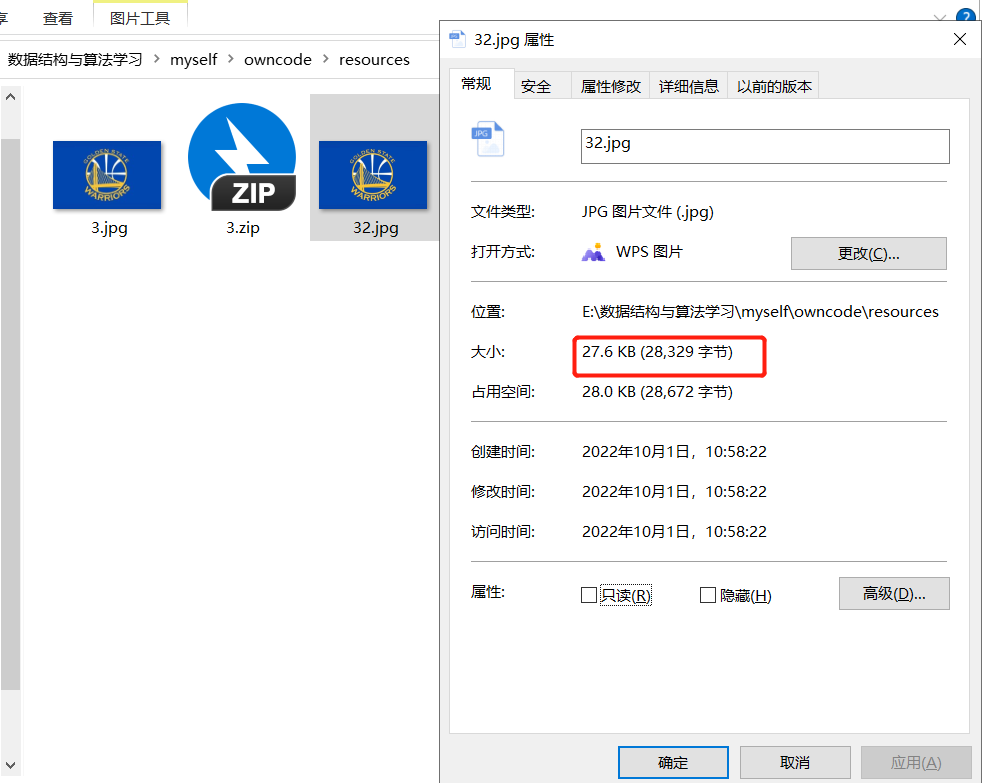
//测试解压文件
String zipFile = "E:\\数据结构与算法学习\\myself\\owncode\\resources\\3.zip";
String dstFile = "E:\\数据结构与算法学习\\myself\\owncode\\resources\\32.jpg";
unZipFile(zipFile,dstFile);
System.out.println("解压成功");
结果
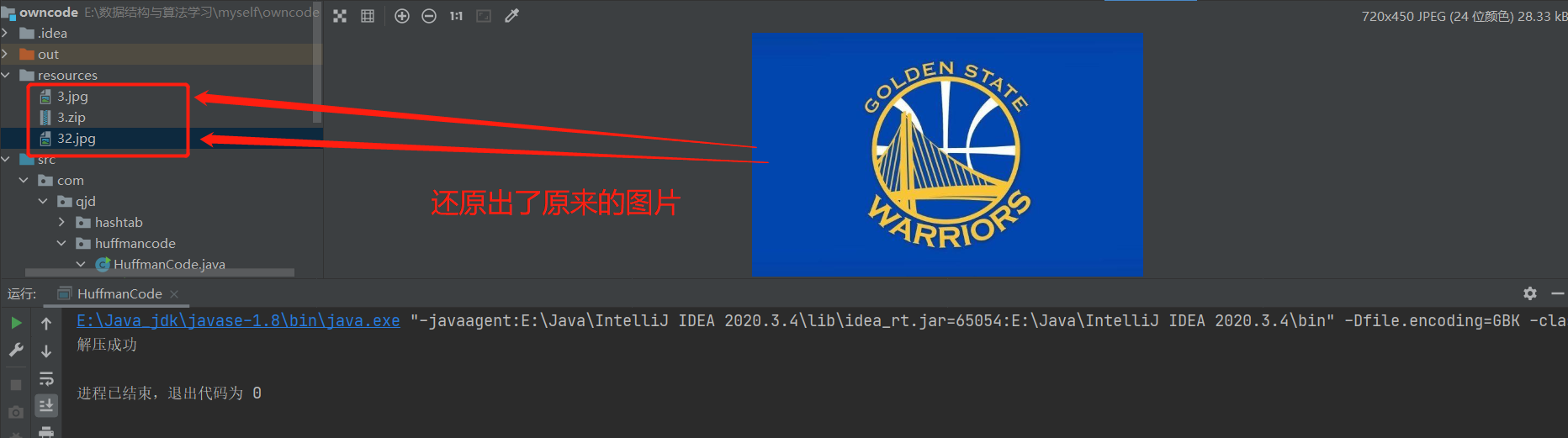
我们取文件夹中查看发现原始的图片和解压后的文件大小一样---->无损压缩
3.8、代码汇总
我们将赫夫曼编码所有的代码进行汇总
package com.qjd.huffmancode;
import java.io.*;
import java.util.*;
public class HuffmanCode {
public static void main(String[] args) {
/*
String content = "i like like like java do you like a java";
byte[] contentBytes = content.getBytes();
System.out.println("原始的content字符串长度为:"+contentBytes.length);//40
//压缩
byte[] huffmanCodesBytes = huffmanZip(contentBytes);
System.out.println("对content字符串压缩后的结果是:"+Arrays.toString(huffmanCodesBytes)+"长度为:"+huffmanCodesBytes.length);
//解压
byte[] sourceBytes = decode(huffmanCodes, huffmanCodesBytes);
System.out.println("(解压后)原来的字符串="+new String(sourceBytes)+"长度为:"+new String(sourceBytes).length());
*/
//测试压缩文件
// String srcFile = "E:\\数据结构与算法学习\\myself\\owncode\\resources\\3.jpg";
// String dstFile ="E:\\数据结构与算法学习\\myself\\owncode\\resources\\3.zip";
// zipFile(srcFile,dstFile);
// System.out.println("压缩文件成功");
//测试解压文件
String zipFile = "E:\\数据结构与算法学习\\myself\\owncode\\resources\\3.zip";
String dstFile = "E:\\数据结构与算法学习\\myself\\owncode\\resources\\32.jpg";
unZipFile(zipFile,dstFile);
System.out.println("解压成功");
}
//编写一个方法,完成对压缩文件的解压
/**
*
* @param zipFile 准备解压的文件
* @param dstFile 将文件解压到哪个路径
*/
public static void unZipFile(String zipFile, String dstFile) {
//定义文件输入流
InputStream is = null;
//定义一个对象输入流
ObjectInputStream ois = null;
//定义文件的输出流
OutputStream os = null;
try {
//创建文件输入流
is = new FileInputStream(zipFile);
//创建一个和 is关联的对象输入流
ois = new ObjectInputStream(is);
//读取byte数组 huffmanBytes
byte[] huffmanBytes = (byte[])ois.readObject();
//读取赫夫曼编码表
Map<Byte,String> huffmanCodes = (Map<Byte,String>)ois.readObject();
//解码
byte[] bytes = decode(huffmanCodes, huffmanBytes);
//将bytes 数组写入到目标文件
os = new FileOutputStream(dstFile);
//写数据到 dstFile 文件
os.write(bytes);
} catch (Exception e) {
System.out.println(e.getMessage());
} finally {
try {
os.close();
ois.close();
is.close();
} catch (Exception e2) {
System.out.println(e2.getMessage());
}
}
}
//编写方法,将一个文件进行压缩
/**
*
* @param srcFile 你传入的希望压缩的文件的全路径
* @param dstFile 我们压缩后将压缩文件放到哪个目录
*/
public static void zipFile(String srcFile, String dstFile) {
//创建输出流
OutputStream os = null;
ObjectOutputStream oos = null;
//创建文件的输入流
FileInputStream is = null;
try {
//创建文件的输入流
is = new FileInputStream(srcFile);
//创建一个和源文件大小一样的byte[]
byte[] b = new byte[is.available()];
//读取文件
is.read(b);
//直接对源文件压缩
byte[] huffmanBytes = huffmanZip(b);
//创建文件的输出流, 存放压缩文件
os = new FileOutputStream(dstFile);
//创建一个和文件输出流关联的ObjectOutputStream
oos = new ObjectOutputStream(os);
//把 赫夫曼编码后的字节数组写入压缩文件
oos.writeObject(huffmanBytes);
//这里我们以对象流的方式写入 赫夫曼编码,是为了以后我们恢复源文件时使用
//注意一定要把赫夫曼编码 写入压缩文件
oos.writeObject(huffmanCodes);
}catch (Exception e) {
System.out.println(e.getMessage());
}finally {
try {
is.close();
oos.close();
os.close();
}catch (Exception e) {
System.out.println(e.getMessage());
}
}
}
//完成数据的解压
//思路
//1. 将huffmanCodeBytes [-88, -65, -56, -65, -56, -65, -55, 77, -57, 6, -24, -14, -117, -4, -60, -90, 28]
// 重新先转成 赫夫曼编码对应的二进制的字符串 "1010100010111..."
//2. 赫夫曼编码对应的二进制的字符串 "1010100010111..." =》 对照 赫夫曼编码 =》 "i like like like java do you like a java"
/**
* 将一个byte 转成一个二进制的字符串, 这里需要利用二进制的原码,反码,补码
* @param b 传入的 byte
* @param flag 标志是否需要补高位如果是true ,表示需要补高位,如果是false表示不补, 如果是最后一个字节,无需补高位
* @return 是该b 对应的二进制的字符串,(注意是按补码返回)
*/
private static String byteToBitString(boolean flag, byte b) {
//使用变量保存 b
int temp = b; //将 b 转成 int
//如果是正数我们还存在补高位
if(flag) {
temp |= 256; //按位与 256 1 0000 0000 | 0000 0001 => 1 0000 0001
}
String str = Integer.toBinaryString(temp); //返回的是temp对应的二进制的补码
if(flag) {
return str.substring(str.length() - 8);
} else {
return str;
}
}
//编写一个方法,完成对压缩数据的解码
/**
*
* @param huffmanCodes 赫夫曼编码表 map(key = value)
* @param huffmanBytes 赫夫曼编码得到的字节数组
* @return 就是原来的字符串对应的数组
*/
private static byte[] decode(Map<Byte,String> huffmanCodes, byte[] huffmanBytes) {
//1. 先得到 huffmanBytes 对应的 二进制的字符串 , 形式 1010100010111...
StringBuilder stringBuilder = new StringBuilder();
//将byte数组转成二进制的字符串
for(int i = 0; i < huffmanBytes.length; i++) {
byte b = huffmanBytes[i];
//判断是不是最后一个字节
boolean flag = (i == huffmanBytes.length - 1);
stringBuilder.append(byteToBitString(!flag, b));
}
//把字符串按照指定的赫夫曼编码进行解码
//把赫夫曼编码表进行调换,因为反向查询 a->100 100->a
Map<String, Byte> map = new HashMap<String,Byte>();
for(Map.Entry<Byte, String> entry: huffmanCodes.entrySet()) {
map.put(entry.getValue(), entry.getKey());
//key = value 变成 value = key
}
//创建要给集合,存放byte
List<Byte> list = new ArrayList<>();
//i 可以理解成就是索引,扫描 stringBuilder
for(int i = 0; i < stringBuilder.length(); ) {
int count = 1; // 小的计数器
boolean flag = true;
Byte b = null;
while(flag) {
//1010100010111...
//递增的取出 key 1 (1,10,101...匹配)
String key = stringBuilder.substring(i, i+count);//i 不动,让count移动,指定匹配到一个字符
b = map.get(key);
if(b == null) {//说明没有匹配到
count++;
}else {
//匹配到
flag = false;
}
}
list.add(b);
i += count;//i 直接移动到 count
}
//当for循环结束后,我们list中就存放了所有的字符 "i like like like java do you like a java"
//把list 中的数据放入到byte[] 并返回
byte b[] = new byte[list.size()];
for(int i = 0;i < b.length; i++) {
b[i] = list.get(i);
}
return b;
}
//使用一个方法,将前面的方法封装起来,便于我们的调用
/**
* @param bytes 原始的字符串对应的字节数组
* @return 是经过 赫夫曼编码处理后的字节数组(压缩后的数组)
*/
private static byte[] huffmanZip(byte[] bytes){
List<Node> nodes = getNodes(bytes);
//根据nodes创建的赫夫曼树
Node huffmanTreeRoot = createHuffmanTree(nodes);
//生成对应的赫夫曼编码(根据赫夫曼树)
Map<Byte, String> huffmanCodes = getCodes(huffmanTreeRoot);
//根据生成的赫夫曼编码来对原始的字节数组进行压缩
byte[] huffmanCodeBytes = zip(bytes, huffmanCodes);
return huffmanCodeBytes;
}
//编写一个方法,将字符串对应的byte[] 数组,通过生成的赫夫曼编码表,返回一个赫夫曼编码 压缩后的byte[]
/**
*
* @param bytes 这是原始的字符串对应的 byte[]
* @param huffmanCodes 生成的赫夫曼编码map
* @return 返回赫夫曼编码处理后的 byte[]
* 举例: String content = "i like like like java do you like a java"; =》 byte[] contentBytes = content.getBytes();
* 返回的是 字符串 "1010100010111111110010001011111111001000101111111100100101001101110001110000011011101000111100101000101111111100110001001010011011100"
* => 对应的 byte[] huffmanCodeBytes ,即 8位对应一个 byte,放入到 huffmanCodeBytes
* huffmanCodeBytes[0] = 10101000(补码) => byte [推导 10101000=> 10101000 - 1 => 10100111(反码)=> 11011000(原码)= -88 ]
* huffmanCodeBytes[1] = -88
*/
private static byte[] zip(byte[] bytes, Map<Byte, String> huffmanCodes) {
//1.利用 huffmanCodes 将 bytes 转成 赫夫曼编码对应的字符串
StringBuilder stringBuilder = new StringBuilder();
//遍历bytes 数组
for(byte b: bytes) {
stringBuilder.append(huffmanCodes.get(b));
}
//System.out.println("测试 stringBuilder~~~=" + stringBuilder.toString());
//将 "1010100010111111110..." 转成 byte[]
//统计返回 byte[] huffmanCodeBytes 长度
//一句话 int len = (stringBuilder.length() + 7) / 8;
int len;
if(stringBuilder.length() % 8 == 0) {
len = stringBuilder.length() / 8;
} else {
len = stringBuilder.length() / 8 + 1;
}
//创建 存储压缩后的 byte数组
byte[] huffmanCodeBytes = new byte[len];
int index = 0;//记录是第几个byte
for (int i = 0; i < stringBuilder.length(); i += 8) { //因为是每8位对应一个byte,所以步长 +8
String strByte;
if(i+8 > stringBuilder.length()) {//不够8位
strByte = stringBuilder.substring(i);
}else{
strByte = stringBuilder.substring(i, i + 8);
}
//将strByte 转成一个byte,放入到 huffmanCodeBytes
huffmanCodeBytes[index] = (byte)Integer.parseInt(strByte, 2);
index++;
}
return huffmanCodeBytes;
}
//生成赫夫曼树对应的赫夫曼编码
//思路:
//1. 将赫夫曼编码表存放在 Map<Byte,String> 形式
// 生成的赫夫曼编码表{32(空格)=01, 97(a)=100, 100(...)=11000, 117=11001, 101=1110, 118=11011, 105=101, 121=11010, 106=0010, 107=1111, 108=000, 111=0011}
static Map<Byte, String> huffmanCodes = new HashMap<Byte,String>();
//2. 在生成赫夫曼编码表示,需要去拼接路径, 定义一个StringBuilder 存储某个叶子结点的路径
static StringBuilder stringBuilder = new StringBuilder();
//为了调用方便,我们重载 getCodes
private static Map<Byte, String> getCodes(Node root) {
if(root == null) {
return null;
}
//处理root的左子树
getCodes(root.left, "0", stringBuilder);
//处理root的右子树
getCodes(root.right, "1", stringBuilder);
return huffmanCodes;
}
/**
* 功能:将传入的node结点的所有叶子结点的赫夫曼编码得到,并放入到huffmanCodes集合
* @param node 传入结点
* @param code 路径: 左子结点是 0, 右子结点 1
* @param stringBuilder 用于拼接路径
*/
private static void getCodes(Node node,String code,StringBuilder stringBuilder){
StringBuilder stringBuilder2 = new StringBuilder(stringBuilder);
//将code加入到 stringBuilder2 (拼接路径)
stringBuilder2.append(code);
if (node != null){//如果node等于空,不处理
//判断当前node是叶子节点还是非叶子结点
if (node.data == null){//非叶子节点
//递归处理
//向左递归
getCodes(node.left, "0", stringBuilder2);
//向右递归
getCodes(node.right, "1", stringBuilder2);
}else {//进入到这里说明是叶子节点,找到了最后
huffmanCodes.put(node.data,stringBuilder2.toString());
}
}
}
//前序遍历的方法
public static void preOrder(Node root){
if (root != null){
root.preOrder();
}else {
System.out.println("赫夫曼树为空");
}
}
/**
*
* @param bytes 接收字节数组
* @return 返回的就是 List 形式 [Node[date=97 ,weight = 5], Node[]date=32,weight = 9]......],
*/
private static List<Node> getNodes(byte[] bytes){
//1.创建一个ArrayList
ArrayList<Node> nodes = new ArrayList<>();
//遍历bytes,存储每一个byte出现的次数=》map[key,value]
HashMap<Byte,Integer> counts = new HashMap<>();
for (byte b: bytes) {
Integer count = counts.get(b);
if (count == null){//Map还没有这个数据
counts.put(b,1);
}else {
counts.put(b,count+1);
}
}
//把每个键值对转成一个Node对象,并加入到nodes集合
//遍历map
for (Map.Entry<Byte,Integer> entry : counts.entrySet()){
nodes.add(new Node(entry.getKey(), entry.getValue()));
}
return nodes;
}
//通过list创建应的赫夫曼树
private static Node createHuffmanTree(List<Node> nodes){
while (nodes.size() > 1){
//排序,从小到大
Collections.sort(nodes);
//取出第一棵最小的二叉树左节点
Node leftNode = nodes.get(0);
//取出第二棵最小的二叉树右节点
Node rightNode = nodes.get(1);
//创建一棵新的二叉树,它的根节点没有data,只有权值
Node parent = new Node(null, leftNode.weight+ rightNode.weight);
parent.left = leftNode;
parent.right = rightNode;
//将已经处理的两棵二叉树从nodes删除
nodes.remove(leftNode);
nodes.remove(rightNode);
//将新的二叉树加入到nodes
nodes.add(parent);
}
//nodes 最后的节点就是赫夫曼树的根节点
return nodes.get(0);
}
}
//创建Node,带数据和权值
class Node implements Comparable<Node>{
Byte data;//存放数据本身 a===>97 ascii码
int weight;//权值,表示字符出现的次数
Node left;
Node right;
public Node(Byte data, int weight) {
this.data = data;
this.weight = weight;
}
@Override
public int compareTo(Node o) {
//从小到大排序
return this.weight-o.weight;
}
public String toString() {
return "Node [data = " + data + " weight=" + weight + "]";
}
//前序遍历
public void preOrder() {
System.out.println(this);
if(this.left != null) {
this.left.preOrder();
}
if(this.right != null) {
this.right.preOrder();
}
}
}
3.9、赫夫曼编码压缩注意事项
- 如果文件本身就是经过压缩处理的,那么使用赫夫曼编码再压缩效率不会有明显变化, 比如视频,ppt 等等文件
[举例:压缩一个 .ppt] - 赫夫曼编码是按字节来处理的,因此可以处理所有的文件(二进制文件、文本文件) [举例压一个.xml 文件]
- 如果一个文件中的内容,重复的数据不多,压缩效果也不会很明显.
4、二叉排序树(BST)
4.1、实际需求
给出一个数列 (7, 3, 10, 12, 5, 1, 9),要求能够高效的完成对数据的查询和添加
解决方案:
1、使用数组
数组未排序, 优点:直接在数组尾添加,速度快。 缺点:查找速度慢.
数组排序,优点:可以使用二分查找,查找速度快,缺点:为了保证数组有序,在添加新数据时,找到插入位置后,后面的数据需整体移动,速度慢。
2、使用链式存储-链表
不管链表是否有序,查找速度都慢,添加数据速度比数组快,不需要数据整体移动。
3、使用二叉排序树
4.2、二叉排序树简介
二叉排序树:
BST: (Binary Sort(Search) Tree), 对于二叉排序树的 任何一个非叶子节点,要求 左子节点的值比当前节点的值小, 右子节点的值比当前节点的值大。
特别说明:如果有相同的值,可以将该节点放在左子节点或右子节点
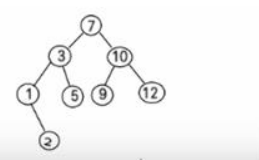
比如针对前面的数据 (7, 3, 10, 12, 5, 1, 9) ,对应的二叉排序树为:
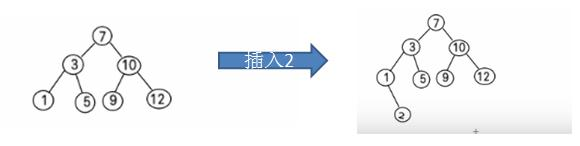
4.3、二叉排序树的创建与遍历
一个数组创建成对应的二叉排序树,并使用中序遍历二叉排序树,比如: 数组为 Array(7, 3, 10, 12, 5, 1, 9) , 创
建成对应的二叉排序树为 :

二叉排序树的创建与遍历代码
public class BinarySortTreeDemo {
public static void main(String[] args) {
int[] arr = {7,3,10,12,5,1,9};
BinarySortTree binarySortTree = new BinarySortTree();
//循环的添加节点到二叉排序树
for (int i = 0; i < arr.length; i++) {
binarySortTree.add(new Node(arr[i]));
}
//中序遍历二叉排序树
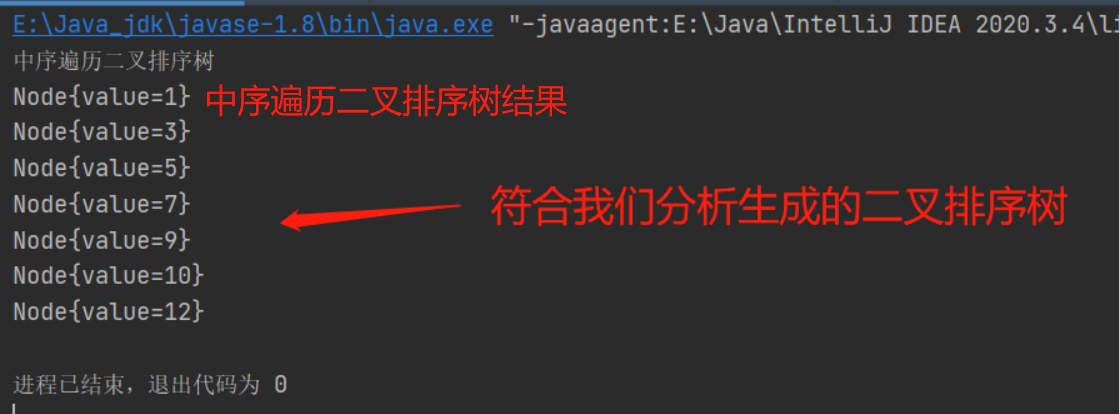
System.out.println("中序遍历二叉排序树");
binarySortTree.infixOrder();
}
}
//创建二叉排序树
class BinarySortTree{
private Node root;
//添加节点的方法
public void add(Node node){
if (root == null){
root = node;//如果root为空则直接让root指向node
}else {
root.add(node);
}
}
//中序遍历
public void infixOrder(){
if (root != null){
root.infixOrder();
}else {
System.out.println("二叉排序树为空,不能遍历");
}
}
}
//创建Node节点
class Node{
int value;
Node left;
Node right;
public Node(int value) {
this.value = value;
}
//添加节点的方法
//递归的形式添加节点,需要满足二叉排序树的要求
public void add(Node node){
if (node == null){
return;
}
//判断传入的节点的值,和当前子树根节点的值的关系
if (node.value<this.value){
//如果当前节点左子节点为空,直接将node给左节点
if (this.left == null){
this.left = node;
}else {//如果当前节点左子节点不为空,就递归的向左子树进行添加
this.left.add(node);
}
}else {//添加的节点的值大于当前节点的值
if (this.right == null){
this.right = node;
}else {
this.right.add(node);
}
}
}
//中序遍历的方法
public void infixOrder() {
if(this.left != null) {
this.left.infixOrder();
}
System.out.println(this);
if(this.right != null) {
this.right.infixOrder();
}
}
@Override
public String toString() {
return "Node{" +
"value=" + value +
'}';
}
}
结果:
4.4、二叉树的删除
二叉排序树的删除情况比较复杂,有下面三种情况需要考虑
-
点 删除叶子节点 (比如:2, 5, 9, 12)
-
删除点 只有一颗子树的节点 (比如:1)
-
删除 有两颗子树的节点. (比如:7, 3,10 )
思路分析
第一种情况:删除叶子节点 (比如:2, 5, 9, 12)
思路
(1) 需求先去找到要删除的结点 targetNode
(2) 找到targetNode 的 父结点parent
(3) 确定 targetNode 是 parent的左子结点 还是右子结点
(4) 根据前面的情况来对应删除
左子结点 parent.left = null
右子结点 parent.right = null;
第二种情况: 删除只有一颗子树的节点 比如1
思路
(1) 需求先去找到要删除的结点 targetNode
(2) 找到targetNode 的 父结点parent
(3) 确定targetNode 的子结点是左子结点还是右子结点
(4) targetNode 是parent的左子结点还是右子结点
(5) 如果targetNode 有左子结点
- 1 如果
targetNode是parent的左子结点
parent.left = targetNode.left;
5.2 如果targetNode是 parent 的右子结点
parent.right = targetNode.left;
(6) 如果targetNode 有右子结点
6.1 如果 targetNode 是 parent 的左子结点
parent.left = targetNode.right;
6.2 如果 targetNode 是parent的右子结点
parent.right = targetNode.right
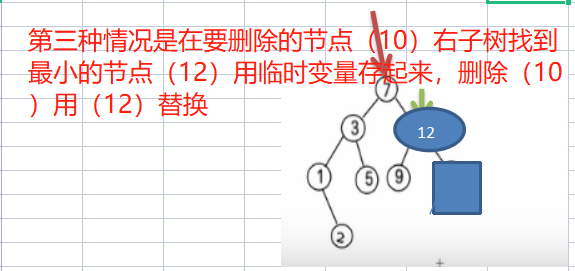
第三种情况 : 删除有两颗子树的节点. (比如:7, 3,10 )
思路
(1) 需求先去找到要删除的结点 targetNode
(2) 找到targetNode 的 父结点parent
(3) 从targetNode 的右子树找到最小的结点
(4) 用一个临时变量,将 最小结点的值保存 temp = 12
(5) 删除该最小结点
(6) targetNode.value = temp
代码实现
package com.qjd.binarysorttree;
public class BinarySortTreeDemo {
public static void main(String[] args) {
int[] arr = {7,3,10,12,5,1,9,2};
BinarySortTree binarySortTree = new BinarySortTree();
//循环的添加节点到二叉排序树
for (int i = 0; i < arr.length; i++) {
binarySortTree.add(new Node(arr[i]));
}
//中序遍历二叉排序树
System.out.println("中序遍历二叉排序树");
binarySortTree.infixOrder();
//测试删除节点
// binarySortTree.delNode(2);
// binarySortTree.delNode(5);
// binarySortTree.delNode(9);
// binarySortTree.delNode(12);
// binarySortTree.delNode(1);
binarySortTree.delNode(10);
System.out.println("删除节点后");
binarySortTree.infixOrder();
}
}
//创建二叉排序树
class BinarySortTree{
private Node root;
//添加节点的方法
public void add(Node node){
if (root == null){
root = node;//如果root为空则直接让root指向node
}else {
root.add(node);
}
}
//查找要删除的结点
public Node search(int value) {
if(root == null) {
return null;
} else {
return root.search(value);
}
}
//查找父结点
public Node searchParent(int value) {
if(root == null) {
return null;
} else {
return root.searchParent(value);
}
}
//编写方法:
//1. 返回的 以node 为根结点的二叉排序树的最小结点的值
//2. 删除node 为根结点的二叉排序树的最小结点
/**
*
* @param node 传入的结点(当做二叉排序树的根结点)
* @return 返回的 以node 为根结点的二叉排序树的最小结点的值
*/
public int delRightTreeMin(Node node) {
Node target = node;
//!!!这里是向右子树查找,但是因为是二叉排序树所以最小值一定在左子树上
while(target.left != null) {
target = target.left;
}
//这时 target就指向了最小结点
//删除最小结点
delNode(target.value);
return target.value;
}
//删除结点
public void delNode(int value) {
if(root == null) {
return;
}else {
//1.需要先去找到要删除的结点 targetNode
Node targetNode = search(value);
//如果没有找到要删除的结点
if(targetNode == null) {
return;
}
//如果我们发现当前这颗二叉排序树只有一个结点
if(root.left == null && root.right == null) {
root = null;
return;
}
//去找到targetNode的父结点
Node parent = searchParent(value);
//如果要删除的结点是叶子结点
if(targetNode.left == null && targetNode.right == null) {
//判断targetNode 是父结点的左子结点,还是右子结点
if(parent.left != null && parent.left.value == value) { //是左子结点
parent.left = null;
} else if (parent.right != null && parent.right.value == value) {//是右子结点
parent.right = null;
}
} else if (targetNode.left != null && targetNode.right != null) { //删除有两颗子树的节点
int minVal = delRightTreeMin(targetNode.right);//在右子树中查找最小值
targetNode.value = minVal;
} else { // 删除只有一颗子树的结点
//如果要删除的结点有左子结点
if(targetNode.left != null) {
if(parent != null) {
//如果 targetNode 是 parent 的左子结点
if(parent.left.value == value) {
parent.left = targetNode.left;
} else { // targetNode 是 parent 的右子结点
parent.right = targetNode.left;
}
} else {
root = targetNode.left;
}
} else { //如果要删除的结点有右子结点
if(parent != null) {
//如果 targetNode 是 parent 的左子结点
if(parent.left.value == value) {
parent.left = targetNode.right;
} else { //如果 targetNode 是 parent 的右子结点
parent.right = targetNode.right;
}
} else {
root = targetNode.right;
}
}
}
}
}
//中序遍历
public void infixOrder(){
if (root != null){
root.infixOrder();
}else {
System.out.println("二叉排序树为空,不能遍历");
}
}
}
//创建Node节点
class Node{
int value;
Node left;
Node right;
public Node(int value) {
this.value = value;
}
//查找要删除的节点
/**
*
* @param value 希望删除的结点的值
* @return 如果找到返回该结点,否则返回null
*/
public Node search(int value) {
if(value == this.value) { //找到就是该结点
return this;
} else if(value < this.value) {//如果查找的值小于当前结点,向左子树递归查找
//如果左子结点为空
if(this.left == null) {
return null;
}
return this.left.search(value);
} else { //如果查找的值不小于当前结点,向右子树递归查找
if(this.right == null) {
return null;
}
return this.right.search(value);
}
}
//查找要删除结点的父结点
/**
*
* @param value 要找到的结点的值
* @return 返回的是要删除的结点的父结点,如果没有就返回null
*/
public Node searchParent(int value) {
//如果当前结点就是要删除的结点的父结点,就返回
if((this.left != null && this.left.value == value) ||
(this.right != null && this.right.value == value)) {
return this;
} else {
//如果查找的值小于当前结点的值, 并且当前结点的左子结点不为空
if(value < this.value && this.left != null) {
return this.left.searchParent(value); //向左子树递归查找
} else if (value >= this.value && this.right != null) {
return this.right.searchParent(value); //向右子树递归查找
} else {
return null; // 没有找到父结点
}
}
}
//添加节点的方法
//递归的形式添加节点,需要满足二叉排序树的要求
public void add(Node node){
if (node == null){
return;
}
//判断传入的节点的值,和当前子树根节点的值的关系
if (node.value<this.value){
//如果当前节点左子节点为空,直接将node给左节点
if (this.left == null){
this.left = node;
}else {//如果当前节点左子节点不为空,就递归的向左子树进行添加
this.left.add(node);
}
}else {//添加的节点的值大于当前节点的值
if (this.right == null){
this.right = node;
}else {
this.right.add(node);
}
}
}
//中序遍历的方法
public void infixOrder() {
if(this.left != null) {
this.left.infixOrder();
}
System.out.println(this);
if(this.right != null) {
this.right.infixOrder();
}
}
@Override
public String toString() {
return "Node{" +
"value=" + value +
'}';
}
}
结果:
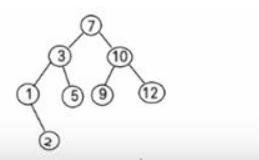
1、删除叶子节点2、5、9
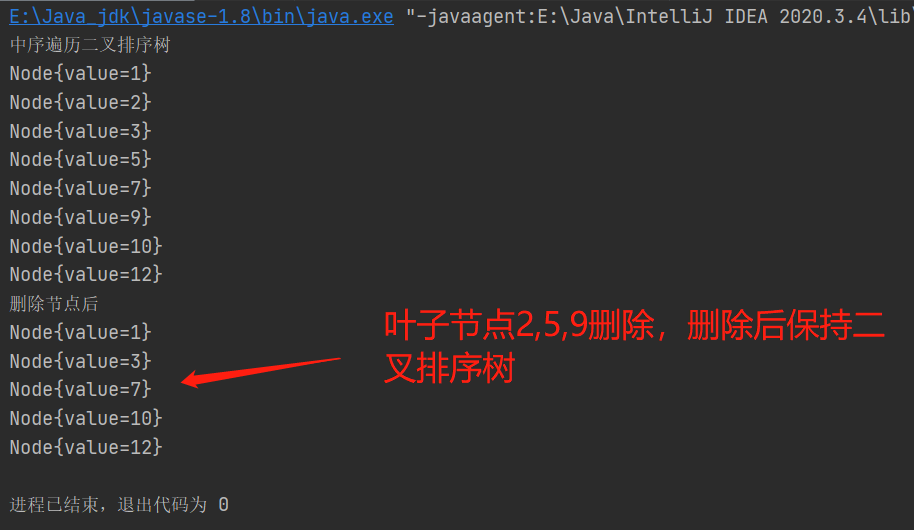
2、删除只有一颗子树的节点 1
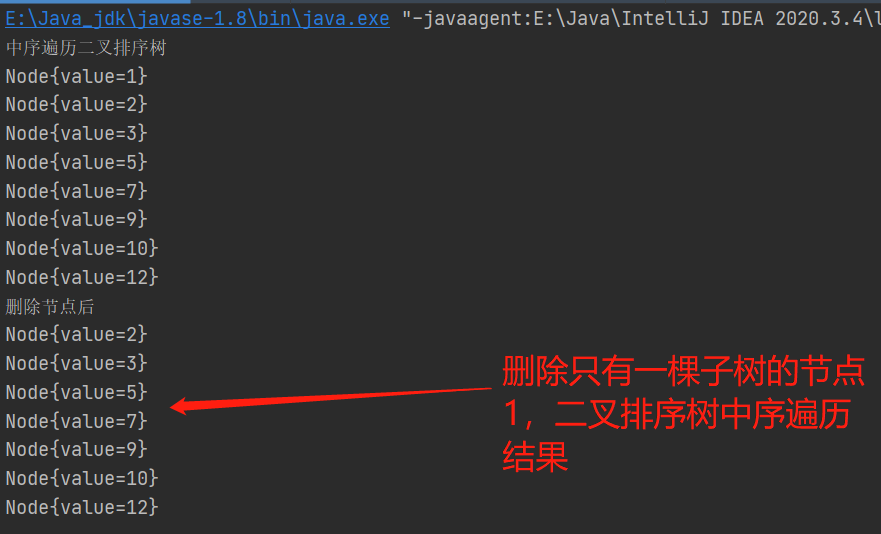
3、删除有两颗子树的节点10
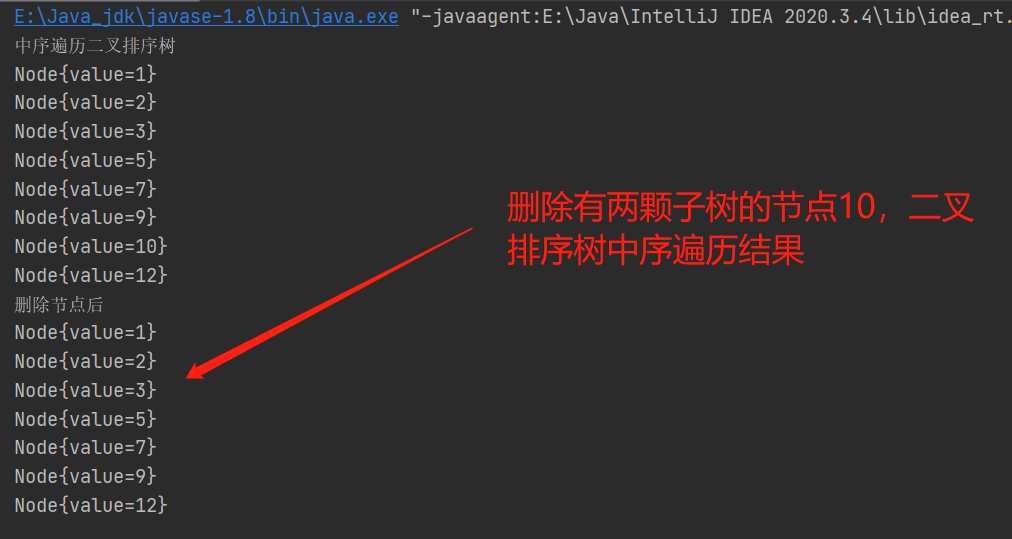
5、平衡二叉树(AVL)
5.1、实际案例
给出一个数列{1,2,3,4,5,6},要求创建一颗二叉排序树(BST), 并分析问题所在.
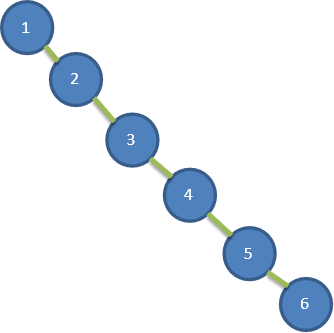
左边 BST 存在的问题分析:
- 左子树全部为空,从形式上看,更像一个单链表.
- 插入速度没有影响
- 查询速度明显降低(因为需要依次比较), 不能发挥 BST的优势,因为每次还需要比较左子树,其查询速度比单链表还慢
- 解决方案-平衡二叉树(AVL)
5.2、平衡二叉树简介
- 平衡二叉树也叫平衡 二叉搜索树(Self-balancing binary search tree)又被称为 AVL 树, 可以保证查询效率较高。
- 具有以下特点:它是一 一 棵空树或 它的左右两个子树的高度差的绝对值不超过 1,并且 左右两个子树都是一棵
平衡二叉树。平衡二叉树的常用实现方法有红黑树、AVL、替罪羊树、Treap、伸展树等。 - 举例说明, 看看下面哪些 AVL 树, 为什么?
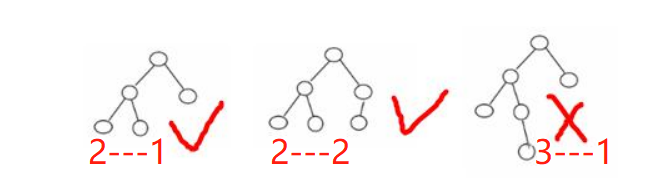
5.3、构建平衡二叉树
5.3.1、左旋转
1、要求: 给出一个数列,创建出对应的平衡二叉树.数列 {4,3,6,5,7,8}
2、思路分析

5.3.2、右旋转
1、要求: 给出一个数列,创建出对应的平衡二叉树.数列 {10,12, 8, 9, 7, 6}
2、思路分析

5.3.3、双旋转
前面的两个数列,进行单旋转(即一次旋转)就可以将非平衡二叉树转成平衡二叉树,但是在某些情况下,单旋转
不能完成平衡二叉树的转换。比如数列
int[] arr = { 10, 11, 7, 6, 8, 9 }; 运行原来的代码可以看到,并没有转成 AVL 树.
int[] arr = {2,1,6,5,7,3}; 运行原来的代码可以看到,并没有转成 AVL 树
1、问题分析
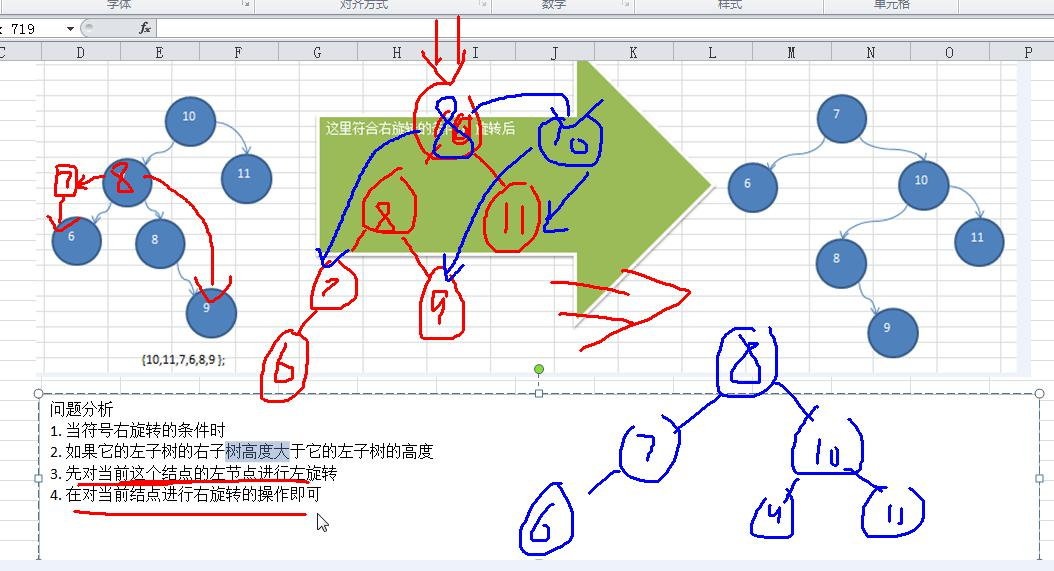
2、思路分析
- 当符号右旋转的条件时
- 如果它的左子树的右子树高度大于它的左子树的高度
- 先对当前这个结点的左节点进行左旋转
- 在对当前结点进行右旋转的操作即可
5.3.4、整体代码实现
public class AvlTreeDemo {
public static void main(String[] args) {
//int[] arr = {4,3,6,5,7,8};
//int[] arr = { 10, 12, 8, 9, 7, 6 };
int[] arr = { 10, 11, 7, 6, 8, 9 };
//创建一个 AVLTree对象
AVLTree avlTree = new AVLTree();
//添加结点
for(int i=0; i < arr.length; i++) {
avlTree.add(new Node(arr[i]));
}
//遍历
System.out.println("中序遍历");
avlTree.infixOrder();
System.out.println("在平衡处理后···");
System.out.println("树的高度=" + avlTree.getRoot().height()); //3
System.out.println("树的左子树高度=" + avlTree.getRoot().leftHeight()); // 2
System.out.println("树的右子树高度=" + avlTree.getRoot().rightHeight()); // 2
System.out.println("当前的根结点=" + avlTree.getRoot());//8
}
}
// 创建AVLTree
class AVLTree {
private Node root;
public Node getRoot() {
return root;
}
// 查找要删除的结点
public Node search(int value) {
if (root == null) {
return null;
} else {
return root.search(value);
}
}
// 查找父结点
public Node searchParent(int value) {
if (root == null) {
return null;
} else {
return root.searchParent(value);
}
}
// 编写方法:
// 1. 返回的 以node 为根结点的二叉排序树的最小结点的值
// 2. 删除node 为根结点的二叉排序树的最小结点
/**
*
* @param node
* 传入的结点(当做二叉排序树的根结点)
* @return 返回的 以node 为根结点的二叉排序树的最小结点的值
*/
public int delRightTreeMin(Node node) {
Node target = node;
// 循环的查找左子节点,就会找到最小值
while (target.left != null) {
target = target.left;
}
// 这时 target就指向了最小结点
// 删除最小结点
delNode(target.value);
return target.value;
}
// 删除结点
public void delNode(int value) {
if (root == null) {
return;
} else {
// 1.需求先去找到要删除的结点 targetNode
Node targetNode = search(value);
// 如果没有找到要删除的结点
if (targetNode == null) {
return;
}
// 如果我们发现当前这颗二叉排序树只有一个结点
if (root.left == null && root.right == null) {
root = null;
return;
}
// 去找到targetNode的父结点
Node parent = searchParent(value);
// 如果要删除的结点是叶子结点
if (targetNode.left == null && targetNode.right == null) {
// 判断targetNode 是父结点的左子结点,还是右子结点
if (parent.left != null && parent.left.value == value) { // 是左子结点
parent.left = null;
} else if (parent.right != null && parent.right.value == value) {// 是由子结点
parent.right = null;
}
} else if (targetNode.left != null && targetNode.right != null) { // 删除有两颗子树的节点
int minVal = delRightTreeMin(targetNode.right);
targetNode.value = minVal;
} else { // 删除只有一颗子树的结点
// 如果要删除的结点有左子结点
if (targetNode.left != null) {
if (parent != null) {
// 如果 targetNode 是 parent 的左子结点
if (parent.left.value == value) {
parent.left = targetNode.left;
} else { // targetNode 是 parent 的右子结点
parent.right = targetNode.left;
}
} else {
root = targetNode.left;
}
} else { // 如果要删除的结点有右子结点
if (parent != null) {
// 如果 targetNode 是 parent 的左子结点
if (parent.left.value == value) {
parent.left = targetNode.right;
} else { // 如果 targetNode 是 parent 的右子结点
parent.right = targetNode.right;
}
} else {
root = targetNode.right;
}
}
}
}
}
// 添加结点的方法
public void add(Node node) {
if (root == null) {
root = node;// 如果root为空则直接让root指向node
} else {
root.add(node);
}
}
// 中序遍历
public void infixOrder() {
if (root != null) {
root.infixOrder();
} else {
System.out.println("二叉排序树为空,不能遍历");
}
}
}
// 创建Node结点
class Node {
int value;
Node left;
Node right;
public Node(int value) {
this.value = value;
}
// 返回左子树的高度
public int leftHeight() {
if (left == null) {
return 0;
}
return left.height();
}
// 返回右子树的高度
public int rightHeight() {
if (right == null) {
return 0;
}
return right.height();
}
// 返回 以该结点为根结点的树的高度
public int height() {
return Math.max(left == null ? 0 : left.height(), right == null ? 0 : right.height()) + 1;
}
//左旋转方法
private void leftRotate() {
//创建新的结点,以当前根结点的值
Node newNode = new Node(value);
//把新的结点的左子树设置成当前结点的左子树
newNode.left = left;
//把新的结点的右子树设置成带你过去结点的右子树的左子树
newNode.right = right.left;
//把当前结点的值替换成右子结点的值
value = right.value;
//把当前结点的右子树设置成当前结点右子树的右子树
right = right.right;
//把当前结点的左子树(左子结点)设置成新的结点
left = newNode;
}
//右旋转
private void rightRotate() {
Node newNode = new Node(value);
newNode.right = right;
newNode.left = left.right;
value = left.value;
left = left.left;
right = newNode;
}
// 查找要删除的结点
/**
*
* @param value
* 希望删除的结点的值
* @return 如果找到返回该结点,否则返回null
*/
public Node search(int value) {
if (value == this.value) { // 找到就是该结点
return this;
} else if (value < this.value) {// 如果查找的值小于当前结点,向左子树递归查找
// 如果左子结点为空
if (this.left == null) {
return null;
}
return this.left.search(value);
} else { // 如果查找的值不小于当前结点,向右子树递归查找
if (this.right == null) {
return null;
}
return this.right.search(value);
}
}
// 查找要删除结点的父结点
/**
*
* @param value
* 要找到的结点的值
* @return 返回的是要删除的结点的父结点,如果没有就返回null
*/
public Node searchParent(int value) {
// 如果当前结点就是要删除的结点的父结点,就返回
if ((this.left != null && this.left.value == value) || (this.right != null && this.right.value == value)) {
return this;
} else {
// 如果查找的值小于当前结点的值, 并且当前结点的左子结点不为空
if (value < this.value && this.left != null) {
return this.left.searchParent(value); // 向左子树递归查找
} else if (value >= this.value && this.right != null) {
return this.right.searchParent(value); // 向右子树递归查找
} else {
return null; // 没有找到父结点
}
}
}
@Override
public String toString() {
return "Node [value=" + value + "]";
}
// 添加结点的方法
// 递归的形式添加结点,注意需要满足二叉排序树的要求
public void add(Node node) {
if (node == null) {
return;
}
// 判断传入的结点的值,和当前子树的根结点的值关系
if (node.value < this.value) {
// 如果当前结点左子结点为null
if (this.left == null) {
this.left = node;
} else {
// 递归的向左子树添加
this.left.add(node);
}
} else { // 添加的结点的值大于 当前结点的值
if (this.right == null) {
this.right = node;
} else {
// 递归的向右子树添加
this.right.add(node);
}
}
//当添加完一个结点后,如果: (右子树的高度-左子树的高度) > 1 , 左旋转
if(rightHeight() - leftHeight() > 1) {
//如果它的右子树的左子树的高度大于它的右子树的右子树的高度
if(right != null && right.leftHeight() > right.rightHeight()) {
//先对右子结点进行右旋转
right.rightRotate();
//然后在对当前结点进行左旋转
leftRotate(); //左旋转..
} else {
//直接进行左旋转即可
leftRotate();
}
return ; //必须要!!!
}
//当添加完一个结点后,如果 (左子树的高度 - 右子树的高度) > 1, 右旋转
if(leftHeight() - rightHeight() > 1) {
//如果它的左子树的右子树高度大于它的左子树的高度
if(left != null && left.rightHeight() > left.leftHeight()) {
//先对当前结点的左结点(左子树)->左旋转
left.leftRotate();
//再对当前结点进行右旋转
rightRotate();
} else {
//直接进行右旋转即可
rightRotate();
}
}
}
// 中序遍历
public void infixOrder() {
if (this.left != null) {
this.left.infixOrder();
}
System.out.println(this);
if (this.right != null) {
this.right.infixOrder();
}
}
}
测试结果:
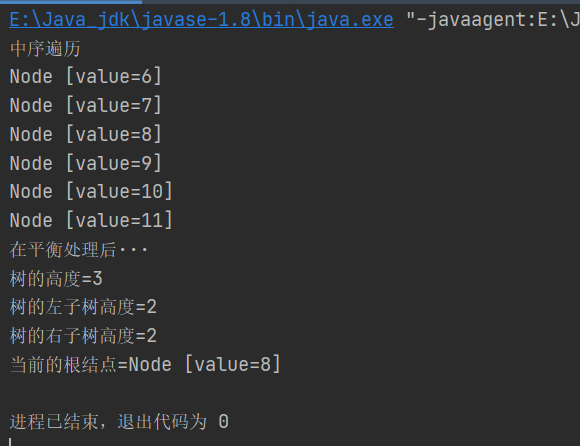
到这里关于树结构的实际应用的内容就结束了,关于树结构的具体应用像赫夫曼编码,二叉排序树等代码比较复杂,
大家重点要根据思路图解来分析解题过程,代码的具体实现要尽量理解,
最后希望这篇文章对大家有所帮助(◍•͈⌔•͈◍)



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· 阿里巴巴 QwQ-32B真的超越了 DeepSeek R-1吗?
· 【译】Visual Studio 中新的强大生产力特性
· 【设计模式】告别冗长if-else语句:使用策略模式优化代码结构
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义