数据结构与算法【Java】06---查找算法总结
前言
数据 data 结构(structure)是一门 研究组织数据方式的学科,有了编程语言也就有了数据结构.学好数据结构才可以编写出更加漂亮,更加有效率的代码。
- 要学习好数据结构就要多多考虑如何将生活中遇到的问题,用程序去实现解决.
- 程序 = 数据结构 + 算法
- 数据结构是算法的基础, 换言之,想要学好算法,需要把数据结构学到位
我会用数据结构与算法【Java】这一系列的博客记录自己的学习过程,如有遗留和错误欢迎大家提出,我会第一时间改正!!!
注:数据结构与算法【Java】这一系列的博客参考于B站尚硅谷的视频,文章仅用于学习交流,视频原地址为【尚硅谷】数据结构与算法(Java数据结构与算法),大家记得一键三连哦~
上一篇文章数据结构与算法【Java】05---排序算法总结
接下来进入正题!
数据结构与算法【Java】06---查找算法总结
1、查找算法简介
1.1、查找的定义
根据给定的某个值,在查找表中确定一个其关键字等于给定值的数据元素(或记录)。
1.2、查找算法分类
1)静态查找和动态查找
注:静态或者动态都是针对查找表而言的。动态表指查找表中有删除和插入操作的表。
2)无序查找和有序查找
无序查找:被查找数列有序无序均可;
有序查找:被查找数列必须为有序数列
平均查找长度(Average Search Length,ASL):需和指定key进行比较的关键字的个数的期望值,称为查找算法在查找成功时的平均查找长度。
对于含有n个数据元素的查找表,查找成功的平均查找长度为:ASL = Pi*Ci的和。
Pi:查找表中第i个数据元素的概率。
Ci:找到第i个数据元素时已经比较过的次数。
1.3、常用查找算法
- 顺序(线性)查找
- 二分查找/折半查找
- 插值查找
- 斐波那契查找
- 分块查找
- 哈希查找
- 树表查找
下面我们来详细的了解一下这七大查找算法!
2、线性查找算法
2.1、线性查找简介
- 线性查找也称顺序查找,通过遍历线性表来查找需要的值,直接遍历数组,判断元素是否相等即可,属无序查找算法
- 如果成功则返回地址,反之给予错误反馈
2.2、线性查找代码实现
要求:
有一个数列:{1,9,11,-1,34,89} ,判断数列中是否包含某一个给出的值
如果找到了,就提示找到,并给出下标值,如果没有找到给出反馈
线性查找代码
public class SeqSearch {
public static void main(String[] args) {
int arr[] = {1,9,11,-1,34,89};//没有顺序的数组
int index = seqSearch(arr,11);
if (index == -1){
System.out.println("没有查找到");
}else {
System.out.println("找到了要查找的值,下标为="+index);
}
}
/**
* 这里我们实现的线性查找是找到一个满足条件的值,就返回
* @param arr 没有顺序的数组
* @param value 想要查找的值
* @return
*/
public static int seqSearch(int [] arr,int value){
//线性查找是逐一比对,发现有相同值,就返回下标
for (int i = 0; i < arr.length; i++) {
if (arr[i] == value){
return i;
}
}
return -1;
}
}
这里的代码只实现了,查找相匹配的第一个元素的下标,如果找到所有元素可以定义一个集合,将return i;改成向集合中添加元素即可。
结果:
(1)seqSearch(arr,11);在数组中查找11
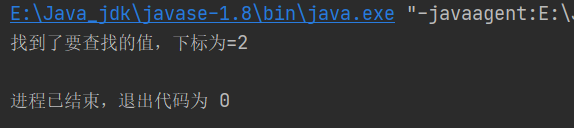
(2)seqSearch(arr,123);在数组中查找123
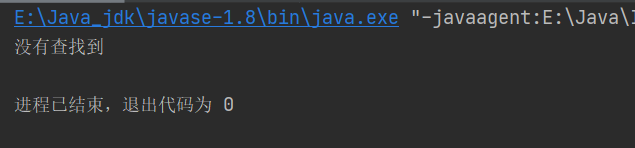
2.3、线性查找分析
- 时间复杂度:O(n)
- 线性查找 适合 顺序存储 || 链接存储 的线性表
3、二分查找算法
3.1、二分查找简介
二分查找也叫折半查找,前提是需要有序表顺序存储,属有序查找算法
顾名思义,通过将有序表折半查询
3.2、二分查找代码实现
思路分析
二分查找的思路是找到数组的中间下标,将待查找元素和中间下标对应值比较大小,大的话往数组右边查找,小的话往数组左边查找,直到找到为止,返回中间下标对应的元素值即可。
步骤:
1、首先确定该数组的中间的下标mid = (left + right) / 2
2、然后让需要查找的数 findVal 和 arr[mid] 比较
-
findVal>arr[mid], 说明你要查找的数在mid的右边, 因此需要递归的向右查找 -
findVal<arr[mid], 说明你要查找的数在mid的左边, 因此需要递归的向左查找 -
findVal==arr[mid]说明找到,就返回
什么时候我们需要结束递归?
- 找到就结束递归
- 递归完整个数组,仍然没有找到
findVal,也需要结束递归 ,即 当left > right就需要退出
代码实现
1、基本功能实现(没有重复的数据)
//注意:使用二分查找的前提是有序的
public class BinarySearch {
public static void main(String[] args) {
int arr[] = {1,8,10,89,1000,1234};
int resIndex = binarySearch(arr,0,arr.length-1,1000);
System.out.println("resIndex="+resIndex);
}
//二分查找算法
/**
*
* @param arr
* 数组
* @param left
* 左边的索引
* @param right
* 右边的索引
* @param findVal
* 要查找的值
* @return 如果找到就返回下标,如果没有找到,就返回 -1
*/
public static int binarySearch(int [] arr,int left,int right,int findVal){
// 当 left > right 时,说明递归整个数组,但是没有找到
if (left > right) {
return -1;
}
int mid = (left+right)/2;
int midVal = arr[mid];
if (findVal > midVal){//向右递归
return binarySearch(arr,mid+1,right,findVal);
}else if(findVal < midVal){//向左递归
return binarySearch(arr,left,mid-1,findVal);
}else {
return mid;
}
}
}
结果:
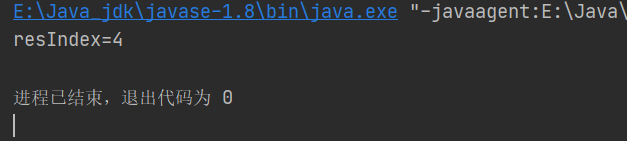
- 查找1000
binarySearch(arr,0,arr.length-1,1000);(可以查找到)
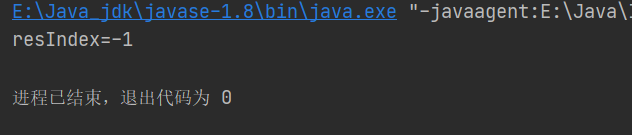
- 查找9999
binarySearch(arr,0,arr.length-1,9999);(可以不到,返回-1)
2、二分查找功能完善(查找数组中重复的数据)
//注意:使用二分查找的前提是有序的
public class BinarySearch {
public static void main(String[] args) {
int arr[] = {1,8,10,89,1000,1000,1000,1000,1000,1234};
ArrayList list = binarySearch2(arr, 0, arr.length - 1, 1000);
System.out.println("list="+list);
}
//功能完善
/**
* {1,8, 10, 89, 1000, 1000,1234} 当一个有序数组中,
* 有多个相同的数值时,如何将所有的数值都查找到,比如这里的 1000?
*
* 思路分析
* 1. 在找到mid 索引值,不要马上返回
* 2. 向mid 索引值的左边扫描,将所有满足 1000, 的元素的下标,加入到集合ArrayList
* 3. 向mid 索引值的右边扫描,将所有满足 1000, 的元素的下标,加入到集合ArrayList
* 4. 将Arraylist返回
*/
public static ArrayList binarySearch2(int [] arr, int left, int right, int findVal){
// 当 left > right 时,说明递归整个数组,但是没有找到,返回一个空的集合
if (left > right) {
return new ArrayList<Integer>();
}
int mid = (left+right)/2;
int midVal = arr[mid];
if (findVal > midVal){//向右递归
return binarySearch2(arr,mid+1,right,findVal);
}else if(findVal < midVal){//向左递归
return binarySearch2(arr,left,mid-1,findVal);
}else {
ArrayList<Integer> resIndexList = new ArrayList<>();
//向mid 索引值的左边扫描,将所有满足 1000, 的元素的下标,加入到集合ArrayList
int temp = mid - 1;
while (true){
if (temp < 0 || arr[temp] != findVal){//向左扫描完毕并退出
break;
}
//否则就temp放入到resIndexList
resIndexList.add(temp);
temp -= 1;//temp左移
}
resIndexList.add(mid);//不要忘了把中间的值加入
//向mid 索引值的右边扫描,将所有满足 1000, 的元素的下标,加入到集合ArrayList
temp = mid + 1;
while (true){
if (temp > arr.length - 1 || arr[temp] != findVal){//向右扫描完毕并退出
break;
}
//否则就temp放入到resIndexList
resIndexList.add(temp);
temp += 1;//temp右移
}
return resIndexList;
}
}
}
结果:这里直接将两个方法进行同时输出,方便比对
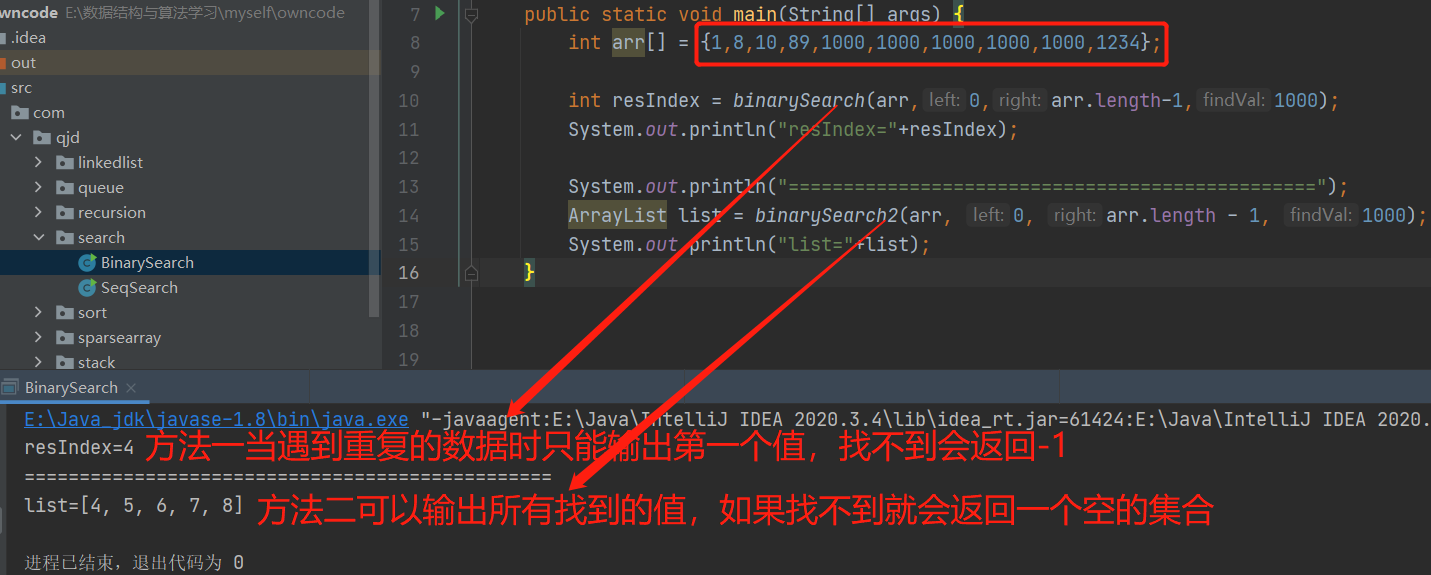
注意:使用第二种方法查找重复的数据,因为二分查找的前提是有序的,所以查找重复数据查出来的索引必定是连续的
3.3、二分查找分析
我们来看一张二分查找与遍历查找的效率对比图(图片来源于网络):
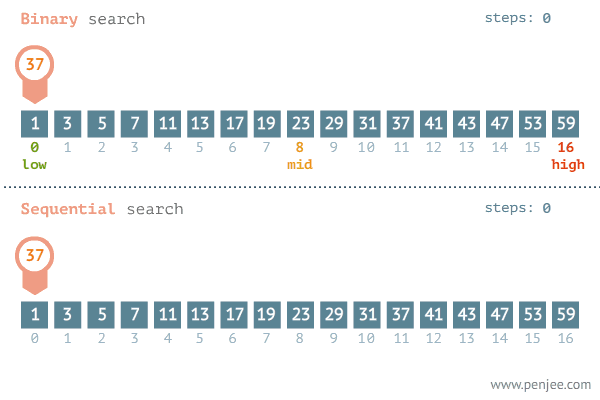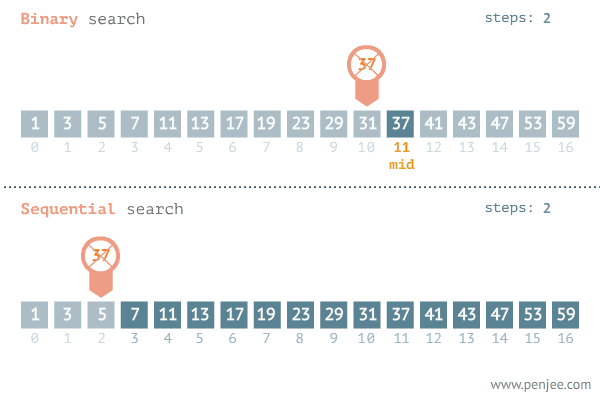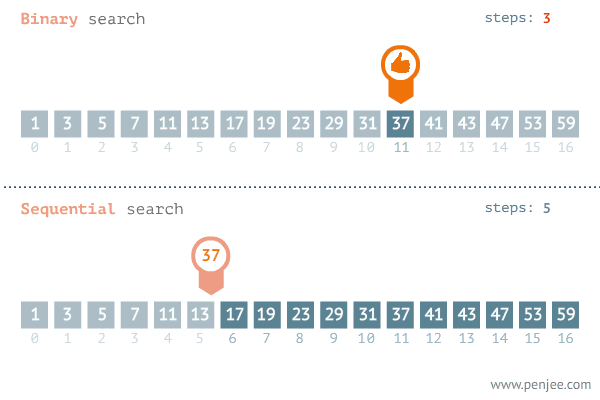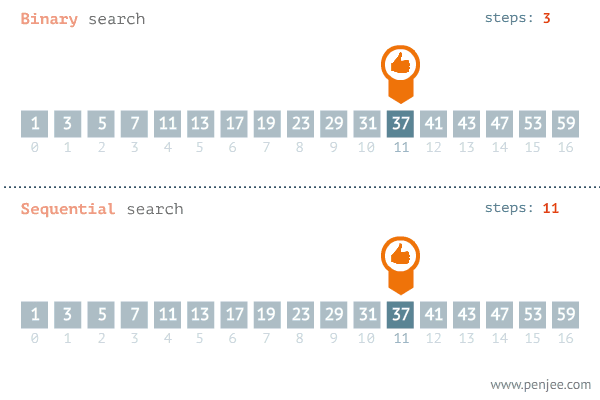
从图中可以看出二分查找用了三步就找到了查找值,而遍历则用了11步才找到查找值,二分查找的效率非常高。但是二分查找的局限性非常大。那二分查找有哪些局限性呢?
局限性:
-
二分查找依赖数组结构
二分查找需要利用下标随机访问元素,如果我们想使用链表等其他数据结构则无法实现二分查找。
-
二分查找针对的是有序数据
二分查找需要的数据必须是有序的。如果数据没有序,我们需要先排序,排序的时间复杂度最低是 O(nlogn)。所以,如果我们针对的是一组静态的数据,没有频繁地插入、删除,我们可以进行一次排序,多次二分查找。这样排序的成本可被均摊,二分查找的边际成本就会比较低。
但是,如果我们的数据集合有频繁的插入和删除操作,要想用二分查找,要么每次插入、删除操作之后保证数据仍然有序,要么在每 次二分查找之前都先进行排序。针对这种动态数据集合,无论哪种方法,维护有序的成本都是很高的。
所以,二分查找只能用在插入、删除操作不频繁,一次排序多次查找的场景中。针对动态变化的数据集合,二分查找将不再适用
- 数据量太小不适合二分查找
如果要处理的数据量很小,完全没有必要用二分查找,顺序遍历就足够了。比如我们在一个大小为 10 的数组中查找一个元素,不管 用二分查找还是顺序遍历,查找速度都差不多,只有数据量比较大的时候,二分查找的优势才会比较明显。
-
数据量太大不适合二分查找
二分查找底层依赖的是数组,数组需要的是一段连续的存储空间,所以我们的数据比较大时,比如1GB,这时候可能不太适合使用二分查找,因为我们的内存都是离散的,可能电脑没有这么多的内存。
小结:
-
时间复杂度:O(log2 n)
-
二分查找 只适合静态操作,每次数据的变动都将带来不少的工作量
4、插值查找算法
4.1、插值查找简介
插值查找原理介绍
-
插值查找基于二分查找算法,主要将查找点的选择改进为自适应选择;当然,差值查找也属于有序查找
-
二分查找主要将有序线性表折半,但当数据在远离中心位置时便会浪费很多资源,我们可以通过预估 key 在 Linear Table 中的大概位置来实现自适应
-
将折半查找中的求
mid索引的公式 ,low表示左边索引left,high表示右边索引right,key就是前面的findVal

-
int mid = low + (high - low) * (key - arr[low]) / (arr[high] - arr[low]) ;
对应前面的代码公式:
int mid = left + (right – left) * (findVal – arr[left]) / (arr[right] – arr[left]) -
举例说明

4.2、插值查找代码实现
public class InsertValueSearch {
public static void main(String[] args) {
//设置一个1~100的数组
int [] arr = new int[100];
for (int i = 0; i < 100; i++) {
arr[i] = i + 1;
}
//System.out.println(Arrays.toString(arr));
int index = insertValueSearch(arr, 0, arr.length - 1, 100);
System.out.println("要查找值的下标是:"+index);
}
//插值查找
//说明:插值查找算法,也要求数组是有序的
/**
*
* @param arr 数组
* @param left 左边索引
* @param right 右边索引
* @param findVal 查找值
* @return 如果找到,就返回对应的下标,如果没有找到,返回-1
*/
public static int insertValueSearch(int [] arr,int left,int right,int findVal){
System.out.println("插值查找次数~~");
//注意:findVal < arr[0] 和 findVal > arr[arr.length - 1] 必须需要
//否则我们得到的 mid 可能越界
if (left > right || findVal < arr[0] || findVal > arr[arr.length-1]){
return -1;
}
//求出mid
int mid = left + (right - left) * (findVal - arr[left]) / (arr[right] - arr[left]);
int midVal = arr[mid];
if (findVal > midVal){//大于标准值,说明应该向右边进行递归
return insertValueSearch(arr, mid+1, right, findVal);
}else if (findVal < midVal){//小于标准值,说明应该向左边进行递归
return insertValueSearch(arr, left, mid -1, findVal);
}else {
return mid;//找到值并返回
}
}
}
结果:
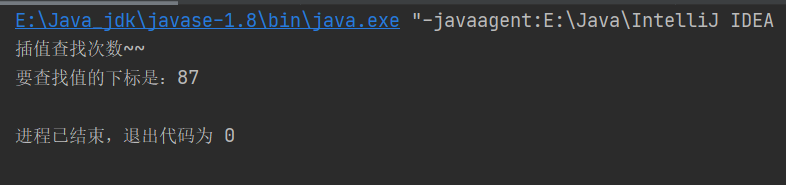
(1)在0~100的数组中查找一个指定的数据
int index = insertValueSearch(arr, 0, arr.length - 1, 88);
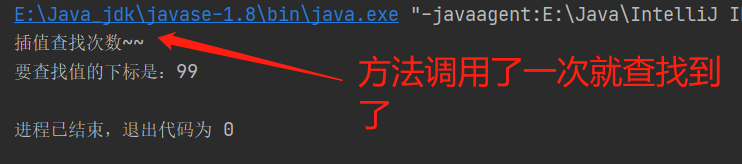
(2)查找100
int index = insertValueSearch(arr, 0, arr.length - 1, 100);
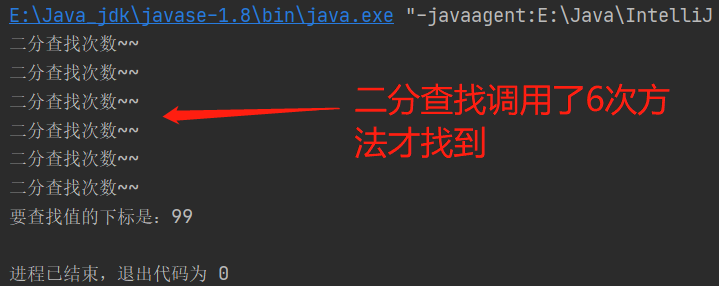
(3)比对二分查找(同样查找100)
int index = binarySearch(arr, 0, arr.length, 100);
4.3、插值查找分析
- 时间复杂度:
O(log(2)(log(2)n))--->log以2为底的(log以2为底的n的对数)的对数 - 对于数据量较大,关键字分布比较均匀的查找表来说,采用插值查找, 速度较快.
- 关键字分布不均匀的情况下,该方法不一定比折半查找要好
5、斐波那契查找算法
5.1、斐波那契查找简介
1、斐波那契查找又叫做黄金分割法查找, 它也是二分查找的一种提升算法,通过运用黄金比例的概念在有序数列中选择查找点进行查找,提高查找效率。同样地,斐波那契查找也属于一种有序查找算法
2、黄金分割点是指把一条线段分割为两部分,其中一部分与全长之比等于另一部分与这部分之比,比值近似0.618
由于按此比例设计的造型十分美丽,因此称为黄金分割,也称为中外比。这是一个神奇的数字,会带来意向不到的效果
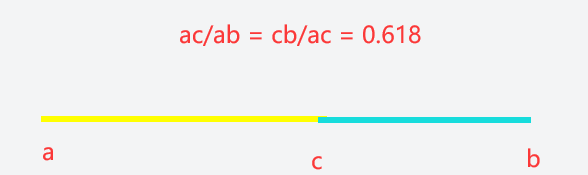
3、斐波那契数列
斐波那契数列{1, 1, 2, 3, 5, 8, 13, 21, 34, 55 }发现斐波那契数列的两个相邻数 的比例,无限接近 黄金分割值0.618
斐波那契查找算法原理
斐波那契查找原理与前两种相似,仅仅改变了中间结点mid的位置,mid 不再是中间或插值得到,而是位
于黄金分割点附近,即 mid=low+F(k-1)-1(F 代表斐波那契数列),如下图所示
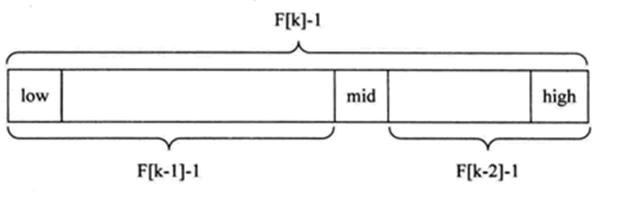
对 F(k-1)-1 的理解:
-
由斐波那契数列
F[k]=F[k-1]+F[k-2]的性质,可以得到(F[k]-1)=(F[k-1]-1)+(F[k-2]-1)+1。该式说明:
只要顺序表的长度为F[k]-1,则可以将该表分成长度为F[k-1]-1 和 F[k-2]-1的两段,即如上图所示。从而中间位置为
mid=low+F(k-1)-1 -
类似的,每一子段也可以用相同的方式分割
-
但顺序表长度
n不一定刚好等于F[k]-1,所以需要将原来的顺序表长度n增加至F[k]-1。这里的 k 值只要能使
得F[k]-1恰好大于或等于n即可,由以下代码得到,顺序表长度增加后,新增的位置(从n+1到F[k]-1位置),
都赋为n位置的值即可while(n>fib(k)-1) k++;
5.2、斐波那契查找代码实现
public class FibonacciSearch {
public static int maxSize = 20;
public static void main(String[] args) {
int [] arr = {1,8, 10, 89, 1000, 1234};
System.out.println("index=" + fibSearch(arr, 1234));
}
//因为后面我们mid=low+F(k-1)-1,需要使用到斐波那契数列,因此我们需要先获取到一个斐波那契数列
//非递归方法得到一个斐波那契数列
public static int[] fib() {
int[] f = new int[maxSize];
f[0] = 1;
f[1] = 1;
for (int i = 2; i < maxSize; i++) {
f[i] = f[i - 1] + f[i - 2];
}
return f;
}
//编写斐波那契查找算法
//使用非递归的方式编写算法
/**
*
* @param a 数组
* @param key 我们需要查找的关键码(值)
* @return 返回对应的下标,如果没有-1
*/
public static int fibSearch(int[] a, int key) {
int low = 0;
int high = a.length - 1;
int k = 0; //表示斐波那契分割数值的下标
int mid = 0; //存放mid值
int f[] = fib(); //获取到斐波那契数列
//获取到斐波那契分割数值的下标
while(high > f[k] - 1) {
k++;
}
//因为 f[k] 值 可能大于 a 的 长度,因此我们需要使用Arrays类,构造一个新的数组,并指向temp[]
//不足的部分会使用0填充
int[] temp = Arrays.copyOf(a, f[k]);
//实际上需求使用a数组最后的数填充 temp
//举例:
//temp = {1,8, 10, 89, 1000, 1234, 0, 0} => {1,8, 10, 89, 1000, 1234, 1234, 1234,}
for(int i = high + 1; i < temp.length; i++) {
temp[i] = a[high];
}
// 使用while来循环处理,找到我们的数 key
while (low <= high) { // 只要这个条件满足,就可以找
mid = low + f[k - 1] - 1;
if(key < temp[mid]) { //我们应该继续向数组的前面查找(左边)
high = mid - 1;
//为什么是 k--
//说明
//1. 全部元素 = 前面的元素 + 后边元素
//2. f[k] = f[k-1] + f[k-2]
//因为 前面有 f[k-1]个元素,所以可以继续拆分 f[k-1] = f[k-2] + f[k-3]
//即 在 f[k-1] 的前面继续查找 k--
//即下次循环 mid = f[k-1-1]-1
k--;
} else if ( key > temp[mid]) { // 我们应该继续向数组的后面查找(右边)
low = mid + 1;
//为什么是k -=2
//说明
//1. 全部元素 = 前面的元素 + 后边元素
//2. f[k] = f[k-1] + f[k-2]
//3. 因为后面我们有f[k-2] 所以可以继续拆分 f[k-2] = f[k-3] + f[k-4]
//4. 即在f[k-2] 的前面进行查找 k -=2
//5. 即下次循环 mid = f[k - 1 - 2] - 1
k -= 2;
} else { //找到
//需要确定,返回的是哪个下标
if(mid <= high) {
return mid;
} else {
return high;
}
}
}
return -1;
}
}
结果:

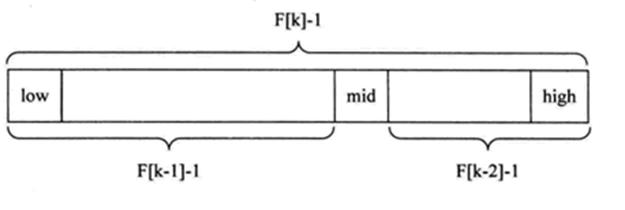
关于判断语句中的k--和 k -= 2,对着这张图,分析一下。
第一个if判断是向数组左边开始查找,那么对于左边的数据,相比全部数据而言,它的长度是f[k-1]-1,之后f[k-1]-1又作为一个整体来查找,即k要自减1。
对于右侧的数据,它的长度为f[k-2]-1,之后,它也会作为一个整体来查找,所以k要减2
5.3、斐波那契查找分析
复杂度分析:最坏情况下,时间复杂度为O(log2n),且其期望复杂度也为O(log2n)
6、分块查找
6.1、分块查找简介
分块查找,也叫索引顺序查找,算法实现除了需要查找表本身之外,还需要根据查找表建立一个索引表。例如
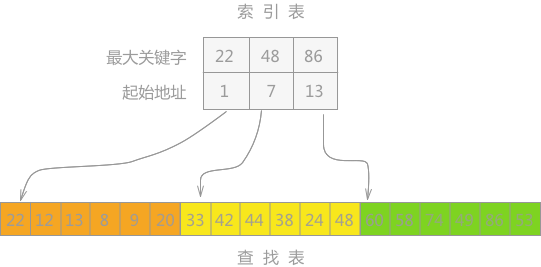
上图中,待查找表中共 18 个查找关键字,将其平均分为 3 个子表,对每个子表建立一个索引,索引中包含中两部分内容:
该子表部分中最大的关键字以及第一个关键字在总表中的位置,即该子表的起始位置。
建立的索引表要求按照关键字进行升序排序,查找表要么整体有序,要么分块有序
分块有序指的是子表中所有关键字都要大于前一个子表中的最大关键字,小于后一个子表中的最小关键字
块(子表)中各关键字的具体顺序,根据各自可能会被查找到的概率而定。如果各关键字被查找到的概率是相等的,那么可以随机存放;否则可按照被查找概率进行降序排序,以提高算法运行效率。
分块查找算法的运行效率受两部分影响:查找块的操作和块内查找的操作。
- 查找块的操作可以采用顺序查找,也可以采用折半查找(更优)
- 块内查找的操作采用顺序查找的方式。
总体来说,分块查找算法的效率是顺序查找和折半查找的结合体
6.2、分块查找代码实现
分块查找的过程分为两步进行:
- 确定要查找的关键字可能存在的具体块(子表)(对索引表中的最大关键字进行查找)
- 在具体的块中进行顺序查找
注:在第一步确定块(子表)时,由于索引表中按照关键字有序,所有可以采用二分查找算法。而在第二步中,由于各子表中关键字没有严格要求有序,所以只能采用顺序查找的方式。
代码
public class DayNineSearch {
public static void main(String[] args) {
Scanner input=new Scanner(System.in);
//原表
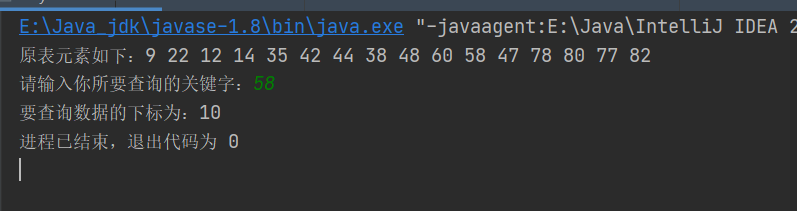
int a[]={9,22,12,14,35,42,44,38,48,60,58,47,78,80,77,82};
//分块获得对应的索引表,这里是一个以索引结点为元素的对象数组
BlockTable [] arr={
new BlockTable(22,0,3),//最大关键字为22 起始下标为0,3的块
new BlockTable(44,4,7),
new BlockTable(60,8,11),
new BlockTable(82,12,15)
};
//打印原表
System.out.print("原表元素如下:");
for (int i = 0; i < a.length; i++) {
System.out.print(a[i]+" ");
}
System.out.println();
//待查关键字
System.out.print("请输入你所要查询的关键字:");
int key=input.nextInt();
//调用分块查找算法,并输出查找的结果
int result=BlockSearch(a,arr,key);
System.out.print("要查询数据的下标为:"+result);
}
private static int BlockSearch(int a[],BlockTable[] arr,int key){
int left=0,right=arr.length-1;
//利用折半查找法查找元素所在的块
while(left<=right){
int mid=(right-left)/2+left;
if(arr[mid].key>=key){
right=mid-1;
}else{
left=mid+1;
}
}
//循环结束,元素所在的块为right+1 取对应左区间下标作为循环的开始点
int i=arr[right+1].low;
//在块内进行顺序查找确定记录的最终位置
while(i<=arr[right+1].high&&a[i]!=key){
i++;
}
//如果下标在块的范围之内,说明查找成功,否则失败
if(i<=arr[right+1].high){
return i;
}else{
return -1;
}
}
}
//索引表结点
class BlockTable{
int key;
int low;
int high;
BlockTable(int key,int low,int high){
this.key=key;
this.low=low;
this.high=high;
}
}
结果:
6.3、分块查找分析
优点:
- 在表中插入和删除元素时,只需要找到对应的块,就可以在块内进行插入和删除运算
- 块内无序,插入和删除都较为容易,无需进行大量移动
- 适合线性表既要快速查找又要经常动态变化的场景
缺点:
- 需要增加一个存储索引表的内存空间
- 需要对初始索引表按照其最大关键字(或最小关键字)进行排序运算
时间复杂度:不超过O(n)
7、哈希查找
哈希查找即使用哈希表来实现查找功能,接下来我们就来看一下如何实现哈希表
7.1、实际需求
在学习哈希表之前,我们先看一个实际的需求:
有一个公司,当有新的员工来报道时,要求将该员工的信息加入(id,姓名),当输入该员工的id时,要求查找到该员工的 所有信息.
要求: 不使用数据库,尽量节省内存,速度越快越好
如何实现这个实际的需求呢?
这里就需要用到哈希表(散列)了,接下来让我们来详细了解一下什么是哈希表并且如何实现这个实际的需求。
7.2、哈希表简介
散列表(Hash table,也叫哈希表),是根据关键码值(Key value)而直接进行访问的数据结构。也就是说,它通
过把关键码值映射到表中一个位置来访问记录,以加快查找的速度。这个映射函数叫做散列函数,存放记录的数组
叫做散列表。
注:
1、一个数据转化为数组长度范围内的下标值的过程就称作为 哈希化,而实现哈希化的代码一般会封装在一个函数里,这个函数就叫做 哈希函数
2、上图使用拉链法解决冲突问题
7.3、冲突及解决
冲突,其含义就是在哈希化以后有几个元素的下标值相同,这就叫做 冲突。 那当两个元素的下标值冲突时,是后一个元素是不是要替换掉前一个元素呢?当然不是!
那么如何解决冲突这个现象呢?一般是有两种方法,即拉链法(链地址法) 和 开放地址法
注:哈希表冲突及解决部分参考于以下博客:
【数据结构与算法】详解什么是哈希表,并用代码手动实现一个哈希表
7.3.1、拉链法(常用)
这种方法是很常用的解决冲突的方法。我们举个例子来说,10本图书通过哈希化以后存入到长度为10的数组当中,难免有几本书的下标值是相同的,那么我们可以将这两个下标值相同的元素存入到一个单独的数组中,然后将该数组存放在他们原本所在数组的下标位置,如图
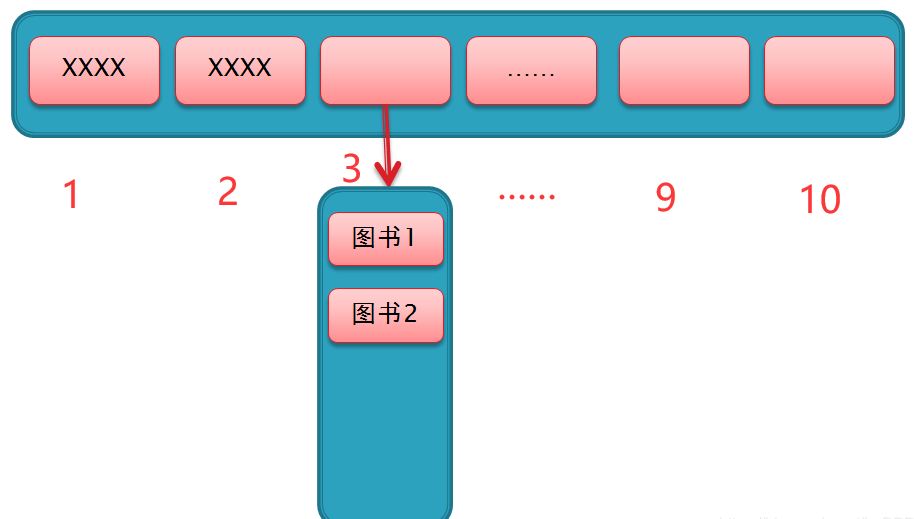
假设图书1 和 图书2 哈希化后的下标值都为3,那么我们就可以在原数组下标3的位置放一个数组,同时存放这两本图书。因此,无论是查询哪本图书,计算机获得的下标值都是3,然后再对这个位置的数组进行遍历即可获得想要的图书。
这是第一种解决 冲突 的方法,但使用是还是需要考虑数组长度是否合适的。
7.3.2、开放地址法
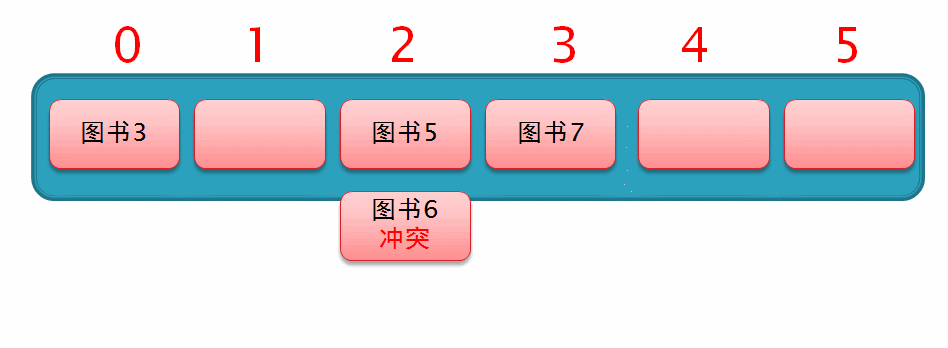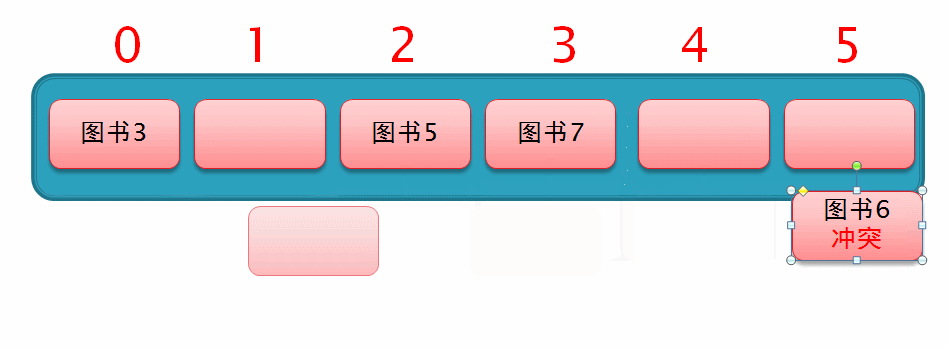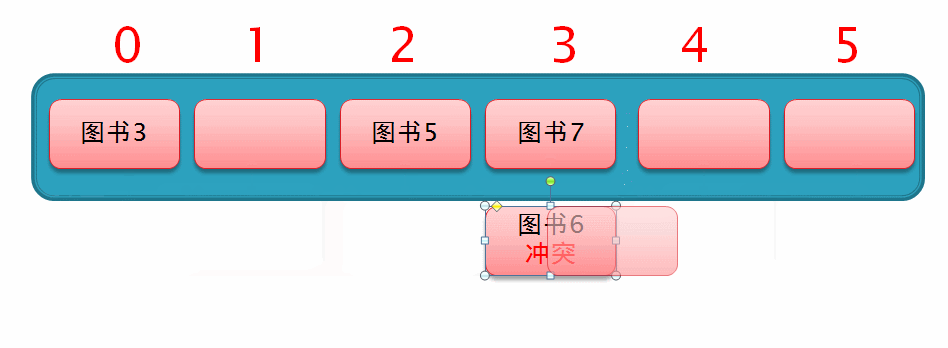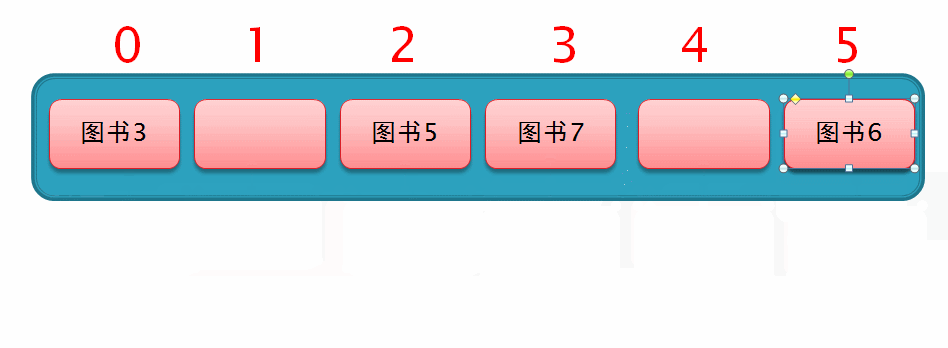
这种方法简单来说就是当元素下标值发生冲突时,寻找空白的位置插入数据。假设当前下标值为1和3的位置分别已经插入了 图书3 和 图书5,这时将 图书6 进行哈希化,发现它的下标值也是1,此时与 图书3 发生冲突,那么此时 图书6 就可以找到下一个空着的没插入元素的位置进行插入,如图
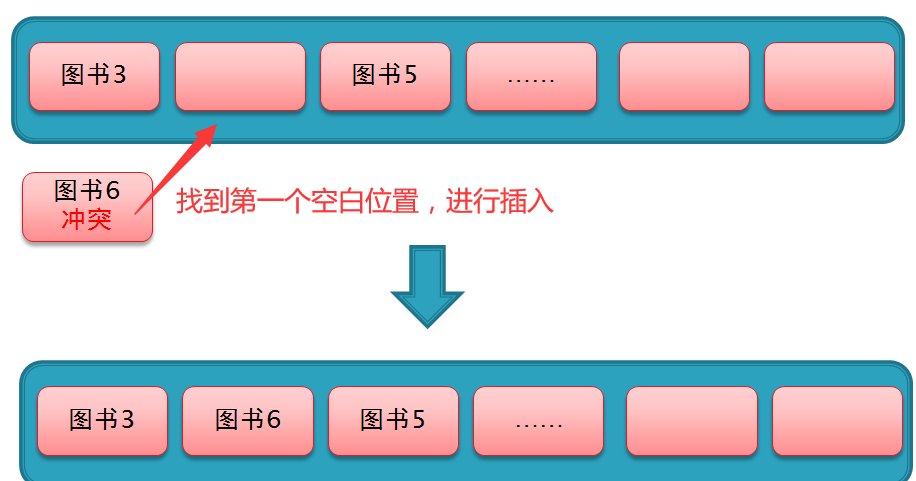
其实当发生冲突时,寻找空白的位置也有三种方法,分别是 线性探测 、二次探测 、再哈希法
1、线性探测
顾名思义,线性探测的意思就是,当某两个元素发生冲突时,将当前索引+1,查看该位置是否为空,是的话就插入数据,否则就继续将索引+1,以此类推……直到插入数据位置。
但这种方法有一个缺点,那就是当数组中连续很长的一个片段都已经插入了数据,此时用线性探测就显得效率没那么高了,因为每次探测的步长都为1,所以这段都已经插入了数据的片段都得进行探测一次,这种现象叫做 聚集。如下图,就是一个典型的聚集现象

图书8 的下标值为1,与 图书3 冲突,然后进行线性探测,依次经过 图书6、5、1、7 都没有发现有空白位置可以插入,直到末尾才找到空白位置插入,这样挺不好的,所以我们可以选用 二次探测 来缓解 聚集 这种现象。
2、二次探测
二次探测 在线性探测的基础上,将每次探测的步长改为了当前下标值 index + 1² 、index + 2² 、 index + 3² …… 直到找到空白位置插入元素为止
还是举一个例子来理解一下 二次探测 吧
假如现在已存入 图书3 、图书5 、图书7,如图

然后此时要存入一个 图书6,通过哈希化以后求得的下标值为2,与 图书5 冲突了,所以就从索引2的位置向后再移动 1² 个位置,但此时该位置上已存有数据,如下面这个动图演示
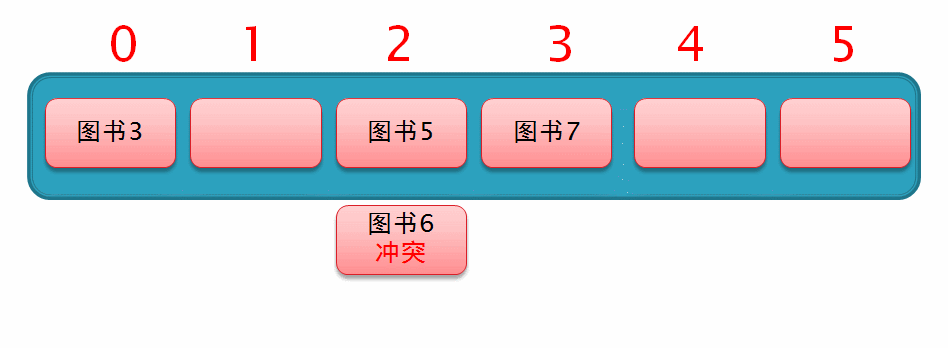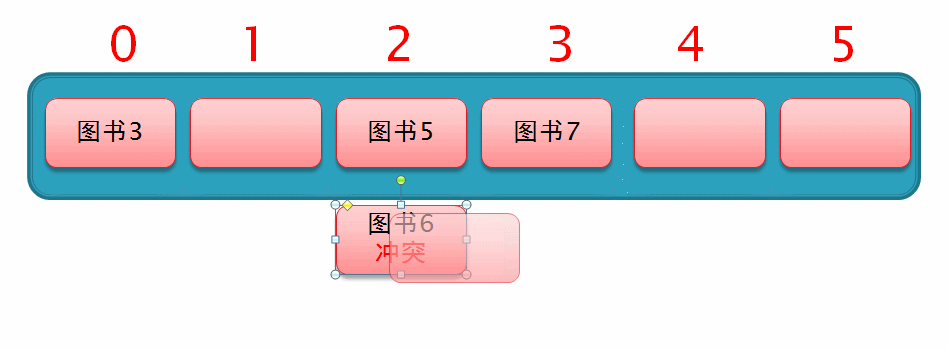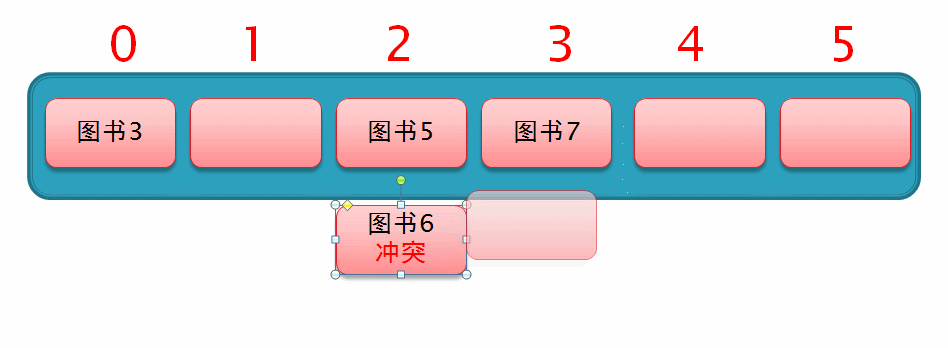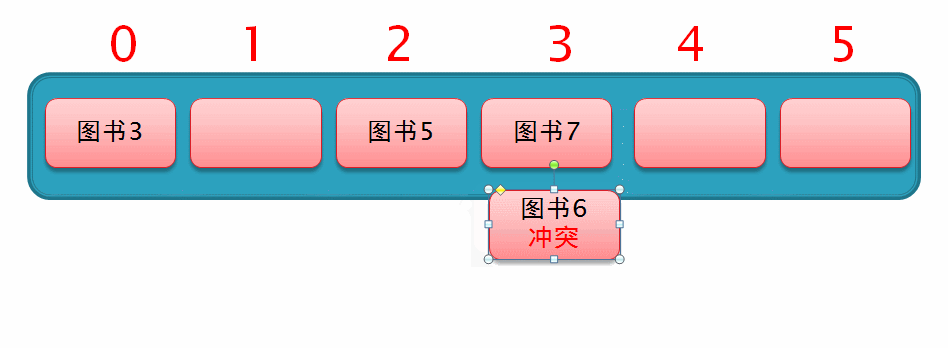
所以此时从索引为2的位置向后移动 2² 个位置,此时发现移动后的位置上也已存有数据,所以仍无法插入数据,如下面这个动图演示
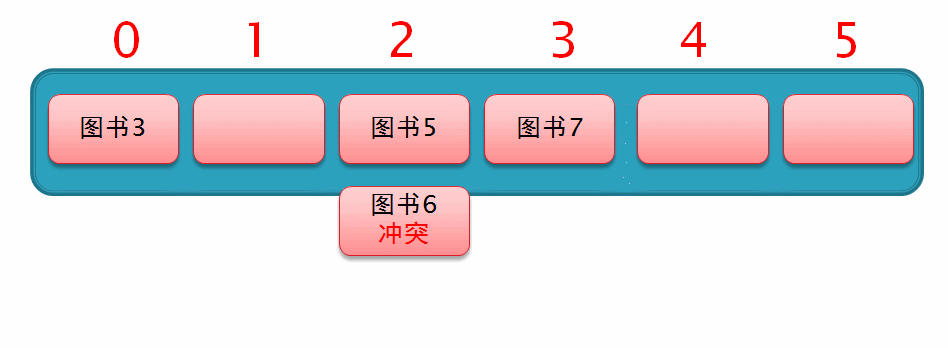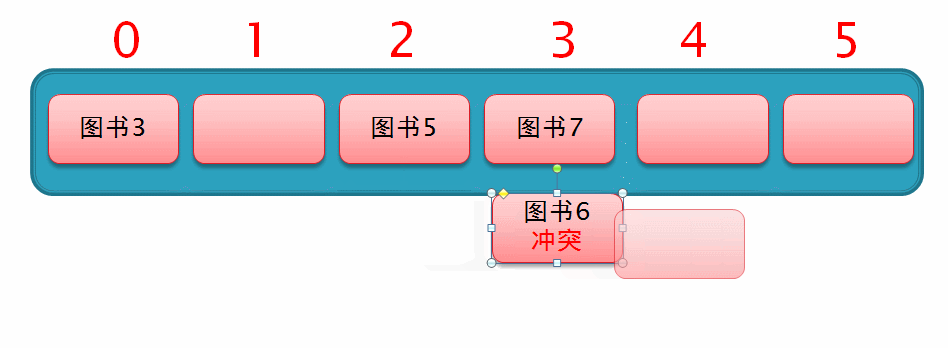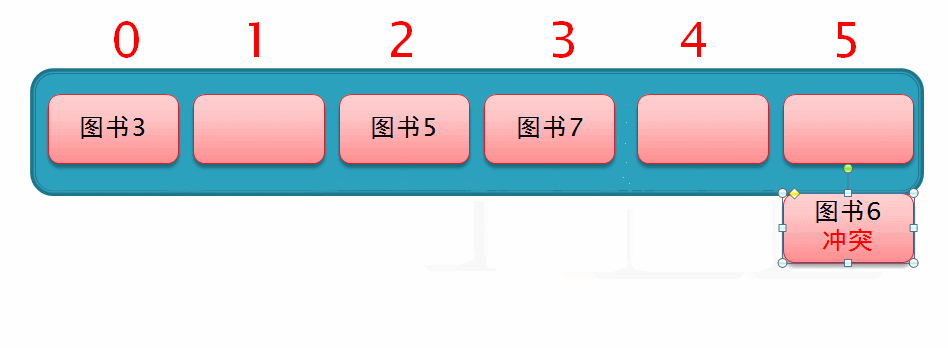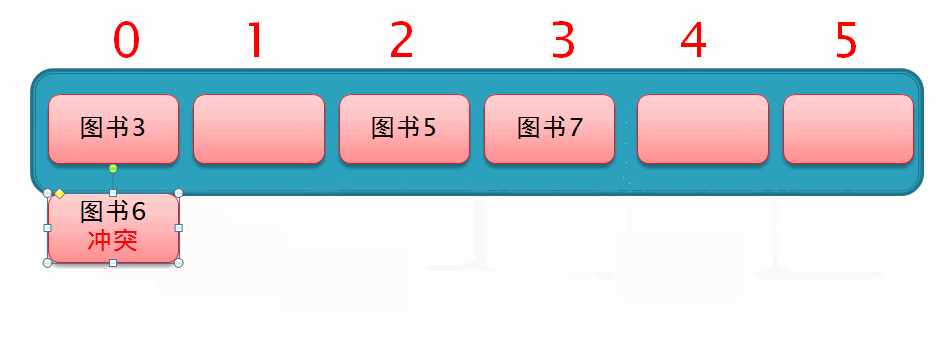
因此,我们继续从索引2的位置向后移动 3² 个位置,此时发现,移动后的位置上有空余位置,于是直接在此插入数据,这样一个二次探测的过程就完成了,如下列动图演示
我们可以看到,二次探测 在一定程度上解决了 线性探测 造成的 聚集 问题,但是它却在另一种程度造成了一种聚集,就比如 1² 、2² 、3² …… n² 上的聚集。所以这种方式还是有点不太好。
3、再哈希法
再哈希法 就是再将我们传入的值进行一次 哈希化,获得一个新的探测步数 step,然后按照这个步数进行探测,找到第一个空着的位置插入数据。这在很大的程度上解决了 聚集 的问题。
既然要再进行哈希化获得一个探测的步数,那么这个哈希化的处理过程一定要跟第一次哈希化的处理过程不一样,这样才能确认一个合适的搜索步长,提高查找效率。
这里,我们就不用担心如何写一个不一样的哈希函数了,给大家看一个公认的比较好的哈希函数:step = constant - (key % constant)
其中,constant 是一个自己定的质数常量,且小于数组的容量; key 就是第一次哈希化得到得值。
然后我们再通过这个函数算得的步长来进行查找搜索空位置进行插入即可,这里就不做过多的演示了。
7.4、代码实现
现在我们回到最开始的需求:有一个公司,当有新的员工来报道时,要求将该员工的信息加入(id,名字),当输入该员工的 id 时,要求查找到该员工的 所有信息.
要求:
-
不使用数据库,,速度越快越好=>哈希表(散列)
-
添加时,保证按照 id 从低到高插入 [思考: 如果 id 不是从低到高插入,但要求各条链表仍是从低到
高,怎么解决?] -
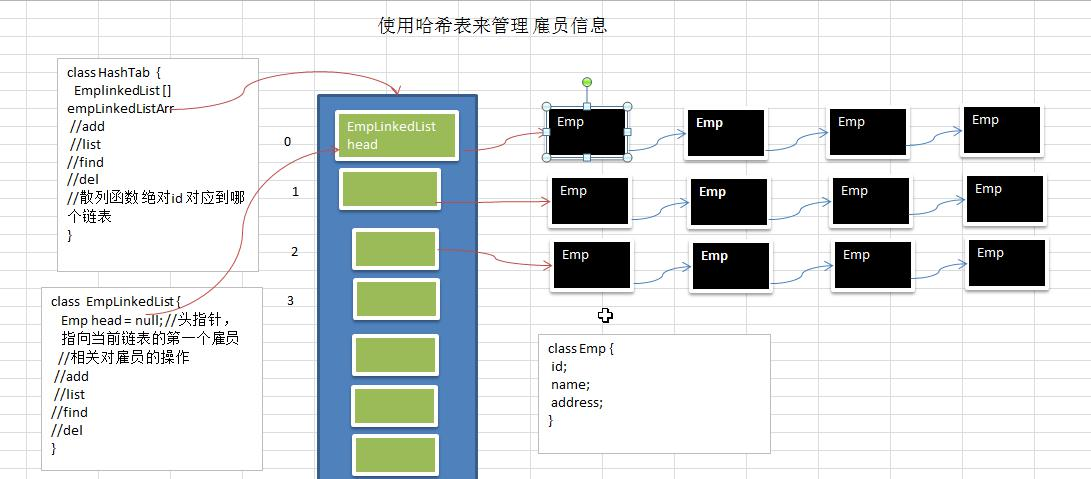
使用链表来实现哈希表, 该链表不带表头[即: 链表的第一个结点就存放雇员信息]
-
思路分析并画出示意图
代码实现
public class HashTabDemo {
public static void main(String[] args) {
//创建哈希表
HashTab hashTab = new HashTab(7);
//写一个简单的菜单
String key = "";
Scanner scanner = new Scanner(System.in);
while(true) {
System.out.println("add: 添加雇员");
System.out.println("list: 显示雇员");
System.out.println("find: 查找雇员");
System.out.println("exit: 退出系统");
key = scanner.next();
switch (key) {
case "add":
System.out.println("输入id");
int id = scanner.nextInt();
System.out.println("输入名字");
String name = scanner.next();
//创建 雇员
Emp emp = new Emp(id, name);
hashTab.add(emp);
break;
case "list":
hashTab.list();
break;
case "find":
System.out.println("请输入要查找的id");
id = scanner.nextInt();
hashTab.findEmpById(id);
break;
case "exit":
scanner.close();
System.exit(0);
default:
break;
}
}
}
}
//创建HashTab 管理多条链表
class HashTab {
private EmpLinkedList[] empLinkedListArray;
private int size; //表示有多少条链表
//构造器
public HashTab(int size) {
this.size = size;
//初始化empLinkedListArray
empLinkedListArray = new EmpLinkedList[size];
//?留一个坑, 这时不要分别初始化每个链表
for(int i = 0; i < size; i++) {
empLinkedListArray[i] = new EmpLinkedList();
}
}
//添加雇员
public void add(Emp emp) {
//根据员工的id ,得到该员工应当添加到哪条链表
int empLinkedListNO = hashFun(emp.id);
//将emp 添加到对应的链表中
empLinkedListArray[empLinkedListNO].add(emp);
}
//遍历所有的链表,遍历hashtab
public void list() {
for(int i = 0; i < size; i++) {
empLinkedListArray[i].list(i);
}
}
//根据输入的id,查找雇员
public void findEmpById(int id) {
//使用散列函数确定到哪条链表查找
int empLinkedListNO = hashFun(id);
Emp emp = empLinkedListArray[empLinkedListNO].findEmpById(id);
if(emp != null) {//找到
System.out.printf("在第%d条链表中找到 雇员 id = %d\n", (empLinkedListNO + 1), id);
}else{
System.out.println("在哈希表中,没有找到该雇员~");
}
}
//编写散列函数, 使用一个简单取模法
public int hashFun(int id) {
return id % size;
}
}
//表示一个雇员
class Emp {
public int id;
public String name;
public Emp next; //next 默认为 null
public Emp(int id, String name) {
super();
this.id = id;
this.name = name;
}
}
//创建EmpLinkedList ,表示链表
class EmpLinkedList {
//头指针,执行第一个Emp,因此我们这个链表的head 是直接指向第一个Emp
private Emp head; //默认null
//添加雇员到链表
//说明
//1. 假定,当添加雇员时,id 是自增长,即id的分配总是从小到大
// 因此我们将该雇员直接加入到本链表的最后即可
public void add(Emp emp) {
//如果是添加第一个雇员
if(head == null) {
head = emp;
return;
}
//如果不是第一个雇员,则使用一个辅助的指针,帮助定位到最后
Emp curEmp = head;
while(true) {
if(curEmp.next == null) {//说明到链表最后
break;
}
curEmp = curEmp.next; //后移
}
//退出时直接将emp 加入链表
curEmp.next = emp;
}
//遍历链表的雇员信息
public void list(int no) {
if(head == null) { //说明链表为空
System.out.println("第 "+(no+1)+" 链表为空");
return;
}
System.out.print("第 "+(no+1)+" 链表的信息为");
Emp curEmp = head; //辅助指针
while(true) {
System.out.printf(" => id=%d name=%s\t", curEmp.id, curEmp.name);
if(curEmp.next == null) {//说明curEmp已经是最后结点
break;
}
curEmp = curEmp.next; //后移,遍历
}
System.out.println();
}
//根据id查找雇员
//如果查找到,就返回Emp, 如果没有找到,就返回null
public Emp findEmpById(int id) {
//判断链表是否为空
if(head == null) {
System.out.println("链表为空");
return null;
}
//辅助指针
Emp curEmp = head;
while(true) {
if(curEmp.id == id) {//找到
break;//这时curEmp就指向要查找的雇员
}
//退出
if(curEmp.next == null) {//说明遍历当前链表没有找到该雇员
curEmp = null;
break;
}
curEmp = curEmp.next;//以后
}
return curEmp;
}
}
结果:
(1)添加员工

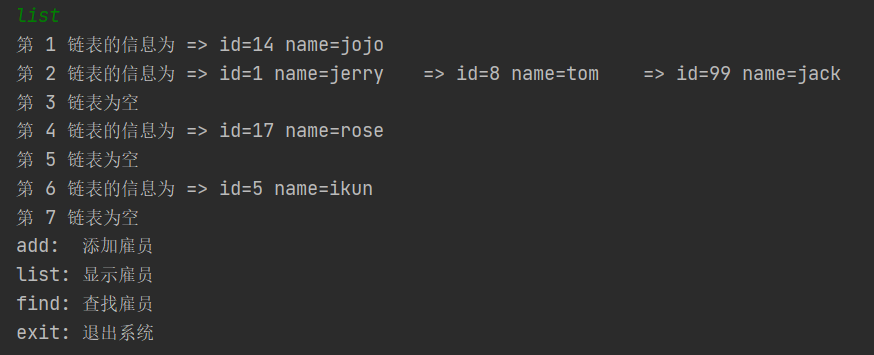
(2)显示所有员工
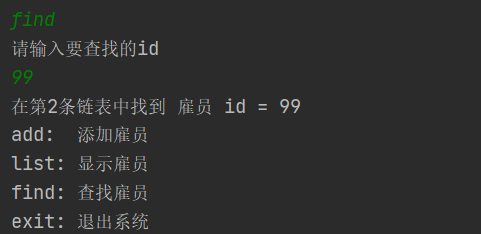
(3)查找指定id的员工
7.5、哈希表分析
1、优点
首先是哈希表的优点:
- 无论数据有多少,处理起来都特别的快
- 能够快速地进行
插入修改元素、删除元素、查找元素等操作 - 代码简单(其实只需要把哈希函数写好,之后的代码就很简单了)
2、缺点
然后再来讲讲哈希表的缺点:
- 哈希表中的数据是没有顺序的
- 数据不允许重复
3、时间复杂度:O(1)
8、树表查找
树表查找大致分为以下三种,具体的查找分析会在关于树的数据结构与算法中详细介绍,我们先来看一看它们的时间复杂度:
- 二叉查找树:O(log2n)~O(n)之间
- 红黑树:O(logn)
- B和B+树:O(log2n)
9、七大查找算法总结
9.1、分类
9.2时间复杂度大对比:
| 平均时间复杂度 | 最差查找时间 | 前提 | |
|---|---|---|---|
| 顺序查找 | O(n) | O(n) | 无 |
| 二分查找 | O(log2n) | O(log2n) | 有序 |
| 插值查找 | O(log(2)(log(2)n)) | O(log(2)(log(2)n)) | 有序 |
| 斐波那契查找 | O(log2n) | O(log2n) | 有序+斐波那契数列 |
| 分块查找 | O(log2n)~O(n) | O(n) | 创建区块 |
| 哈希查找 | O(1) | O(k) | 创建哈希表 |
1、顺序查找:
(1)最好情况:要查找的第一个就是。时间复杂度为:O(1)
(2)最坏情况:最后一个是要查找的元素。时间复杂度为:O(n)
(3)平均情况下就是:(n+1)/2。
所以总的来说时间复杂度为:O(n)
2、二分查找:O(log2n)--->log以2为底n的对数
解释:2^t = n; t = log(2)n;
3、插值查找:O(log(2)(log(2)n))--->log以2为底的(log以2为底的n的对数)的对数
4、斐波那契查找:O(log2n)--->log以2为底n的对数
5、分块查找:O(log2n)~O(n)之间
6、哈希查找:O(1)
7、树表查找:
(1)二叉查找树:O(log2n)~O(n)之间
(2)红黑树:O(lgn)(以10为底n的对数)
(3)B和B+树:O(log2n)
结论:
-
从结果中可以看出散列表(哈希表)的速度是最快的,其次是红黑树,二分查找树和二分查找差不多,顺序查找速度特别慢.所以在不考虑有序性相关的操作之外,散列表无疑是最优选择,而且实现简单.其次才考虑红黑树,虽然性能很好,但实现复杂.
-
相对二叉查找树,散列表的优点在于代码更简单,且查找时间最优(常数级别,只要键的数据类型是标准的或者简单到我们可以为它写出满足均匀性假设的高效散列函数即可).
-
二叉查找树相对于散列表的优点在于抽象结构更简单(不需要设计散列函数),红黑树可以保证最坏情况下的性能且它能够支持的操作更多(如排名、选择、排序和范围查找).根据经验法则,大多数程序员的第一选择是散列表,在其他因素更重要时才会选择红黑树.
到这里关于查找算法的内容就结束了,其中基于树结构的查找知识只是做了简单的介绍,详细的内容我会在树的数据结构与算法部分作具体说明,希望这篇文章对大家有所帮助(•ㅂ•)/♥


