序列变换

题意

把 \(2n\) 长字符串的字符串变成形如 ((...)) 的字符串。

• 操作 1：p(A)(B)q \(\to\) p(A()B)q 花费 \(x \times v_1 + y\times v_2\)，\(v1, v2\) 分别是两个左括号的权值。

• 操作 2: pABq \(\to\) pBAq, 无花费。

求最小花费。

括号树

将括号序列变成括号树。

为了方便，强制将原串 \(s\) 变成 \((s)\)，其中左括号的花费为 \(0\)。

• 令 \(S(u)\) 表示节点 \(u\) 及其子树所代表的括号序列。

  定义括号树中父亲和儿子的关系：

  \[S(u) = ( + S(v_1) + S(v_2) + ... + S(v_m) + ) \]

  其中 \(v_{1..m}\) 是 \(u\) 的儿子。

• 令 \(\text{val}(u)\) 表示这个节点代表的左括号的权值。

  每个节点的括号序列是儿子的括号序列连接，并放进一个括号里。

  该点的权值就是放入的括号中的左括号的权值。

具体化两个操作。

1. 记代表 \((A)\) 的节点是 \(a\), 代表 \((B)\) 的节点是 \(b\)。

   这个操作相当于：
   把 \(b\) 所有儿子变成 \(a\) 的儿子，这时 \(b\) 只代表一个括号，再将 \(b\) 变成 \(a\) 的儿子。

   随手画个图:
   

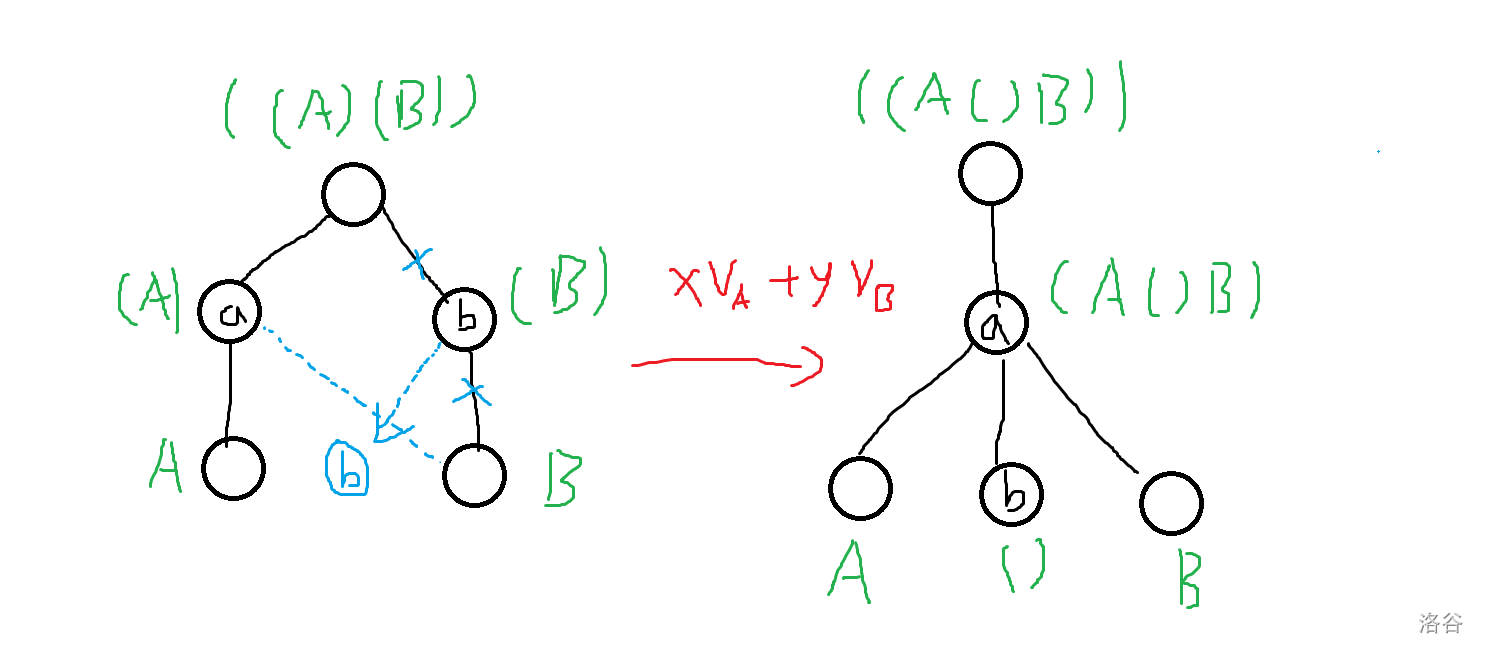
2. 实际上就是任意交换子树。

   

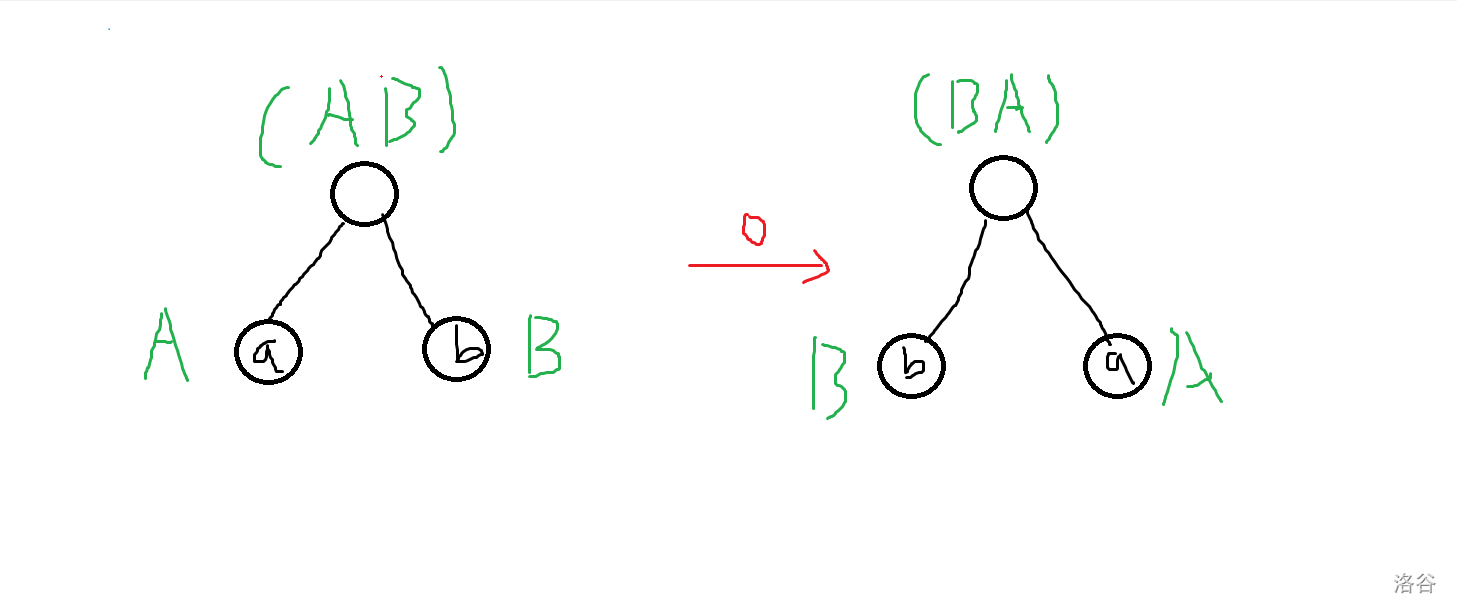
3. 目标：就是一条长 \(n + 1\) 的链，\(+ 1\) 是强制加入的一对括号。

这些操作也是有些性质的。

1. 最终的括号树，有 \(n + 1\) 层，每层只有 \(1\) 个点。

2. 操作只能将一个点往下移，也可以将任意两个点凑成一对。

分类讨论

考虑对 \(x, y\) 的情况分类讨论。

1. \(x = 0, y = 0\) 时。

   显然结果是 \(0\)。

2. \(x = 0, y = 1\) 时。

   这时的花费来源是每次操作中节点 \(b\) 的左括号。

   一个明显的策略是每层留下最大值，剩下的点往下层移。

   假如被留下的不是最大值，现在得到了最小花费，将这个值替换后面的最大值并产生花费，这样一定比最小花费还要优。

3. \(x = 1, y = 1\) 时。

   这时的花费来源是每次操作中节点 \(a\) 和节点 \(b\) 的左括号。

   这时的策略也是每一层留下最大值，并且每次将最小值作为节点 \(a\)。

   设 \(\text{sz}\) 是当前节点的个数，\(\text{sum}\) 是所有的数的和，这层的贡献就是 \(\min \times (\text{sz} - 2) + \text{sum}\)。

   其实也差不多是上面的办法来说明，如果不是留下最大值，将它代替最大值后，在这一层和在后面层的贡献都更优。

4. \(x = 1, y = 0\) 时。

   首先每一层留下来的数都一定会被算入贡献，除了原本就只有一个数的前几层和最后一层，这样的贡献是固定的。

   在每一层把点往下移时，也是考虑将最小值当成节点 \(a\)，这样的贡献与当前层最小值有关。

   最后一层的值不会贡献，要使总花费最小，这样的贡献与最后的最大值有关。

   分类讨论一下每层 \(\text{sz}\) 的贡献情况。

   1. \(\text{sz} = 1\)

      没有贡献。

   2. \(\text{sz} > 2\)

      这时最小值和最大值都能下放，那就都下放，一定不会更劣。留下的值总和是固定的。

      下放操作产生的贡献是 \((\text{sz} - 2) \times \min\)。

   3. \(\text{sz} = 2\)

      这时只能下放当前层的最小值或最大值。

      思考一下括号树的样子。

      原先的样子: \(1,...,1,2,1,...,1,\geq 2, ...\)。

      下放后每一层的样子: \(1,...,1,2,2,...,2,\geq 3, ..., 2, 1\)。

      也就是所如果知道连续一段 \(2\) 后下放了的数，就能确定最后的贡献。

      这时有个性质：下放的是一段连续 \(2\) 中的最大值或最小值是最优的。

      可以想到，这些 \(\text{sz} = 2\) 的贡献只有留下来的值，并且这些值在不同方案里的值只与下放的是是不是最后一层的值有关，那么下放最大值肯定优。

      然鹅还有最小值在中间当 \(a\) 节点，下放最小值也是在这种情况最优。
      于是分两种情况分别计算即可。

代码

#include<bits/stdc++.h>
using namespace std;

using ll = long long; 
const int MAXN = 4000010; 
const int INF = 0x3f3f3f3f;
int n, x, y; 
char a[MAXN]; 
int val[MAXN]; 

void solve1() {
	vector<vector<int>> v(n / 2 + 2); 
	vector<stack<int>> st(n / 2 + 2); 
	int s = 0;
	for (int i = 0; i <= n + 1; i ++) {
		if (a[i] == '(') {
			s ++; 
			st[s].push(i); 
		}
		if (a[i] == ')') {
			int dep = s, l = st[s].top(); 
			st[s].pop();   
			v[dep].emplace_back(val[l]); 
			s --;
		}
		assert(s >= 0); 
	} 
	
	ll ans = 0; 
	priority_queue<int> q; 
	ll sum = 0; 
	for(int i = 1; i <= n / 2 + 1; i ++) {
		for (auto j : v[i]) 
			q.push(j), 
			sum += j;
			
		sum -= q.top();  
		q.pop(); 
		ans += sum; 
	}
	cout << ans; 
}
void solve2() {
	vector<vector<int>> v(n / 2 + 2); 
	vector<stack<int>> st(n / 2 + 2); 
	int s = 0;
	for (int i = 0; i <= n + 1; i ++) {
		if (a[i] == '(') {
			s ++; 
			st[s].push(i); 
		}
		if (a[i] == ')') {
			int dep = s, l = st[s].top(); 
			st[s].pop();   
			v[dep].emplace_back(val[l]); 
			s --;
		}
		assert(s >= 0); 
	} 
	
	ll ans = 0; 
	multiset<int> q; 
	ll sum = 0; 
	for(int i = 1; i <= n / 2 + 1; i ++) {
		for (auto j : v[i]) 
			q.insert(j), 
			sum += j;
		if (int(q.size()) > 1)
			ans += sum + *q.begin() * (q.size() - 2); 
		sum -= *prev(q.end()); 
		q.erase(prev(q.end()));   
	}
	cout << ans; 
}
void solve3() {
	vector<vector<int>> v(n / 2 + 2); 
	vector<stack<int>> st(n / 2 + 2); 
	int s = 0;
	for (int i = 0; i <= n + 1; i ++) {
		if (a[i] == '(') {
			s ++; 
			st[s].push(i); 
		}
		if (a[i] == ')') {
			int dep = s, l = st[s].top(); 
			st[s].pop();   
			v[dep].emplace_back(val[l]); 
			s --;
		}
		assert(s >= 0); 
	} 
	
	int p = 1, q = 0, m = n / 2 + 1; 
 
	while (v[p].size() == 1 && p <= m) p ++;
	q = p + 1;
	while (v[q].size() == 1 && q <= m) q ++;
	ll dec = 0;
	for (int i = 1; i < p; i ++)
		dec += v[i][0]; 
	int ma1 = 0, mi1 = INF,
		ma2 = 0, mi2 = INF; 	
	ma1 = max({ma1, v[p][0], v[p][1]}), 
	mi2 = min({mi2, v[p][0], v[p][1]}); 
	for (int i = p + 1; i < q; i ++)	
		ma1 = max(ma1, v[i][0]), 
		mi2 = min(mi2, v[i][0]); 
	
	ll ans1 = 0, ans2 = 0; 
	ll siz = 1; 
	for (int i = q; i < m; i ++) {
		for (auto j : v[i])
			ma1 = max(ma1, j), 
			mi1 = min(mi1, j),
			ma2 = max(ma2, j), 
			mi2 = min(mi2, j);
		siz += int(v[i].size());  
		ans1 += mi1 * (siz - 2); 
		ans2 += mi2 * (siz - 2); 
		siz --; 
	}
	cout << min(ans1 - ma1, ans2 - ma2) + accumulate(val + 1, val + n + 1, 0ll, [](ll sum, int x) {return sum + x;}) - dec; 
}

int main() { 
	ios::sync_with_stdio(false); 
	cin.tie(0); cout.tie(0);
	cin >> n >> x >> y; 
	n <<= 1; 
	for (int i = 1; i <= n; i ++)
		cin >> a[i];
	for (int i = 1; i <= n; i ++) 
		if (a[i] == '(')
			cin >> val[i]; 
	
	a[0] = '(', a[n + 1] = ')'; 
	if (x == 0 && y == 0) {
		cout << 0;  
		return 0; 
	}
	if (x == 0 && y == 1) {
		solve1(); 
	}
	if (x == 1 && y == 1) {
		solve2(); 
	}
	if (x == 1 && y == 0) {
		solve3(); 
	}
	return 0; 
}
/*
4 0 1
()()()()
1 2 3 4
*/