平衡二叉查找树--伸展树splay
splay树,又称伸展树,是一种平衡二叉查找树,通过不断把每个节点旋转到根节点能够在O(logN)的时间内完成插入、查找以及删除的操作,并且能保持平衡不会退化成链
一、关于二叉查找树
首先,二叉查找树肯定是个二叉树(废话),每个节点的左子节点的值小于该节点的值小于右子节点的值。如下
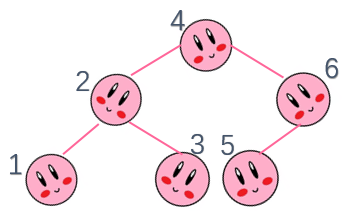
一般二叉查找树的每个节点会带两种变量,一种是优先级,一种是该节点所代表的信息,以该节点的优先级建堆就可以得到一个二叉查找树
很显然二叉查找树找到一个节点所花费的时间与其深度成正比,最好情况下花费为O(log n),最坏情况下为O(n),即,树退化成了一条链
当花费为O(log n)时,树是一种类似完全二叉树的形态,这个时候我们称这棵树是平衡的,即这棵树是一个平衡查找二叉树(是的,这个名字就是如此的简单粗暴)
二、平衡树
如果一棵树的每一个节点的左子树和右子树的高度差最多为一,则称这个树是平衡的,一个合理的二叉搜索树即一个平衡查找二叉树的插入和查找时间可以缩短到O(log n)(这是显然的,因为当这棵树是平衡的时其深度会最小)
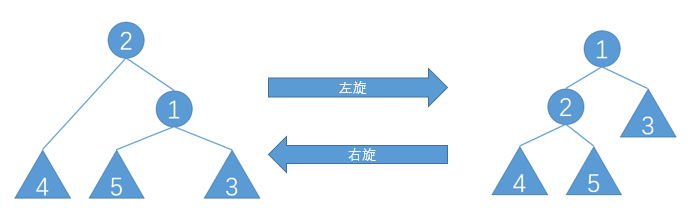
在插入和删除的过程中,二叉查找树可能会失衡,平衡树会通过“旋转”操作调整整棵二叉树的形态,其基本操作为左旋(zig)和右旋(zag),若要被旋转的点是其父节点的左子节点则进行右旋,反之左旋
为了使得这棵树的中序遍历不变,左旋内容如下:
一、使该节点的左子树成为该节点父节点的右子树
二、使该节点的父节点成为该节点的左子树
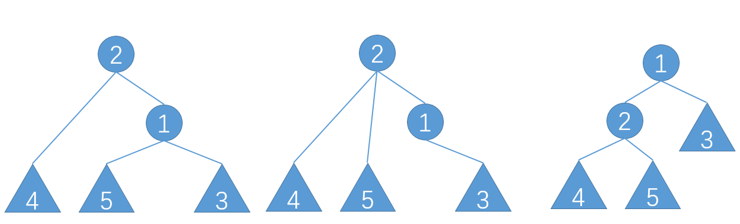
右旋同理
经过尝试,如果某个节点需要连续进行若干次(大于等于4次)的左旋或若干次右旋操作时,会有一种更优的旋转方法称为双旋
就比如下面这个例子,若我要把节点5旋转到根节点
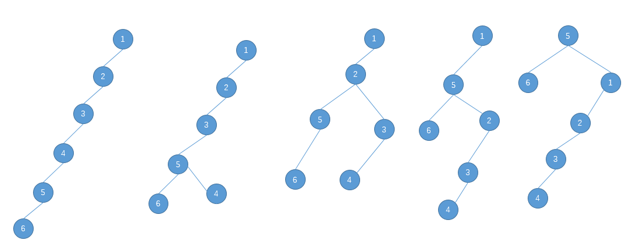
最终这棵树的深度是5
但如果每次旋转节点5之前我们先旋转其父节点,然后再旋转节点5,直到节点5成为根节点,最终会有不同的效果
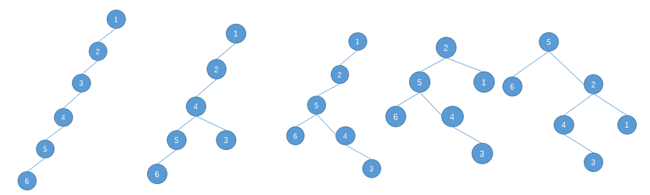
显然,第二种转法在转完后整棵树的深度比第一种转法整棵树的深度小一,根据前文提到的关于查找树的复杂度,第二种转法更优
这还只是五次右旋,如果连续旋转的次数更多,第二种转法与第一种的差距会越来越大,第二种转法就是所谓的双旋
看下代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | void rotate(int x){ int fa=f[x],grand=f[fa],son1=get(x),son2=(son1+1)%2;//f存储某节点的父节点编号 get是查找该节点是其父节点的左子节点还是右子节点 0为左 1为右 sons[fa][son1]=sons[x][son2];//将子节点挂到父节点上去 f[sons[fa][son1]]=fa; sons[x][son2]=fa; f[fa]=x;//更新关系 f[x]=grand; if(grand) { sons[grand][sons[grand][1]==fa]=x;//如果有祖父节点要令祖父节点成为该节点的父节点 } //upd(fa); //upd(x);}void splay(int x){ for(int fa;fa=f[x];rotate(x))//旋转直到x成为根节点 { if(f[fa]) rotate((get(x)==get(fa))?fa:x);//双旋 } root=x;//更新根节点 } |
在保持中序遍历不变的前提下,使用若干次“旋转”操作可以使这棵树平衡
三、伸展树splay的引入
splay实际上不算是严格的平衡树,事实上很多情况下它都不咋平衡,但是却能够在均摊O(logn)时间内完成插入,查找和删除操作,并且不至于退化为链
至于为什么能够均摊O(logn)的时间……这个算起来挺复杂的,这里就不赘述了因为我不会
splay的主要功能包括高效的插入、删除、查询、修改
先来看看插入如何实现
1、如果根节点为空,非常显然的事,这根本不需要插入,因为原本就没有树!直接让该节点成为根节点
代码如下
1 2 3 4 5 6 7 8 9 | if(!root)//如果根节点为空 { whole_size++;//整棵树的大小增加一 sons[whole_size][0]=sons[whole_size][1]=f[whole_size]=0;//默认有一定BST基础,所以这是一个很显然的初始化 root=whole_size;//初始化根节点 sub_size[whole_size]=cnt[whole_size]++;//sub_size 指的是以某节点为根节点的子树的大小 cnt存储的是某数被插入的次数 val[whole_size]=x;//该节点的数值 return ; } |
2、如果根节点不为空,根据二叉查找树的性质,从根节点起,若该数小于当前节点往左子树走,反之则往右子树,如果等于,则当前节点的cnt++
如果走到了一个为空的子树,则直接添加该节点
然后,将新添加的节点或刚累加了cnt的节点旋转至根节点
例如,现在在已有的树上插入一个3一个6
第一次

第二次
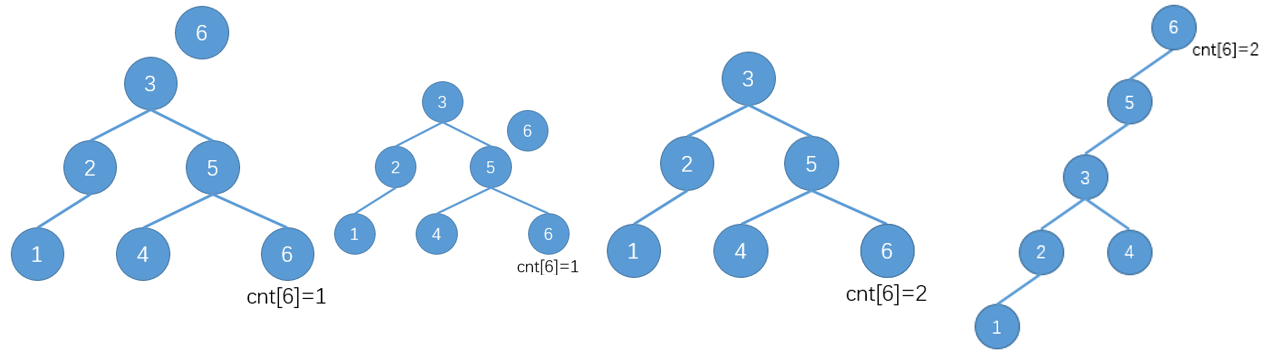
看看代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 | void insert(int x){ if(!root)//如果根节点为空 { whole_size++;//整棵树的大小增加一 sons[whole_size][0]=sons[whole_size][1]=f[whole_size]=0;//默认有一定BST基础,所以这是一个很显然的初始化 root=whole_size;//初始化根节点 sub_size[whole_size]=cnt[whole_size]++;//sub_size 指的是以某节点为根节点的子树的大小,以后会用到的 cnt存储的是某数被插入的次数 val[whole_size]=x;//该节点的数值 return ; } int now=root,fa=0;//从根节点开始走 now表示当前位置 fa表示父亲节点 while(1) { if(x==val[now])//如果找到了数值相等的点,则cnt[now]++ { cnt[now]++; upd(now);//以后会用到的 upd(fa); splay(now);//转到根节点 break; } fa=now; now=sons[now][val[now]<x];//若val[now]<x则会返回1,前往右子树,反之亦然 if(!now)//如果走到了空子树 { whole_size++;//整个splay大小+1 sons[whole_size][0]=sons[whole_size][1]=0;//初始化左右儿子 f[whole_size]=fa;//设置父亲节点 sub_size[whole_size]=cnt[whole_size]=1;//初始化本子树大小 sons[fa][val[fa]<x]=whole_size;//与父节点连接 val[whole_size]=x;//设置该点数值 upd(fa); splay(whole_size);//转到根节点 break; } }} |
删除相较于插入稍微复杂一点,但是也挺好理解的
稍微思考一下如何删除,我们就有了第一个想法
将要删除的点旋转到叶子节点(即,没有子节点的节点),然后直接删除即可
显然这是一种做法,但是不好做,很快我们就发现,前面关于splay的复杂度是基于左旋(zig)右旋(zag)以及左双旋(zig-zig)右双旋(zag-zag)算出来的
既然如此,每个节点将其向下旋转,其复杂度是不好保证的,在实现上也比较麻烦,还有更现实的因素就是看得出来splay的代码是较长的,如果额外去写一个旋转到叶子节点删除的功能就很不优
由此我们就可以很自然的想到,能不能将要删除的点旋转至根节点删除,然后将左右子树合并
这听起来就很优不是吗!(雾霾)
那么删除操作被分成了几块,一是找到该节点,二是旋转至根节点、三是删除节点合并左右子树
1、找到该节点并旋转至根节点
这一步跟插入很像,也就是从根节点出发,目标节点如果大于当前节点则往右子树走,反之亦然
至于旋转至根节点,用前面写好的splay操作直接套就成
看下代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | void find_(int x){ int now=root,ans=0; while(1) { if(x==val[now]) { splay(now); return ; } if(x<val[now]) { now=sons[now][0]; } else if(x>val[now]) { now=sons[now][1]; } }} |
那么……现在那个点转上来了,把他删了怎么合并左右子树呢
先从特殊情况开始思考,如果此时的根节点的cnt>1,那么直接减去1即可
如果根结点有至少一边没有子树,那么直接删除根节点,剩下的部分仍然是一棵splay树
再考虑一下一般情况
首先,左子树的任何一个点肯定都比右子树小,所以可以将左子树最大的一个点旋转至根节点再让右子树的根节点成为该点的右子节点,自此,该点成为了新的根节点
举个例子,我要删除节点6,过程如下
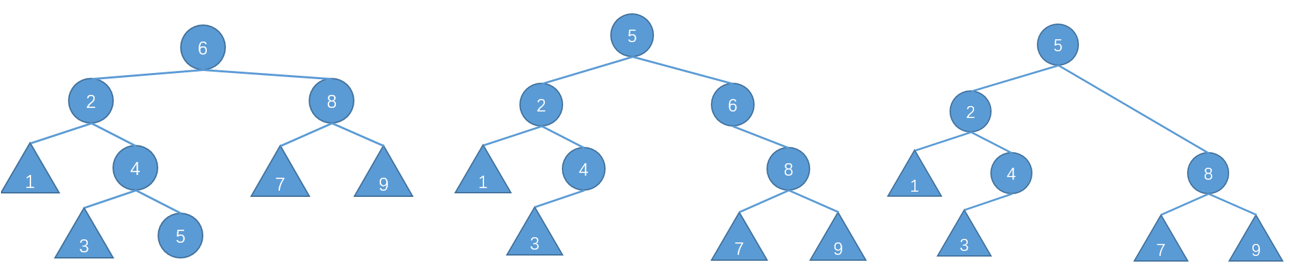
代码实现如下
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 | void find_(int x){ int now=root,ans=0; while(1) { if(x==val[now]) { splay(now); return ; } if(x<val[now]) { now=sons[now][0]; } else if(x>val[now]) { now=sons[now][1]; } }}int find_pre()//找到根节点的左子树上最大的节点 { int now=sons[root][0]; while(sons[now][1]) now=sons[now][1]; return now;}void sclear(int x)//用于删除某节点 { sons[x][0]=sons[x][1]=f[x]=sub_size[x]=cnt[x]=val[x]=0;}void my_delete(int x){ find_(x); //将要删除的节点旋转到根节点 if(cnt[root]>1)//如果根节点的cnt>1说明这个数被插入过不止一次,减去一个即可 { cnt[root]--; upd(root); return ; } //有至少一个子树是空子树 if(!sons[root][0]&&!sons[root][1]) { sclear(root); root=0; return ; } if(!sons[root][0]) { int oldroot=root; root=sons[root][1];//根节点直接变成右子树根节点 f[root]=0; sclear(oldroot); return ; } else if(!sons[root][1]) { int old_root=root; root=sons[root][0];//根节点直接变成左子树根节点 f[root]=0; sclear(old_root); return ; } //合并子树 int left_max=find_pre(),old_root=root;//leftmax指左边最大的点 splay(left_max); //将左子树最大的点旋转到根节点 sons[root][1]=sons[old_root][1];//令原右子树成为新根节点的右子树 f[sons[old_root][1]]=root;//更新父子关系 sclear(old_root);//删除原根节点 upd(root);} |
以上是关于splay最基础的两个操作,现在我们看看splay的其他操作
四、splay的常用功能
参考自P3369【模板】普通平衡树,题目除了插入和删除外还有四种操作
1、查询x数的排名
很显然,作为一个二叉查找树,某节点上的数的排名就是该节点左侧所有节点数的总和+1
如下图的7,就是排名第七位的,因为可以看到其左侧有6个点
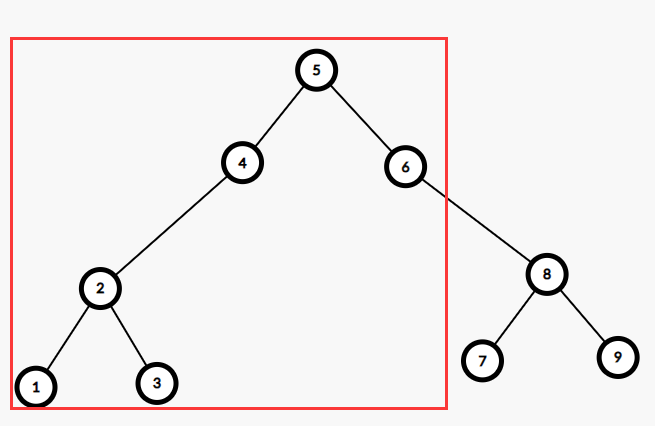
问题来了,那么我们该如何数出其左侧有多少点呢
观察上图,要找到7首先从5出发,再到6,8,7,其中只有8->7是往左子树走了,而应当往右子树 走的节点的左子树都在7的左侧,此外这些应当往右子树走的节点也都在7的左侧,由此我们可以得出统计左侧节点数量的思路
每个点记录以自己为根节点的子树的大小。声明一个num=1的变量用于储存目标节点的排名,每次往右子树走就累加左子树的大小+1,直到找到该节点,将该节点旋转至根节点(图中未展示)

如果你仔细看过前面的代码应该还记得我前面有个upd函数说是后面会有用的,这个upd的作用就是更新某个点的sub_size
1 2 3 4 5 6 7 8 9 10 | void upd(int x){ if(x) { sub_size[x]=cnt[x]; if(sons[x][0]) sub_size[x]+=sub_size[sons[x][0]]; if(sons[x][1]) sub_size[x]+=sub_size[sons[x][1]]; } return ;} |
2、查询排名为x的数
这个操作与上述操作类似,也是要用到子树的大小
具体思路如下
还是从根节点开始,如果当前节点的左子树大小大于x,则前往左子树;
如果当前节点的左子树大小+cnt大于等于x,则当前节点的数值是排名为x的数;
反之前往右子树,并且x=x-左子树大小-该节点的cnt
图例如下,要查找排名为7的数
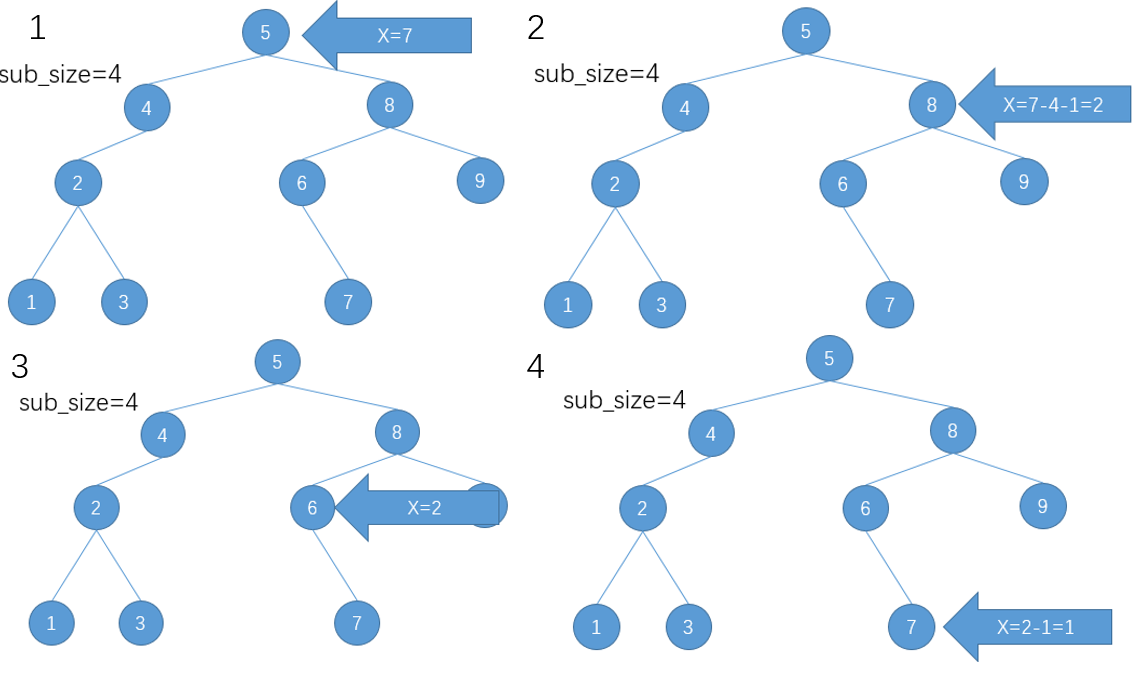
然后将7旋转到根节点,查询就算结束了
3、 求x的前驱(前驱定义为小于x且最大的数)
根据二叉搜索树的性质,前文也提到过,一个节点的左子树的任一数值都小于该节点的数值
那么就可以很轻易地想到,为了实现这个操作可以先找到x的节点,旋转到根节点,然后再从它的左子树中找到最大值
紧接着我们发现x不一定在树中,于是我们可以先加入x,并旋转至根节点,然后再找到左子树最大值,这便是x的前驱,随后删除x
插入、删除操作前文都提过了,这里附上找左子树最大值的代码
1 2 3 4 5 6 | int find_pre(){ int now=sons[root][0]; while(sons[now][1])now=sons[now][1]; return now; } |
4、求x的后继(后继定义为大于x且最小的数)
同上,唯一的区别就是这里要求右子树的最小值
附上代码
1 2 3 4 5 6 | int find_suffix(){ int now=sons[root][1]; while(sons[now][0]) now=sons[now][0]; return now;} |
至此,我已经讲完了关于splay的六种常规操作了
插入x数
删除 x 数(若有多个相同的数,应只删除一个)
查询 x 数的排名(排名定义为比当前数小的数的个数+1 )
查询排名为 x 的数
求x 的前驱(前驱定义为小于 x,且最大的数)
求 x 的后继(后继定义为大于 x,且最小的数)
最后附上完整代码(撒花!)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 | #include<bits/stdc++.h>#define int long longusing namespace std; const int mn=1000005;int f[mn],cnt[mn],val[mn],sons[mn][2],sub_size[mn],whole_size,root;int read(){ int res=0,k=1; char c=getchar(); while(!isdigit(c)) { if(c=='-') k=-1; c=getchar(); } while(isdigit(c)) { res=(res<<1)+(res<<3)+c-48; c=getchar(); } return res*k;}void sclear(int x){ sons[x][0]=sons[x][1]=f[x]=sub_size[x]=cnt[x]=val[x]=0;}bool get(int x){ return sons[f[x]][1]==x;}void upd(int x){ if(x) { sub_size[x]=cnt[x]; if(sons[x][0]) sub_size[x]+=sub_size[sons[x][0]]; if(sons[x][1]) sub_size[x]+=sub_size[sons[x][1]]; } return ;}void rotate(int x){ int fa=f[x],grand=f[fa],son1=get(x),son2=(son1+1)%2;//f存储某节点的父节点编号 get是查找该节点是其父节点的左子节点还是右子节点 0为左 1为右 sons[fa][son1]=sons[x][son2];//将子节点挂到父节点上去 f[sons[fa][son1]]=fa; sons[x][son2]=fa; f[fa]=x;//更新关系 f[x]=grand; if(grand) { sons[grand][sons[grand][1]==fa]=x;//如果有祖父节点要令祖父节点成为该节点的父节点 } upd(fa); upd(x);}void splay(int x){ for(int fa;fa=f[x];rotate(x))//旋转直到x成为根节点 { if(f[fa]) rotate((get(x)==get(fa))?fa:x);//双旋 } root=x;//更新根节点 }void insert(int x){ if(!root)//如果根节点为空 { whole_size++;//整棵树的大小增加一 sons[whole_size][0]=sons[whole_size][1]=f[whole_size]=0;//默认有一定BST基础,所以这是一个很显然的初始化 root=whole_size;//初始化根节点 sub_size[whole_size]=cnt[whole_size]++;//sub_size 指的是以某节点为根节点的子树的大小,以后会用到的 cnt存储的是某数被插入的次数 val[whole_size]=x;//该节点的数值 return ; } int now=root,fa=0;//从根节点开始走 now表示当前位置 fa表示父亲节点 while(1) { if(x==val[now])//如果找到了数值相等的点,则cnt[now]++ { cnt[now]++; upd(now);//以后会用到的 upd(fa); splay(now);//转到根节点 break; } fa=now; now=sons[now][val[now]<x];//若val[now]<x则会返回1,前往右子树,反之亦然 if(!now)//如果走到了空子树 { whole_size++;//整个splay大小+1 sons[whole_size][0]=sons[whole_size][1]=0;//初始化左右儿子 f[whole_size]=fa;//设置父亲节点 sub_size[whole_size]=cnt[whole_size]=1;//初始化本子树大小 sons[fa][val[fa]<x]=whole_size;//与父节点连接 val[whole_size]=x;//设置该点数值 upd(fa); splay(whole_size);//转到根节点 break; } }}int find_num(int x){ int now=root; while(1) { if(sons[now][0]&&x<=sub_size[sons[now][0]]) now=sons[now][0]; else { int temp=(sons[now][0]?sub_size[sons[now][0]]:0)+cnt[now];//因为有重复插入的情况,所以这里不是+1而是+cnt if(x<=temp) { splay(now); return val[now]; } x=x-temp; now=sons[now][1]; } }}int find_rank(int x){ int now=root,ans=0; while(1) { if(x<val[now]) { now=sons[now][0]; } else { ans+=(sons[now][0]?sub_size[sons[now][0]]:0); if(x<=val[now]) { splay(now); return ans+1; } ans+=cnt[now]; now=sons[now][1]; } }}int find_pre(){ int now=sons[root][0]; while(sons[now][1])now=sons[now][1]; return now; }int find_suffix(){ int now=sons[root][1]; while(sons[now][0]) now=sons[now][0]; return now;}void my_delete(int x){ find_rank(x); if(cnt[root]>1) { cnt[root]--; upd(root); return ; } if(!sons[root][0]&&!sons[root][1]) { sclear(root); root=0; return ; } if(!sons[root][0]) { int oldroot=root; root=sons[root][1]; f[root]=0; sclear(oldroot); return ; } else if(!sons[root][1]) { int old_root=root; root=sons[root][0]; f[root]=0; sclear(old_root); return ; } int left_max=find_pre(),old_root=root; splay(left_max); sons[root][1]=sons[old_root][1]; f[sons[old_root][1]]=root; sclear(old_root); upd(root);}signed main(){ //freopen("in.txt","r",stdin); int m,num,be_dealt; cin>>m; for(int i=1;i<=m;i++) { num=read(); be_dealt=read(); switch(num) { case 1:insert(be_dealt);break; case 2:my_delete(be_dealt);break; case 3:printf("%d\n",find_rank(be_dealt));break; case 4:printf("%d\n",find_num(be_dealt));break; case 5:insert(be_dealt);printf("%d\n",val[find_pre()]);my_delete(be_dealt);break; case 6:insert(be_dealt);printf("%d\n",val[find_suffix()]);my_delete(be_dealt);break; } } return 0;} |
五、后记
写这篇blog真的花费了我很长的时间,splay本身的代码就比较长,但我没想到写成blog更长----这大概是我写过的blog中最长的一篇,耗时和篇幅都是最长。
splay的核心思想在于如何用splay保证「平衡」——显然,也是最难理解的。大部分平衡树是通过「旋转」来保持平衡性质的。因此,在这篇文章里,我尽可能地说清楚什么是左旋、什么是右旋。如果没有理解旋转,那平衡树就是没学。
平衡树作为OI的常规考点其重要性是不言而喻的,而splay作为一种功能非常强大的平衡树,学好splay定能让你在各大竞赛中如虎添翼
预祝所有oier 在新学年rp++





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· winform 绘制太阳,地球,月球 运作规律
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 超详细:普通电脑也行Windows部署deepseek R1训练数据并当服务器共享给他人
· AI与.NET技术实操系列(五):向量存储与相似性搜索在 .NET 中的实现