孤立森林（IForest）代码实现及与PyOD对比

　　孤立森林（Isolation Forest）是经典的异常检测算法（论文网址）。本文用python对其进行实现，以及与常用的异常检测包PyOD进行效果对比。

　　简单来说，孤立森林（IForest）中包含若干孤立树（ITree），每颗树的创建是独立的，与其它树无关。假设数据集包含$n$个样本，每个样本都包含$m$个实数特征。在创建每颗孤立树时，根节点首先包含所有$n$个样本。对于每个节点，随机抽取一个特征，在该特征的最大与最小值之间随机取一数$p$，将小于$p$的样本划分在左子节点，将大于$p$的样本划分在右子节点。划分直到叶节点只包含一个样本，或达到树高为止，文中树高定义为$\text{ceil}(\log_2n)$。构建好IForest后的测试阶段，就是计算样本在每颗孤立树上被划分到叶节点的平均路径长度，作为计算异常分数的依据。显然，划分路径越短，异常的可能性越高。

　　实现代码如下：

#%% 函数定义
import torch
import numpy as np
import matplotlib.pyplot as plt

def iTree(X:torch.Tensor, e, l):
    # X数据集，e当前路径长，l树高最大值
    if e >= l or len(X) <= 1:
        return [0, len(X)] # 0 非叶子节点
    q = np.random.randint(0, len(X[0]))
    M, m = X[:, q].max(), X[:, q].min()
    p = np.random.rand()*(M - m) + m
    lchild = iTree(X[X[:,q] < p,:], e+1, l)
    rchild = iTree(X[X[:,q] >= p,:], e+1, l)
    return [1, lchild, rchild, q, p]
def c(n):
    c = 0 if n == 1 else 2*(np.log(n-1)+0.5772156649) - (2*(n-1)/n)
    return c
def PathLength(x, T, e):
    # x样本，T树，e当前路径长
    if T[0] == 0:
        return e + c(T[1])
    if x[T[3]] < T[4]:
        return PathLength(x, T[1], e+1)
    return PathLength(x, T[2], e+1)
def myIForest(X, t, psi):
    # X训练集，t树数量，psi子采样
    Ts = []
    l = np.ceil(np.log(psi))
    for i in range(t):
        x_i = np.random.choice(range(len(X)), [psi], replace=False)
        Ts .append(iTree(X[x_i], 0, l))
    return Ts
def anomalyScore(x, Ts, psi):
    length = 0
    for T in Ts:
        length += PathLength(x, T, 0)
    length /= len(Ts)
    s = 2**(-length/c(psi))
    return s
#%% 定义正常分布、超参数、绘图矩阵
torch.manual_seed(0)
np.random.seed(0)
points = torch.randn([512, 2]) 
points[-80:] = torch.randn([80, 2])/3+4
t, psi = 100, 256
x, y = np.arange(-4.5, 5.5, 0.1), np.arange(-4.5, 5.5, 0.1)
X, Y = np.meshgrid(x, y)
XY = np.stack([X,Y], -1)
Z = np.zeros_like(X)
#%% 自定义孤立森林、异常值可视化、决策边界
myTs = myIForest(points, t, psi)
for i in range(XY.shape[0]):
    for j in range(XY.shape[1]):
        Z[i,j] = anomalyScore(XY[i, j], myTs, psi)
plt.plot(points[:,0],points[:,1], '.', c = "purple", alpha = 0.3)
plt.contourf(X,Y,Z)
cont = plt.contour(X,Y,Z, levels=[0.55])
plt.clabel(cont, inline=True, fontsize=10)
plt.show()
#%% pyOD孤立森林、异常值可视化、决策边界
from pyod.models.iforest import IForest
ifor = IForest(t, psi, 0.1, random_state=0)
ifor.fit(points)
h, w = XY.shape[0], XY.shape[1]
XY = XY.reshape(-1, 2)
Z = Z.reshape(-1)
Z = ifor.decision_function(XY)
Z = Z.reshape(h, w)
XY = XY.reshape(h,w,2)

plt.plot(points[:,0],points[:,1], '.', c = "purple", alpha = 0.3)
plt.contourf(X,Y,Z)
cont = plt.contour(X,Y,Z, levels=[0]) #决策边界为0
plt.clabel(cont, inline=True, fontsize=10)
plt.show()

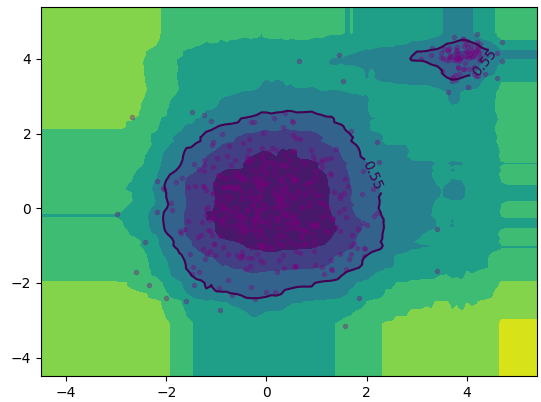
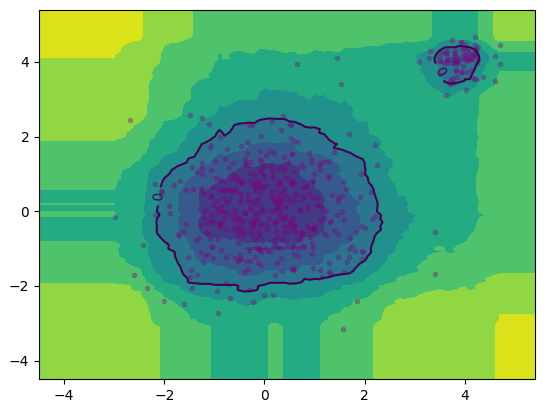
　　自定义孤立森林和PyOD定义的孤立森林可视化结果分别如下左右图所示：

　　效果相似。其中自定义代码完全按照论文伪代码实现，使用二叉搜索树的平均失败搜索长度进行归一化，异常分数取值$(0,1)$。PyOD的异常分数取值似乎是$(-1,1)$，以0为区分阈值，即把自定义比例的正常样本的异常分数设置为小于0，大于0则为异常样本。此处设置10%为异常，90%正常。另外，由于自定义代码没有使用并行策略，运行时间会比PyOD长得多。