在matlab中使用遗传算法执行最优化
遗传算法是一种通用的最优化方法,具体原理可以看:遗传算法详解与实验。下面记录在Matlab中如何使用遗传算法来做优化。
用法
调用方式如下:
1 x = ga(fun,nvars) 2 x = ga(fun,nvars,A,b) 3 x = ga(fun,nvars,A,b,Aeq,beq) 4 x = ga(fun,nvars,A,b,Aeq,beq,lb,ub) 5 x = ga(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon) 6 x = ga(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon,options) 7 x = ga(fun,nvars,A,b,[],[],lb,ub,nonlcon,IntCon) 8 x = ga(fun,nvars,A,b,[],[],lb,ub,nonlcon,IntCon,options) 9 x = ga(problem) 10 [x,fval] = ga(___) 11 [x,fval,exitflag,output] = ga(___) 12 [x,fval,exitflag,output,population,scores] = ga(___)
参数解释
fun: 要执行最优化的函数,用于输入待优化变量$x$。只能包含一个参数,可以是单个标量,也可以是向量。输出一个标量。
nvars: 最优化函数传入向量的元素数量。
A, b: 线性不等式约束的系数。即待优化变量$x$要满足$A\cdot x \le b$。
Aeq, beq: 线性等式约束的系数。即待优化变量$x$要满足$Aeq\cdot x = beq$。
lb, ub: 传入向量的取值范围。即待优化变量$x$要满足$lb\le x\le ub$。
nonlcon: 定义非线性不等式约束和等式约束的函数。该函数只能包含一个参数用于接受待优化变量$x$,然后输出不等式约束值$C(x)$和等式约束值$Ceq(x)$。约束$x$满足$C(x)\le 0$和$Ceq(x)=0$。
IntCon: 限制待优化参数为整数,传入需要限制为整数的待优化参数的位置。如对于3维变量$x$,设置IntCon为$[1,3]$表示第一和第三维的元素被限制为整数。
options: 遗传算法的设置,设置初始化、迭代次数、种群大小等。具体请看链接。
[]: 对于不想使用的约束,可以用中括号[]省略。
传出参数
x: 最优化后的变量。
fval: $x$对应的函数值。
exitflag: 遗传算法结束标志,一个整数。分别解释如下:

output: 遗传算法的优化过程信息。
population: 遗传迭代最后的种群。数组每行表示一个函数变量。
scores: 最后种群的个体值。也就是数组中各个变量的函数值。
例子
首先定义待优化函数:
1 function outp = func(varargin) 2 narginchk(1,2); 3 if nargin == 1 4 x = varargin{1}(1); 5 y = varargin{1}(2); 6 elseif nargin == 2 7 x = varargin{1}; 8 y = varargin{2}; 9 end 10 outp = 2*exp((-(x+3).^2-(y-3).^2)/10) + 1.2*exp((-(x-3).^2-(y+3).^2)/10) + exp(-cos(3*x)-sin(3*y)); 11 outp = -outp; 12 end
然后是该函数的可视化和优化:
1 %% 函数可视化 2 x = linspace(-5,0,500); 3 y = linspace(0,5,500); 4 [X, Y] = meshgrid(x, y); 5 6 Z = func(X, Y); 7 mesh (X,Y,Z); 8 9 %% 优化 10 [x, f] = ga(@func, 2);
通过可视化可以看到最小值大概在$(-3.14, 3.66)$附近:
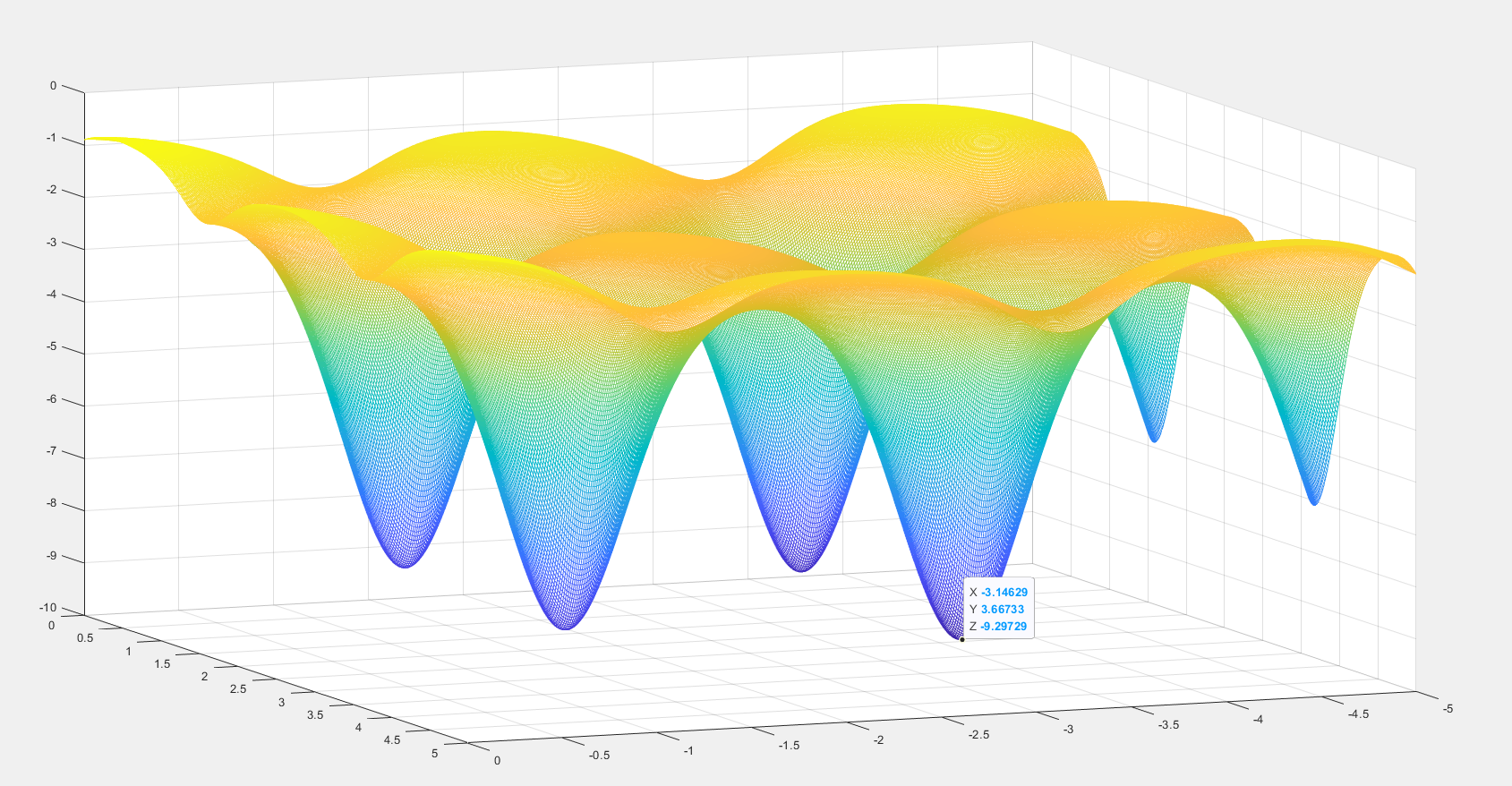
优化结果也是如此: