分组卷积和深度可分离卷积

分组卷积

　　之间看分组卷积示意图。

　　不分组：

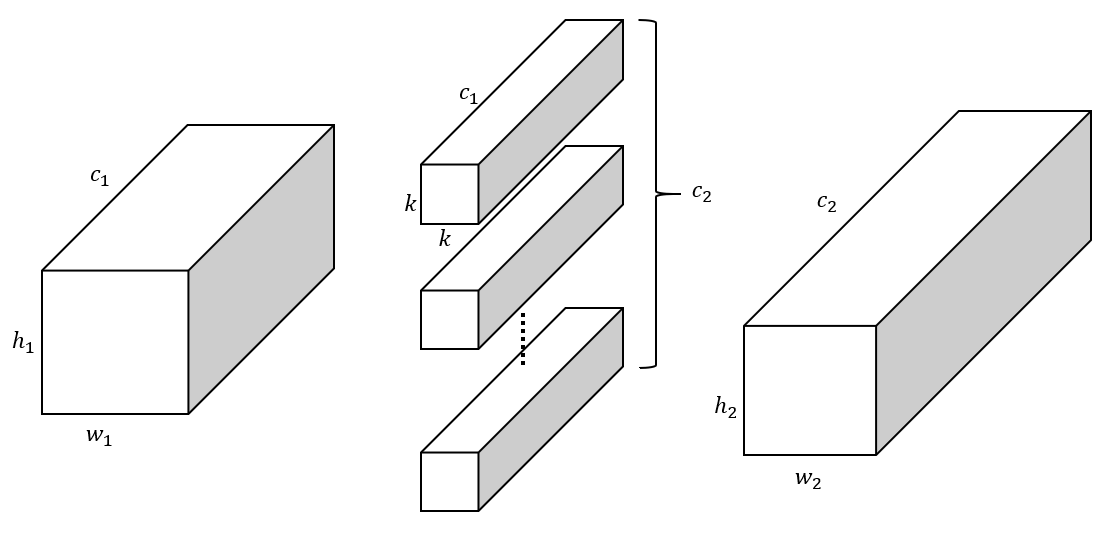
　　分两组：

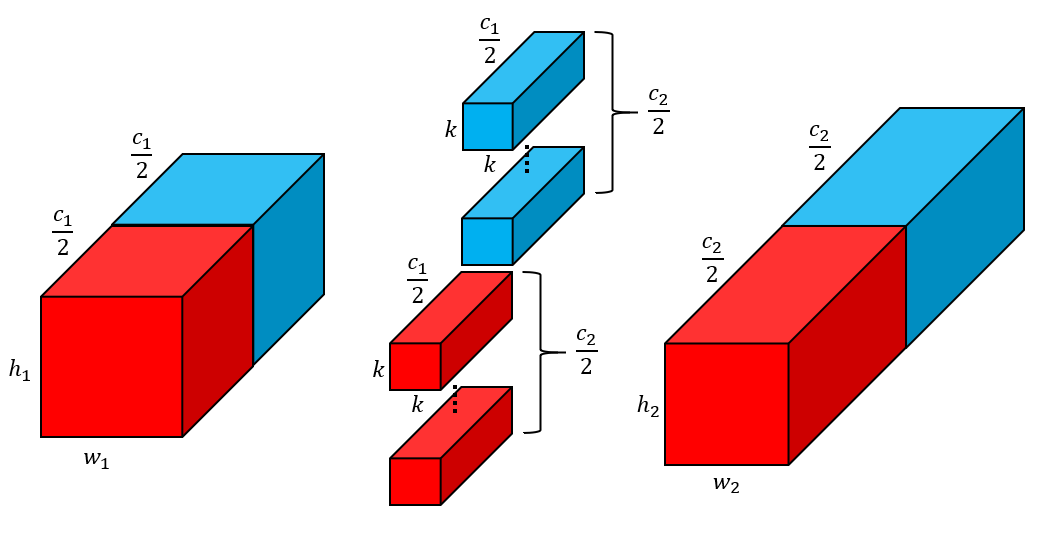
　　分四组：

　　以此类推。当然，以上都是均匀分组的，不均分也是可以的。至于分组卷积有什么好处，很明显，可以节省参数量。假设不使用分组时，卷积核的参数量为：

$n = k^2c_1c_2$

　　其中$k,c_1,c_2$分别表示卷积核宽度，输入通道数，输出通道数。如果使用分组卷积，分为$m$组，则卷积核参数量为：

$\displaystyle n = mk^2\frac{c_1}{m}\frac{c_2}{m} = \frac{k^2c_1c_2}{m}$

　　也就是说分几组，参数量就为原来的几分之几。当然偏置值是不会被节省的，都是$c_2$个。分组卷积时，每个分组对其它分组的特征图不可见，这实际上就等价于把网络进行分支，也就是把输入的特征图以通道维度拆开来分别进行卷积，然后再将卷积结果拼接起来。分几组就等于分几个支。

　　分组卷积.ppt

深度可分离卷积

　　深度可分离卷积（depthwise separable convolution）分为深度卷积（Depth-wise Convolution）和逐点卷积（Point-wise Convolution）两步：

　　1、深度卷积就是把$h\times w\times c$的特征图$F$以通道维度分开，得到$c$个$h\times w\times 1$的特征图，然后使用$c$个$k\times k \times 1\times 1$的卷积核分别对这$c$个特征图进行卷积，得到$c$个$h'\times w'\times 1$的特征图，最后将他们按原来的顺序连接起来得到$h'\times w'\times c$的特征图$F'$。

　　2、逐点卷积就是用$1\times 1\times c\times c_1$的卷积对$F'$进行卷积，得到$h'\times w'\times c_1$的最终结果。

　　其中深度卷积不使用偏执值，逐点卷积使用了偏执值。整个流程图如下：

　　根据以上流程，可以计算出深度可分离卷积所需的参数量为（加的1为偏执值参数量）：

$n = k^2c+(c+1)c_1$