协方差与联合概率密度的关系、协方差的几何意义
以二维正态分布来举例。当方差不变,而协方差变化时,分布沿着长宽比等于两个方差之比的矩阵逐渐变窄。如下图所示:
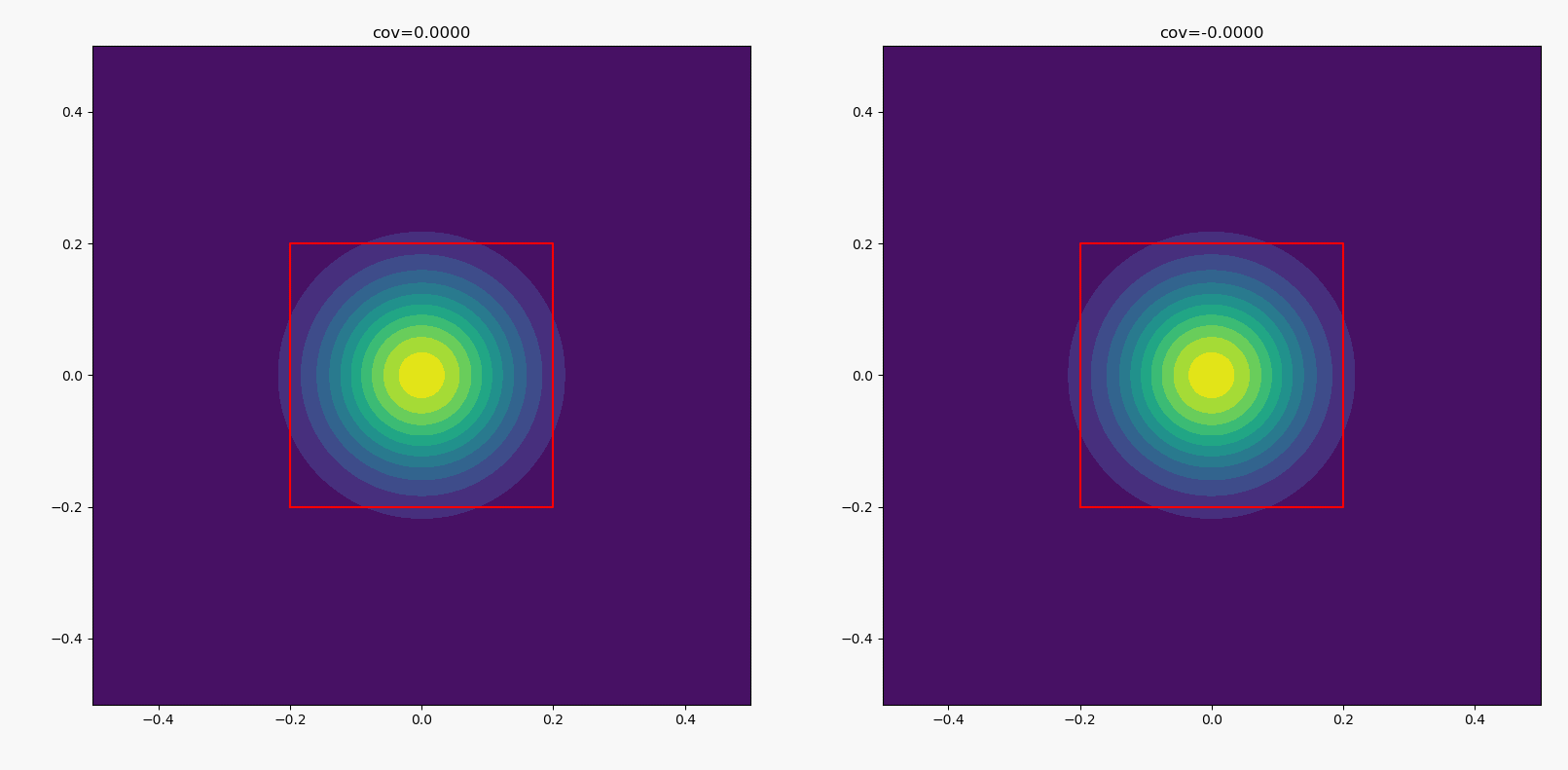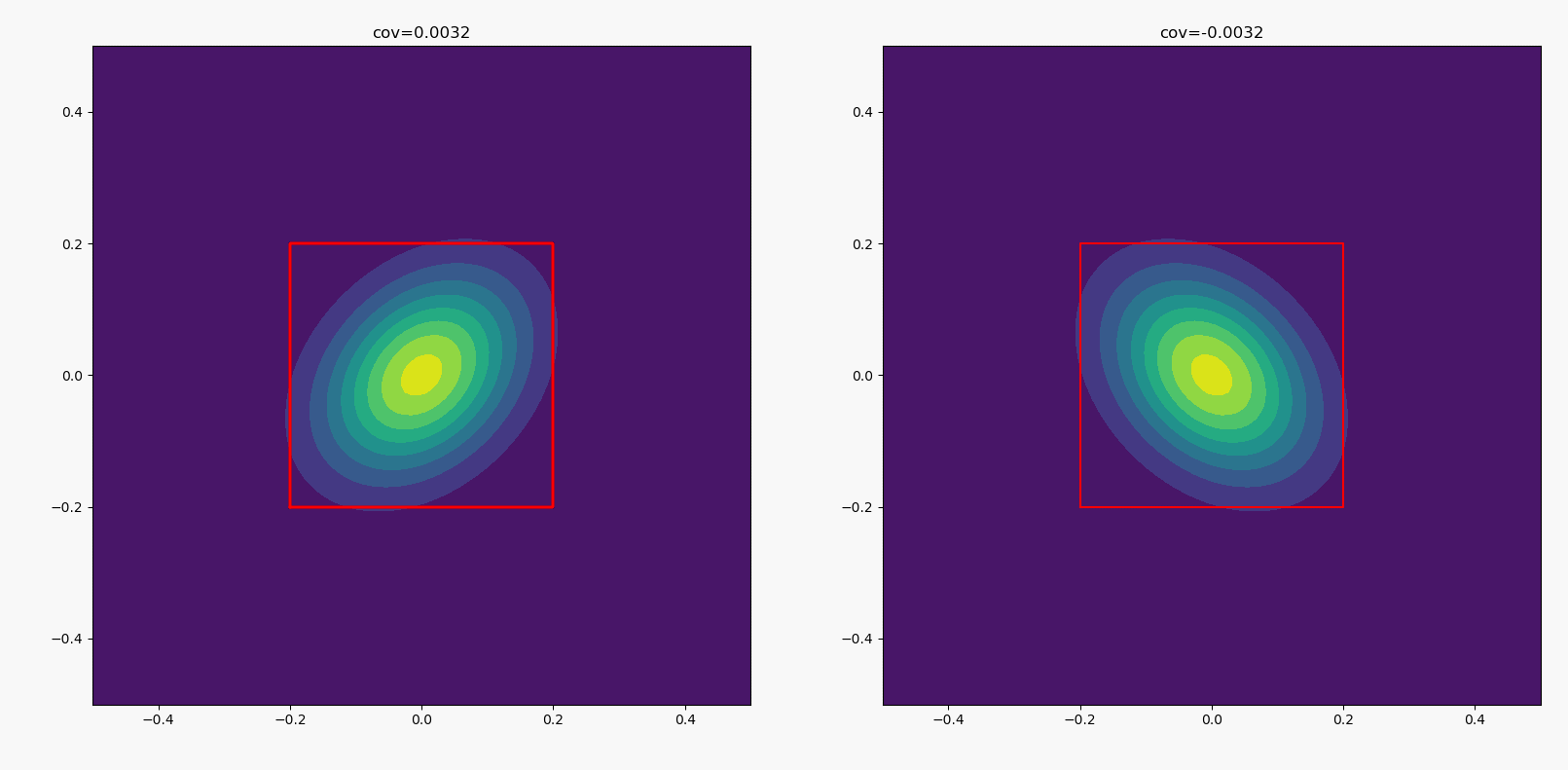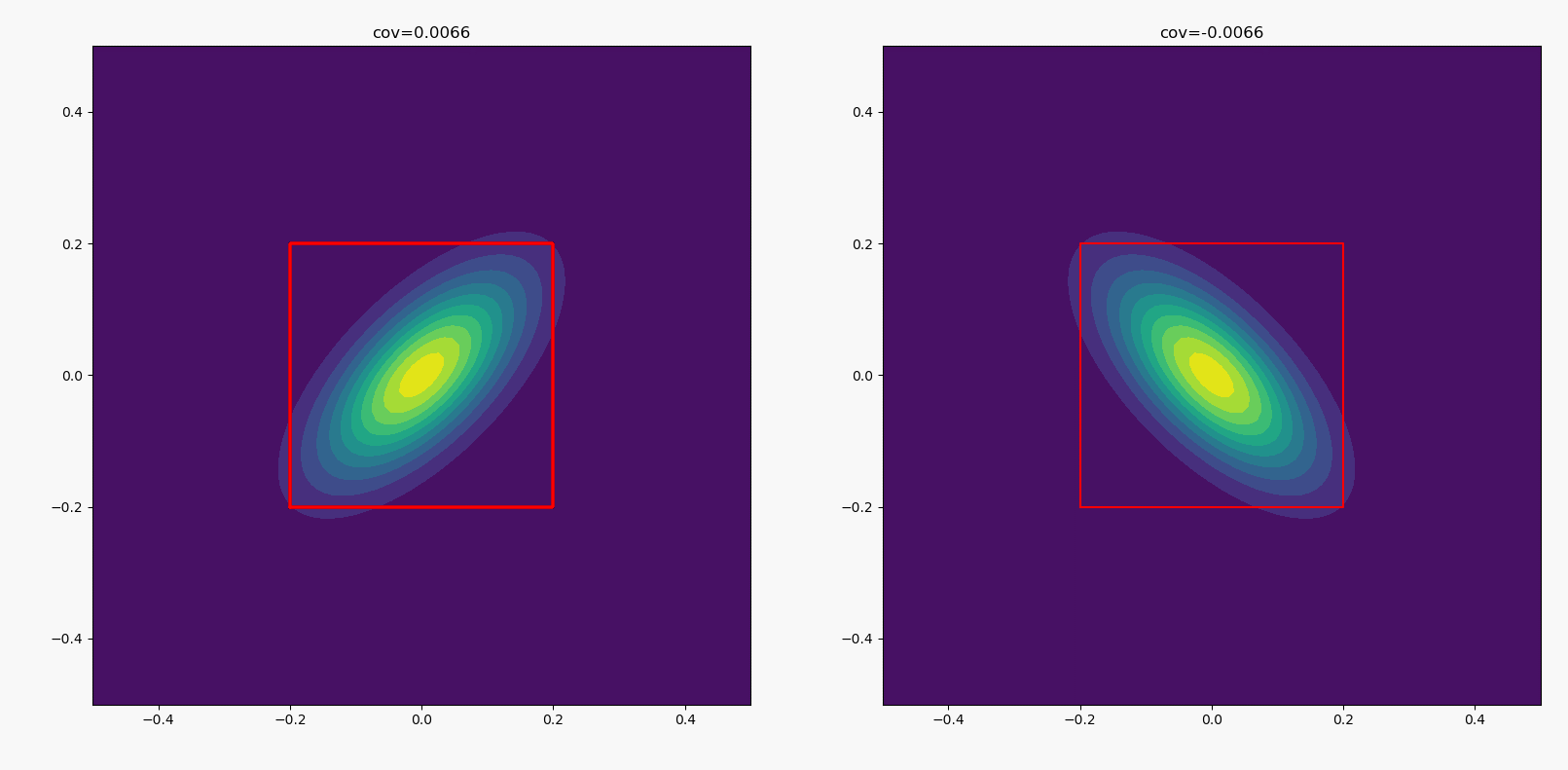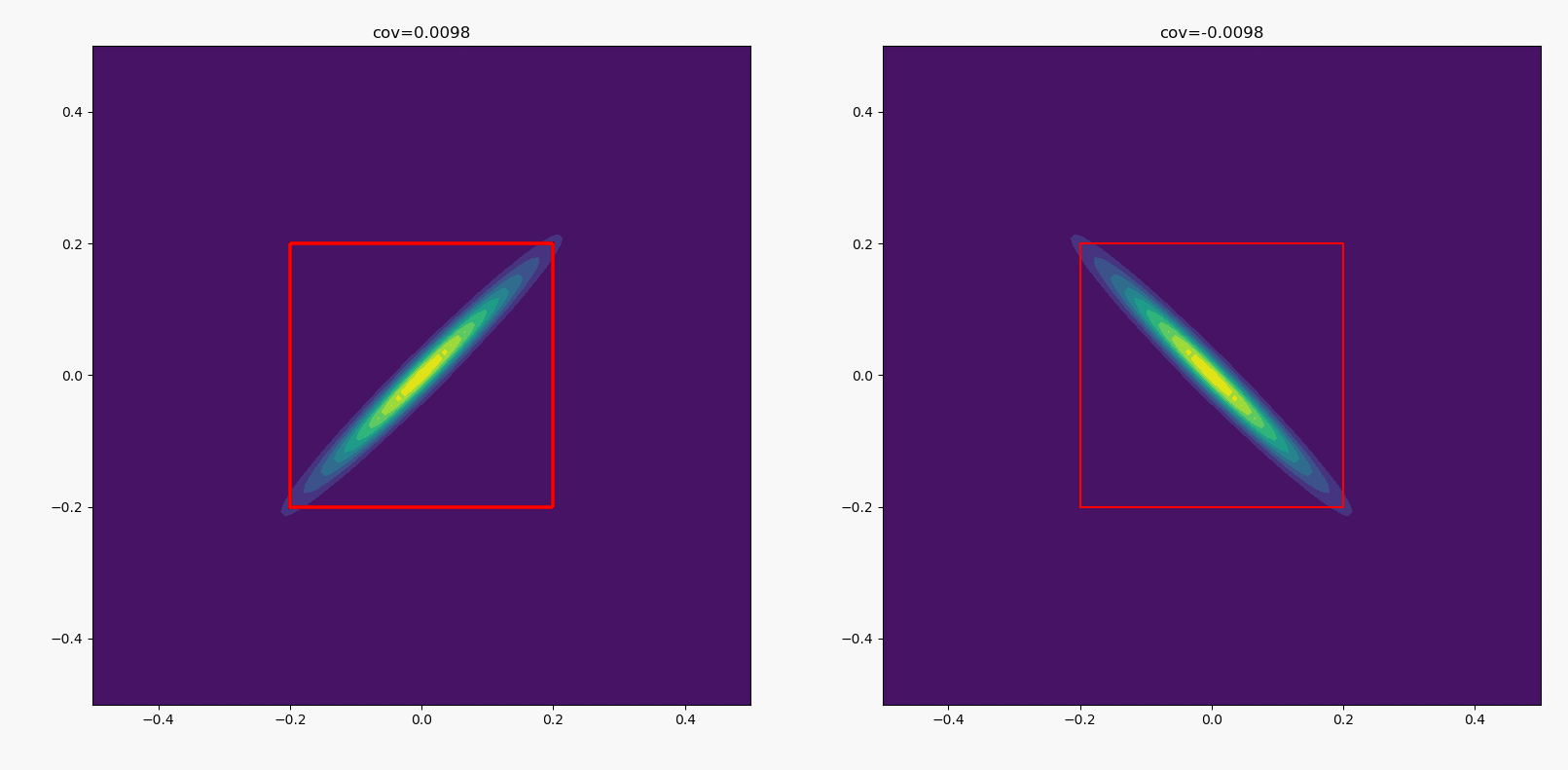
两个分布的标准差都为0.1,均值都为0,协方差左边从0一直上升到0.01,右边从0下降到-0.01。
看了这个图,有人可能会问,随着协方差的变化,同一高度的椭圆等高线是否始终与矩形相切。看起来好像是这样的,然而并没有。具体证明就是高中的解析几何题,不赘述(其实仔细看动图也能看出来并没有)。
当协方差和方差一起变化时,分布变化如下:
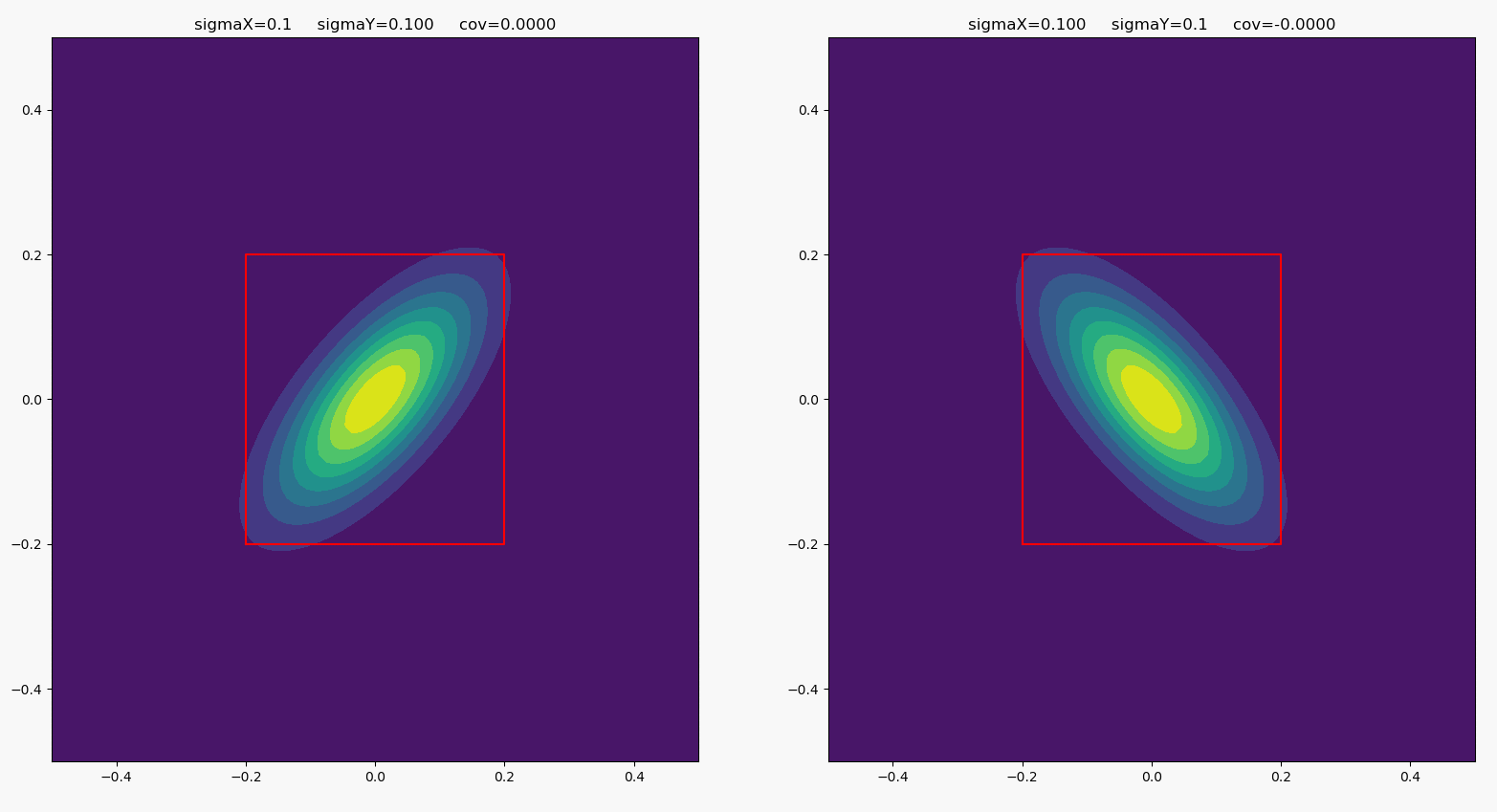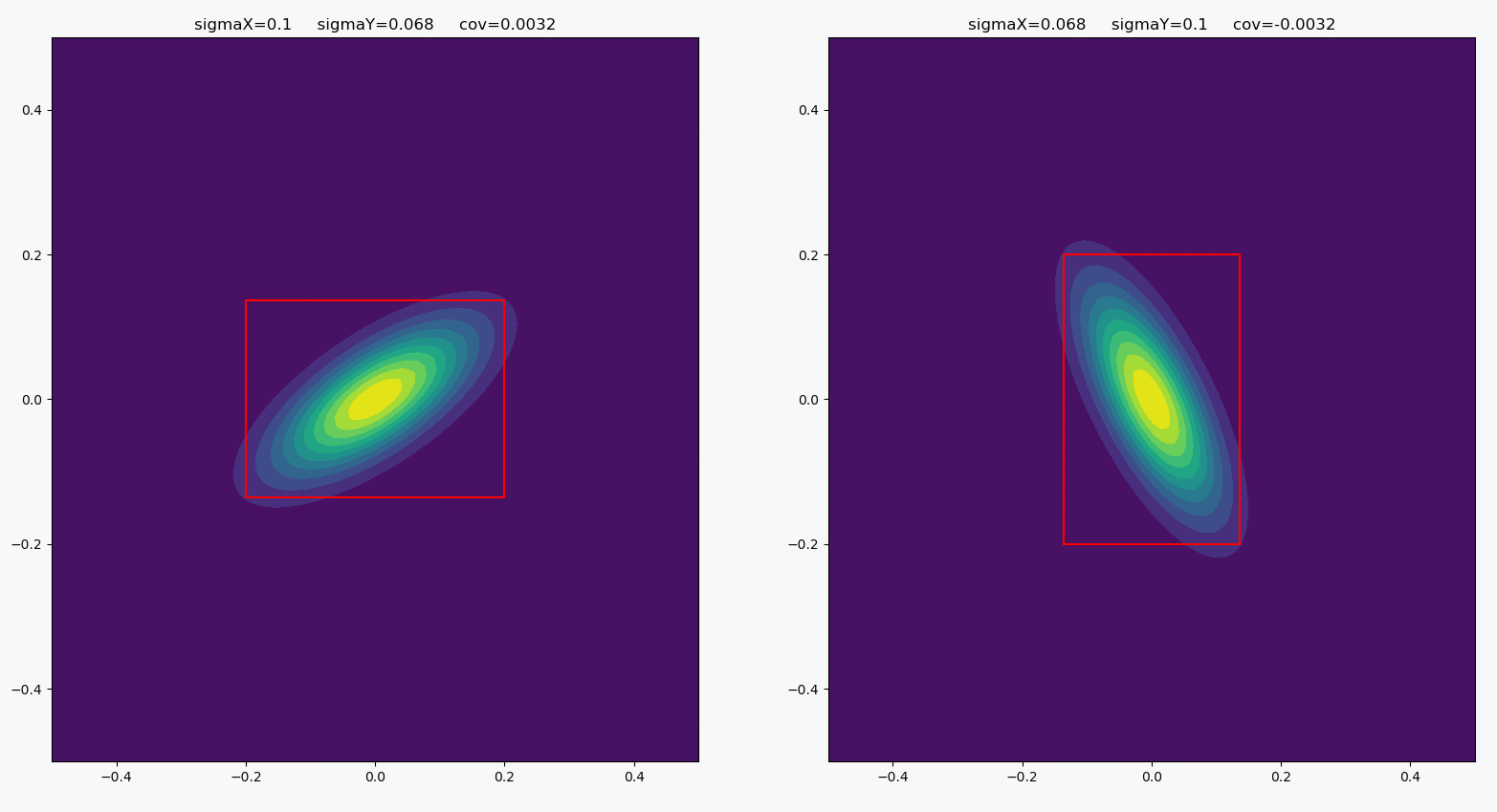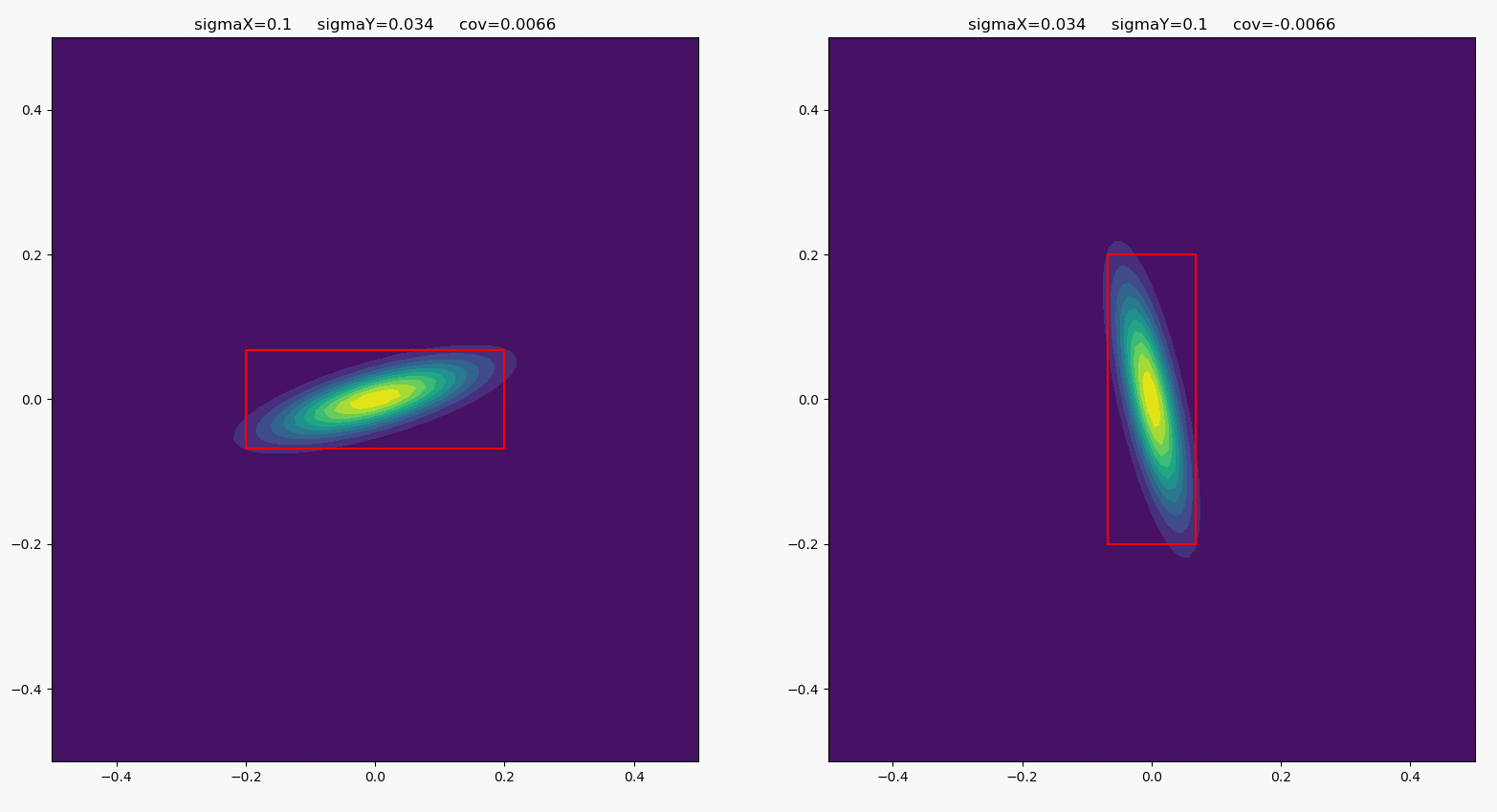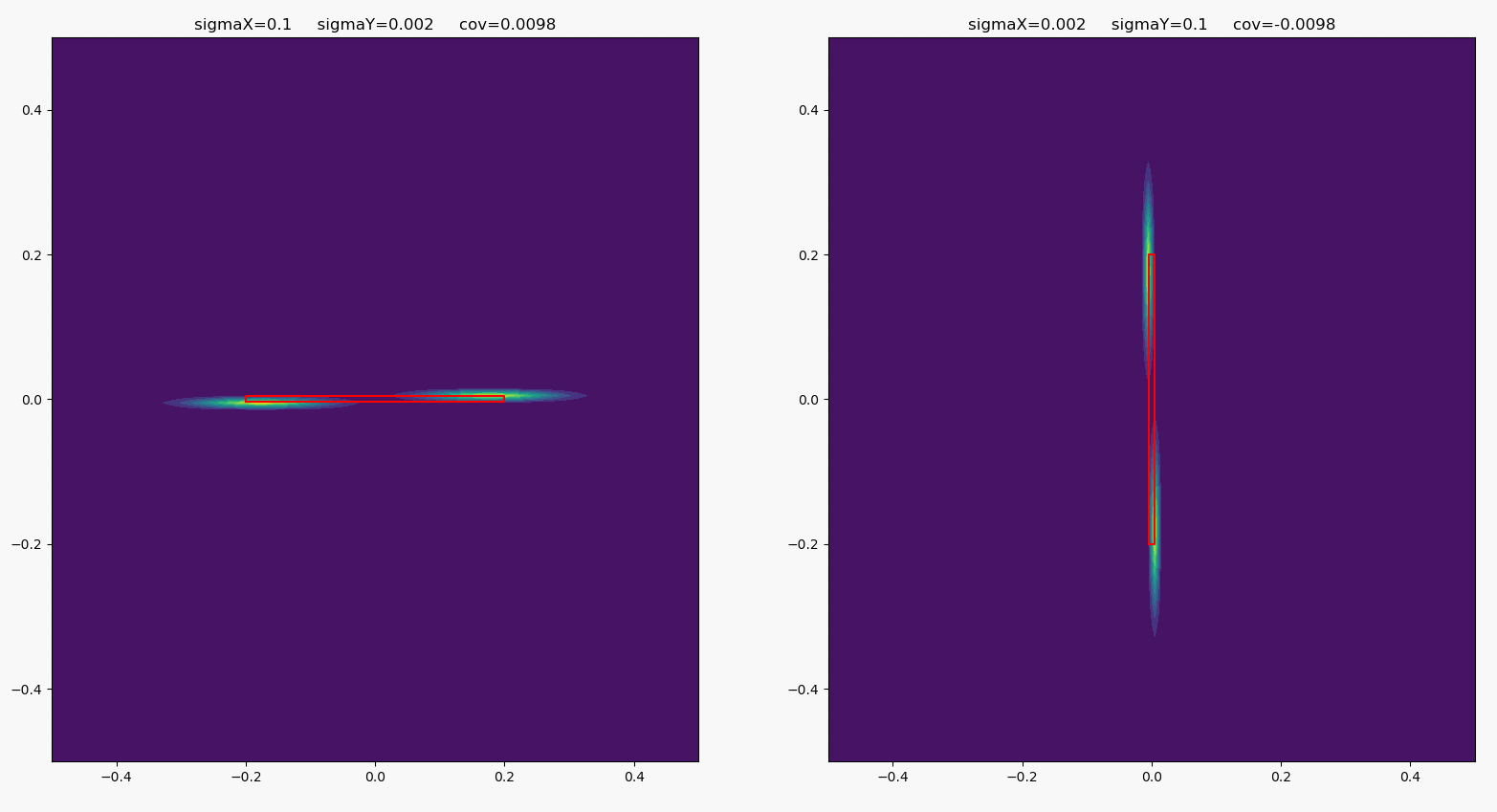
其中的矩形长宽比同样等于横纵随机变量的方差之比。
经过以上观察,我们可以总结出,方差决定了联合分布的“倾斜度”,协方差决定了联合分布的“宽度”。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号