Wasserstein GAN
WGAN论文指出,原始GAN以JS、KL散度作为损失容易导致生成器梯度消失,他们提出了一种新的损失函数——Wasserstein 距离,很大程度上解决了GAN训练难的问题。
原始GAN的损失函数的缺陷
当两个分布之间重叠很小,或者说,两个分布的概率密度同时大于0的区域在整个分布的占比几乎为0时(无穷小,但还不是0),随着分布之间的靠拢,用于衡量分布之间差异的KL、JS散度几乎没有变化,也就是梯度十分小。而真实分布与生成分布在训练开始时的重叠就是十分小的(证明要用到拓扑学和测度论,直观理解请看后面的知乎链接),并且由于我们只能用部分样本代替真实分布与生成分布来训练,这种情况就更加严重了,从而解释了生成器训练时梯度消失的问题。
论文举了个简单的例子用于理解。如下图所示,$P_1,P_2$表示两个二维空间中的均匀分布:
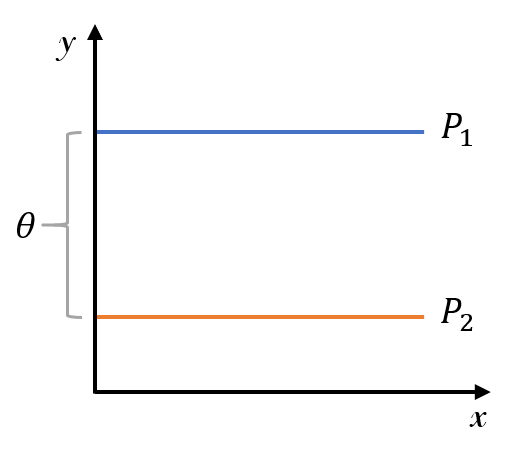
如果我们要将$P_1$移动到$P_2$,就要计算两个分布之间的差异,然后再计算梯度来减小差异。下面分别以KL散度、JS散度和Wasserstein 距离作为差异指标,计算得到:
\begin{equation*} \begin{aligned} &KL(P_1||P_2) = KL(P_2||P_1) = \left\{ \begin{aligned} &+\infty,&\theta \ne 0\\ &0,&\theta = 0 \end{aligned} \right.\\ &JS(P_1||P_2) = \left\{ \begin{aligned} &\log 2,&\theta \ne 0\\ &0,&\theta = 0 \end{aligned} \right. \\ &W(P_1,P_2) = |\theta| \end{aligned} \end{equation*}
看得出,KL、JS散度的梯度是0,没法训练。而Wasserstein距离则计算出一个符合常识的距离指标,可以计算梯度控制$P_1$向$P_2$靠近。
当然以上只是简单的举例,你一眼就能看出$P_1,P_2$之间的距离用$\theta$表示更合理。下面开始具体介绍Wasserstein 距离,以及以它为损失函数的WGAN。
Wasserstein距离与WGAN
Wasserstein距离又叫Earth-Mover(EM)距离。对于真实分布$P_r$和生成分布$P_g$,Wasserstein距离$W(P_r,P_g)$定义如下:
\begin{equation} \begin{aligned} W(P_r,P_g) = \inf\limits_{\gamma\sim\Pi(P_r,P_g)}\mathbb{E}_{(x,y)\sim\gamma}\left(||x-y||\right) \end{aligned} \end{equation}
其中$\Pi(P_r,P_g)$表示$P_r$和$P_g$组合起来的所有可能的联合分布的集合,集合中的每个联合分布的边缘分布都为$P_r$和$P_g$。对于每一个可能的联合分布$\gamma$而言,可以从中采样$(x,y)\sim \gamma$得到一个真实样本$x$和一个生成样本$y$,并算出这对样本的距离$||x-y||$,所以可以计算该联合分布$\gamma$下样本对距离的期望值$\mathbb{E}_{(x,y)\sim\gamma}\left(||x-y||\right)$。我们可以直观理解为,通过对所有样本进行“搬迁”,使用$\gamma$作为搬迁方式将分布$P_r$转变为分布$P_g$所需的消耗。而所有这些搬迁方式的下界$\inf\limits_{\gamma\sim\Pi(P_r,P_g)}\mathbb{E}_{(x,y)\sim\gamma}\left(||x-y||\right)$,也就是消耗最小的,就定义为Wasserstein距离。
Wasserstein距离是比JS、KL散度在定义上更弱的差异评估标准,即便两个分布没有重叠,Wasserstein距离仍然能够反映它们的远近。但是上面的定义是不能用作GAN的损失的,于是论文用了一个已有的定理把它变换为如下形式(推导过程用到了拓扑学和测度论,先挖个坑,以后学了再回来填):
\begin{equation} \begin{aligned} W(P_r,P_g) = \frac{1}{K}\sup\limits_{|f|_L\le K}\mathbb{E}_{x\sim P_r}[f(x)] -\mathbb{E}_{x\sim P_g}[f(x)] \end{aligned} \end{equation}
其中$|f|_L\le K$表示,对于常数$K$,连续函数$f$定义域内的任意两个元素$x_1$和$x_2$都应满足
\begin{equation} \begin{aligned}|f(x_1)-f(x_2)|\le K|x_1-x_2|\end{aligned} \end{equation}
定义域为实数域时,上式所表达的就是$|f'(x)|\le K$。这个限制叫Lipschitz连续。为了可以在神经网络中应用,进一步近似变换$(2)$式为如下形式
\begin{equation} \begin{aligned} K \cdot W(P_r,P_g) \approx \max\limits_{w:|f_w|_L\le K}\mathbb{E}_{x\sim P_r}[f_w(x)] -\mathbb{E}_{x\sim P_g}[f_w(x)] \end{aligned} \end{equation}
将所有可能的函数,用一个带参数的函数来表示,通过改变参数来表示这些可能的函数。虽然不能囊括所有可能,但也足以高度近似$(2)$式了。这样一来,判别器就可以定义为$f_w$。而对于公式中的Lipschitz连续限制,论文则是直接将判别器的所有参数$w_i$限制在某个范围$[-c,c]$内。因为我们其实无需关心具体的K是多少,它只是会使得梯度变大$K$倍,并不影响梯度的方向。
综上,判别器做的事就是优化判别器参数,来计算真实分布与生成分布之间的Wasserstein距离,也就是最大化$(4)$式。损失函数如下:
\begin{equation} \begin{aligned}L(w)= -\mathbb{E}_{x\sim P_r}[f_w(x)] +\mathbb{E}_{x\sim P_g}[f_w(x)] \end{aligned} \end{equation}
而生成器做的事则是优化生成器的参数,最小化真实分布与生成分布之间的Wasserstein距离,也就是最小化$(4)$式。忽略生成器参数的无关项,损失函数如下:
\begin{equation} \begin{aligned}L(\theta)= -\mathbb{E}_{x\sim P_g}[f_w(x)] \end{aligned} \end{equation}
生成器参数$\theta$控制生成分布$P_g$。
WGAN优化式写成最小最大的形式如下:
\begin{equation} \begin{aligned} \min\limits_{\theta:P_g}\max\limits_{w:|f_w|_L\le K}\mathbb{E}_{x\sim P_r}[f_w(x)] -\mathbb{E}_{x\sim P_g}[f_w(x)] \end{aligned} \end{equation}
论文中训练WGAN的算法如下:

总的来说,尽管上面写了一大通,WGAN对原始GAN做出的实际改进十分简洁,只有四点:
1、判别器输出层去掉sigmoid。
2、生成器和判别器的loss不取log
3、将判别器参数的绝对值截断在常数$c$以内。
4、不要用基于动量的优化算法,推荐RMSProp,SGD也行(这是实验得出的结论)。


