HMM——隐马尔可夫模型详解
隐马尔可夫模型(Hidden Markov Model, HMM)是可用于标注问题的模型,描述由隐藏的马尔可夫链随机生成观测序列的过程,属于生成模型。马尔可夫链不懂的可以把本科的《概率论与数理统计》找回来看一下,并不难,就是离散状态之间的转换。下面直接定义基本概念,为后面的算法做准备。
基本概念
变量定义
HMM各个时期会处于各种状态,设$Q$是所有可能状态的集合;每个状态可以产生各种观测,设$V$是所有可能观测的集合。$Q,V$的定义如下:
$Q=\{q_1,q_2,\dots, q_N\},\;\;V=\{v_1,v_2,\dots,v_M\}$
其中$N$是可能的状态数,$M$是可能的观测数。注意,这里的状态和观测不一定是数字,也可以是各种具体的对象。
然后定义$S$为长度为$T$的模型状态序列,定义$O$为对应的观测序列。
$S=(s_1,s_2,\dots,s_T),\;\;O=(o_1,o_2,\dots,o_T)$
这两个序列都是整数列表,其中每个整数索引对应的状态和观测。比如:$q_{s_2}$表示模型在时刻2时的状态,$v_{o_5}$表示模型在时刻5时的观测,而$s_2,o_5$并不代表那时模型的状态和观测本身(这里先说清楚,不然后面容易混淆)。
那么这些状态是如何初始化并相互转换,观测又是如何进行的呢?下面定义三个分布:
1、初始概率分布。时间开始时,各个状态出现的概率。定义为向量$\pi$:
$\begin{aligned}&\pi = [\pi_1,\pi_2,\dots,\pi_N]^T\\ &\pi_i=P(s_1=i),\;\;i = 1,2,\dots,N \end{aligned}$
2、状态转移分布。上一时刻到下一时刻不同状态之间转换的概率。定义为矩阵$A$:
$\begin{aligned} &A = [a_{ij}]_{N\times N}\\& a_{ij} = P(s_{t+1}=j|s_t=i)\end{aligned}$
3、观测概率分布。定义某个状态下各种观测出现的概率。定义为矩阵$B$:
$\begin{aligned} &B = [b_{ij}]_{N\times M}\\& b_{ij} = P(o_t=j|s_t=i) \end{aligned}$
隐马尔可夫模型由以上三个分布决定,因此可以用一个三元符号表示:
$\lambda = (A,B,\pi)$
HMM基本假设
从定义可知,HMM做了两个基本假设:
1、齐次马尔可夫性假设。任意时刻的状态只依赖于前一时刻的状态,与其它时刻的状态及观测无关:
$P(s_t|s_{t-1},o_{t-1},\dots,s_1,o_1) = P(s_t|s_{t-1})$
注意,以上条件概率中将除$s_{t-1}$以外的条件去掉,是因为$s_{t-1}$已知,并且没有之后时刻的状态或观测作为条件。如果$s_{t-1}$未知,则可以去掉$t$时刻之前的条件中,离$t$最近的$t^-$之前的状态和观测(包含$t^-$时刻的观测)。如:
$P(s_t|s_{t-2},o_{t-2},s_{t-3},s_{t-4}) = P(s_t|s_{t-2})$
另外,假如有之后时刻的状态,计算的概率就是后验概率了,那么之后时刻的状态作为条件来说也不能去掉。但是可以去掉$t$时刻之后的条件中,离$t$最近的$t^+$之后的状态和观测(包含$t^+$时刻的观测)如:
$\begin{gather}P(s_t|s_{t-2},s_{t-1},o_{t-1},o_{t+1},s_{t+2},o_{t+2},o_{t+3}) = P(s_t|s_{t-1},o_{t+1},s_{t+2})\label{}\end{gather}$
总之,就是近的状态已知,远的状态对于计算条件概率来说就没有意义了。
2、观测独立性假设。任意时刻的观测只依赖于此刻的状态,与其它无关:
$P(o_t|s_t,o_{t-1},\dots,s_1,o_1) = P(o_t|s_t)$
这个条件概率和上面也一样,也是近的状态已知,远处的状态作为条件就无意义。
以上两个假设和马尔可夫链的“链”相符,状态条件的已知就好像把链条对应结点的外侧链条砍断(靠近$s_t$的是内侧),我觉得把这种性质称作“就近原则”也不错(留意后面很多计算都用到)。下面是$(1)$式的示意图:

其中黄色结点表示已知条件,圈在虚线中的表示会影响$(1)$式概率值的状态与观测。
三个基本问题
弄懂HMM状态之间的转换规则后,现在提出HMM的三个基本问题:
1、概率计算。给定模型$\lambda$和观测序列$O$,计算在该模型下观测序列$O$出现的概率$P(O|\lambda)$ 。
2、学习。已知观测序列$O$,估计模型$\lambda$的参数,使得在该模型下观测到这个序列的概率$P(O|\lambda)$最大。
3、预测,或是解码。已知模型$\lambda$,给定观测序列$O$,求与之对应的状态序列$S$,使得概率$P(S|O,\lambda)$最大。
这三个基本问题分别阐述了HMM的基本推算方式和主要用途。下面依次介绍这三个基本问题的解法。
概率计算
对于给定的模型参数$\lambda =(A,B,\pi)$,计算观测序列$O= (o_1,o_2,\dots,o_T)$出现的概率,最简单的就是把所有可能的状态序列的概率都计算出来,然后选择最大的那个。但是这个方法计算复杂度是极大的,高达$O(TN^T)$阶,所以不可行。下面介绍两种计算可行的算法:前向和后向算法。
前向算法
定义到达时刻$t$,观测序列为$(o_1,o_2,\dots,o_t)$,且此时状态为$q_i$的概率
$\alpha_t(i) = P(o_1,o_2,\dots,o_t,s_t=i|\lambda)$
为前向概率。前向算法就是用$\alpha_t(i)$前向递推计算观测序列的概率。下面是算法的推算流程:
1、计算初值。即当$t=1$时所有状态的$\alpha$,一共$N$个:
$\begin{aligned}\alpha_1(i)=P(o_1,s_1=i|\lambda)=\pi_ib_{io_1},\;\;i=1,2,\dots,N\end{aligned}$
2、递推。对$t=2,3,\dots,T$,计算所有状态的$\alpha$,每个$t$同样都要计算$N$个:
$ \begin{aligned} &\alpha_t(i) \\ =& P(o_1,o_2,...,o_t,s_t=i|\lambda)\\ =& \sum\limits_{j=1}^NP(o_1,o_2,...,o_{t},s_{t-1}=j,s_t=i|\lambda) \\ =& \sum\limits_{j=1}^N P(o_t|o_1,o_2,...,o_{t-1},s_{t-1}=j,s_t=i,\lambda)P(o_1,o_2,...,o_{t-1},s_{t-1}=j,s_t=i|\lambda) \\ =& \sum\limits_{j=1}^N P(o_t|s_t=i,\lambda)P(o_1,o_2,...,o_{t-1},s_{t-1}=j|\lambda)P(s_t=i|o_1,o_2,...,o_{t-1},s_{t-1}=j,\lambda) \\ =& P(o_t|s_t=i,\lambda)\sum\limits_{j=1}^N P(o_1,o_2,...,o_{t-1},s_{t-1}=j|\lambda)P(s_t=i|s_{t-1}=j,\lambda) \\ =& b_{io_i}\sum\limits_{j=1}^N\alpha_{t-1}(j)a_{ji},\;\;i=1,2,...,N \end{aligned} $
3、计算最后的概率:
$ \begin{aligned} P(O|\lambda) =\sum\limits_{i=1}^NP(o_1,o_2,...,o_T,s_T=i|\lambda) =\sum\limits_{i=1}^N\alpha_T(i) \end{aligned} $
下面是书上的计算图,便于理解:
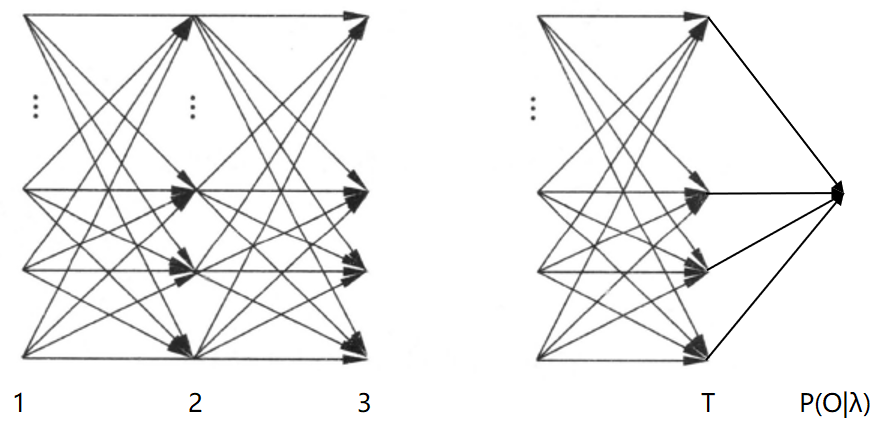
后向算法
定义在$t$时刻的状态为$q_i$的条件下,之后观测序列为$(o_{t+1},o_{t+2},\dots,o_T)$的条件概率
$\beta_t(i) = P(o_{t+1},o_{t+2},\dots,o_T|s_t=i,\lambda)$
为后向概率。与前向算法类似,后向算法是用$\beta_t(i)$后向推算概率。下面是递推流程:
1、定义初值:
$\begin{aligned}&\beta_T(i)=1,\;\;i=1,2,...,N\\\end{aligned}$
2、对$t=T-1,T-2,...,1$,计算:
$ \begin{aligned} &P(o_{t+1},...,o_T|s_t=i,\lambda)\\ =&\sum\limits_{j=1}^NP(o_{t+1},...,o_T,s_{t+1}=j|s_t=i,\lambda)\\ =&\sum\limits_{j=1}^NP(o_{t+1}|o_{t+2},...,o_T,s_{t+1}=j,s_t=i,\lambda)P(o_{t+2},...,o_T,s_{t+1}=j|s_t=i,\lambda)\\ =&\sum\limits_{j=1}^NP(o_{t+1}|s_{t+1}=j,\lambda)P(o_{t+2},...,o_T|,s_{t+1}=j,s_t=i,\lambda)P(s_{t+1}=j|s_t=i,\lambda)\\ =&\sum\limits_{j=1}^NP(o_{t+1}|s_{t+1}=j,\lambda)P(o_{t+2},...,o_T|,s_{t+1}=j,\lambda)P(s_{t+1}=j|s_t=i,\lambda)\\ =&\sum\limits_{j=1}^N a_{ij}b_{jo_{t+1}}\beta_{t+1}(j),\;\;i=1,2,...,N\\ \end{aligned} $
3、计算结果:
$ \begin{aligned} P(O|\lambda) = \sum\limits_{i=1}^N\pi_ib_{io_1}\beta_1(i) \end{aligned} $
利用前后向算法计算某些概率
我们可以用$\alpha$和$\beta$计算某些概率。
1、给定$\lambda$,计算以观测$O$为条件,$t$时刻状态为$q_i$的条件概率:
$ \begin{aligned} &P(s_t=i|O,\lambda)\\ =&\frac{ P(o_1,...,o_T,s_t=i|\lambda) }{P(O|\lambda)}\\ =&\frac{ P(o_1,...,o_t,s_t=i|\lambda)P(o_{t+1},...,o_T|o_1,...,o_t,s_t=i,\lambda) }{P(O|\lambda)}\\ =&\frac{ P(o_1,...,o_t,s_t=i|\lambda)P(o_{t+1},...,o_T| s_t=i,\lambda) }{\sum\limits_{j=1}^NP(o_1,...,o_T,s_t=j|\lambda)}\\ =&\frac{ \alpha_t(i)\beta_t(i) }{\sum\limits_{j=1}^N\alpha_t(j)\beta_t(j)}\\ \end{aligned} $
2、给定$\lambda$,计算以观测$O$为条件,$t$时刻状态为$q_i$,且$t+1$时刻状态为$q_j$的条件概率:
$\begin{aligned}&P(s_t=i,s_{t+1}=j|O,\lambda)\\=&\frac{\alpha_t(i)a_{ij}b_{jo_{t+1}}\beta_{t+1}(j)}{P(O|\lambda)}\\=&\frac{\alpha_t(i)a_{ij}b_{jo_{t+1}}\beta_{t+1}(j)}{\sum\limits_{k=1}^N\sum\limits_{l=1}^NP(s_t=k,s_{t+1}=l,O|\lambda)}\\=&\frac{\alpha_t(i)a_{ij}b_{jo_{t+1}}\beta_{t+1}(j)}{\sum\limits_{k=1}^N\sum\limits_{l=1}^N\alpha_t(k)a_{kl}b_{lo_{t+1}}\beta_{t+1}(l)}\\\end{aligned}$
具体推算过程和1类似,也用到了“链”的性质把多余的条件去掉。
3、给定$\lambda$,以观测$O$为条件,求某个状态或某两个连续状态出现的期望(就是出现次数的期望)。直接对所有时刻的以上条件概率进行求和即可,不再详写。
学习
如果给你观测序列和对应的状态序列,那么直接用各种转移出现的频率来估计$\lambda=(A,B,\pi)$即可,这很简单,就不讲了。而如果只给你观测序列,正如上面基本问题中定义的那样,就不能直接计算了,需要使用EM算法(点击链接)来迭代计算,就是所谓的Baum-Welch算法(实际上就是EM算法的应用)。
Q函数
因为只有观测序列,其未知的状态序列就可以看做隐变量。假设用于训练的观测序列集合为:
$\mathbb{O} = \{O_1,O_2,\dots,O_{|\mathbb{O}|}\}$
其中任意观测序列$O_i$的长度都为$T$。
然后假定隐变量状态序列的所有可能性集合为:
$\mathbb{S} = \{\left.S=(s_1,s_2,\dots,s_T)\right|s_t = 1,2,\dots,N,\;\;t = 1,2,\dots,T\}$
于是可以定义第k次迭代的$Q$函数:
$\displaystyle Q(\lambda,\lambda^k) = \sum\limits_{\mathbb{O}}\sum\limits_{\mathbb{S}}P(S|O,\lambda^k)\log P(S,O|\lambda)$
这里$Q$函数的定义与《统计学习方法》上定义的不同,为了更严谨,我把所有观测数据都算上了。
代入待优化参数,然后进行分解:
$ \begin{aligned} Q\left(\lambda,\lambda^k\right) &= \sum\limits_{\mathbb{O}}\sum\limits_{\mathbb{S}}P\left(S|O,\lambda^k\right) \log \left(\pi_{s_1}b_{s_1o_1}a_{s_1s_2}b_{s_2o_2}\dots a_{s_{T-1}s_T}b_{s_To_T}\right)\\ &= \sum\limits_{\mathbb{O}}\sum\limits_{\mathbb{S}}P\left(S|O,\lambda^k\right) \left(\log \pi_{s_1}+\sum\limits_{t = 1}^{T-1}\log a_{s_ts_{t+1}}+\sum\limits_{t = 1}^T\log b_{s_to_t}\right) \end{aligned} $
可以看到待优化式子分解为三个不同待优化变量的求和,因此可以将它们分开分别进行优化。
优化π
首先对$\pi$的优化式进行整理,将每个优化变量$\pi_i$的系数合并:
$ \begin{gather} \begin{aligned} & \sum\limits_{\mathbb{O}}\sum\limits_{\mathbb{S}}P\left(S|O,\lambda^k\right) \log \pi_{s_1}\\ =& \sum\limits_{\mathbb{O}}\sum\limits_{i=1}^N \sum\limits_{\{S|S\in \mathbb{S},s_1=i\}}P(S|O,\lambda^k) \log \pi_i\\ =& \sum\limits_{\mathbb{O}}\sum\limits_{i=1}^N\sum\limits_{1\le s_2,\dots,s_T \le N}P\left(s_1=i,s_2,s_3,\dots,s_T|O,\lambda^k\right) \log \pi_i\\ =& \sum\limits_{\mathbb{O}}\sum\limits_{i=1}^N P\left(s_1=i|O,\lambda^k\right) \log \pi_i\\ \end{aligned}\label{} \end{gather} $
上式第一个等号成立是因为$\sum\limits_{\mathbb{S}}$和$\sum\limits_{i=1}^N \sum\limits_{\{S|S\in \mathbb{S},s_1=i\}}$是等价的。
注意到等式约束$\sum\limits_{i=1}^N\pi_i=1$为仿射函数,并且上式为凸函数,因此这是一个带等式约束的凸优化(满足KKT条件(点击链接)即可)。写出拉格朗日函数:
$ \begin{aligned} L(\pi,\gamma) = \sum\limits_{\mathbb{O}}\sum\limits_{i=1}^N P\left(s_1=i|O,\lambda^k\right) \log \pi_i + \gamma\left(\sum\limits_{i=1}^N\pi_i-1\right) \end{aligned} $
对每个$\pi_i$求导并等于0、化简,再联立等式约束,得KKT条件:
$ \left\{ \begin{aligned} & \frac{\partial L}{\partial\pi_i}=\sum\limits_{\mathbb{O}}\frac{1}{\pi_i} P\left(s_1=i|O,\lambda^k\right) +\gamma=0,\;\;i=1,2,\dots,N\\ &\sum\limits_{i=1}^N\pi_i=1 \end{aligned} \right. $
将分母的$\pi_i$乘过去然后求和计算$\gamma$:
$\displaystyle\sum\limits_{\mathbb{O}} \sum\limits_{i=1}^N P\left(s_1=i|O,\lambda^k\right) +\sum\limits_{i=1}^N\gamma\pi_i=0$
$|\mathbb{O}| +\gamma=0$
$\gamma=-|\mathbb{O}| $
其中$|\mathbb{O}|$是用于训练的观测序列数。再计算$\pi_i$:
$ \begin{gather}\begin{aligned} & \pi_i = \frac{1}{|\mathbb{O}|}\sum\limits_{\mathbb{O}} P\left(s_1=i|O,\lambda^k\right) \end{aligned} \label{}\end{gather} $
优化a
$a$的优化式:
$ \begin{aligned} & \sum\limits_{\mathbb{O}}\sum\limits_{\mathbb{S}}P\left(S|O,\lambda^k\right)\sum\limits_{t = 1}^{T-1}\log a_{s_to_{t+1}}\\ \end{aligned} $
和$\pi_i$一样,也要先将每个$a_{ij}$的系数合并。为了容易理解,先对单个的$a_{s_ts_{t+1}}$进行整理:
$ \begin{aligned} & \sum\limits_{\mathbb{O}}\sum\limits_{\mathbb{S}}P\left(S|O,\lambda^k\right)\log a_{s_to_{t+1}}\\ =& \sum\limits_{\mathbb{O}}\sum\limits_{i=1}^N\sum\limits_{j=1}^N\sum\limits_{\{S|S\in\mathbb{S},s_t=i,s_{t+1}=j\}}P\left(S|O,\lambda^k\right)\log a_{ij}\\ =& \sum\limits_{\mathbb{O}}\sum\limits_{i=1}^N\sum\limits_{j=1}^NP\left(s_t=i,s_{t+1}=j|O,\lambda^k\right)\log a_{ij}\\ \end{aligned} $
再加上$t$的求和,得到整理后的$a$的优化式:
$ \begin{aligned} & \sum\limits_{\mathbb{O}}\sum\limits_{i=1}^N\sum\limits_{j=1}^N\sum\limits_{t=1}^{T-1}P\left(s_t=i,s_{t+1}=j|O,\lambda^k\right)\log a_{ij}\\ \end{aligned} $
类似于优化$\pi$,列出具有$N$个等式约束$\sum\limits_{j=1}^Na_{ij}=1$的拉格朗日函数:
$ \begin{aligned} L(a,\gamma) =\sum\limits_{\mathbb{O}}\sum\limits_{i=1}^N\sum\limits_{j=1}^N\sum\limits_{t=1}^{T-1}P\left(s_t=i,s_{t+1}=j|O,\lambda^k\right)\log a_{ij} +\sum\limits_{i=1}^N\gamma_i\left(\sum\limits_{j=1}^Na_{ij}-1\right) \end{aligned} $
列出KKT条件:
$ \left\{ \begin{aligned} &\frac{\partial L}{\partial a_{ij}} =\frac{1}{a_{ij}}\sum\limits_{\mathbb{O}}\sum\limits_{t=1}^{T-1}P\left(s_t=i,s_{t+1}=j|O,\lambda^k\right) +\gamma_i =0,\;\;i,j=1,2,\dots,N\\ &\sum\limits_{j=1}^Na_{ij}=1,\;\;i=1,2,\dots,N \end{aligned}\right. $
求和计算得$\gamma$:
$\displaystyle \gamma_i = -\sum\limits_{\mathbb{O}}\sum\limits_{t=1}^{T-1}P\left(s_t=i|O,\lambda^k\right) $
再算$a_{ij}$:
$ \begin{gather}\begin{aligned} a_{ij} =\frac{\sum\limits_{\mathbb{O}}\sum\limits_{t=1}^{T-1}P\left(s_t=i,s_{t+1}=j|O,\lambda^k\right)}{\sum\limits_{\mathbb{O}}\sum\limits_{t=1}^{T-1}P\left(s_t=i|O,\lambda^k\right)}\\ \end{aligned} \label{}\end{gather} $
优化b
同样先将每个$b_{ij}$的系数进行合并:
$ \begin{gather} \begin{aligned} &\sum\limits_{\mathbb{O}}\sum\limits_{\mathbb{S}}P\left(S|O,\lambda^k\right) \sum\limits_{t = 1}^T\log b_{s_to_t}\\ =&\sum\limits_{\mathbb{O}}\sum\limits_{\mathbb{S}}\sum\limits_{t = 1}^TP\left(S|O,\lambda^k\right) \log b_{s_to_t}\\ =&\sum\limits_{j=1}^M\sum\limits_{i=1}^N\sum\limits_{t = 1}^T \sum\limits_{\{O|O\in \mathbb{O},o_t=j\}} \sum\limits_{\{S|S\in \mathbb{S},s_t=i\}} P\left(S|O,\lambda^k\right) \log b_{ij}\\ =&\sum\limits_{j=1}^M\sum\limits_{i=1}^N\sum\limits_{t = 1}^T \sum\limits_{\{O|O\in \mathbb{O},o_t=j\}} P\left(s_t=i|O,\lambda^k\right) \log b_{ij}\\ \end{aligned} \label{} \end{gather} $
列出包含约束的拉格朗日函数:
$ \begin{gather} \begin{aligned} L(b,\gamma)=&\sum\limits_{j=1}^M\sum\limits_{i=1}^N\sum\limits_{t = 1}^T \sum\limits_{\{O|O\in \mathbb{O},o_t=j\}} P\left(s_t=i|O,\lambda^k\right) \log b_{ij} +\sum\limits_{i=1}^N\gamma_i\left(\sum\limits_{j=1}^Mb_{ij}-1\right) \\ \end{aligned}\label{} \end{gather} $
这里说明一下,$b$和$\pi,a$不同,$b_{ij}$是否为0是与训练数据集$\mathbb{O}$直接相关的。比如在$\mathbb{O}$没有出现观测$v_3$,那我们可以直接将所有$b_{i3}$估计为0,这是符合常理的。而在$(6)$式中,因为不存在$o_t=3$的$O$,所以$\log b_{i3}$也不存在,于是对$\log b_{i3}$求导也没法求,就不能参与优化了,直接估计为0即可。另外,$\pi,a$是与隐变量状态序列相关的,而隐变量我们是要考虑所有可能的情况的,所以所有$\pi_i,a_{ij}$都可以参与优化。
下面对非0的$b_{ij}$进行求导并令其为0,联立约束列出KKT条件:
$ \left\{ \begin{aligned} &\frac{\partial L}{\partial b_{ij}} =\frac{1}{b_{ij}}\sum\limits_{t = 1}^T \sum\limits_{\{O|O\in \mathbb{O},o_t=j\}} P\left(s_t=i|O,\lambda^k\right) + \gamma_i =0,\;\; i=1,2,\dots,N,\;\;j=1,2,\dots,M \\ &\sum\limits_{j=1}^Mb_{ij}= 1,\;\;i=1,2,\dots,N \end{aligned}\right. $
计算$\gamma$:
$ \displaystyle\sum\limits_{j = 1}^M \sum\limits_{t = 1}^T \sum\limits_{\{O|O\in \mathbb{O},o_t=j\}} P\left(s_t=i|O,\lambda^k\right) + \gamma_i = 0 $
$ \displaystyle \gamma_i = -\sum\limits_{\mathbb{O}} \sum\limits_{t = 1}^T P\left(s_t=i|O,\lambda^k\right) $
计算优化$b$:
$ \displaystyle b_{ij}= \frac{\sum\limits_{t = 1}^T \sum\limits_{\{O|O\in \mathbb{O},o_t=j\}} P\left(s_t=i|O,\lambda^k\right) } {\sum\limits_{\mathbb{O}} \sum\limits_{t = 1}^T P\left(s_t=i|O,\lambda^k\right)} $
算上训练数据$\mathbb{O}$中不包含某观测$v_j$,使得$b_{ij}=0$的情况(其实上式已经包含了,但是我不确定是看做0还是看做不存在,为了严谨还是显式写出来好了):
\begin{gather} b_{ij}=\left\{ \begin{aligned} &\frac{\sum\limits_{t = 1}^T \sum\limits_{\{O|O\in \mathbb{O},o_t=j\}} P\left(s_t=i|O,\lambda^k\right) } {\sum\limits_{\mathbb{O}} \sum\limits_{t = 1}^T P\left(s_t=i|O,\lambda^k\right)}, &\exists O\in \mathbb{O}, j\in O \\ &0,& \forall O\in \mathbb{O}, j\notin O \end{aligned}\right. \label{}\end{gather}
迭代
综上,使用EM算法迭代计算HMM参数的步骤如下:
0、初始化$\lambda^0 = (\pi^0,A^0,B^0)$,各取为符合约束的随机值。
1、第$k$次迭代,在$\lambda^{k-1}$的基础上分别使用$(3),(4),(7)$式对$\pi,a,b$进行优化,得到$\lambda^k$。
2、判断终止条件,满足即完成迭代,否则回到第一步执行下一次迭代。
预测
预测问题最直观的方式,就是直接选择每个时刻最有可能出现的状态$s_t^*$,从而预测整个状态序列,即:
$ \begin{aligned} &s_t^* = \arg\max\limits_{1\le i \le N} \frac{\alpha_t(i)\beta_t(i)}{\sum\limits_{j=1}^N\alpha_t(j)\beta_t(j)},\;\;t=1,2,...,T\\ &S = (s_1^*,s_2^*,...,s_T^*) \end{aligned} $
但这并不是整体最优的,而且它并不能剔除因为状态转移概率为0而不可能出现的状态序列。为了整体最优并且符合状态转移概率矩阵,我们通常使用维特比算法来预测状态序列。
维特比算法
维特比算法实际上就是动态规划,在递推的过程中保持步步最优,从而最终达到全局最优的目的。
定义在$t$时刻以内,且$t$时刻状态为$q_i$的所有状态序列的出现概率的最大值为:
$ \begin{gather} \begin{aligned} \delta_t(i) = \max_{s_1,...,s_{t-1}}P(s_t=i,s_{t-1},...,s_1,o_t,...,o_1|\lambda),\;\;i=1,2,...,N \end{aligned} \label{}\end{gather} $
由定义可以获得$\delta$的递推公式:
$ \begin{aligned} &\delta_{t+1}(i) \\ =& \max_{s_1,...,s_t}P(s_{t+1}=i,s_t,...,s_1,o_{t+1},...,o_1|\lambda)\\ =& \max_{s_t}\max_{s_1,...,s_{t-1}}P(s_{t+1}=i,s_t,...,s_1,o_{t+1},...,o_1|\lambda)\\ =& \max_{1\le j\le N}\max_{s_1,...,s_{t-1}}P(s_{t+1}=i,s_t=j,s_{t-1},...,s_1,o_{t+1},...,o_1|\lambda)\\ =& \max_{1\le j\le N}\max_{s_1,...,s_{t-1}}\left[P(o_{t+1}|s_{t+1}=i,\lambda)P(s_{t+1}=i,s_t=j,s_{t-1},...,s_1,o_t,...,o_1|\lambda)\right]\\ =& P(o_{t+1}|s_{t+1}=i,\lambda)\max_{1\le j\le N}\max_{s_1,...,s_{t-1}}\left[P(s_{t+1}=i|s_t=j,\lambda)P(s_t=j,s_{t-1},...,s_1,o_t,...,o_1|\lambda)\right]\\ =& P(o_{t+1}|s_{t+1}=i,\lambda)\max_{1\le j\le N}\left[P(s_{t+1}=i|s_t=j,\lambda)\max_{s_1,...,s_{t-1}}P(s_t=j,s_{t-1},...,s_1,o_t,...,o_1|\lambda)\right]\\ =& b_{io_{t+1}}\max_{1\le j\le N}a_{ji}\delta_t(j) \end{aligned} $
以上算的是概率,并没有获取每个时刻下的状态编号。所以再定义:
$ \begin{gather} \begin{aligned} \Psi_t(i) = \arg\max_{1\le j\le N} \left[\delta_{t-1}(j)a_{ji}\right],\;\;i=1,2,...,N \end{aligned} \label{}\end{gather} $
用来回溯获取状态序列。
维特比算法用已知观测序列预测状态序列过程如下:
1、初始化。直接计算$\delta_1(i)$。
2、对$t=2,3,...,T$,使用递推公式计算$\delta_t(i)$,使用$(9)$式计算$\Psi_t(i)$。
3、使用$\Psi_t(i)$回溯,获取最大概率状态序列。
参考资料
李航《统计学习方法》


