深度学习优化算法总结与实验
深度学习优化算法最耳熟能详的就是GD(Gradient Descend)梯度下降,然后又有一个所谓的SGD(Stochastic Gradient Descend)随机梯度下降,其实还是梯度下降,只不过每次更新梯度不用整个训练集而是训练集中的随机样本。梯度下降的好处就是用到了当前迭代的一些性质,以至于总能较快找到驻点。而像遗传算法等智能优化算法,则是基于巨大的计算资源上的。它们并不使用函数特性,通常需要“种群”几乎遍布整个参数空间才能进行有效的优化,更像是一种暴力搜索。而因为神经网络参数量太大,几百万维的参数量不可能让种群达到“密布”(即使每个维度两个“个体”,种群规模也是2的百万次幂),所以神经网络优化通常都用基于梯度下降的算法。
现在,神经网络优化常用的都是梯度下降算法的变体,下面介绍Momentum, RMSProp, Adam这三种最常用的。它们都对梯度下降的某些不足做出了改进。
Momentum
Momentum是动量的意思。它对每次迭代进行平滑处理,以至于不会像GD一样,当梯度很大时一下子跳地太远,在梯度较小时又跳得太少。定义很简单,就比GD多了一步:
$V_t = \beta V_{t-1} + (1-\beta) \nabla \theta_t$
$\theta_{t+1} = \theta_t - \eta V_t$
其中$\theta_t$表示第$t$次迭代的参数张量,$\nabla \theta_t$表示关于它的梯度。$\eta$是模型学习率。$\beta$是平滑因子,也就是积累梯度的权重,越大则之前的梯度对当前影响越大,越小则此次迭代的梯度对当前影响越大,而等于0时Momentum就退化成GD了。$V_{t-1}$表示第$t$步迭代以前累积的梯度动量。
相较GD,加上平滑的概念以后,Momentum会更加注重优化的全局性,这是因为它每次迭代都取决于之前所有梯度的加权和。拿跑步来举例,GD的每一步都是当前地面坡度最陡的方向,而Momentum则是添加了惯性,每一步都将跑步速度向坡度最陡的方向调整。
RMSProp
RMSProp改进了GD的摆动幅度过大的问题,从而加快收敛速度。迭代式如下:
$\begin{gather}S_t = \beta S_{t-1} + (1-\beta)( \nabla \theta_t)^2 \label{}\end{gather}$
$\begin{gather}\displaystyle \theta_{t+1} = \theta_t - \eta \frac{\nabla \theta_t}{\sqrt{S_t}+\varepsilon}\label{}\end{gather}$
$(1)$式中的$( \nabla \theta_t)^2$和$(2)$式中的分式分别表示按元素进行的平方操作和除法操作。$(2)$式中的$\varepsilon$是为了防止除数为0而设置的较小数,它与张量$\sqrt{S_t}$执行的是按元素进行的加法。
按迭代式可以看出,RMSProp对梯度的方向进行了较弱的规范化,让梯度的每一个元素向单位值1或-1靠近,这样一来,优化时的摆动幅度就会减小一些。而又为了不至于靠得太近而直接变成全1和-1,用于规范化的是之前梯度平方的累积量而不是直接用当前梯度的平方。因此,如果$\beta=0$,那就是用当前梯度的平方来规范化,每次更新方向的每个元素值就都是1和-1了。下面来分析各种情况。
以下是分别用GD、Momentum、RMSProp对二元函数$z = x^2+10y^2$进行优化的例子,并且将numpy与pytorch方式都实现了一遍加以比较。初始点位于$(250,-150)$和$(-250,150)$,学习率分别为$0.02,0.02,20$,Momentum和RMSProp的$\beta$都为0.9。以函数值小于1为迭代结束的判断条件。图例中显示了迭代次数,如下:
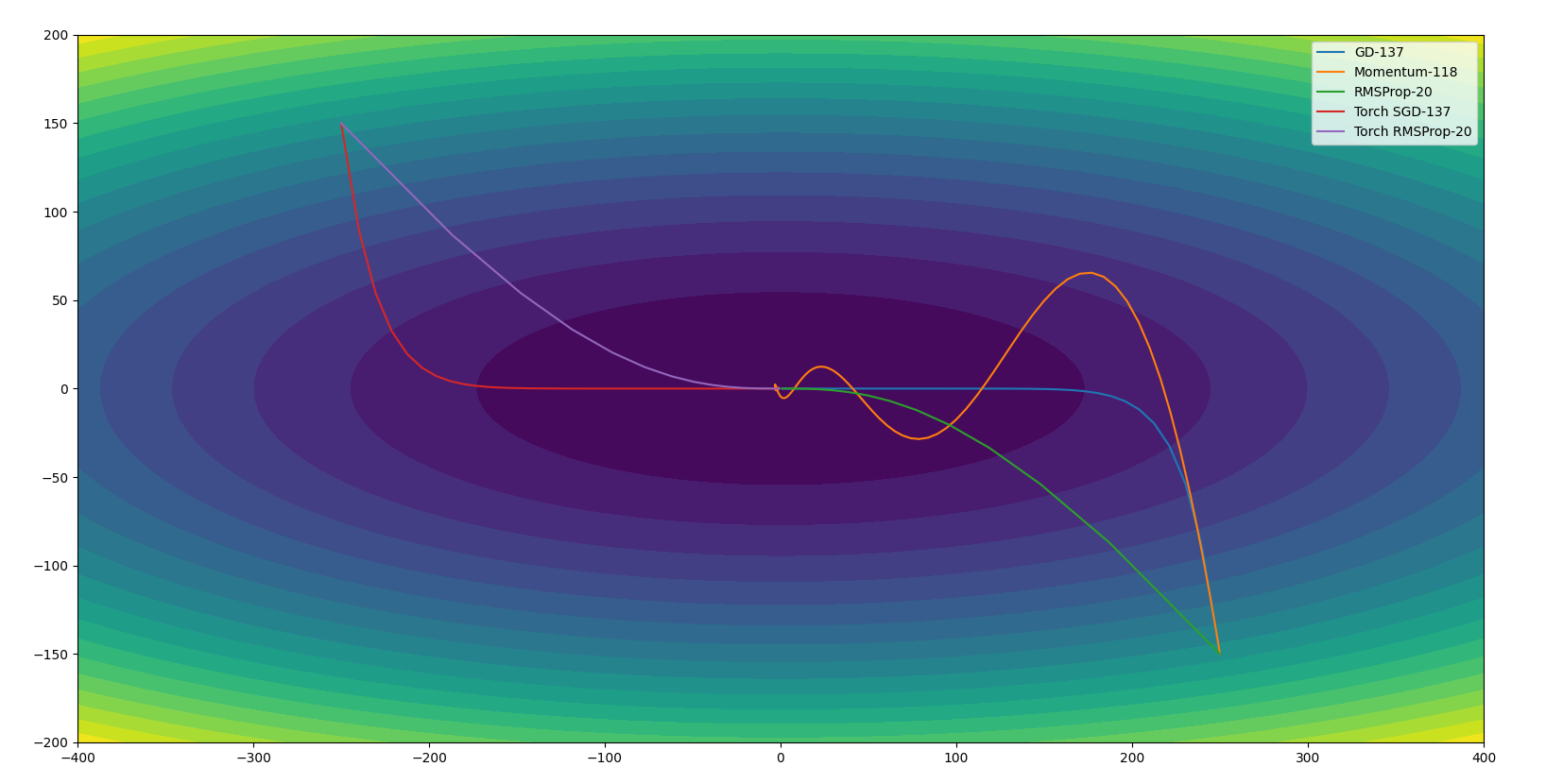
可以看出RMSProp少走了很多弯路,路线更平缓。Momentum虽然比GD多走很多弯路,但是迭代的次数还是有所下降的。
Adam
以上介绍的两个优化算法在不同的起始位置似乎各有优缺点,而Adam就是将Momentum和RMSProp的优势结合起来的算法。下面是迭代式:
$\begin{gather}V_t =\beta_1 V_{t-1} + (1-\beta_1) \nabla \theta_t\label{}\end{gather}$
$\begin{gather}S_t =\beta_2 S_{t-1} + (1-\beta_2)\nabla \theta_t^2 \label{}\end{gather}$
$\begin{gather}\hat{V_t} =\frac{V_t}{1-\beta_1^t}\label{}\end{gather}$
$\begin{gather}\hat{S_t} =\frac{S_t}{1-\beta_2^t} \label{}\end{gather}$
$\begin{gather}\theta_{t+1} = \theta_t - \eta \frac{\hat{V_t}}{\sqrt{\hat{S_t}}+\varepsilon} \label{}\end{gather}$
Adam实际上就是前面两个算法的简单结合,它还除以了$1-\beta^t$($\beta^t$表示$\beta$的$t$次方),这是为了让开始的几次更新不至于太小(因为乘了$1-\beta$)。随着迭代往后,$1-\beta^t$接近于1。
依旧是对二元函数$z = x^2+10y^2$进行优化,初始点位于$(250,-150)$和$(-250,150)$,学习率分别为为$0.02,0.02,20,20$。Momentum和RMSProp的$\beta=0.9$,Adam的$\beta_1=0.9$,$\beta_2=0.999$。如下:
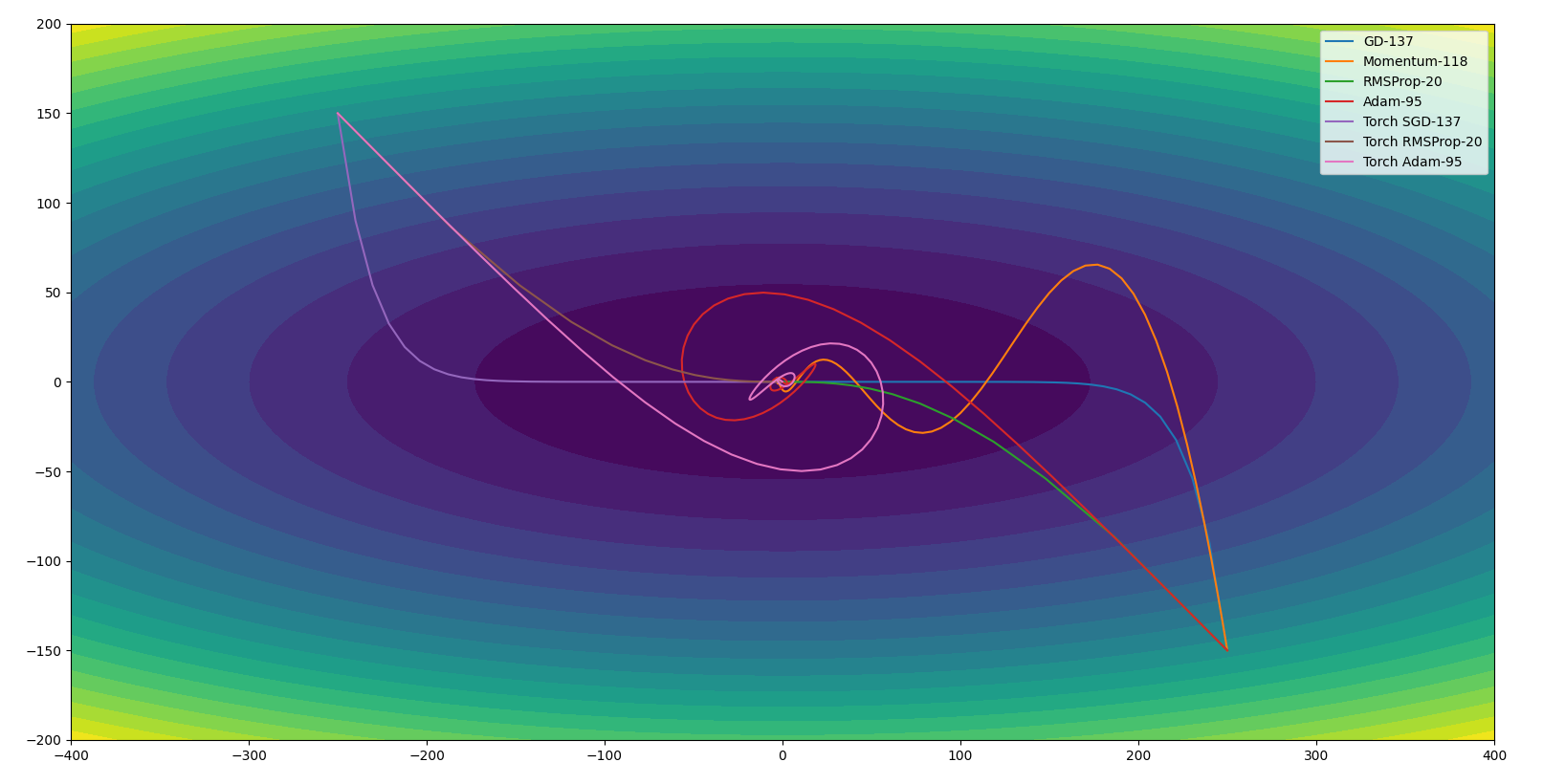
Adam绕得厉害,迭代次数也并不是最少的。把$\beta1$改成0.5后,Adam的迭代次数变为了30:
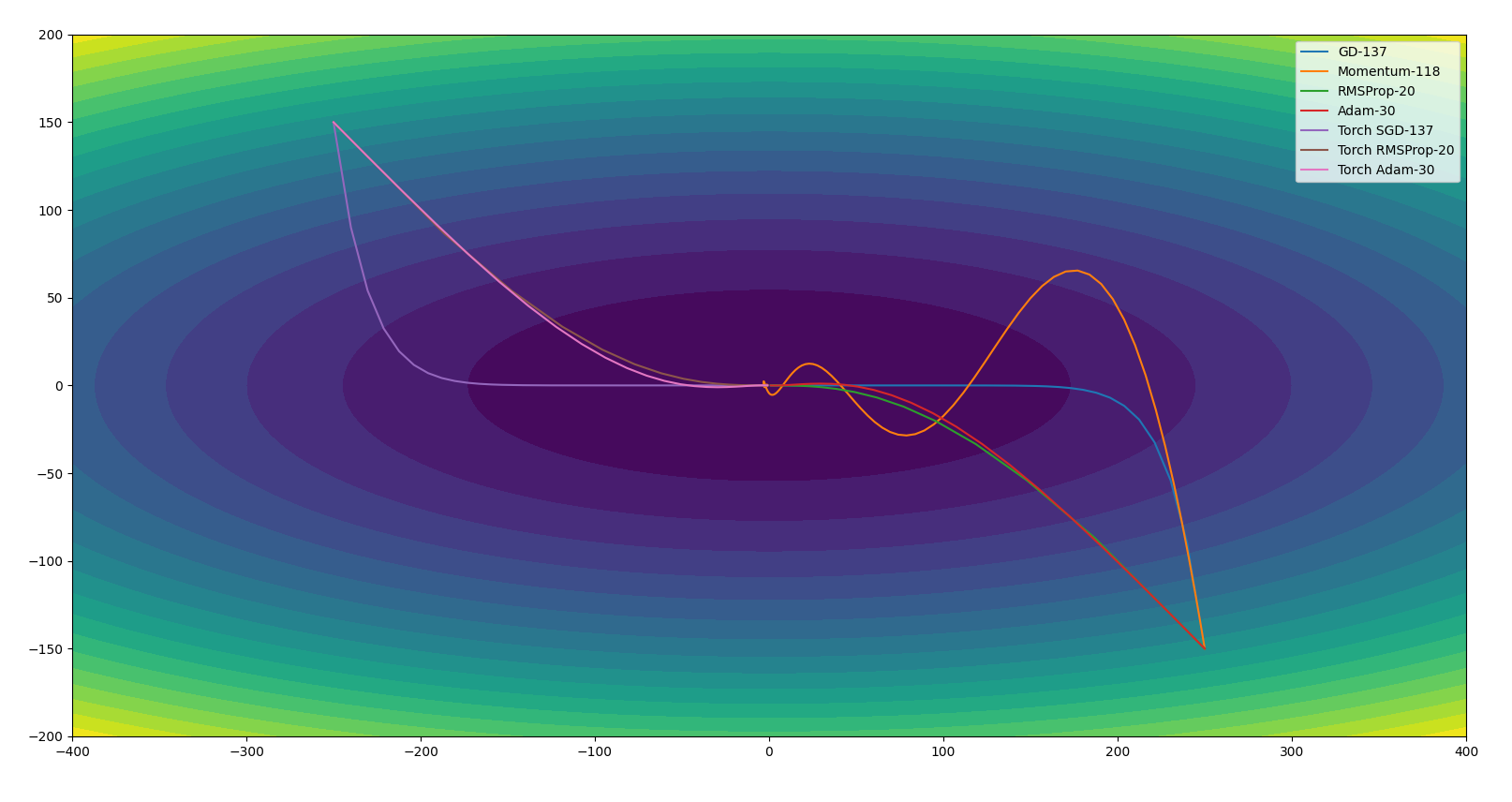
$\beta1$越小,Adam越退化为RMSProp。以上说明不同情况下Adam的参数设置会直接影响迭代效率。
总的来说,Adam就是加上动量的同时,又使用了规范化,让每次迭代能用上之前的梯度,并且更新步伐的每个元素稍微靠近1和-1一些。而这样有什么好处,只能实践出真知。
总结
这些基于梯度下降的优化算法都大同小异,它们在不同情况下发挥时好时坏,有的改良算法在某些情况下效果可能比原始的GD还差。所以选择优化算法还是要视情况而定,我们应该选择对高概率情况优化效果好的算法。另外,以上使用迭代次数来比较算法的优劣性并不严谨,因为不同算法每次迭代的计算量都不同。像Adam的计算量差不多是Momentum和RMSProp的两倍,如果要严谨,还是得用计算时间作比较。当然,相较于原始SGD,Adam等带动量的优化算法的优势并不只在于迭代消耗上,它们也为迭代跳出局部最优提供了帮助。所以,仅仅分析时间也并不全面,应该把跳出局部最优等能力也考虑在内。
代码
完整比较代码:
1 import numpy as np 2 import matplotlib.pyplot as plt 3 import torch 4 from torch.optim import RMSprop, Adam, SGD 5 6 def func(x, y): 7 return x ** 2 + 10 * y ** 2 8 def grad(x, y): 9 return np.array([2 * x, 20 * y]) 10 def paint(histories:dict): 11 x, y = np.linspace(-400,400,1000), np.linspace(-200,200,1000) 12 X, Y = np.meshgrid(x, y) 13 Z = func(X, Y) 14 plt.contourf(X,Y,Z,levels=20) 15 16 for his in histories: 17 plt.plot(histories[his][:,0],histories[his][:,1], label = his + '-' + str(histories[his].shape[0])) 18 19 plt.legend() 20 plt.show() 21 def optimization(point, opt, if_torch = False): 22 his = [] 23 if not if_torch: 24 t = 0 25 while(True): 26 his.append(point) 27 z = func(point[0], point[1]) 28 if z < 1: 29 print(z) 30 break 31 t+=1 32 point = point - opt.step(point, t) 33 else: 34 while(True): 35 his.append(np.array(point.detach())) 36 z = func(point[0], point[1]) 37 if z < 1: 38 print(z) 39 break 40 opt.zero_grad() 41 z.backward() 42 opt.step() 43 his = np.array(his) 44 return his 45 46 class update_SGD(): 47 def __init__(self, lr = 0.02): 48 self.lr = lr 49 def step(self, point, *arg): 50 return grad(point[0], point[1]) * self.lr 51 class update_Momentum(): 52 def __init__(self, lr = 0.02, beta = 0.9): 53 self.lr = lr 54 self.v = np.array([0,0]) 55 self.beta = beta 56 def step(self, point, *arg): 57 g = grad(point[0], point[1]) 58 self.v = self.beta * self.v + (1 - self.beta) * g 59 return self.v * self.lr 60 class update_RMSProp(): 61 def __init__(self, lr = 0.02, beta = 0.9): 62 self.lr = lr 63 self.s = np.array([0,0]) 64 self.beta = beta 65 def step(self, point, *arg): 66 g = grad(point[0], point[1]) 67 self.s = self.beta * self.s + (1 - self.beta) * (g ** 2) 68 return self.lr * g / (self.s ** 0.5) #* np.sum(self.s)**0.5 69 class update_Adam(): 70 def __init__(self, lr = 0.02, beta1 = 0.9, beta2=0.999): 71 self.lr = lr 72 self.v = np.array([0,0]) 73 self.s = np.array([0,0]) 74 self.beta1 = beta1 75 self.beta2 = beta2 76 def step(self, point, t:int): 77 g = grad(point[0], point[1]) 78 self.v = self.beta1 * self.v + (1 - self.beta1) * g 79 self.s = self.beta2 * self.s + (1 - self.beta2) * (g ** 2) 80 v_ = self.v/(1 - self.beta1 ** t) 81 s_ = self.s/(1 - self.beta2 ** t) 82 return v_/(s_**0.5) * self.lr #* np.sum(self.s)**0.5 83 start_point = np.array([250., -150]) 84 t_start_point = -start_point 85 histories = {} 86 87 opt = update_SGD(0.02) 88 his = optimization(start_point[:], opt) 89 histories["GD"] = his 90 91 opt = update_Momentum(0.02, 0.9) 92 his = optimization(start_point[:], opt) 93 histories["Momentum"] = his 94 95 opt = update_RMSProp(20, 0.9) 96 his = optimization(start_point[:], opt) 97 histories["RMSProp"] = his 98 99 opt = update_Adam(20, 0.5, 0.999) 100 his = optimization(start_point[:], opt) 101 histories["Adam"] = his 102 103 104 point = torch.tensor(t_start_point, requires_grad=True) 105 opt = SGD([point], 0.02) 106 his = optimization(point, opt, True) 107 histories["Torch SGD"] = his 108 109 point = torch.tensor(t_start_point, requires_grad=True) 110 opt = RMSprop([point], 20, 0.9) 111 his = optimization(point, opt, True) 112 histories["Torch RMSProp"] = his 113 114 point = torch.tensor(t_start_point, requires_grad=True) 115 opt = Adam([point], 20, (0.5, 0.999)) 116 his = optimization(point, opt, True) 117 histories["Torch Adam"] = his 118 119 paint(histories)


