SVM——支持向量机,人脸识别实验
最基本的SVM(Support Vector Machine)旨在使用一个超平面,分离线性可分的二类样本,其中正反两类分别在超平面的一侧。SVM算法则是要找出一个最优的超平面。
下面从简单到复杂介绍三种SVM形式,然后介绍一种快速优化SVM的算法,最后用SVM实现人脸识别。
线性可分SVM
优化函数定义
给定一个特征空间线性可分的数据集:
$T = \{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\}$
特征分布类似下图:
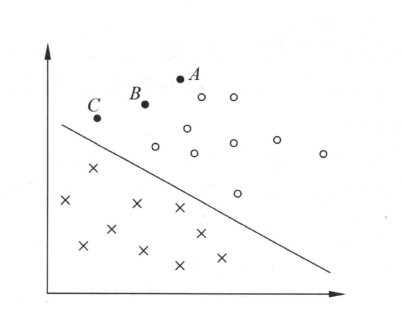
如上图,当特征空间为二维时,超平面就是比二维空间低一维度的直线。任意维超平面定义如下(其中$x$是$n$维特征向量,$w,b$是超平面系数):
$wx+b = 0$
对于正例应有$wx_i+b > 0$,反例应有$wx_i+b < 0$,也就是说,如果分类正确,应有:
$y_i(wx_i+b)> 0$
从直观上看,最优超平面,应该在将所有样本都正确分类的基础上,最大化超平面与离超平面最近的样本点的距离。点到面的距离公式中学学过
$\displaystyle \frac{|wx+b|}{|| w ||}$
综上,优化的问题用数学方式表达:
$\displaystyle\max\limits_{w,b}\min\limits_{i\in \{1,2,...,N\}}(\frac{y_i(wx_i+b)}{||w||})$
或者
$\begin{align*} &\max\limits_{w,b}\;\gamma \\ &\;\text{s.t.}\;\;\;y_i(\frac{w}{||w||}x_i+\frac{b}{||w||})\ge \gamma,\;\;i=1,2,...,N \end{align*}$
其中$\gamma$为最小距离。令$ \hat{\gamma}=\gamma||w|| $,即所谓“函数距离”,上式可变为:
$\begin{align*} &\max\limits_{w,b}\;\frac{\hat{\gamma}}{||w||} \\ &\;\text{s.t.}\;\;\;y_i(wx_i+{b})\ge \hat{\gamma },\;\;i=1,2,...,N\end{align*}$
$\hat{\gamma}$没有被$||w||$规范化,因此大小与$||w||$有关。而$w,b$等比例变化时,超平面并不会变。因此,可以固定$||w||=1$,最大化$\hat{\gamma}$,即:
$\begin{align*} &\max\limits_{w,b}\;\hat{\gamma}\\ &\;\text{s.t.}\;\;\;y_i(wx_i+{b})\ge \hat{\gamma },\;\;i=1,2,...,N;\\ &\;\;\;\;\;\;\;\;\; ||w||=1 \end{align*}$
或者固定$\hat{\gamma}=1$,最小化$||w||$,也就是:
$\begin{align*} &\min\limits_{w,b}\;\frac{1}{2}||w||^2 \\ &\;\text{s.t.}\;\;\;y_i(wx_i+{b})\ge 1,\;\;i=1,2,...,N\end{align*}$
通常是最小化$||w||$。这是一个凸二次规划问题,即待优化的函数$\frac{1}{2}||w||^2$是二次函数,不等式约束条件$1-y_i(wx_i+{b})\le 0$为可微凸函数(这是仿射函数,自然是凸函数)。
对偶算法
上述带约束优化满足原始问题最优值与对偶问题最优值取等的条件,因此可以使用拉格朗日对偶性(点击链接)将原始优化问题转换为其对偶问题求解。原始问题的拉格朗日函数为:
$\displaystyle \begin{gather}L(w,b,\alpha) = \frac{1}{2}||w||^2- \sum\limits_{i=1}^{N}\alpha_iy_i(wx_i+b)+\sum\limits_{i=1}^{N}\alpha_i,\,\,\alpha\ge 0 \label{}\end{gather}$
因此原始问题为:
$\displaystyle \begin{gather} \min\limits_{w,b}\max\limits_{\alpha\ge 0 }L(w,b,\alpha) \label{}\end{gather}$
则对偶问题为:
$\displaystyle \begin{gather}\max\limits_{\alpha\ge 0 } \min\limits_{w,b}L(w,b,\alpha) \label{}\end{gather}$
由KKT条件1式令梯度为0,计算对偶问题内部的$\min$函数
$\begin{aligned} &\nabla_wL(w,b,\alpha) = w-\sum\limits_{i=1}^{N}\alpha_iy_ix_i=0 \\ &\nabla_bL(w,b,\alpha) = -\sum\limits_{i=1}^{N}\alpha_iy_i=0 \\ \end{aligned}$
得
$\begin{gather} &w = \sum\limits_{i=1}^{N}\alpha_iy_ix_i \\ &\sum\limits_{i=1}^{N}\alpha_iy_i=0 \label{}\end{gather}$
代入$(3)$式,经过计算,对偶问题变为:
$\begin{gather} \begin{array}{lcl} \min\limits_{\alpha}\displaystyle\frac{1}{2}\sum\limits_{i=1}^{N}\sum\limits_{j=1}^{N}\alpha_i\alpha_jy_iy_j(x_ix_j)-\sum\limits_{i=1}^{N}\alpha_i \\ \begin{aligned} \text{s.t.}\;&\sum\limits_{i=1}^{N}\alpha_iy_i=0\\ &\alpha_i\ge 0,i = 1,2,...,N \end{aligned} \end{array} \end{gather}$
这样,只需先优化对偶问题,计算出最优的$\alpha^*$,再代入$(4)$式即可算出最优$w^*$。对于$b$,因为至少有一个$\alpha_j^*>0$(如果全都为0,由$(4)$式有$w=0$,不符合约束),对应KKT条件2式
$\alpha_i(y_i(wx_i+b)-1)=0$
于是有
$y_j(w^*x_j+b^*)-1=0$
实际上这个$x_j$就是与超平面最近的的样本,也就是所谓的支持向量。另外也说明了这个优化问题的解一定在不等式约束的边界上,而不在其内部。于是,提取$b^*$并将$(4)$式代入,得:
$\begin{gather}\displaystyle b^* = y_j-\sum\limits_{i=1}^{N}\alpha_i^*y_i(x_ix_j)\end{gather}$
综上,计算最优$w^*,b^*$的操作就是:先$(6)$式算出$\alpha^*$,再代入$(4),(7)$式算出$w^*,b^*$。
但是$(6)$实际上并不好算,当样本量一大,$\alpha$需要分类讨论的情况数以指数级上升(即每个$\alpha$是否为0),后面介绍开销小的算法。
线性SVM
参数计算
有时样本会有特异点,不能保证每个样本都满足不等式约束。因此修改上面的“硬间隔最大化”为“软间隔最大化”,则线性可分SVM变为线性SVM。即添加一个松弛变量$\xi$,允许原来的不等式约束不一定严格满足,当然在优化函数中也要把这一损失加上,乘上惩罚参数$C$。得到如下最优化问题:
$\begin{gather} \begin{array}{lcl} \min\limits_{w,b,\xi}\;\displaystyle\frac{1}{2}||w||^2+C\sum\limits_{i=1}^{N}\xi_i \\ \begin{aligned} \text{s.t.}\;\;\;&y_i(wx_i+{b})\ge 1-\xi_i,\;\;i=1,2,...,N\\ &\xi_i\ge 0,\;\;i=1,2,...,N\\ \end{aligned} \end{array}\end{gather}$
显然待优化函数与不等式约束都是凸函数(仿射函数也是凸函数)。因此同样符合KKT条件,可以对偶化计算。拉格朗日函数为:
$ \begin{aligned} \displaystyle L(w,b,\xi,\alpha,\mu) =& \frac{1}{2}||w||^2+C\sum\limits_{i=1}^{N}\xi_i-\sum\limits_{i=1}^{N}\alpha_i(y_i(wx_i+b)-1+\xi_i)-\sum\limits_{i=1}^{N}\mu_i\xi_i,\\ &\text{where}\;\;\alpha_i\ge 0,\mu_i\ge 0 \end{aligned} $
则原始问题变为:
$ \min\limits_{w,b,\xi}\max \limits_{\alpha\ge 0 ,\mu \ge 0}L(w,b,\xi,\alpha,\mu) $
其对偶问题为:
$\begin{gather} \max \limits_{\alpha\ge 0 ,\mu \ge 0}\min\limits_{w,b,\xi}L(w,b,\xi,\alpha,\mu) \end{gather}$
由KKT条件1式令梯度为0,计算对偶问题内部$\min$函数,得:
\begin{align} &\nabla_wL(w,b,\xi,\alpha,\mu) = w-\sum\limits_{i=1}^{N}\alpha_iy_ix_i=0 \\ &\nabla_bL(w,b,\xi,\alpha,\mu) = -\sum\limits_{i=1}^{N}\alpha_iy_i=0 \notag\\ &\nabla_{\xi_i}L(w,b,\xi,\alpha,\mu) = C-\alpha_i-\mu_i=0 \notag \end{align}
代入$(9)$式,对偶问题变为:
\begin{gather} \begin{array}{lcl} \min\limits_{\alpha}\displaystyle\frac{1}{2}\sum\limits_{i=1}^{N}\sum\limits_{j=1}^{N}\alpha_i\alpha_jy_iy_j(x_ix_j)-\sum\limits_{i=1}^{N}\alpha_i \\ \begin{aligned} \text{s.t.}\;&\sum\limits_{i=1}^{N}\alpha_iy_i=0\\ &0\le\alpha_i\le C,\;\;i = 1,2,...,N \end{aligned} \end{array} \end{gather}
其中$\alpha_i\le C$是由于$C-\alpha_i=\mu_i\ge0 $。类似地,接下来的操作就是:
1、算出$(11)$式的最优$\alpha^*$。
2、$\alpha^*$代入$(10)$式计算$w^*$。
3、找出满足$\alpha_j^*$满足$0<\alpha_j^*<C$。
此时$\mu_j^* = C-\alpha_j^*>0$,由KKT条件2式,有$\mu_j^*\xi_j^*=0$,因此$\xi_j^*=0$。
同样地,由KKT2式,有$\alpha_j^*(y_j(w^*x_j+b^*)-1+\xi_j^*)=0$,因$\alpha_j^*>0$,于是有:
$\displaystyle b^* = y_j-\sum\limits_{i=1}^{N}\alpha_i^*y_i(x_ix_j)$
支持向量
在线性SVM中,因为有松弛变量$\xi$,不等式约束取等时样本不一定在其类别的边界上。上面只讨论了使用小于$C$的$\alpha_j^*$,下面做个总结:
1、若$\alpha_i^* = 0$ ,则$\xi_i = 0$ ,分类正确,$x_i$在分离间隔边界的外侧;
2、若$0<\alpha_i^* < C$ ,则$\xi_i = 0$ ,分类正确,支持向量$x_i$恰好落在间隔边界上;
3、若$\alpha_i^* = C,0<\xi_i<1$ ,则分类正确,$x_i$在间隔边界与分离超平面之间;
4、若$\alpha_i^* = C,\xi_i=1$,则分类错误,$x_i$在分离超平面上;
5、若$\alpha_i^* = C,\xi_i>1$,则分类错误,$x_i$位于分离超平面误分一侧。
其中2~5都是支持向量。
合页损失函数
线性SVM还有另一种等价的优化目标函数:
$\begin{gather}\displaystyle \min\limits_{w,b}\sum\limits_{i=1}^{N}\left[1-y_i(wx_i+b)\right]_++\lambda||w||^2\end{gather}$
其中
$[z]_+= \left\{ \begin{aligned} &z,\;\;z>0 \\ &0,\;\;z\le0 \end{aligned} \right.$
感觉可以直接梯度下降。
等价性证明
令$(12)$中
$\left[1-y_i(wx_i+b)\right]_+=\xi_i$
则
1、有$\xi_i\ge 0$(一个不等式约束成立);
2、当$1-y_i(wx_i+b)>0$时,可得$y_i(wx_i+b)=1-\xi_i$;
3、当$1-y_i(wx_i+b)\le0$时,$\xi_i=0$,有$y_i(wx_i+b)\ge1-\xi_i$。
综合2、3,不论$1-y_i(wx_i+b)$如何取值,总有$y_i(wx_i+b)\ge1-\xi_i$(另一个不等式约束成立)。
于是$(12)$可写成:
\begin{array}{lcl} \min\limits_{w,b,\xi}\displaystyle\sum\limits_{i=1}^{N}\xi_i+\lambda||w||^2\\ \begin{aligned} \text{s.t.}\;\;\;&y_i(wx_i+{b})\ge 1-\xi_i,\;\;i=1,2,...,N\\ &\xi_i\ge 0,\;\;i=1,2,...,N\\ \end{aligned} \end{array}
然后优化项常系数权重改一下就和$(8)$一模一样了。
非线性SVM
对于特征分布是非线性的样本,需要将非线性可分特征映射到另一个空间(维度不变或变高都可),变成线性可分特征。然后才能用线性SVM来优化参数。如图下左图到右图:
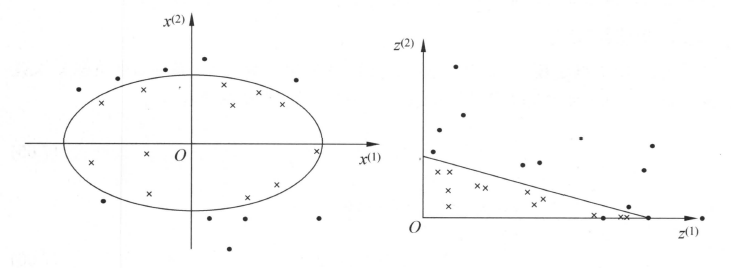
理论上需要定义确定的映射函数将输入映射成线性可分的特征,实际上这一中间环节可以隐去。下面说明这一方法。
核技巧
定义从输入空间到特征空间的映射$\phi(x):\mathcal{X}\to \mathcal{H}$,观察线性可分SVM的对偶问题和最终的判别函数,里面关于样本特征之间的运算都是内积。因此映射后的线性可分的样本特征要做的同样是内积。定义这一内积为:
$K(x,z)=<\phi(x),\phi(z)>$,后面内积直接用$\phi(x)\phi(z)$表示
样本的维度比较小还好,比如上图的二维,可以直接想出一个映射,但是当维度很高时就很难想了。因此想到,可以跳过定义映射,直接定义这个$K(x,z)$,称之为核函数。
那么什么样的核函数一定可以表示成两个映射后的向量的内积呢?首先映射函数$\phi$是可以任意定义的,因此$K(x,z)$的限制主要来自于内积运算的性质。我们把这样的核函数叫做正定核。
正定核的充要条件
设$K:\mathcal{X}\times\mathcal{X}\to R$为对称函数,则$K(x ,z) $为正定核函数的充要条件是:
对任意$x_i \in \mathcal{X}, i=1, 2,..., n, K(x, z) $对应的Gram 矩阵
$ \left[ \begin{matrix} K(x_1,x_1)&\cdots&K(x_1,x_n)\\ \vdots&&\vdots\\ K(x_n,x_1)&\cdots&K(x_n,x_n)\\ \end{matrix} \right]\succeq 0$
$\succeq 0$表示半正定。具体证明请看《统计学习方法》P136~139。
常用正定核
线性核(即直接内积):
$K(x,z)=xz$
多项式核:
$K(x,z)=(xz+1)^p$
高斯核:
$\displaystyle K(x,z)=\exp(-\frac{||x-z||^2}{2\sigma^2})$
使用核函数后,待优化的对偶问题变为:
$ \begin{array}{lcl} \min\limits_{\alpha}\displaystyle\frac{1}{2}\sum\limits_{i=1}^{N}\sum\limits_{j=1}^{N}\alpha_i\alpha_jy_iy_jK(x_i,x_j)-\sum\limits_{i=1}^{N}\alpha_i \\ \begin{aligned} \text{s.t.}\;&\sum\limits_{i=1}^{N}\alpha_iy_i=0\\ &0\le\alpha_i\le C,\;\;i = 1,2,...,N \end{aligned} \end{array} $
分类决策函数变为:
$\displaystyle f(x) = \text{sign}\left(\sum\limits_{i=1}^{N}\alpha^*_iy_iK(x_i,x)+b^*\right)=\text{sign}\left(\sum\limits_{i\in S}\alpha^*_iy_iK(x_i,x)+b^*\right)$
即原来的直接内积$x_ix$变成了先映射再内积的$K(x_i,x)$。其中$S$为支持向量集合($\alpha$不为0的样本集合,即2.2支持向量中的2~5)。
然而,选择合适的正定核以使输入映射成线性可分还需要作其它的努力。。。。。。。。。。
SMO算法
正如前面所说,在对偶问题中,$\alpha$需要分类讨论的情况数随着样本量的增大以指数级上升(即每个$\alpha$是否为0),SMO(sequential minimal optimization)算法可以加快对偶问题的优化。它采用迭代的方式,每次将待优化问题分离出一个小问题求解,最终求解原问题。
具体流程
初始化
初始化所有的$\alpha_i$为常数(通常为0),此时这些$\alpha_i$满足对偶问题的两个不等式约束:
$\begin{gather}&\sum\limits_{i=1}^{N}\alpha_iy_i=0\\ &0\le\alpha_i\le C,\;\;i = 1,2,...,N\\ \label{}\end{gather}$
实际上就是满足KKT条件的1和4,因为$(13)$是条件1使梯度为0得出的,$(14)$是条件1和4共同得到的。但是,它们并不一定同时满足KKT条件的2和3(因为原问题没有等式约束,所以没有条件5):
$\begin{gather}\displaystyle\alpha_i(1-\xi_i-y_i(\sum\limits_{j=1}^N\alpha_jy_jK_{ji}+b))=0\label{}\end{gather}$
$\begin{gather}\displaystyle1-\xi_i-y_i(\sum\limits_{j=1}^N\alpha_jy_jK_{ji}+b)\le0\label{}\end{gather}$
也就是:
$\begin{gather}y_i(\sum\limits_{j=1}^N\alpha_jy_jK_{ji}+b)\left\{\begin{aligned}&\ge1,\;\;\alpha_i=0\\&=1,\;\;0<\alpha_i<C\\&\le1,\;\;\alpha_i=C\\\end{aligned}\right.\label{}\end{gather}$
如果条件2和3也都满足的话,就迭代结束,也就达到最终的解了。其中每次迭代都会保持$(13),(14)$两个约束成立。
迭代优化
每次迭代,选出最“不好”的两个$\alpha$来进行优化,固定剩下的$N-2$个$\alpha$(这样的操作有点像小批量梯度下降)。如何才算“不好”的$\alpha$放后面讲,因为选择$\alpha$基于优化的效率,为了说明效率所在,所以先说优化。
不失一般性,假设选择的两个变量是$\alpha_1,\alpha_2$。则这个子问题可以写为(最小化中将与$\alpha_1,\alpha_2$无关的项去了):
$\begin{array}{lcl} \begin{aligned} \min\limits_{\alpha_i,\alpha_2}W(\alpha_1,\alpha_2) = &\frac{1}{2}K_{11}\alpha_1^2+\frac{1}{2}K_{22}\alpha_2^2+y_1y_2K_{12}\alpha_1\alpha_2-\\ &(\alpha_1+\alpha_2)+y_1\alpha_1\sum\limits_{i=3}^Ny_i\alpha_iK_{i1}+y_2\alpha_2\sum\limits_{i=3}^Ny_i\alpha_iK_{i2} \\ \end{aligned}\\ \begin{aligned} \text{s.t.}\;\;&\alpha_1y_1+\alpha_2y_2 = -\sum\limits_{i=3}^Ny_i\alpha_i = \varsigma\\ &0\le\alpha_i\le C,\;\;\;i=1,2 \end{aligned} \end{array}$
由$(13)$式,$\alpha_1$又可以被$\alpha_2$表达,于是这个子优化就变为一个带约束的一元二次函数最值问题,初中生的题目。主要操作就是先用导数求出二次函数的驻点,如果在约束内就为最终解,在约束外就选约束中与之较近的端点为解。尽管这么简单,但是为了后面的选择,还是要推导一下。约束可以在二维坐标系中表示出来:
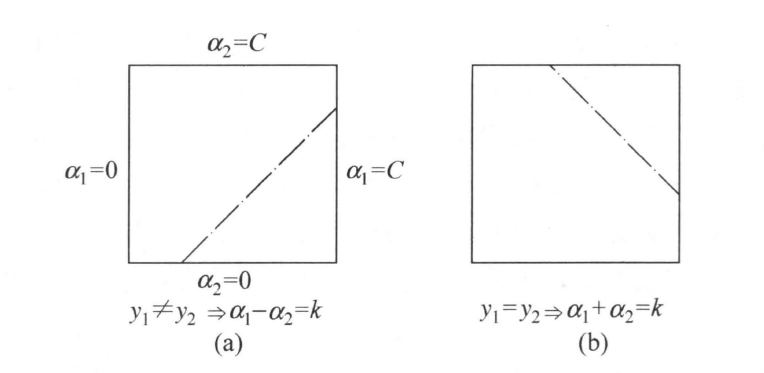
因为$y_1,y_2$绝对值为1,所以只要关于它们的符号进行分类。分成两种情况,$y_1\ne y_2$和$y_1=y_2$,于是可取的点分别如上图a、b中斜线所示。设$\alpha_2$取值为$[L,H]$,则当$y_1\ne y_2$时
$L=\max(0,\alpha_2-\alpha_1),H=\min(C,C+\alpha_2-\alpha_1)$
你可能会有为什么不用$\varsigma$而用$\alpha_2-\alpha_1$来算的疑问。这是因为每次迭代都保持$(13)$的成立,因此直接用$\alpha_2-\alpha_1$方便,而$\varsigma$需要算$N-2$个求和。又因为计算时利用了$(13),(14)$,所以这样算出来的$\alpha_1,\alpha_2$依然能维持$(13),(14)$的成立。当$y_1=y_2$时
$L=\max(0,\alpha_2+\alpha_1-C),H=\min(C,\alpha_2+\alpha_1)$
然后就是简单的先替换$\alpha_1$,再求导等于0,整理后得到:
$(K_{11}+K_{22}-2K_{12})\alpha_2^*=(K_{11}+K_{22}-2K_{12})\alpha_2+y_2(E_1-E_2)$
其中
\begin{gather} \displaystyle E_i=\left(\sum\limits_{j=1}^N\alpha_iy_iK(x_j,x_i)+b\right)-y_i \label{} \end{gather}
$E_i$理解为预测函数对$x_i$的预测值与其真实标签$y_i$之差。再定义
$ \eta = K_{11}+K_{22}-2K_{12}$
$\eta$理解为$x_1,x_2$映射到特征空间中的向量之间的距离(距离二范的平方),于是
$\begin{gather}\displaystyle\alpha_2^*=\alpha_2+\frac{y_2(E_1-E_2)}{\eta}\label{}\end{gather}$
然后更新$\alpha_2,\alpha_1$:
$ \alpha_2^{update}= \left\{ \begin{aligned} &H,&\alpha_2^*>H\\ &\alpha_2^*,&L\le\alpha_2^*\le H\\ &L,&\alpha_2^*<L\\ \end{aligned} \right. $
$\alpha_1^{update} = (\varsigma - \alpha_2^{update}y_2)y_1 = \alpha_1+y_1y_2(\alpha_2-\alpha_2^{update})$
最后还有$(18)$的$b$的计算,《统计学习方法》对$b$的计算感觉没有说清楚。
在我理解,这个$b$的更新就是用更新后的$\alpha_1$或$\alpha_2$,看哪个在$(0,C)$区间,就用KKT条件2式即$(15)$直接计算$b$;如果两个$\alpha$都是0或$C$,则取依然用$(15)$计算两个$b$,取这两个$b$的平均值。
我的疑问是:首先,更新完$\alpha_1,\alpha_2$后,$\alpha_1,\alpha_2$是否保证满足$(15),(16)$式呢,也就是没说明能不能用$(15)$来算$b$?其次,假设它们更新完后满足$(15),(16)$式,但是如果$\alpha_1,\alpha_2$都不在$(0,C)$区间为什么还能用$(15)$来算$b$呢?最后,书中只说了更新$b$,刚开始的$b$初始化为多少呢?还请懂的大佬不吝赐教。
变量的选择
变量的选择就是先遍历所有的$\alpha_i$,查看哪个$\alpha_i$违反$(17)$最严重,作为待更新的$\alpha_1$;然后再选择使$(19)$中的$|E_1-E_2|$最大的$\alpha_2$,以使$\alpha_2$变化最大。
人脸识别实验
接下来使用PCA(点击链接)与SVM实现人脸识别。大致流程如下:
0、对人脸数据集预处理。
1、将所有训练集人脸存在矩阵中,每行一张人脸照片。
2、使用PCA对矩阵行降维,提取特征(用于降维、提取特征的矩阵就是所谓“特征脸”)。
3、选择SVM的核函数为高斯核,再选择一组超参数(软间隔权重C、高斯核的方差)来交叉验证。
4、用降维后的人脸矩阵交叉验证得到最优超参数。
5、用降维人脸矩阵训练使用最优超参数的SVM,得到训练完成的SVM。
6、把以相同方式存在矩阵中的测试集人脸,先用前面获得的特征脸降维,再用训练好的SVM测试,统计数据。
用于训练与测试的人脸集如下图:

数据预处理代码:
import matplotlib.pyplot as plt import numpy as np import pylab import os img = plt.imread("face.jpg")#人脸图片 fig = plt.figure() ax = fig.add_subplot(111) print(img) def split_img(img): a = np.zeros([400,56,46,3]) ##57*47 for i in range(20): for j in range(20): a[i*20+j] = img[i*57:(i+1)*57-1,j*47:(j+1)*47-1] return a def output_img(imgs): for i in range(len(imgs)): if not os.path.exists("faces/"+str(int(i/10))): os.mkdir("faces/"+str(int(i/10))) plt.imsave("faces/"+str(int(i/10))+"/"+str(i%10)+".jpg",imgs[i]) b = split_img(img) b = b/255 output_img(b) ax.imshow(b[0]) ax.axis("off") pylab.show()
数据获取(与训练测试代码存在同目录即可,不用执行):
import matplotlib.pylab as plt import numpy as np def get_train_data(): faces_train = np.zeros([40,6,56,46,3]) #56*46 train_name = np.zeros([40,6]).astype(int) faces_test = np.zeros([40,4,56,46,3]) #56*46 test_name = np.zeros([40,4]).astype(int) for i in range(40): for j in range(6): faces_train[i,j] = plt.imread("faces/"+str(i)+"/"+str(j)+".jpg") train_name[i,j] = i for i in range(40): j = 6 while j<10: faces_test[i,j-6] = plt.imread("faces/"+str(i)+"/"+str(j)+".jpg") test_name[i,j-6]=i j+=1 faces_train = faces_train[:,:,:,:,0].reshape([240,56,46])/255 faces_test = faces_test[:,:,:,:,0].reshape([160,56,46])/255 train_name = train_name.reshape([240]) test_name = test_name.reshape([160]) train_data = {"data":faces_train,"name":train_name} test_data = {"data":faces_test,"name":test_name} print("数据初始化成功!") return train_data,test_data
模型训练与测试:
#%% 训练模型获取数据 from get_data import * import matplotlib.pylab as plt import numpy as np import pylab from sklearn.decomposition import PCA from sklearn.svm import SVC from sklearn.pipeline import make_pipeline import seaborn as sns plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签 plt.rcParams['axes.unicode_minus']=False #用来正常显示负号 train_data,test_data = get_train_data() #获取数据图像56*46,训练集240,测试集160 #%%训练模型 #模型选择,加入管道 pca = PCA(n_components = 50,whiten=True) svc = SVC(kernel='rbf',class_weight="balanced") model = make_pipeline(pca,svc) #以下交叉验证选择最优超参数 print("正在交叉验证寻找最优超参数。。。") from sklearn.model_selection import GridSearchCV param_grid = {"svc__C":[50,60,70,80],"svc__gamma":[0.0001,0.0005,0.001,0.005]}#定义软间隔权重、高斯核方差 grid = GridSearchCV(model,param_grid,cv = 6)#交叉验证6折,因为每个人的脸有6张,所以也是留一法 grid.fit(train_data["data"].reshape(240,56*46),train_data["name"])#用训练集交叉验证,选择最优超参数 print("最优参数已找到:") print(grid.best_params_) print("用最优超参数训练模型。。。") model = grid.best_estimator_ #用最优超参数训练模型 model.fit(train_data["data"].reshape(240,56*46),train_data["name"]) #%%测试模型 print("训练完毕,开始测试。。。") yfit = model.predict(test_data["data"].reshape([160,56*46])) print("测试完毕,数据统计:") from sklearn.metrics import classification_report print(classification_report(test_data["name"],yfit)) print("绘制预测结果图。。。。") fig = plt.figure(figsize=(100,100)) for i in range(10): for j in range(16): ax = fig.add_subplot(10,16,i*16+j+1) ax.imshow(test_data["data"][i*16+j],cmap="bone") ax.set(xticks =[],yticks = []) ax.set_ylabel(yfit[i*16+j],size = 10) pylab.show() print("绘制混淆矩阵。。。。") from sklearn.metrics import confusion_matrix mat = confusion_matrix(test_data["name"],yfit) sns.heatmap(mat.T,square= True,annot=True,fmt="d",cbar=False) plt.xlabel("真实标签") plt.ylabel("预测标签") pylab.show()


