LDA——线性判别分析基本推导与实验

介绍与推导

　　LDA是线性判别分析的英文缩写，该方法旨在通过将多维的特征映射到一维来进行类别判断。映射的方式是将数值化的样本特征与一个同维度的向量做内积，即：

$y=w^Tx$

　　因此，建立模型的目标就是找到一个最优的向量，使映射到一维后的不同类别的样本之间“距离”尽可能大，而同类别的样本之间“距离”尽可能小，使分类尽可能准确。

　　具体来说，就是使映射后类内样本方差尽可能小，类间样本方差尽可能大。也就是（这里为二分类，多分类类似）：

$ \begin{align*} &\quad \min\limits_w \left[\sum\limits_{x\in X_0}(w^Tx-w^T\mu_0)^2+\sum\limits_{x\in X_1}(w^Tx-w^T\mu_1)^2\right]\\ &=\min\limits_w w^T \left[\sum\limits_{x\in X_0}(x-\mu_0)(x-\mu_0)^T+\sum\limits_{x\in X_1}(x-\mu_1)(x-\mu_1)^T\right]w \\ &=\min\limits_w w^TS_ww \\ \end{align*} $

　　和

$ \begin{align*} &\quad \max\limits_w \left[(w^T\mu_0-\frac{w^T\mu_0+w^T\mu_1}{2})^2+(w^T\mu_1-\frac{w^T\mu_0+w^T\mu_1}{2})^2\right]\\ &=\max\limits_w \frac{1}{2}w^T(\mu_0-\mu_1)(\mu_0-\mu_1)^Tw\\ &=\max\limits_w \frac{1}{2}w^TS_bw \\ \end{align*}  $

 　　因为自变量只有$w$，不一定二者都能同时达到最优，所以整合到一起取下式的最大值：

$J = \displaystyle \frac{w^TS_bw}{w^TS_ww}$

 　　也就是：

$ \begin{align*} &\min\limits_w -w^TS_bw\\ &\text{s.t.}\,\, w^TS_ww = 1 \end{align*}   $

 　　因为$S_w$正定，$S_b$半正定，所以使用拉格朗日乘子法（点击链接），最终得到：

$w = S_w^{-1}(\mu_0-\mu_1)$

　　其中$S_w^{-1}$是$S_w$的伪逆。

实验

西瓜数据集

　　实验用数据集为西瓜数据集：  

　　将数据填入Excel中后，在python中读取，然后使用处理好的数据计算出$w$，最后进行测试。

　　各个样本点、映射平面以及映射后的样本点如下图所示：

 

　　可以看到两类的样本点明显不是线性可分的，因此，不论如何选取一次的线性映射，都不可能将两类样本完全分开。而找到的映射平面将样本映射到一维后（即在右图的Z轴上），依然是很多不同类别的点穿插在一起。

　　因此，判别训练集的正确率较低：

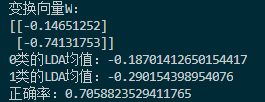
　　仅0.7。

线性数据集

　　为了测试LDA在线性可分特征数据集上的性能，以二维正态分布生成如下样本点：

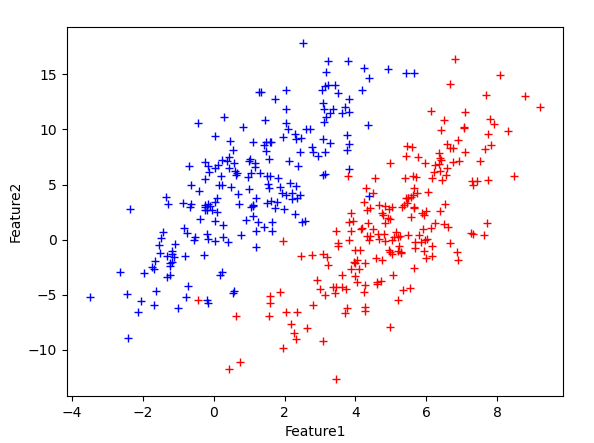
 　　其中蓝色点均值为$[1,5]$，红色为$[5,1]$；两类样本的协方差矩阵都为：

$\left[\begin{matrix}1.4&1\\1&5\\\end{matrix}\right]$

 　　映射图如下：

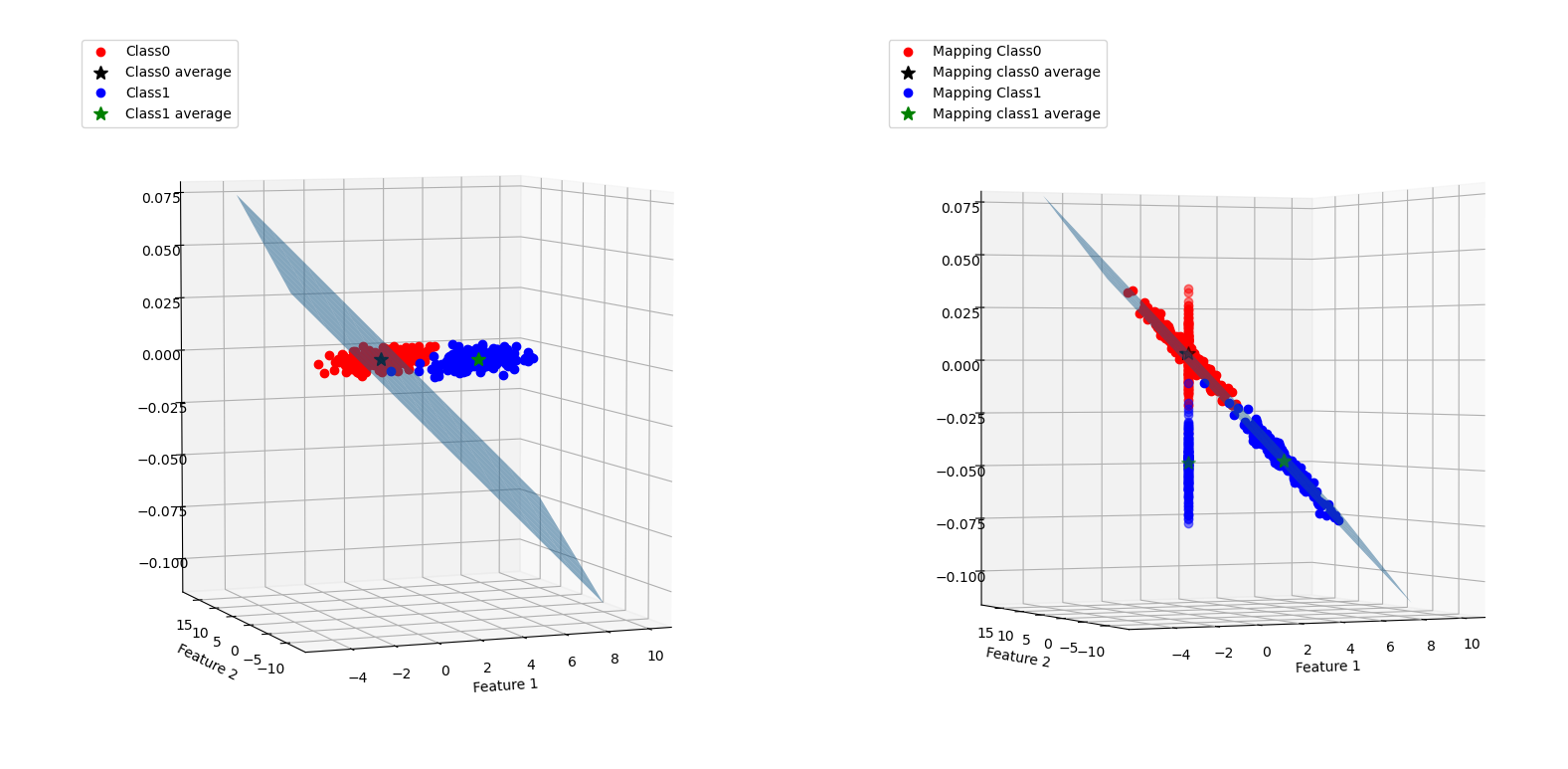
　　判断结果如下：

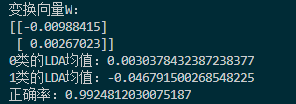
　　正确率提高到了0.99，可见LDA在线性可分数据上的性能还是不错的。

实验代码

　　LDA代码（数据输入data.xlsx中第一个表即可）：

#%%
import matplotlib.pyplot as plt
import numpy as np 
import xlrd 

table = xlrd.open_workbook('test.xlsx').sheets()[0]#读取Excel数据
data = []
for i in range(1,table.nrows):#假设第一行是表头不读入
    data.append(table.row_values(i))  
class0 = []
class1 = []
#划分正反特征集，编号第一列，类别最后一列，特征在中间
for i in data:
    if i[-1] == 0:
        class0.append(i[1:-1])
    else:
        class1.append(i[1:-1])
data = np.array(data) #转为数字矩阵
class0 = np.array(class0) #特征都是行向量，组成矩阵
class1 = np.array(class1) 

# %%
#计算相应类别特征的平均
n0 = len(class0)
n1 = len(class1)
miu0 = np.dot(np.ones([1,n0]),class0)/n0
miu1 = np.dot(np.ones([1,n1]),class1)/n1 

#%%
#计算类内散度矩阵
s0 = class0 - miu0  
s1 = class1 - miu1
Sw = np.dot(s0.transpose(),s0)+np.dot(s1.transpose(),s1)  
W = np.dot(np.linalg.pinv(Sw),(miu0-miu1).transpose()) #计算W
#输出W、miu0和miu1在映射后的值
miu0_LDA = np.dot(miu0,W)
miu1_LDA = np.dot(miu1,W)
print("变换向量W：")
print(W)
print("0类的LDA均值："+str(miu0_LDA[0,0]))
print("1类的LDA均值："+str(miu1_LDA[0,0]))

#%%
#判断类别
c_discrim = np.dot(data[:,1:-1],W)  
#统计正确率
right = 0
for i in range(len(data)):
    if np.abs(miu0_LDA[0,0] - c_discrim[i]) < np.abs(miu1_LDA[0,0] - c_discrim[i]):
        if data[i][-1] == 0:
            right +=1 
    else:
        if data[i][-1] == 1:
            right +=1 
print("正确率："+str(right / len(data)))

#%%
#画图(仅适用于二维特征) 
##################图一
fig = plt.figure() 
ax = fig.add_subplot(121,projection = '3d')  
plt.xlabel("Feature 1")
plt.ylabel("Feature 2") 
ax.plot(class0[:,0],class0[:,1],'o',label = 'Class0',color = "red") #0类
ax.plot([miu0[0,0]],[miu0[0,1]],'*',label = 'Class0 average',color = "black",markersize = 10) #0类平均
ax.plot(class1[:,0],class1[:,1],'o',label = 'Class1',color = "blue") #1类  
ax.plot([miu1[0,0]],[miu1[0,1]],'*',label = 'Class1 average',color = "green",markersize = 10) #1类平均  
#映射平面
t = np.linspace(-5,10,10) 
X,Y = np.meshgrid(t,t)
ax.plot_surface(X,Y,X*W[0]+Y*W[1],alpha = 0.5)
ax.legend(loc = 'upper left')

##################图二
ax = fig.add_subplot(122,projection = '3d')  
plt.xlabel("Feature 1")
plt.ylabel("Feature 2") 
ax.plot(class0[:,0],class0[:,1],np.dot(class0,W)[:,0],'o',label = 'Mapping Class0',color = "red") #0类映射
ax.plot([miu0[0,0]],[miu0[0,1]],np.dot(miu0[0],W),'*',label = 'Mapping class0 average',color = "black",markersize = 10) #0类平均映射
ax.plot(class1[:,0],class1[:,1],np.dot(class1,W)[:,0],'o',label = 'Mapping Class1',color = "blue") #1类映射
ax.plot([miu1[0,0]],[miu1[0,1]],np.dot(miu1[0],W),'*',label = 'Mapping class1 average',color = "green",markersize = 10) #1类平均映射
ax.plot(np.zeros([len(class0)]),np.zeros([len(class0)]),np.dot(class0,W)[:,0],'o',color = "red",alpha = 0.5)  #0类映射值
ax.plot(np.zeros([len(class1)]),np.zeros([len(class1)]),np.dot(class1,W)[:,0],'o',color = "blue",alpha = 0.5)   #1类映射值
ax.plot([np.zeros([1])],np.zeros([1]),np.dot(miu0[0],W),'*',color = "black",alpha = 0.5,markersize = 10)  #0类平均映射值
ax.plot([np.zeros([1])],np.zeros([1]),np.dot(miu1[0],W),'*',color = "green",alpha = 0.5,markersize = 10) #1类平均映射值
#映射平面 
X,Y = np.meshgrid(t,t)
ax.plot_surface(X,Y,X*W[0]+Y*W[1],alpha = 0.5)
ax.legend(loc = 'upper left')
 
plt.show() 

　　生成线性数据集代码：

import openpyxl 
import numpy as np
import matplotlib.pyplot as plt
 
sampleNum = 200
 
# 二维正态分布
mu = np.array([[1, 5]])
Sigma = np.array([[1.4, 1], [1, 5]])
s1 = np.dot(np.random.randn(sampleNum, 2), Sigma) + mu 
plt.plot(s1[:,0],s1[:,1],'+',color='blue') 

mu = np.array([[5, 1]]) 
Sigma = np.array([[1.4, 1], [1, 5]])
s2 = np.dot(np.random.randn(sampleNum, 2), Sigma) + mu 
plt.plot(s2[:,0],s2[:,1],'+',color='red')
plt.xlabel('Feature1')
plt.ylabel('Feature2')

plt.show()
data = openpyxl.Workbook()
table = data.create_sheet('test')
table.cell(1,1,'id')
table.cell(1,2,'feature1')
table.cell(1,3,'feature2')
table.cell(1,4,'class')
for i in range(sampleNum):
    table.cell(i+2,1,i+1)
    table.cell(i+2,2,s1[i][0])
    table.cell(i+2,3,s1[i][1])
    table.cell(i+2,4,0)
for i in range(sampleNum):
    table.cell(i+1+sampleNum,1,i+1)
    table.cell(i+1+sampleNum,2,s2[i][0])
    table.cell(i+1+sampleNum,3,s2[i][1])
    table.cell(i+1+sampleNum,4,1)
data.remove(data['Sheet'])
data.save('test.xlsx')