神经网络中常用的激活函数

ReLu

$\max(0,z)$

　　修正线性单元，是最常用的非线性映射函数。常在神经网络隐层中使用，因为它在反向传播中计算导数十分方便。导数为：

$\left\{\begin{aligned}&1,z\ge0\\&0,z<0\end{aligned}\right.$

softplus

 $\log(1+e^z)$

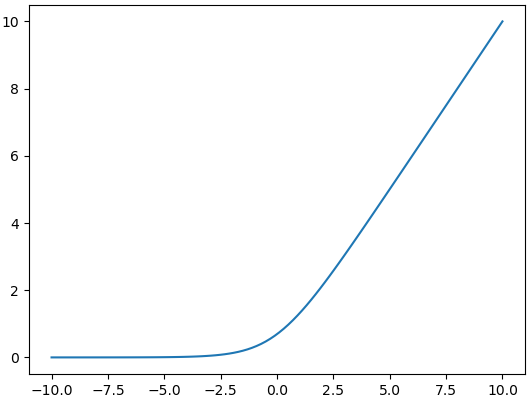
　　ReLu的“软化版”。导数为：

$\displaystyle 1-\frac{1}{e^z+1}$

sigmoid

$\displaystyle\sigma(z)=\frac{1}{1+e^{-z}}$　　

　　同样将单个输入值映射到(0,1)之间，但函数是对称的。求导也很方便，导数为：

$\displaystyle \frac{1}{1+e^{-z}} - \frac{1}{(1+e^{-z})^2} =\sigma(z)(1-\sigma(z))$

softmax

$\displaystyle\sigma(z) = \frac{e^{z_i}}{\sum_{j=1}^n e^{z_j}}$

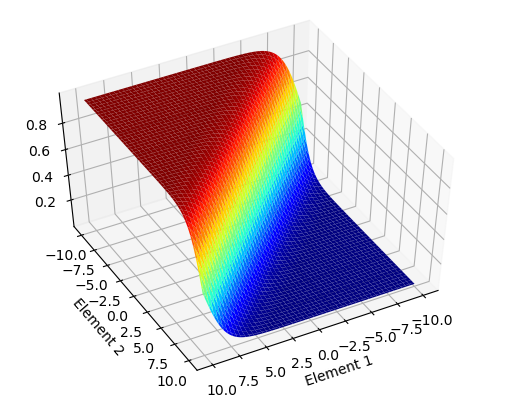
　　将一层的输出的多个值归一化，通常在预测各个类别的概率时用到，而且一般用在输出层。图类似于sigmoid，上图画的是元素数量为2的示意图。

　　比如某个模型输出层中每个结点的输出分别是：狗、猫、猪、牛，这些动物是输入数据的真实标签的概率，概率总和显然应该为1，因此用softmax来归一化。好处是所有输出一定为正值，总和为1，并且较大值能够更好地凸显出来。

　　softmax与其它激活函数最大的不同就在于，同一层每个元素的计算都涉及到该层的所有元素（$R^n\to R$），而其他激活函数都是每个元素算它们自己的（$R\to R$）。softmax的导数与sigmoid类似，复杂度也不高，但因它有“汇总”的功能，所以会分成两种情况。下面直接举个具体的例子来说明。

　　假设这个激活函数用在输出层，该层有三个结点，前一层线性运算后的结果存在向量$z$中，损失函数使用MSE，于是目标函数为（不算正则项）：

$\displaystyle L=\frac{1}{2}\left[(\sigma_1(z)-y_1)^2+(\sigma_2(z)-y_2)^2+(\sigma_3(z)-y_3)^2\right]$

　　其中

$\displaystyle\sigma_i(z) = \frac{e^{z_i}}{\sum_{j=1}^3e^{z_j}}$

　　对$z_1$进行求导：

$ \begin{aligned} &\frac{\partial L}{\partial z_1}\\ =& (\sigma_1(z)-y_1)\left(\frac{e^{z_1}}{e^{z_1}+e^{z_2}+e^{z_3}}\right)'_{z_1}+\\ &(\sigma_2(z)-y_2)\left(\frac{e^{z_2}}{e^{z_1}+e^{z_2}+e^{z_3}}\right)'_{z_1}+\\ &(\sigma_3(z)-y_3)\left(\frac{e^{z_3}}{e^{z_1}+e^{z_2}+e^{z_3}}\right)'_{z_1}\\ =&(\sigma_1(z)-y_1)\left(\frac{e^{z_1}}{e^{z_1}+e^{z_2}+e^{z_3}}-\frac{(e^{z_1})^2}{(e^{z_1}+e^{z_2}+e^{z_3})^2}\right)+\\ &(\sigma_2(z)-y_2)\left(\frac{-e^{z_1}e^{z_2}}{(e^{z_1}+e^{z_2}+e^{z_3})^2}\right)+\\ &(\sigma_3(z)-y_3)\left(\frac{-e^{z_1}e^{z_3}}{(e^{z_1}+e^{z_2}+e^{z_3})^2}\right)\\ =&(\sigma_1(z)-y_1)\sigma_1(z)(1-\sigma_1(z))+\\ &(\sigma_2(z)-y_2)[-\sigma_1(z)\sigma_2(z)]+\\ &(\sigma_3(z)-y_3)[-\sigma_1(z)\sigma_3(z)] \end{aligned} $

　　$z_2,z_3$的求导类似。可以看出，在反向传播中，当激活函数所在结点$i$与待求导的结点$j$相同时，softmax导数为：

$\begin{gather}\sigma_i(z)(1-\sigma_i(z))\label{}\end{gather}$

　　否则，导数为：

$\begin{gather}-\sigma_i(z)\sigma_j(z)\label{}\end{gather}$

　　而节点激活输出对节点输入的导数则是这两种导数的求和：一个$(1)$式，$n-1$个$(2)$式。

tanh

$\displaystyle\text{tanh}(z)=\frac{e^z-e^{-z}}{e^z+e^{-z}} $

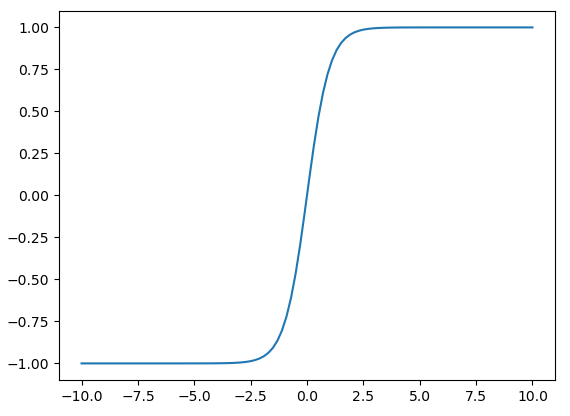
　　与sigmoid有点像，映射到(-1,1)。

　　导数为：

$\displaystyle \frac{4}{e^{2z}+1}-\frac{4}{(e^{2z}+1)^2} = 1-\text{tanh}^2(z)$ 

maxout

　　Maxout和之前的计算方式都不一样，它不像激活函数，更像是层，因为它有参数用于训练。 它在两个层中间添加Maxout层，对下一层的每一个元素都通过权重和偏执线性计算出一列向量，向量的维度$t$是超参数，然后将向量的最大值作为元素的取值。

　　如下图所示：

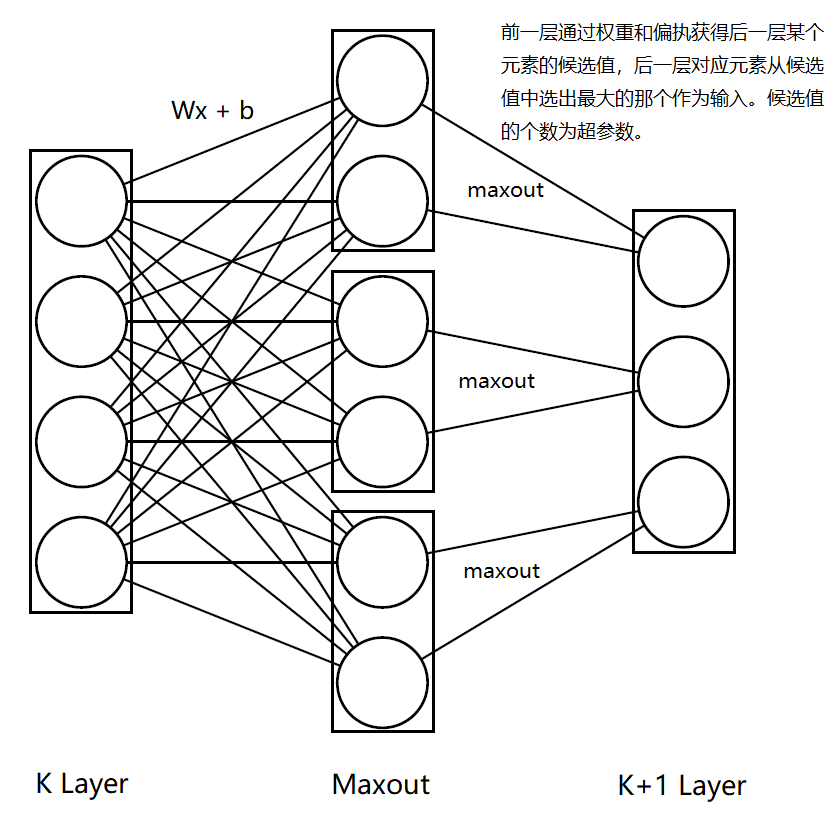　　图仅为便于理解才这么画，代码中定义参数时，并不是这样分出来定义maxout的权重和偏执的，所有权重是可以放在同一个矩阵中的。图中$t$为2，$K$层变量数为4，$K+1$层变量为3，因此maxout层的参数总量为：

$(4\times 2+2)\times 3 = 30$

　　只要变量够多，maxout可以拟合任意的凸函数。类似于（网络截图）：

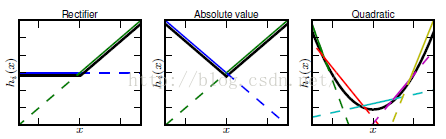
　　而凸函数后面再通过线性运算，就可以拟合任意函数了。