Python 矩阵相关
Python 中矩阵运算主要使用numpy库。NumPy的主要对象是同种元素的多维数组。这是一个所有的元素都是一种类型、通过一个正整数索引的元素表格(通常是元素是数字)。因此对于随机查找来说,比python自带的list快很多。
在numpy里面通常使用两个变量:array和matrix。其实python标准类库中也有array,但是它的功能相对numpy的少很多,所以不用。matrix是array的分支,matrix可以看做二维的array,array可以是多维,matrix和array在很多时候都是通用的。官方建议如果两个都可以用,那就选择array,因为array更灵活,速度更快,很多人把二维的array也翻译成矩阵。但是matrix的优势在于,它相对于array使用的符号更简洁一些。
矩阵和向量的创建
a = np.array([2,4,5,6,7])
如上创建了一个1*5的一行5列的array,这就相当于一个行向量(实际上不是,应该用np.array([[2,4,5,6,7]])创建)。
m = np.matrix([[1,2,4,5,6],[5,6,8,9,4]])
如上创建了一个2*5的matrix,这就是一个2*5的矩阵。
另外矩阵还可以通过这个创建:
m = np.mat([[1,2,4,5,6],[5,6,8,9,4]])
mat和matrix的相关之处是,mat([])就等同于matrix([],copy=false),而matrix([])实际上默认copy=true。
所以如果想引用一个矩阵,如m,可以使用a = mat(m),或者a = matrix(m,copy=false)。当然用[]列表来新创建一个矩阵的时候它们是完全一样的。
转置
m = m.transpose()
m = m.T
matrix和除一维外的array可以通过这个两个进行转置(T和transpose不同点暂时不研究了)。
对于一维的array,它不是矩阵,也不是向量,所以不能通过transpose来转置。因为在计算机里,二维和一维定义好以后就确定下来用几个索引标志来索引了。而向量从功能上来看,应该被看做1行或1列的矩阵,所以它应该是二维的。就是说我们索引它的某个元素,比如行向量a的第3个元素,我们应该用a[0][3],而不是a[3]。所以a = np.array([2,4,5,6,7])创建的其实啥也不是,像np.array([[2,4,5,6,7]])这样创建二维的才算真正意义上的行向量,也就能用transpose()来转置了。
如果用a = np.array([2,4,5,6,7,1,3,8])创建了一行数组a,想变成向量,要先用reshape()函数将它变成二维向量。
高维张量转置
x = np.transpose(x,(2,0,1))
以上例子是对三维张量x进行转置,(2,0,1)的意思是:将张量从(x,y,z)轴转置为(z,x,y)轴。也就是说,如果张量x的形状是[2,3,4],转换后就变成了[4,2,3]。
转置效果实际上就是将张量各个轴的顺序改变,而张量内部元素在各个轴上的索引并不会改变。也就是说,x内部有个元素索引是x[1,2,3],经过以上转置,它的索引变为了x[3,1,2],在各个轴上的索引没变,只是变了顺序。
如果不填元组参数:
x = np.transpose(x)
等价于:
x = np.transpose(x,(2,1,0))
也就是直接将三个轴顺序倒序。
更高维的张量类似。
reshape()函数
reshape()将一定规模的数组从一个形状改为另一个形状,并且不论你怎么改变形状,数组中元素的先后位置都是从一开始就确定的。用法如下:
a = np.ones([8])
a = a.reshape([2,2,2])
将原本为一维的向量a变成了2*2*2的三维立方阵。如果将a赋值给一个新变量b:
b = a.reshape([2,2,2])
a的shape不变,b是2*2*2的立方阵,而且它们共享内存,即当a改变它的元素值时,b中对应的元素也会改变。另外,因为数组的规模是固定的,因此可以有一个维度为未知,输入-1:
b = a.reshape([2,2,-1])
这样的效果和上面是一致的。
矩阵乘法
乘法有三种表达方式:*、dot()、multiply()
np.multiply()
数组或矩阵的对应位置元素相乘。

np.dot()
对于一维数组array,执行对应位置相乘,然后再求和;对于秩不为1的二维数组(array)、矩阵(matrix),执行矩阵乘法运算(超过二维的可以参考numpy库介绍)

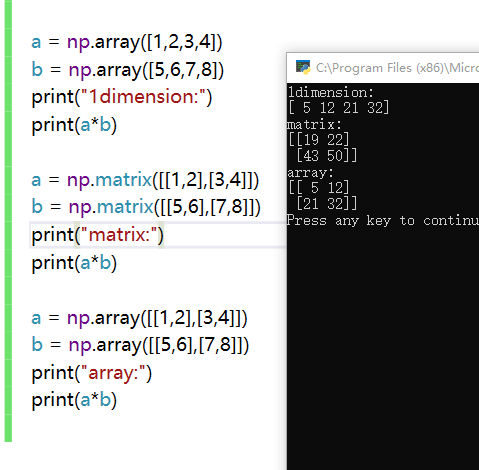
乘法运算*
对数组array执行对应位置元素相乘(相当于 np.multiply() 函数),对矩阵matrix执行矩阵乘法运算(相当于 np.dot() 函数)。就是multiply()和dot()的融合。
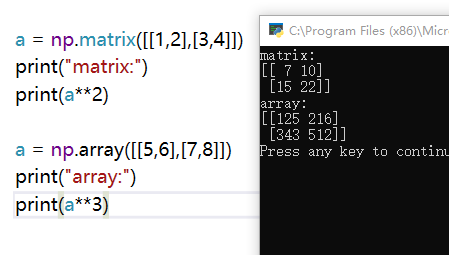
幂运算**
相当于多个array或matrix执行*,即A**3=A*A*A。
总结
multiply()全都是对应元素相乘;dot()是矩阵乘法,而一维array是对应元素相乘后之和;*对array是对应元素相乘,对matrix是矩阵乘法。
相对来说matrix注重矩阵操作,array注重阵列操作(阵中元素对应进行运算)
矩阵特征值与特征向量
np.linalg.eig(A)
返回矩阵A的特征值和特征向量数组:
np.linalg.eig(A)[0]是特征值数组,没有大小顺序;
np.linalg.eig(A)[1]是特征向量,与特征值数组相对应。


