机器学习入门(七)之----logistic回归(回归函数与概率模型)
Toast to the ones here today,
Toast to the ones we lost on the way。
现在我们讨论分类问题。主要关注目标变量为0,1的二分类问题,1为正例,0为负例。目标变量在分类问题中又称为标签。
logistic回归函数与概率模型
我们用之前回归的方法来做分类最大的问题在于预测值小于0或者大于1都是无意义的。为此我们添加如下约束,将它限制在0到1之间,
\[\begin{equation}
h_{\theta}(x)=g\left(\theta^{T} x\right)=\frac{1}{1+e^{-\theta^{T} x}}
\end{equation}
\]
\[g\left( x_1\right)=\frac{1}{1+e^{- x_1}}
\]
其中称为logistic函数,或者sigmoid函数。函数长这样,
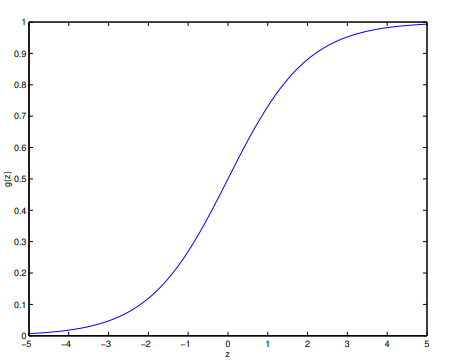
对$g\left( x_1\right) $ 不同选择会导致不同算法,以后我们会看到这个选择是非常自然的。关于这个函数的导数有如下性质,
\[\begin{equation}
\begin{aligned}
g^{\prime}(z) &=\frac{d}{d z} \frac{1}{1+e^{-z}} \\
&=\frac{-1}{\left(1+e^{-z}\right)^{2}}\frac{d}{d z}\left(e^{-z}\right) \\
&=\frac{1}{\left(1+e^{-z}\right)^{2}}\left(e^{-z}\right) \\
&=\frac{1}{\left(1+e^{-z}\right)} \cdot\left(1-\frac{1}{\left(1+e^{-z}\right)}\right) \\
&=g(z)(1-g(z))
\end{aligned}
\end{equation}
\]
现在有了logistic回归模型,怎样拟合他的参数呢?我们先给它一个概率模型,用最大似然法来拟合参数,假设给定$ x$ 标签满足二项分布,且输出0,1之间的值为标签为1的概率,则有,
\[\begin{equation}
\begin{aligned} P(y=1 | x ; \theta) &=h_{\theta}(x) \\ P(y=0 | x ; \theta) &=1-h_{\theta}(x) \end{aligned}
\end{equation}
\]
即我们假设它的预测值是样本为正例的概率值。这两个等式子可以统一起来等价地,有,
\[\begin{equation}
p(y | x ; \theta)=\left(h_{\theta}(x)\right)^{y}\left(1-h_{\theta}(x)\right)^{1-y}
\end{equation}
\]
对于一批独立样本,我们有,
\[\begin{aligned} L(\theta) &=p(\vec{y} | X ; \theta) \\ &=\prod_{i=1}^{n} p\left(y^{(i)} | x^{(i)} ; \theta\right) \\ &=\prod_{i=1}^{n}\left(h_{\theta}\left(x^{(i)}\right)\right)^{y^{(i)}}\left(1-h_{\theta}\left(x^{(i)}\right)\right)^{1-y^{(i)}} \end{aligned}
\]
老规矩,要最大化下式给出的对数似然函数,
\[\begin{aligned} \ell(\theta) &=\log L(\theta) \\ &=\sum_{i=1}^{n} y^{(i)} \log h\left(x^{(i)}\right)+\left(1-y^{(i)}\right) \log \left(1-h\left(x^{(i)}\right)\right) \end{aligned}
\]
logistic回归更新公式
和求线性回归问题时用梯度下降最小化损失函数一样,我们在此用梯度上升最大化对数似然函数(因此是加号),
\[\begin{equation}
\theta :=\theta+\alpha \nabla_{\theta} \ell(\theta)
\end{equation}
\]
还是先只考虑一个样本$ (x,y)$ ,求梯度,
\[\begin{equation}
\begin{aligned}
\frac{\partial}{\partial \theta_{j}} \ell(\theta) &=\left(y \frac{1}{g\left(\theta^{T} x\right)}-(1-y) \frac{1}{1-g\left(\theta^{T} x\right)}\right) \frac{\partial}{\partial \theta_{j}} g\left(\theta^{T} x\right) \\
&=\left(y \frac{1}{g\left(\theta^{T} x\right)}-(1-y) \frac{1}{1-g\left(\theta^{T} x\right)}\right) g\left(\theta^{T} x\right)\left(1-g\left(\theta^{T} x\right)\right) \frac{\partial}{\partial \theta_{j}} \theta^{T} x \\
&=\left(y\left(1-g\left(\theta^{T} x\right)\right)-(1-y) g\left(\theta^{T} x\right)\right) x_{j} \\
&=\left(y-h_{\theta}(x)\right) x_{j}
\end{aligned}
\end{equation}
\]
第二个等式用到sigmoid函数导数性质。因此,有如下参数更新公式,
\[\begin{equation}
\theta_j :=\theta_j+\alpha \left(y-h_{\theta}(x)\right) x_{j}
\end{equation}
\]
我们可以看到形式上更新公式和线性回归的一模一样。但这里要注意,假设函数是不同的两个函数。但这多少还是让人感到有些惊讶的。这到底是巧合,还是有更背后更深层的原因。我们在广义线性模型那里将会揭晓答案。


