学习：图论----二分图
二分图是一类比较特殊的图，图内所有的环上节点的个数是偶数（二分图中只有偶环），属于图的一种定义，除以之外还有二分图匹配，最大匹配，最大权匹配等算法。
二分图的定义
二分图内的所有环都为偶环，即在一个有向图 G=(V, E) 中，所有的顶点可以分成两个集合，使得所有的边全部都满足两边的顶点分别位于不同的集合。
下面的图都是二分图
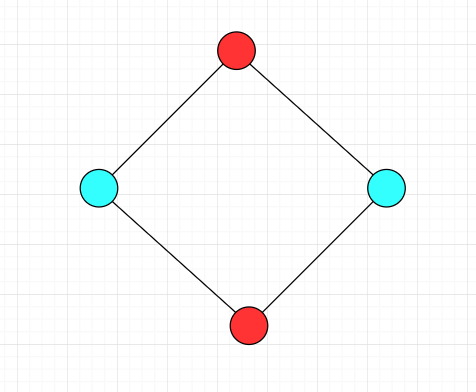
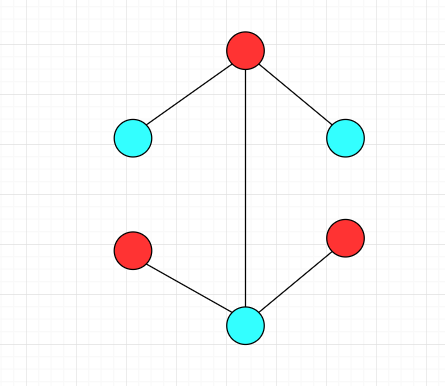
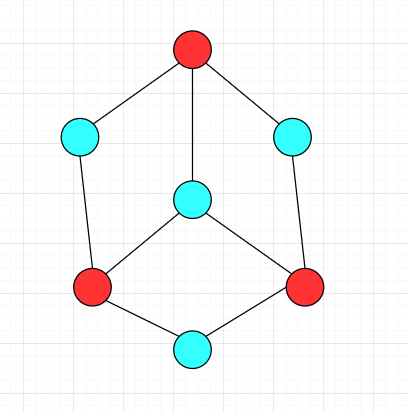
证明图 G=(V,E) 中所有环都为偶环是图 G=(V,E) 是二分图的充要条件：
1.必要性（如果G=(V,E)是二分图，则图G内所有环全为偶环）
设二分图G为G=(X,Y,E)，其中X,Y为图中顶点拆分为的两个集合，设环C为 $\left\{v_0, v_1, v_2, ..., v_k\right\}$，则环的长度为 $k$，根据二分图性质可以得 $v_i$ 相间的出现与 X 和 Y 中，假如设 $\left\{v_0, v_2, v_4, ...., v_k\right\}\subseteq X, \left\{v_1, v_3, v_5, ..., v_{k-1}\right\}\subseteq Y$，则 $k$ 为偶数，所以环C是偶环。
2.充分性（如果图G=(V,E)内的环全为偶环，则G为二分图）
在图G中任取一个点 $v$ ，将图中所有点划分为两个集合，集合 $X= \left\{v_i|v_i 与 v 的距离为偶数 \right\}$，$Y=E-X$，假设存在一条边 $(v_i, v_j)$ ，且 $v_i, v_j$ 都是 $X$ 集合内的点，那么会形成 $v$ 到 $v_i$ 到 $v_j$ 到 $v$ 的一个环，很明显环的长度为奇数不满足集合 $X$ 的条件，则说明边 $(v_i, v_j)$ 不存在，同理对于集合 $Y$ 也可以证明集合内任意两个点之间没有边，说明图G是一个二分图（分为X集合和Y集合）
图的匹配与二分图的匹配
图的匹配到底指什么了？假设对于一个图G=(V,E)，刚开始图中的顶点都是未匹配的顶点，如果我们任取一个未匹配的顶点，假设存在另一个未匹配的顶点，使得两个顶点之间有一条边连接，于是这两个未匹配的顶点可以通过这条边匹配起来，这就叫构成一个图的匹配。
很明显，二分图的顶点可以分成两个集合 $X$ 与 $Y$，对于集合 $X$ 内的任意一个点，如果要形成一个匹配，那么只能在集合 $Y$ 中寻找一个未匹配的点来尝试构成匹配。这点是二分图匹配较一般图匹配来说较未容易的地方。
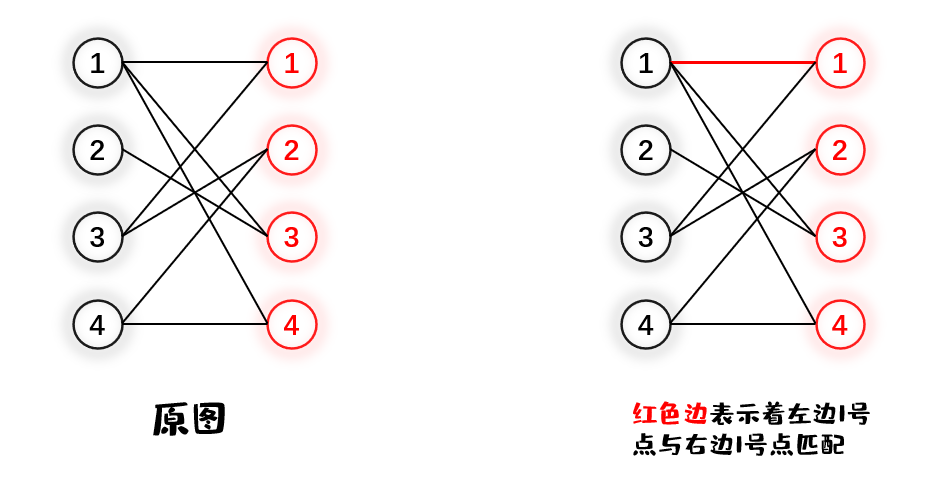
每个点都有可能找到与他匹配的一个点，但是我们可能尽可能的在一个二分图中找到尽量多的点对匹配。当找到了最多的点对匹配，我们就称这个是此二分图的最大匹配。如下图所示
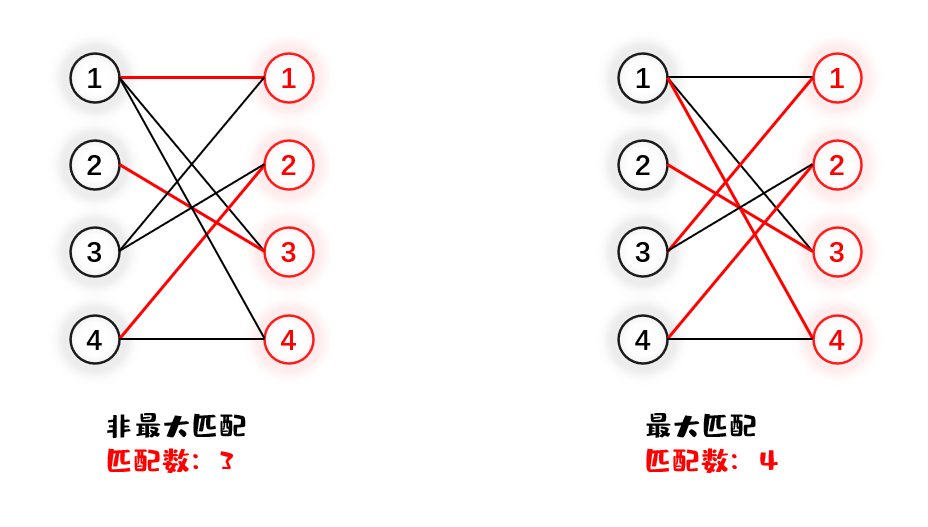当然，一个二分图的最大匹配不是惟一的
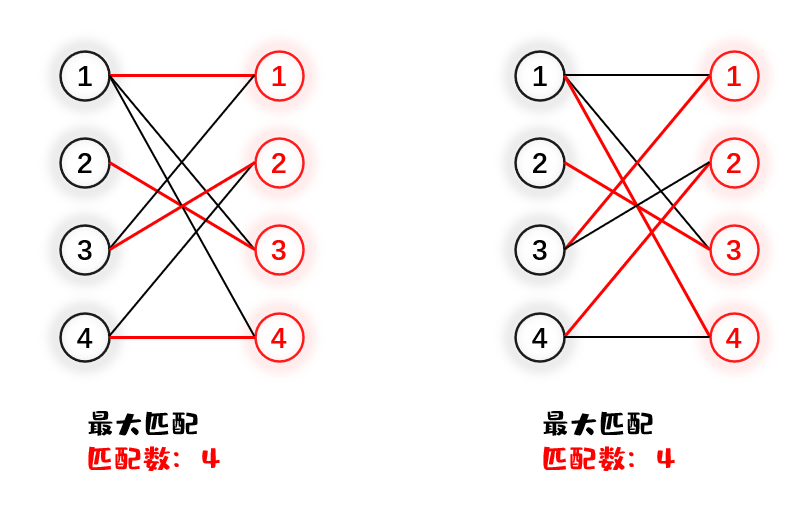
二分图最大匹配与匈牙利算法
很多时候，我们只需要算二分图的最大匹配数，这个时候就需要用到匈牙利算法。
首先要引入几个概念，设 $G=(V,E)$ 是一个无向图。如顶点集 $V$ 可分割为两个互不相交的子集 $V_1, V_2$，选择这样的子集中边数最大的子集为图的最大匹配问题。
如果一个匹配中，$|V_1|\le |V_2|$ 且匹配数 $|M|=|V_1|$，则称此匹配为完全匹配，也称完备匹配。特别的当 $|V_1|=|V_2|$ 称为完美匹配
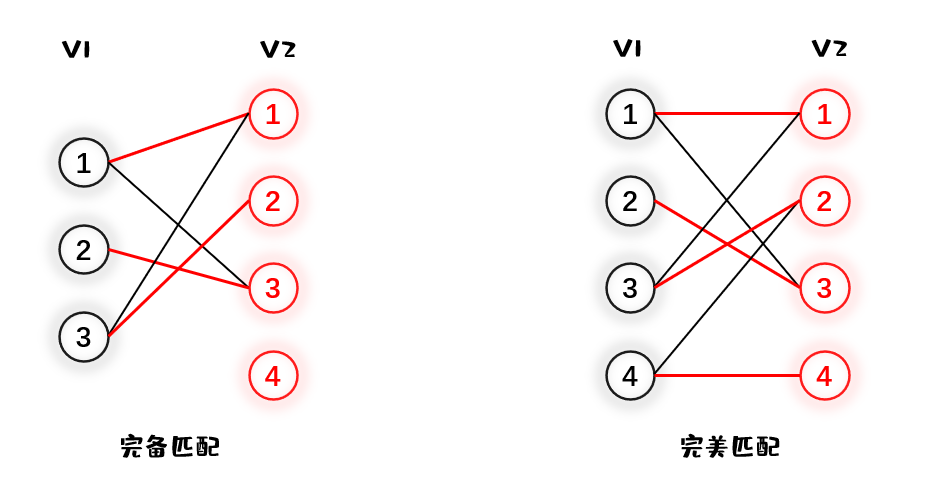
交错路：如果图上的一条路径中的边交替表现为一条匹配边和非匹配边，则称这是一条交错路。更准确的来说，我们设 $M$ 表示图的匹配边集合（也称 $M$ 为图的一个匹配），$p$ 是 $G$ 上的一条通路，如果 $p$ 中的边为属于 $M$ 的边与不属于 $M$ 的边交替出现，则称 $p$ 为一条交错路。
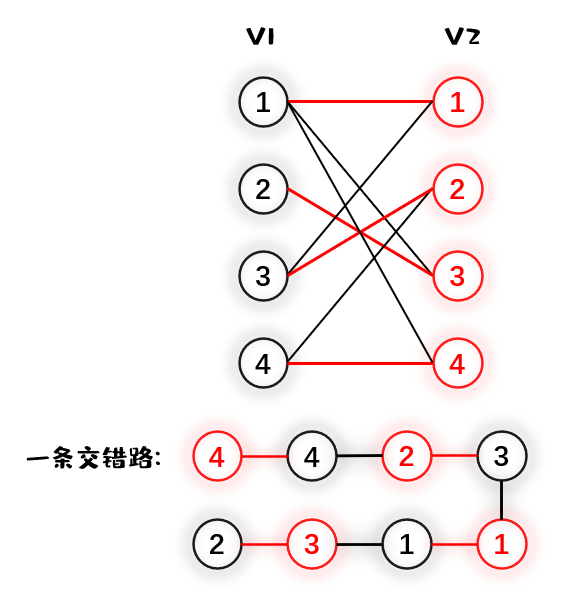
再来说一说匈牙利算法的思想，主要想法是给集合 $V_1$ 中的点尽可能多的在 $V_2$ 中寻找点进行配对。
下面是对匈牙利算法步骤一个模拟，更好的感觉算法过程：
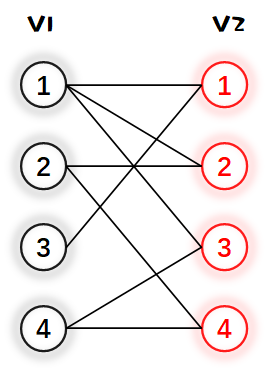
1.先给 $V_1$ 的1号节点找匹配边，从小到大遍历与1号点连接的 $V_2$ 内的点，发现 $V_2$ 内1号点可以与它配对，于是
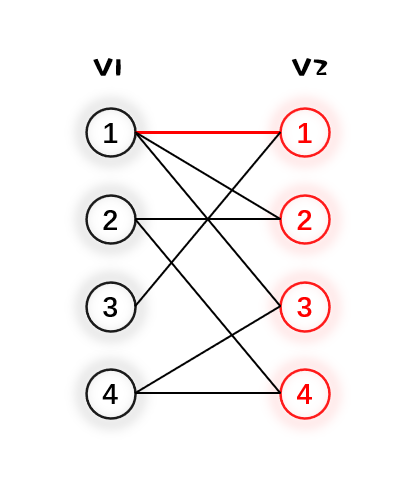
2.然后给 $V_1$ 的2号点找匹配，发现 $V_2$ 内2号点能够与之匹配，于是
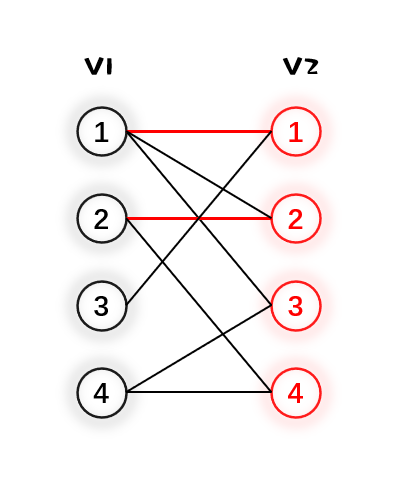
3.然后给 $V_1$ 的3号点找匹配，发现与它唯一相连的 $V_2$ 内的1号点已经被匹配了。可以观察到与 $V_2$ 的1号点匹配的是 $V_1$ 的1号点，于是我们可以尝试给 $V_1$ 的1号点换一个匹配点，于是第二个与 $V_1$ 1号点相连的是 $V_2$ 的2号点。但是 $V_2$ 的2号点也已经被匹配了（被 $V_1$ 的2号点匹配），所以我们继续又给 $V_1$ 的2号点找匹配，很明显可以将 $V_2$ 的4号点与之匹配，那么最后的结果是 $V_1$ 的2号点与 $V_2$ 的4号点匹配，$V_1$ 的1号点与 $V_2$ 的2号点匹配，最后 $V_1$ 的3号点与 $V_2$ 1号点匹配。
上图总结来说，目的是给 $V_1$ 的3号点找匹配，找匹配的过程中需要给 $V_1$ 的1号点找新的匹配，给 $V_1$ 的1号点找新匹配的过程中，又需要给 $V_1$ 的2号点找新匹配，这是一个递归的过程，当新匹配找完之后又回溯到给 $V_1$ 的3号点找匹配。
时间戳优化：
在给 $V_1$ 的1号点找新匹配时，很明显需要跳过旧匹配的连接点，但是给 $V_1$ 的1号点遍历链接的点时，是按照 $V_2$ 内的点从大到小或者从小到大的顺序遍历的，在遍历到新匹配点（$V_2$ 的2号点）之前，我们已经遍历到了 $V_2$ 的1号点，而 $V_2$ 的1号点是一个旧匹配点，需要跳过。
这时就需要引入一个叫时间戳的概念，算法一开始时先遍历 $V_1$，每次遍历一个点时间戳就加一。我们一开始给 $V_1$ 1号点找匹配点，这个时候时间戳是1，给 $V_1$ 2号点找匹配点时时间戳为2，依次类推。
每次给 $V_1$ 内的点找匹配点时，需要遍历 $V_2$ 内的点，我们创建一个 $vis$ 的数组，$vis[i]$ 表示最后一次访问 $V_2$ 内的 $i$ 号点是哪一个时间戳（初始化全为0）。
现在回过头来看为啥在给 $V_1$ 的3号点找匹配时（此时时间戳为3），需要给 $V_1$ 的1号点找新匹配，是因为遍历 $V_1$ 的3号点的连接点时，第一个找到了 $V_2$ 的1号点，于是我们将 $vis[i] = 3$，表示$V_2$ 的1号点最后一次访问时时间戳为3，而此点已经和 $V_1$ 的1号点匹配了，所以要找新匹配（注意不一定能找得到）。在给 $V_1$ 的1号点找新匹配时，我们又再次访问到了 $V_2$ 的1号点，但是此时 $vis[1] = 3$，和此时的时间戳的值相同，于是就跳过此点，重新找新的点，这样就完美跳过了旧匹配的点。
for(int i = 1; i <= n; i++){ tim++; //tim表示此时时间戳 if(dfs(i)) ans++; }int dfs(int u){ for(int i = head[u]; ~i; i = edge[i].next){ int v = edge[i].v; if(vis[v] == tim) continue; //时间戳和此时相同，跳过 vis[v] = tim; //更新时间戳 if(pre[v] == 0 || dfs(pre[v])){ //dfs(i)表示给 v2 的 i 号点找匹配 pre[v] = u; return 1; } } return 0; }
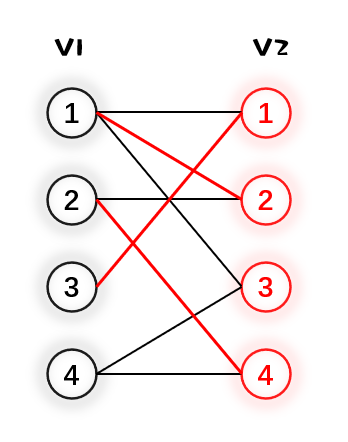
4.最后 $V_1$ 的4号点和 $V_2$ 的3号点匹配，达成了最大匹配，结束匈牙利算法。
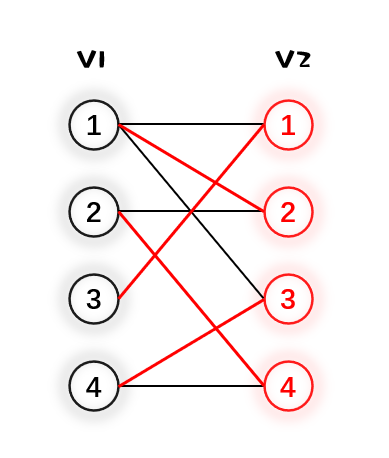
模板代码：
#include <iostream> #include <cstring> using namespace std; const int maxe = 5e4+5; const int maxn = 1005; struct Edge{ //链式前向星所需的结构体 int v; int next; Edge(int _v = 0, int _next = 0){ v = _v; next = _next; } }; Edge edge[maxe << 1]; //边数组 int head[maxn], cnt; //链式前向星所需变量 int n, m, e, ans; //n表示 v1 内点的数量，m表示 v2 内点的数量，e表示边的数量，ans表示最大匹配数 int vis[maxn]; //vis[i] 表示 v2 的 i 号点最后一次访问的时间戳 int pre[maxn]; //pre[i] 表示 v2 的 i 号点和 v1 内的哪个点匹配，默认为0表示无匹配 int tim; //此时时间戳 void addedge(int u, int v){ //链式前向星加边 edge[++cnt] = Edge(v, head[u]); head[u] = cnt; return; } int dfs(int u){ //dfs(i) 表示给 v1 的 i 号点找匹配点 for(int i = head[u]; ~i; i = edge[i].next){ //链式前向星遍历连接边 int v = edge[i].v; //v表示遍历边时找到的 $v2$ 内的点 if(vis[v] == tim) continue; //如果最后一次访问的时间戳和此时相同，就跳过 vis[v] = tim; //修改点v最后一次访问的时间戳 if(pre[v] == 0 || dfs(pre[v])){ //如果点v无匹配点，或者点v的匹配点（v1内的点）找到了新的匹配点 pre[v] = u; //点v和点u匹配 return 1; //为点u找到了匹配点，返回1 } } return 0; //点u没有找到匹配点，返回0 } int main(){ memset(head, -1, sizeof head); cin >> n >> m >> e; for(int i = 1; i <= e; i++){ int u, v; cin >> u >> v; addedge(u, v); } for(int i = 1; i <= n; i++){ //遍历v1内的点 tim++; //时间戳加一 if(dfs(i)) ans++; //给 v1 的 i号点找匹配点 } cout << ans; return 0; }
