学习:字符串----AC自动机
AC自动机是比较常用的一种多模式串匹配的算法,算法以Trie树为基础,以失配指针为重点。本篇基于KMP来讲解
暴力多模式串匹配
暴力多模式串匹配有好多方法,最基本的就是每个模式串都进行一次文本串匹配,复杂度为 $O(tnm)$,其中 $t$ 为模式串数量,$n, m$ 分别为每个模式串。其次就是每个模式串与文本串进行一次kmp,复杂度为 $O(t*(n+m))$,但是这种复杂度还是会超时。
有一个思路就是把所有的模式串合并为一棵Trie树,这样多个模式串就变为一棵模式树,这样就可以在模式树上寻找一棵从根节点到字符串结束标志节点的树枝,使得这棵树枝和文本串匹配。大致思路如下图所示:
假如文本串为“2225”
有三个模式串,分别为“2224”,“221”,“25”,那么先将三个模式串建成Trie树,然后如下图暴力匹配

这里只是提供暴力匹配的思路,不放出代码(和KMP一样有一个 $i$ 指针和 $j$ 指针,但是在树上很难做到 $i=i-j+1$)
在KMP中有一个 $Next$ 数组充当失配指针的作用,同理树上的每一个节点也可能会发生失配,故每个节点也存在一个失配指针指向其他节点,这就是AC自动机优化Trie树上匹配的方法。
Trie树上失配及失配(fail)指针
回想KMP算法,$Next[i]$ 含义主要是模式串 $P$ 的前缀子串的 $P[0],P[1],...,P[i-1]$ 的最长公共前后缀的长度。
同理,树上的节点失配也存在最长公共前后缀的情况,如下图所示(文本串为"2345")
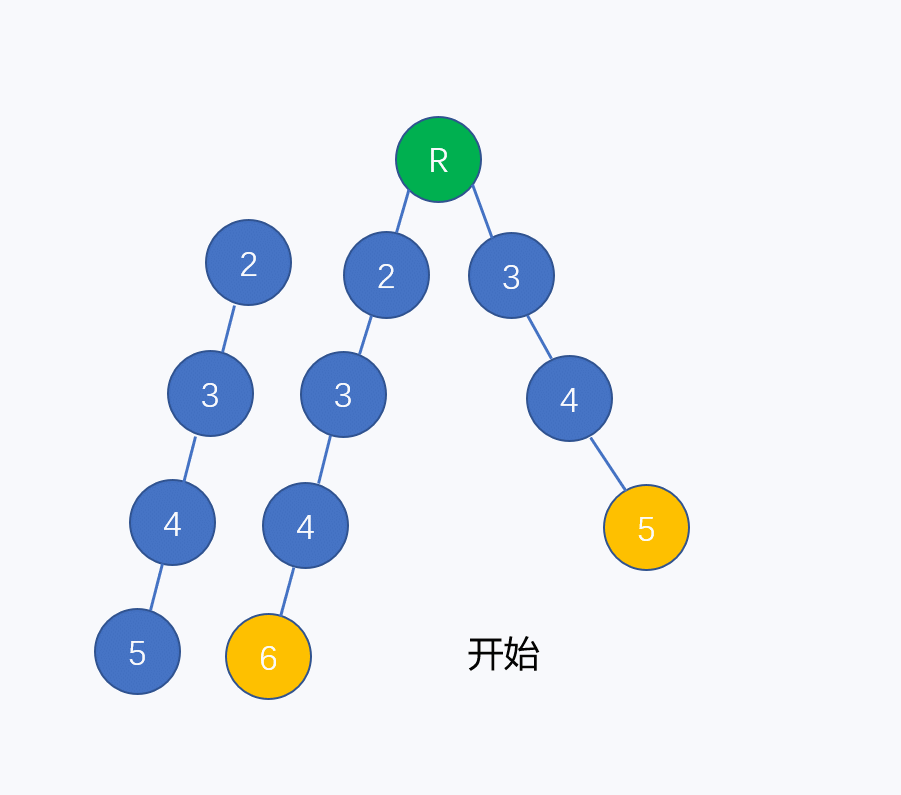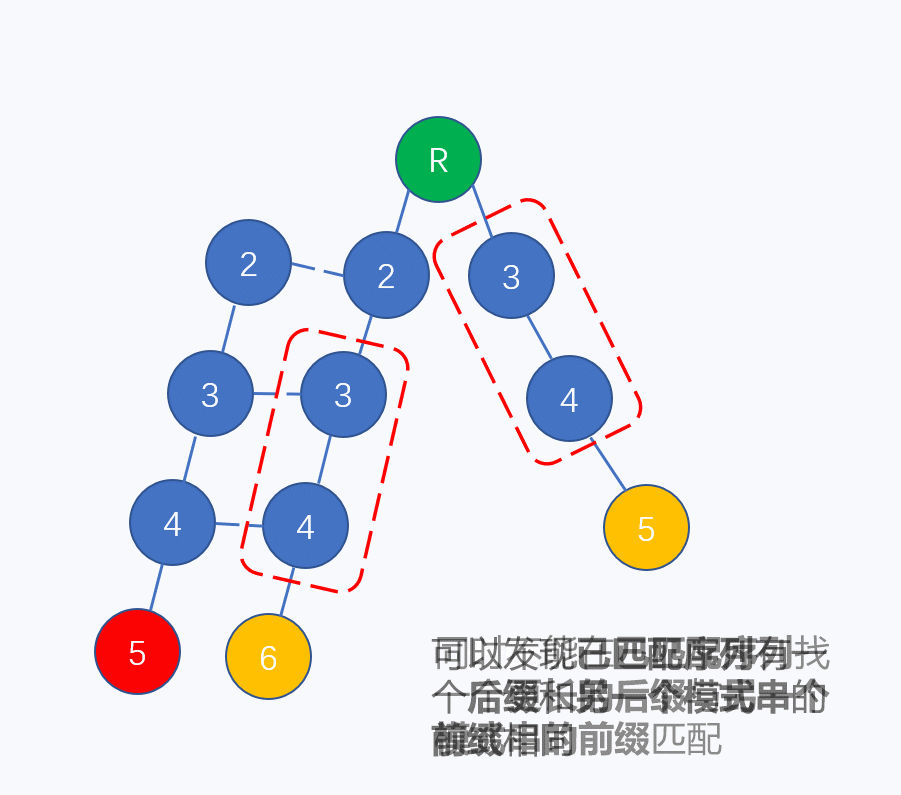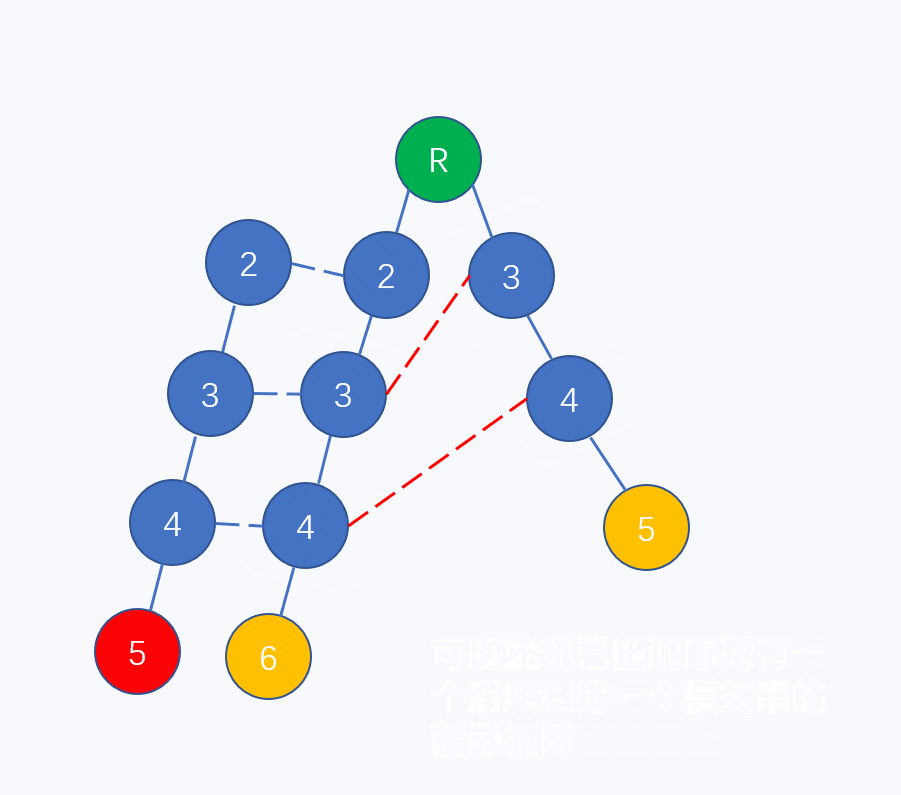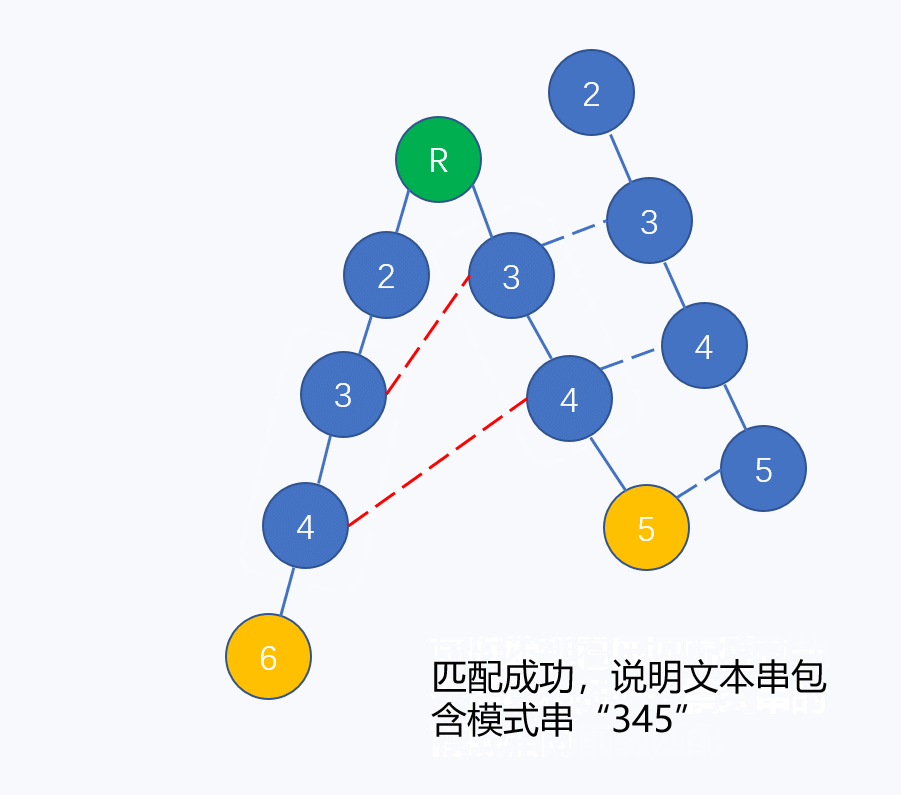
两条模式串形成一棵二叉树,在左子树4节点的子节点处失配,于是转移到右子树的4节点。所以认为左子树的4节点的失配指针指向右子树4,如下图:
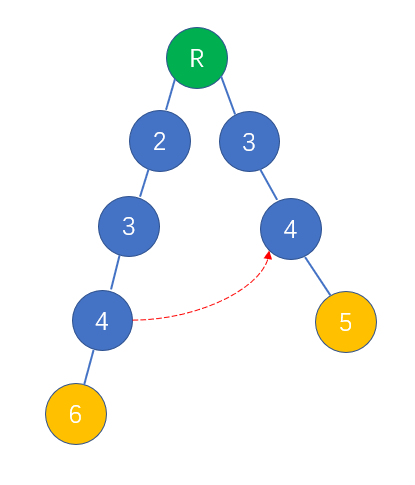
下面来探讨一下每个节点的失配指针($fail$ 指针)该指向哪个节点,模式树上面的节点分为3种:
1.根节点的 $fail$ 指针指向自己
根节点失配表示根节点下方没有匹配的字符节点,此时需要从文本串的下一个字符开始尝试匹配,所以根节点的 $fail$ 指针指向自己。
2.根节点的所有子节点的 $fail$ 指针指向根节点
这个类似于 KMP 算法中,$Next[0] = -1$,这里的根节点充当那个 $-1$ 的值,因为根节点不包含任何模式串内的字符,而根节点的所有子节点刚好为所有模式串第一个字符的集合。
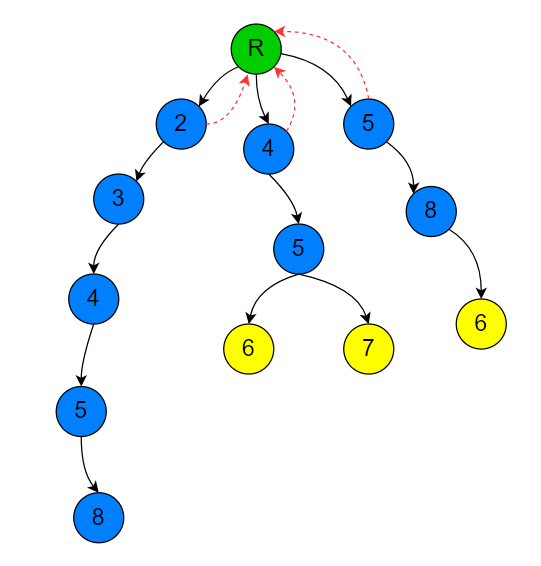
3.除上述节点以外的节点
假设当前节点 (P) 所表示的字符为 $c$ ,那么此节点 $fail$ 指针指向的节点为该节点 (P) 的父亲节点的 $fail$ 指针指向的节点的 $c$ 字符对应的子节点 (N)。
当然如果这个节点 (N) 不存在,那么就取该节点(P)的父亲节点的 $fail$ 指针指向的节点的 $fail$ 指针指向的节点(Z),然后再看此节点(Z)是否存在 $c$ 字符对应的子节点(V),如果存在,那么当前节点(P)的 $fail$ 指针指向该节点(V),否则就继续取(Z)节点的 $fail$ 指针指向的节点的操作,到根节点为止。(上面操作可以简述为爬 $fail$ 链)
如下面图所示,字符‘3’的 $fail$ 指针指向根节点,因为字符‘3’的父亲节点(字符'2'节点)的 $fail$ 指针指向的节点(根节点)没有表示字符‘3’的子节点,而根节点的 $fail$ 指针任然指向根节点。

又如下图所示,深度为3的字符‘4’节点的 $fail$ 指针指向的节点为深度为1的字符‘4’节点,因为深度为3的字符‘4’节点的父节点(字符'3'节点)的 $fail$ 指针指向的节点(根节点)刚好有一个表示字符‘4’的子节点(深度为1字符'4'节点)

最后还有下面情况,最下层字符‘8’节点的 $fail$ 指针指向深度为2的字符‘8’节点,因为最下层字符‘8’节点的父节点(深度为4的字符'5'节点)的 $fail$ 指针指向的节点(深度为2的字符'5'节点)没有代表字符‘8’的子节点,那就继续取 $fail$ 指针指向的节点(深度为1的字符'5'节点),可以发现该节点有一个代表字符‘8’的子节点(深度为2的字符'8'节点),所以指向该节点。
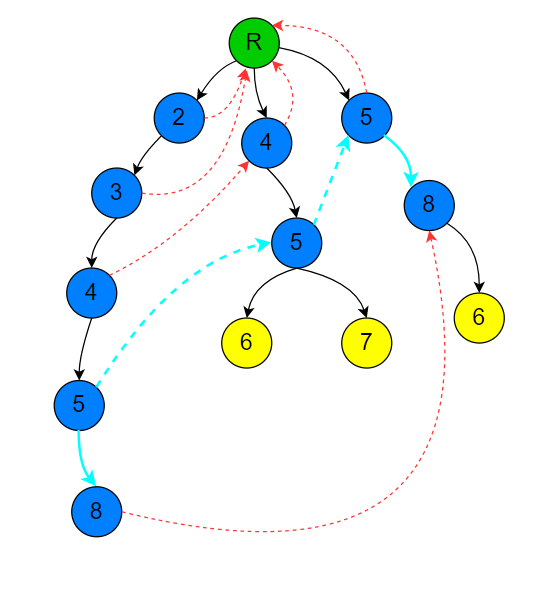
可以发现,要求当前节点的 $fail$ 指针指向的节点,我们要知道当前节点父节点的 $fail$ 指针指向的节点,所以算每个节点 $fail$ 指针指向的节点是一个宽搜的过程(先算第一层,再算第二层,再算第三层.....)。如下图所示(下图有一条黑色的虚线忘记改了,请把它看成一条黑色实线)
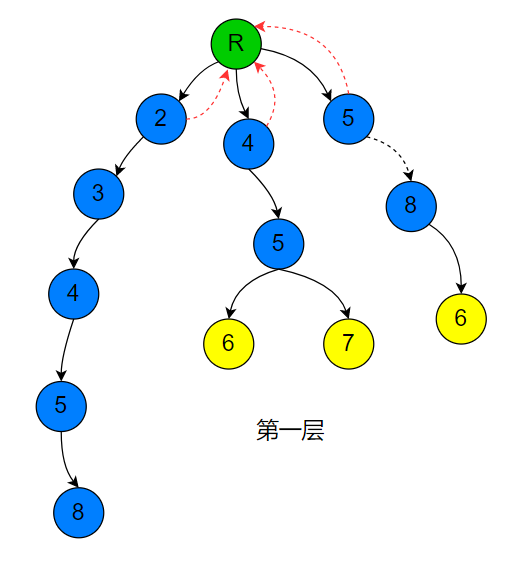



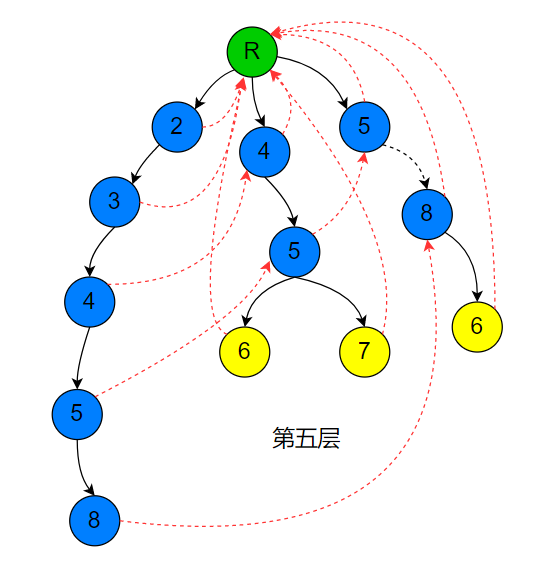
代码如下(本代码默认模式串和文本串只存在小写字母,所以根据实际要做出改变),下图红色部分存在一种优化,后面将介绍一下这种优化:
#include <iostream> #include <string> #include <queue> using namespace std; const int maxn = 1e6+5; int tree[maxn][27]; //tree[i][j] 表示编号为 i 的节点的第 j 个子节点(字符 ′a′+j)的编号 int cnt[maxn]; //cnt[i] 表示编号为 i 的节点的字符串结束标志的数量 int fail[maxn]; //fail[i] 表示编号为 i 的节点的fail指针指向的节点 queue<int> que; //宽搜求每个节点fail指针 int cnts = 0; //cnts 表示当前已使用的节点的数量 void insert(const string &str){ //trie树的插入操作 int root = 0; for(int i = 0; str[i] != '\0'; i++){ int now = str[i] - 'a'; //!!!!!! if(!tree[root][now]){ tree[root][now] = cnts++; } root = tree[root][now]; } cnt[root]++; return; } void getfail(){ for(int i = 0; i + 'a' <= 'z'; i++){ //先把根节点的子节点放入队列 if(tree[0][i]){ fail[tree[0][i]] = 0; que.push(tree[0][i]); } } while(que.size()){ int now = que.front(); //取出第一个节点 que.pop(); for(int i = 0; i + 'a' <= 'z'; i++){ //考虑当前节点的所有子节点 if(tree[now][i]){ //如果now节点的代表‘a’+i的子节点存在 fail[tree[now][i]] = tree[fail[now]][i]; //求得子节点fail指针节点的结论方法 que.push(tree[now][i]); //并把节点放入队列 } else{ //如果now节点的代表‘a’+i的子节点不存在 tree[now][i] = tree[fail[now]][i]; //可以认为now节点的代表‘a’+i的子节点就是now节点的fail指针的节点的代表‘a’+i的子节点 } } } return; }
Trie图优化Fail指针
可能存在下面这种Trie树

通过这种图可以画出部分 $fail$ 指针链
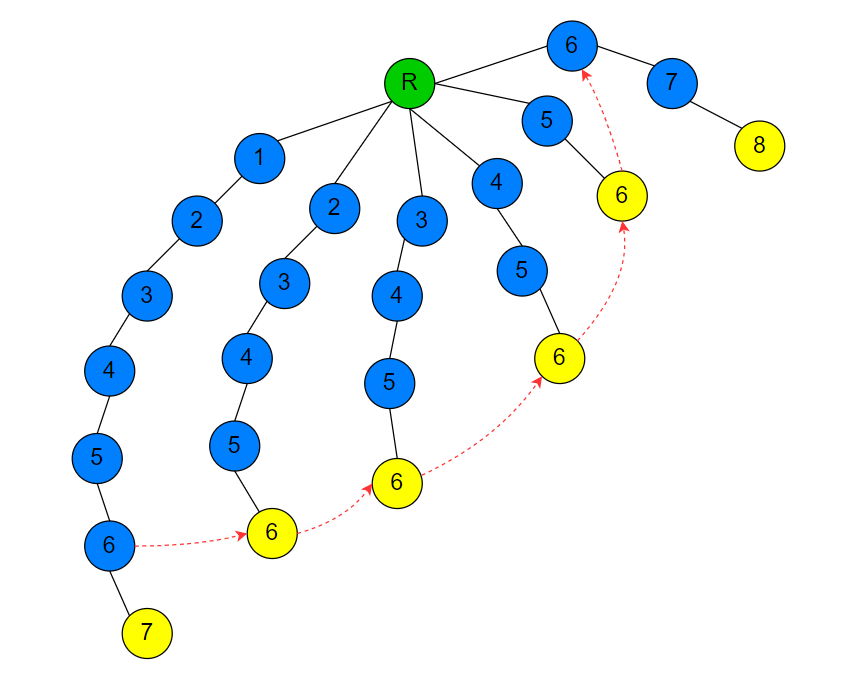
假设我们现在要求深度为7的字符‘7’节点的 $fail$ 指针指向哪个节点,理论上我们需要沿着该节点的父亲节点(深度为6的字符'6'节点)一直爬 $fail$ 链直到爬到深度为1的那个字符‘6’节点,最后找到深度为2的字符‘7’节点才是深度为7的字符‘7’节点的 $fail$ 指针指向的节点。

如果 $fail$ 链非常长,那么会使得算法复杂度退化,于是我们需要重点解决 $fail$ 链过长的问题
如果节点x它没有一个a字符的子节点,我们可以沿着节点x的 $fail$ 链找到第一个有a字符子节点的节点y,可以认为y的a字符子节点就是x的a字符子节点。
由于对于Trie树,都是用浅到深的考虑节点(宽搜),所以只需沿着 $fail$ 链爬一次左右就可以需找到满足条件的节点。
最后的子节点关系图(Trie图)如下(那个字符‘7’节点是这些字符‘6’节点共同的子节点)

那么寻找深度为7的字符‘7’节点 $fail$ 指针指向哪个节点,只需爬一次 $fail$ 链
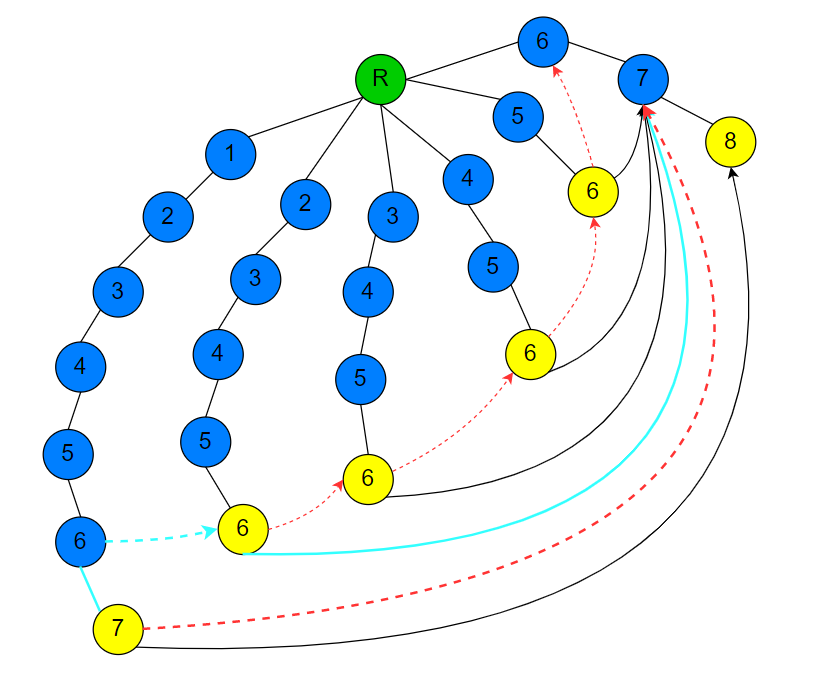
优化的代码部分:
void getfail(){ for(int i = 0; i + 'a' <= 'z'; i++){ //先把根节点的子节点放入队列 if(tree[0][i]){ fail[tree[0][i]] = 0; que.push(tree[0][i]); } } while(que.size()){ int now = que.front(); //取出第一个节点 que.pop(); for(int i = 0; i + 'a' <= 'z'; i++){ //考虑当前节点的所有子节点 if(tree[now][i]){ //如果now节点的代表‘a’+i的子节点存在 fail[tree[now][i]] = tree[fail[now]][i]; //求得子节点fail指针节点的结论方法 que.push(tree[now][i]); //并把节点放入队列 } else{ //如果now节点的代表‘a’+i的子节点不存在 tree[now][i] = tree[fail[now]][i]; //可以认为now节点的代表‘a’+i的子节点就是now节点的fail指针的节点的代表‘a’+i的子节点 } } } return; }
AC自动机
遍历文本串 $str$ 的每一个字符,假设此时遍历到了第 $i$ 个字符($str[i-1]$),于是就存在 $str[0],str[1],...,str[i-1]$ 这个文本串的前缀子串 $S$,同理这个前缀子串 $S$ 恰好有 $i$ 个后缀子串,判断每一个后缀子串是否为模式串的一个。但是有了 $fail$ 链和Trie图优化,复杂度就会变得很低。
代码如下:
int query(const string &str){ //str是文本串 int now = 0, ans = 0; for(int i = 0; str[i] != '\0'; i++){ now = tree[now][str[i]-'a']; //遍历每一个字符,相当于遍历文本串每一个前缀串 for(int j = now; j && cnt[j] != -1; j = fail[j]){ //以当前的字符节点爬fail链,相当于遍历当前前缀串的后准串,计算答案,爬到根节点为止 ans += cnt[j]; cnt[j] = -1; } } return ans; }
假设文本串为“12345”
模式串为“12”,“234”,“235”,“34”,“351”
上面的query代码过程图如下
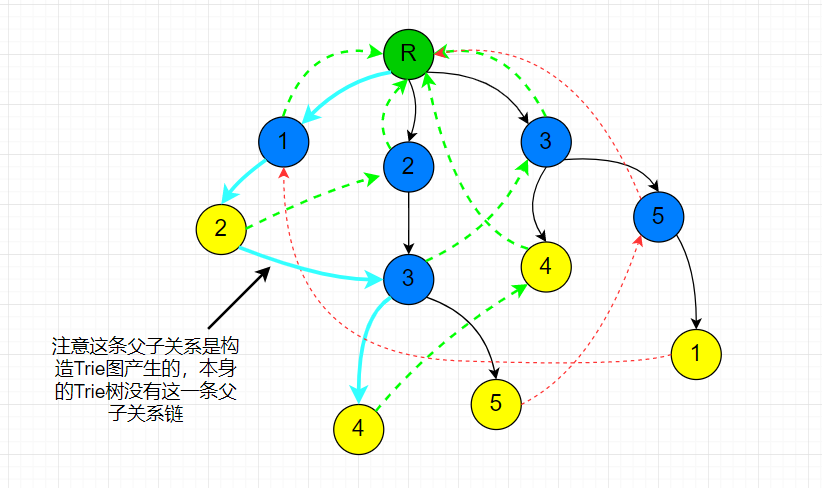
蓝色链是外层循环遍历文本串字符找子节点的路径(代码内 $now$ 值的变化),每一条绿色链(终点都是根节点)是内层循环爬 $fail$ 链计算答案的过程(如果通过 $fail$ 链爬到了字符串结束标志节点就加上对应值)


