学习：字符串----Trie树

Trie树，也叫字典树或者前缀树，是一类用空间换时间的数据结构，字典树同时也是AC自动机的重要前置算法，本身就可以降低字符串排序的复杂度。一般来说Trie树的题目，字符串的数量很多，但是每一条字符串很短，且字符串包含的字符属于给定的一个范围类（比如全为小写字母）

 

Trie树的建立

---

 

先来看看一条字符串的Trie树，对于字符串 "ACDABD" ，它的Trie树仅仅为一条单链，如图所示

 绿色节点表示Trie树的根节点，蓝色节点是Trie树的主要节点，橙色节点到根节点的所有蓝色/橙色节点的字符连接而成的字符串表示该Trie树所表示的一条字符串。

假入在上图的Trie树中再次插入一串字符串 "ACDBAD" ，那么原来的Trie树会变成

 

 

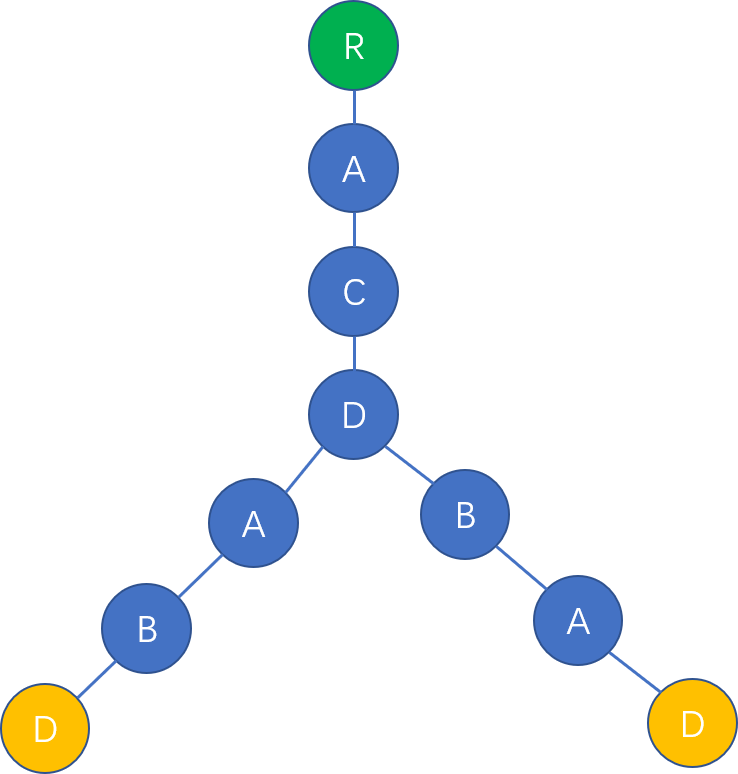
可以发现，两条字符串相同的前缀部分合并为同一条链串，而不同的部分分别成为一条链串，这也是字典树利用公共前缀降低时间开销的表示。

对于树上每一个节点，可以用一个结构体来表示

struct Trie{
    int exist;    //表示此节点是否为一条字符串的结束标志，exist的值表示字符串的数量
    Trie *child[30];    //指针
    Trie():exist(0){}
};

每一个节点都有一个指针数组来指向它的子节点，注意数组的大小和题目所说明的字符串内字符的种类数有关（假设所有字符串只包含大写字母）

 

那么建树的过程就是插入新字符串的过程，即遍历字符串每一个字符，然后再字典树上查找对应的子节点，如果能找到则继续往下进行步骤，不能找到，就创建新的子节点继续步骤。直到把字符串完全插入到树中为止。

int insert(Trie *t, const string &str){ //t为Trie树的根节点，str是需要插入的字符串
    Trie *root = t;
    for(int i = 0; i < str.size(); i++){    //遍历字符串每一个字符
        int place = str[i] - 'a';    //找到当前字符在数组中的下标
        if(root->child[place] != NULL)    //先判断当前字符的子节点是否存在
            root = root->child[place];     //存在就继续往下执行步骤
        else{
            root->child[place] = new Trie();    //不存在就创建新的节点
            root = root->child[place];
        }
        if(i == str.size() - 1){    //当当前root节点的深度和字符串长度一致，说明吧字符串已经插入到Trie树中了
            root->exist++;   //给当前节点的标记加一
            return root->exist;    //这里返回Trie树已经插入的str的数量
        }
    }
}

建树动画：

 

Trie树的性质总结：

1.根节点不包含任何字符，你可以将根节点理解为空字符，表示任何一条字符串的开始

2.从根节点到字符串结束标志节点（图中为橙色节点）所走过的节点的字符连接在一起的字符串，为该trie数所表示的一条字符串

3.在Trie数上查找一条字符串的复杂度为该字符串的长度，Trie不适合表示很长的字符串，这样会使树的高度变大

---

 

 

 

Trie树的优化

---

 

再探求Trie树的功能之前，先来讲一讲Trie的优化

在上面trie树的节点结构体中使用了指针数组，虽然可能不是所有的指针都指向了新的内存，但是指针本身就占有空间，所以需要从空间方面来优化，可以用STL内的map或者unordered_map来优化，这里要区别一下

 

map内部建了一颗红黑树，unordered_map建立了hash表，所以

1.节空间耗时间，使用map

struct Trie{
    int exist;
    map<int, Trie*> child;
    Trie():exist(0){}
};

2.节时间耗空间，使用unordered_map 

struct Trie{
    int exist;
    unordered_map<int, Trie*> child;
    Trie():exist(0){}
};

 

建树（插入字符串）的代码为

int insert(Trie *t, const string &str){
    Trie *root = t;
    for(int i = 0; i < str.size(); i++){    
        int place = str[i] - 'a';
        if(root->child.find(place) != root->child.end())    
            root = root->child[place]; 
        else{
            root->child[place] = new Trie();
            root = root->child[place];
        }
        if(i == str.size() - 1){
            root->exist++;
            return root->exist;
        }
    }
}

 

有些题目故意卡时间，有时候unordered_map能过而map过不了

---

 

 

 

Trie树的功能

---

 

1.字符串的排序

将所有字符串插入到Trie树中，然后中序遍历Trie树（假设字节点中，节点的顺序从‘a’到‘z’按顺序），每次遇到结束标志就记录当前字符串，得到的就是字符串排序后的结果，更适合于重新定义了26字母大小顺序后的字符串排序，复杂度为O(n)

 

2.寻找多个字符串的最长公共前缀

将所有字符串插入到Trie树中，只需遍历出深度最小的字符串结束标志节点即可。相反如果遍历出深度最深的字符串结束标志节点，则是找到了多个字符串中，两两字符串的公共前缀的最长前缀。

 

3.字符串检索

判断某个字符串是否出现过（Trie树的基本作用）

 

4.扩展：01字典树

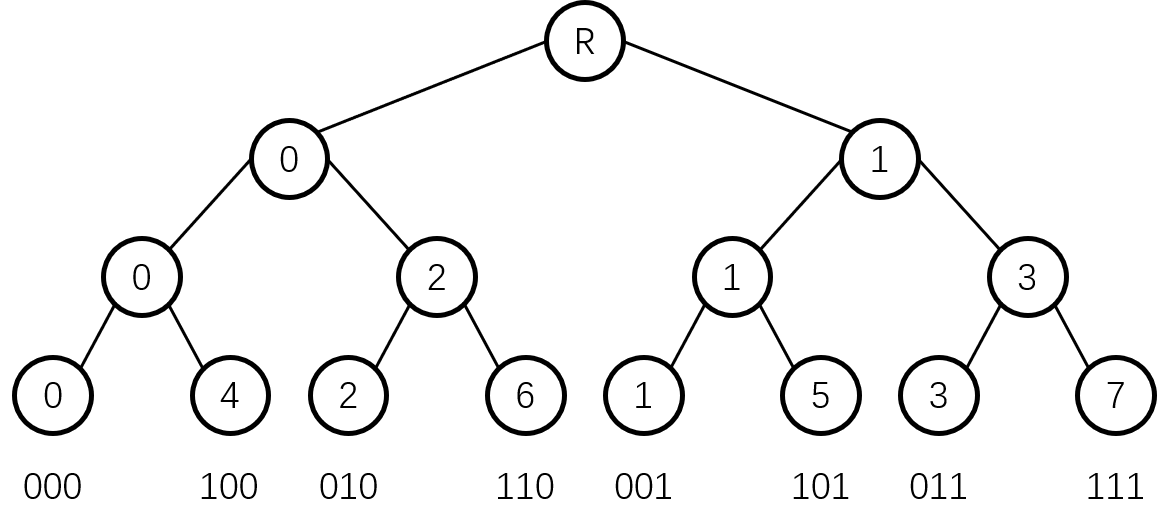
01字典树则是把插入字符改为了插入二进制字符（变成了二叉树），建树过程和建立普通Trie数一样，只不过01字典树可以表示很大的整数，例如深度为19的01字典树可以表示0~2²⁰-1的所有数。

 

5.多模式串匹配（AC自动机反面教材）

我们知道KMP算法可以解决单模式串匹配的问题，那么多模式串匹配可以利用Trie树来搞，把多模式串建立为一棵Trie树，以树上每一个节点为起点，然后暴力匹配文本串接下来的字符与树上当前起点以下的字符节点的字符。当然你也可以多次KMP，但是不管怎样都会TLE，解决多模式串匹配的算法可以用AC自动机。

---

 

 

 

基于数组的Trie树

---

 

有时候，有的Trie题目刻意会说所有的字符串长度之和小于 $n$ （假设 $n = 10^6$，且字符串只包含大写字母），既然知道了字符串总长度，就相当于知道了Trie树的节点数量，那么可以直接用数组表示整个Trie树

int tree[maxn][27];
int cnt[maxn];
int cnts = 0;

$tree[i][j]$ 表示编号为 $i$ 的节点的第 $j$ 个子节点（字符 $'a'+j$）的编号

$cnt[i]$ 表示编号为 $i$ 的节点的字符串结束标志的数量

$cnts$ 表示当前已使用的节点的数量

 

那么建树的代码为（注意 $tree$ 数组刚开始初始化为0，且编号为0的节点为根节点），AC自动机广泛使用了基于数组的Trie树

void insert(const string &str){
    int root = 0;
    for(int i = 0; str[i] != '\0'; i++){
        int now = str[i] - 'a';        
        if(!tree[root][now]){
            tree[root][now] = cnts++;
        }
        root = tree[root][now];
    }
    cnt[root]++;
    return;
}

---