最优化方法三:等式约束优化、不等式约束优化、拉格朗日乘子法证明、KKT条件
1 等式约束优化问题
等式约束问题如下:
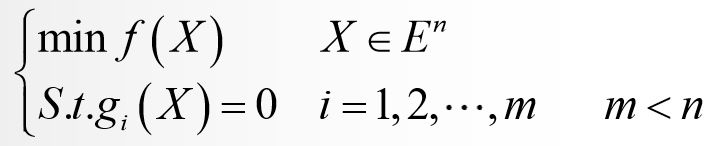
求解方法包括:消元法、拉格朗日乘子法。
1、消元法
通过等式约束条件消去一个变量,得到其他变量关于该变量的表达式代入目标函数,转化为无约束的极值求解问题,具体过程如下:
得到无约束的极值问题即可通过:一阶导数=0求驻点,Hession矩阵判定极值点。
2、拉格朗日乘子法
消元法大部分情况下很难适用,比如等式约束为高次耦合非线性,难以消去其中一个变量。拉格朗日乘子法适用于多维、高次、非线性约束方程。
拉格朗日乘子法(二维问题):

三个方程三个未知数,联立该方程即可求解最优的。
拉格朗日乘子法(多维问题):

得到的方程组,方程个数与未知变量个数相同,可以求解得出。
2 不等式约束优化问题与KKT条件
求解思路是对非线性约束条件引入松弛变量,转化为等式约束,二维问题如下:

注意,引入松弛变量是为了确保非负,这样满足约束函数小于等于0的条件。
多维问题如下:

引入松弛变量的作用是为了将不等式约束转化为等式约束,原理是:松弛变量是等高线负值,将不等式约束的取值面改为等式约束的取值曲线,但要满足不等式约束条件。
KKT条件:上述方法问题在于求解出来的解可能不满足原不等式约束条件,即解落于参数区域外。下面介绍通用的KKT条件:
KKT条件给出了不等式约束条件的优化问题,存在极值点的必要条件,即通过判定该条件来判定解是否存在,并利用KKT条件求解极值。必要条件如下:
KKT条件证明:

KKT条件应用说明:
3 拉格朗日乘子法证明
如果极值点存在,则极值点满足目标函数在约束曲线的切线方向方向导数为0,如下:
为什么?因为方向导数代表了曲面梯度在曲线切向方向的分量,梯度是曲面在该点上升的方向,如果曲面梯度与曲线切线向量乘积不为0,即梯度与曲线切线不垂直,则在该曲线上,沿着负梯度方向走,必然能找见更小的点。
同时易得:极值点满足约束函数再约束曲线切线方向的导数为0(二维函数),如下:
则对比上述两个方程切线矢量的系数可以得到:
4 KKT计算实例
对于如下非线性规划问题:







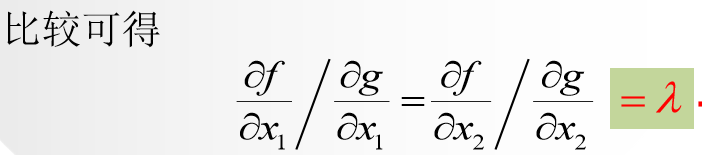

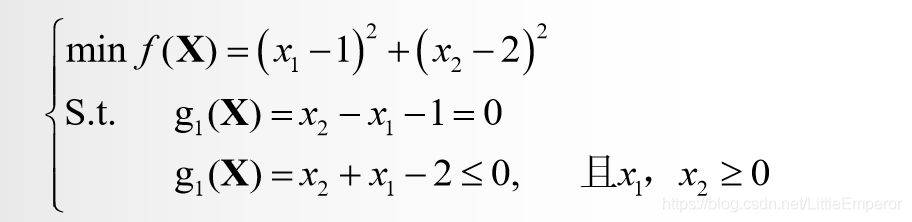

 浙公网安备 33010602011771号
浙公网安备 33010602011771号