先验概率，后验概率与似然函数

1.先验概率与后验概率
先验（A priori；又译：先天）在拉丁文中指“来自先前的东西”，或稍稍引申指“在经验之前”。近代西方传统中，认为先验指无需经验或先于经验获得的知识。它通常与后验知识相比较，后验意指“在经验之后”，需要经验。这一区分来自于中世纪逻辑所区分的两种论证，从原因到结果的论证称为“先验的”，而从结果到原因的论证称为“后验的”。

验前概率就是通常说的概率，验后概率是一种条件概率，但条件概率不一定是验后概率。贝叶斯公式是由验前概率求验后概率的公式。

先验概率是通过经验与以往的统计数据得来的。

后验概率是观察某事件已发生后，通过计算（贝叶斯公式）得到另一事件发生的概率。

举一个简单的例子：

一口袋里有3只红球、2只白球，采用不放回方式摸取，求：
⑴ 第一次摸到红球（记作A）的概率；
⑵ 第二次摸到红球（记作B）的概率；
⑶ 已知第二次摸到了红球，求第一次摸到的是红球的概率。
解：⑴ P(A)=3/5，这就是验前概率；
⑵ P(B)=P(A)P(B|A)+P(A逆)P(B|A逆)=3/5
⑶ P(A|B)=P(A)P(B|A)/P(B)=1/2，这就是验后概率。

还有一例：

玩英雄联盟占到中国总人口的60%，不玩英雄联盟的人数占到40%：

为了便于数学叙述，这里我们用变量X来表示取值情况，根据概率的定义以及加法原则，我们可以写出如下表达式：

P(X=玩lol)=0.6；P(X=不玩lol)=0.4，这个概率是统计得到的，即X的概率分布已知，我们称其为先验概率(prior probability)；

另外玩lol中80%是男性，20%是小姐姐,不玩lol中20%是男性，80%是小姐姐,这里我用离散变量Y表示性别取值，同时写出相应的条件概率分布：

P(Y=男性|X=玩lol)=0.8，P(Y=小姐姐|X=玩lol)=0.2

P(Y=男性|X=不玩lol)=0.2，P(Y=小姐姐|X=不玩lol)=0.8

那么我想问在已知玩家为男性的情况下，他是lol玩家的概率是多少：

依据贝叶斯准则可得：

P(X=玩lol|Y=男性)=P(Y=男性|X=玩lol)*P(X=玩lol)/

[ P(Y=男性|X=玩lol)*P(X=玩lol)+P(Y=男性|X=不玩lol)*P(X=不玩lol)]

最后算出的P(X=玩lol|Y=男性)称之为X的后验概率，即它获得是在观察到事件Y发生后得到的

 
2.似然函数
它是给定联合样本值下关于(未知)参数 的函数：

这里的小是指联合样本随机变量取到的值，即；

这里的是指未知参数，它属于参数空间；

这里的是一个密度函数，特别地，它表示(给定)下关于联合样本值的联合密度函数。

所以从定义上，似然函数和密度函数是完全不同的两个数学对象：前者是关于的函数，后者是关于的函数。所以这里的等号 理解为函数值形式的相等，而不是两个函数本身是同一函数(根据函数相等的定义，函数相等当且仅当定义域相等并且对应关系相等)。

似然函数和概率密度有两个主要的区别：

1.似然函数是参数的函数，不是随机变量的函数，而参数在一般情况下都是被认为常数的，不具有密度函数。

2.似然函数的积分并不等于1， 而概率密度的积分为1.

 

下面举一个例子：

有一个硬币，它有θ的概率会正面向上，有1-θ的概率反面向上。θ是存在的，但是你不知道它是多少。为了获得θ的值，你做了一个实验：将硬币抛10次，得到了一个正反序列：x=HHTTHTHHHH。

无论θ的值是多少，这个序列的概率值为 θ⋅θ⋅(1-θ)⋅(1-θ)⋅θ⋅(1-θ)⋅θ⋅θ⋅θ⋅θ = θ⁷ (1-θ)³，这就是它的似然函数。

 

 

 

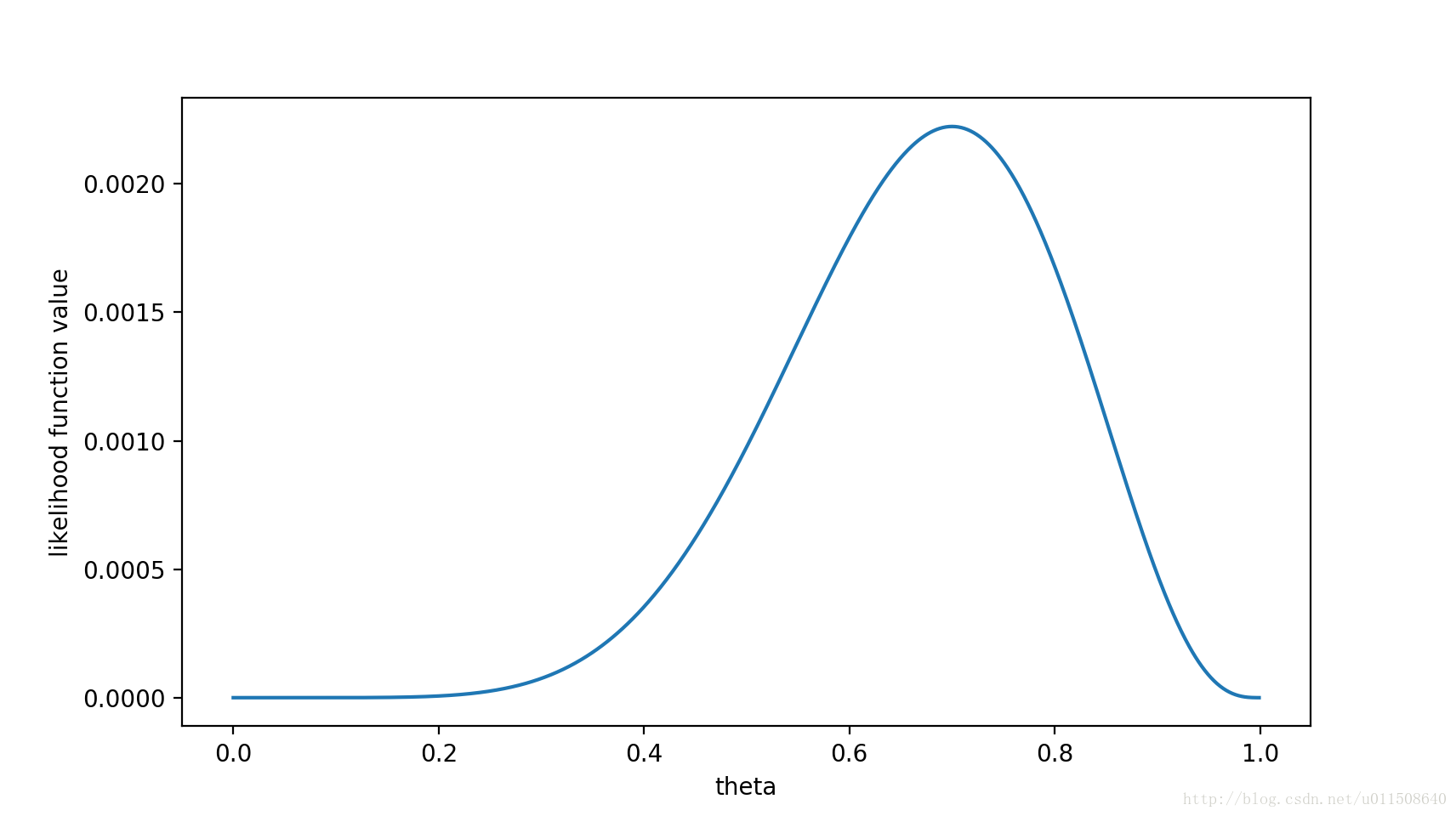
这个曲线就是θ的似然函数，通过了解在某一假设下，已知数据发生的可能性，来评价哪一个假设更接近θ的真实值。

如图所示，最有可能的假设是在θ=0.7的时候取到。但是，你无须得出最终的结论θ=0.7。事实上，根据贝叶斯法则，0.7是一个不太可能的取值（如果你知道几乎所有的硬币都是均质的，那么这个实验并没有提供足够的证据来说服你，它是均质的）。但是，0.7却是最大似然估计的取值。

因为这里仅仅试验了一次，得到的样本太少，所以最终求出的最大似然值偏差较大，如果经过多次试验，扩充样本空间，则最终求得的最大似然估计将接近真实值0.5。

 
原文链接：https://blog.csdn.net/a493823882/article/details/82657119