Delaunay和Voronoi
什么是Delaunay三角剖分?
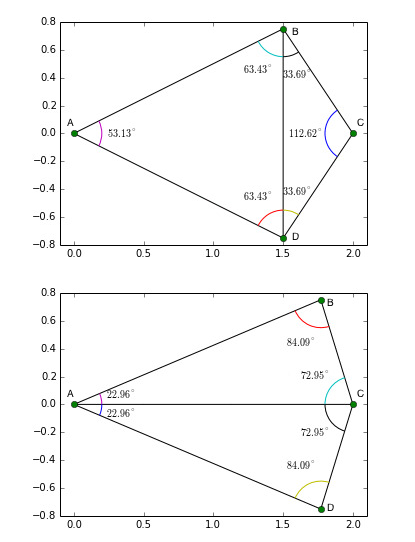
给定平面中的一组点,三角剖分指的是将平面细分为三角形,这些点为顶点。在图1中,我们在左侧图像上看到了一组地标,在中间图像上看到了三角剖分。一组点可以有许多可能的三角剖分,但是Delaunay三角剖分之所以突出是因为它具有一些不错的特性。在Delaunay三角剖分中,选择三角形时应确保没有点位于任何三角形的外接圆之内。图2.显示了四个点A,B,C和D的Delaunay三角剖分。在顶部图像中,要使该三角剖分成为有效的Delaunay三角剖分,C点应在三角形ABD外接圆的外部,而A点应在三角形ABD的外接圆的外部三角形BCD的外接圆。
Delaunay三角剖分的一个有趣特性是它不支持“瘦”三角形(即,一个大角度的三角形),即选择小角三角形,如下:
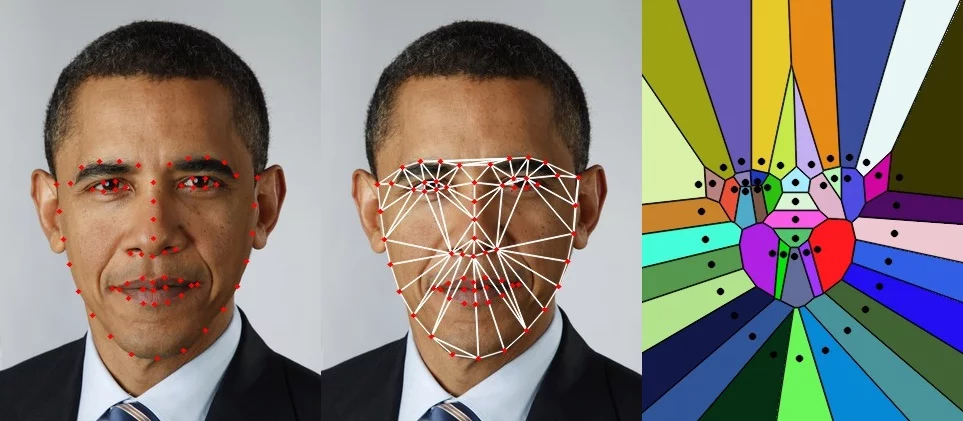
图1显示了在移动点时三角剖分如何变化以拾取“胖”三角形。在顶部图像中,点B和D在x = 1.5处具有x坐标,在底部图像中,它们向右移至x = 1.75。在顶部图像角度中,ABC和ABD的角度较大,而Delaunay三角剖分在B和D之间创建了一条边缘,将两个大角度分为较小的角度ABD,ADB,CDB和CBD。另一方面,在底部图像中,角度BCD太大,并且Delaunay三角剖分创建了边缘AC以划分大角度。
有很多算法可以找到一组点的Delaunay三角剖分。最明显(但不是最有效)的方法是从任何三角剖分开始,然后检查任何三角形的外接圆是否包含另一个点。如果是这样,则翻转边缘(如图1所示)并继续直到没有外接圆包含点的三角形。
关于Delaunay三角剖分的任何讨论都必须包括Voronoi图,因为一组点的Voronoi图是其Delaunay三角剖分的数学对偶。
什么是Voronoi图?
图2. Voronoi图
给定平面中的一组点,Voronoi图会划分空间,以使边界线与相邻点等距。图2.显示了根据显示为黑点的点计算的Voronoi图的示例。您会注意到,每条边界线都经过两个点的中心。如果将相邻的Voronoi地区中的点连接起来,则会得到Delaunay三角剖分!
Delaunay三角剖分和Voronoi图之间的联系不止一种。