虽然学深度学习有一段时间了,但是对于一些算法的具体实现还是模糊不清,用了很久也不是很了解。因此特意先对深度学习中的相关基础概念做一下总结。先看看前向传播算法(Forward propagation)与反向传播算法(Back propagation)。
1.前向传播
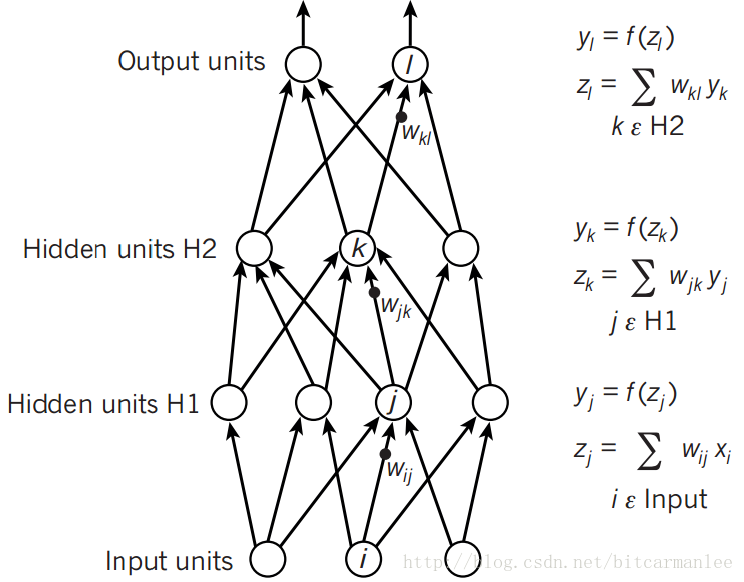
如图所示,这里讲得已经很清楚了,前向传播的思想比较简单。
举个例子,假设上一层结点i,j,k,…等一些结点与本层的结点w有连接,那么结点w的值怎么算呢?就是通过上一层的i,j,k等结点以及对应的连接权值进行加权和运算,最终结果再加上一个偏置项(图中为了简单省略了),最后在通过一个非线性函数(即激活函数),如ReLu,sigmoid等函数,最后得到的结果就是本层结点w的输出。
最终不断的通过这种方法一层层的运算,得到输出层结果。
对于前向传播来说,不管维度多高,其过程都可以用如下公式表示:
a2=σ(z2)=σ(a1∗W2+b2)a2=σ(z2)=σ(a1∗W2+b2)
其中,上标代表层数,星号表示卷积,b表示偏置项bias,σ表示激活函数。
2.反向传播算法(Back propagation)
BackPropagation算法是多层神经网络的训练中举足轻重的算法。简单的理解,它的确就是复合函数求偏导的链式法则,但其在实际运算中的意义比链式法则要大的多。要回答题主这个问题“如何直观的解释back propagation算法?” 需要先直观理解多层神经网络的训练。
机器学习可以看做是数理统计的一个应用,在数理统计中一个常见的任务就是拟合,也就是给定一些样本点,用合适的曲线揭示这些样本点随着自变量的变化关系.
深度学习同样也是为了这个目的,只不过此时,样本点不再限定为(x, y)点对,而可以是由向量、矩阵等等组成的广义点对(X,Y)。而此时,(X,Y)之间的关系也变得十分复杂,不太可能用一个简单函数表示。然而,人们发现可以用多层神经网络来表示这样的关系,而多层神经网络的本质就是一个多层复合的函数。下图来直观描绘一下这种复合关系。
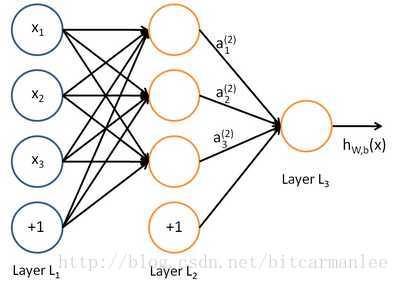
其对应的表达式如下:
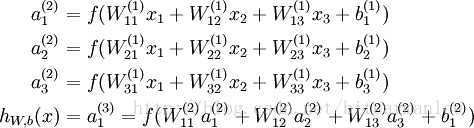
上面式中的Wij就是相邻两层神经元之间的权值,它们就是深度学习需要学习的参数,也就相当于直线拟合y=k*x+b中的待求参数k和b。
和直线拟合一样,深度学习的训练也有一个目标函数,这个目标函数定义了什么样的参数才算一组“好参数”,不过在机器学习中,一般是采用成本函数(cost function),然后,训练目标就是通过调整每一个权值Wij来使得cost达到最小。cost函数也可以看成是由所有待求权值Wij为自变量的复合函数,而且基本上是非凸的,即含有许多局部最小值。但实际中发现,采用我们常用的梯度下降法就可以有效的求解最小化cost函数的问题。
梯度下降法需要给定一个初始点,并求出该点的梯度向量,然后以负梯度方向为搜索方向,以一定的步长进行搜索,从而确定下一个迭代点,再计算该新的梯度方向,如此重复直到cost收敛。那么如何计算梯度呢?
假设我们把cost函数表示为H(W11,W12,⋯,Wij,⋯,Wmn)H(W11,W12,⋯,Wij,⋯,Wmn),那么它的梯度向量[2]就等于∇H=∂H∂W11e11+⋯+∂H∂Wmnemn∇H=∂H∂W11e11+⋯+∂H∂Wmnemn, 其中eijeij表示正交单位向量。为此,我们需求出cost函数H对每一个权值Wij的偏导数。而BP算法正是用来求解这种多层复合函数的所有变量的偏导数的利器。
我们以求e=(a+b)*(b+1)的偏导[3]为例。
它的复合关系画出图可以表示如下:
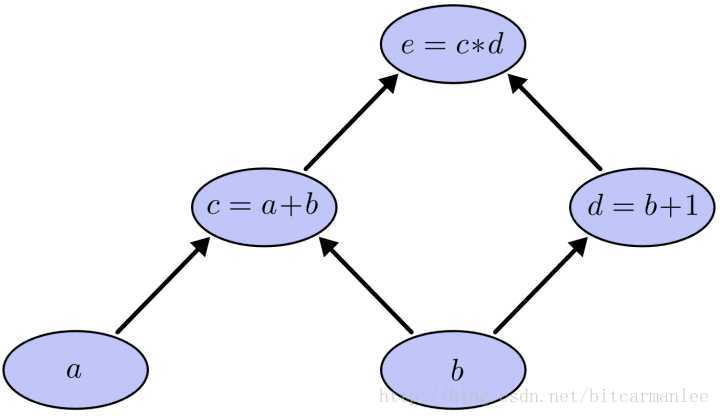
在图中,引入了中间变量c,d。
为了求出a=2, b=1时,e的梯度,我们可以先利用偏导数的定义求出不同层之间相邻节点的偏导关系,如下图所示。
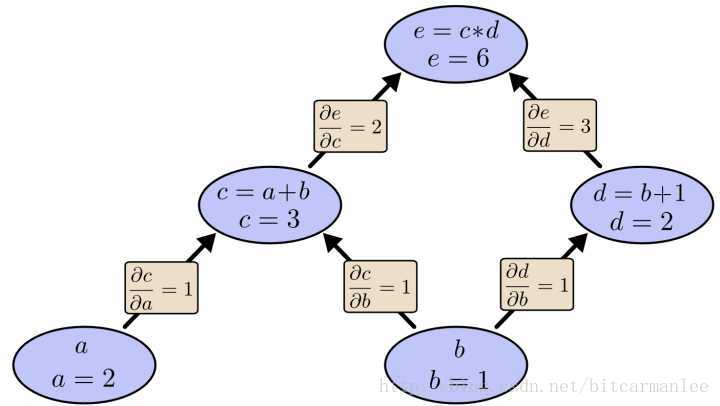
利用链式法则我们知道:
∂e∂a=∂e∂c⋅∂c∂a以及∂e∂b=∂e∂c⋅∂c∂b+∂e∂d⋅∂d∂b∂e∂a=∂e∂c⋅∂c∂a以及∂e∂b=∂e∂c⋅∂c∂b+∂e∂d⋅∂d∂b
链式法则在上图中的意义是什么呢?其实不难发现,∂e∂a∂e∂a的值等于从a到e的路径上的偏导值的乘积,而∂e∂b∂e∂b的值等于从b到e的路径1(b-c-e)上的偏导值的乘积加上路径2(b-d-e)上的偏导值的乘积。也就是说,对于上层节点p和下层节点q,要求得∂p∂q∂p∂q,需要找到从q节点到p节点的所有路径,并且对每条路径,求得该路径上的所有偏导数之乘积,然后将所有路径的 “乘积” 累加起来才能得到∂p∂q∂p∂q的值。
大家也许已经注意到,这样做是十分冗余的,因为很多路径被重复访问了。比如上图中,a-c-e和b-c-e就都走了路径c-e。对于权值动则数万的深度模型中的神经网络,这样的冗余所导致的计算量是相当大的。
同样是利用链式法则,BP算法则机智地避开了这种冗余,它对于每一个路径只访问一次就能求顶点对所有下层节点的偏导值。
正如反向传播(BP)算法的名字说的那样,BP算法是反向(自上往下)来寻找路径的。
从最上层的节点e开始,初始值为1,以层为单位进行处理。对于e的下一层的所有子节点,将1乘以e到某个节点路径上的偏导值,并将结果“堆放”在该子节点中。等e所在的层按照这样传播完毕后,第二层的每一个节点都“堆放”些值,然后我们针对每个节点,把它里面所有“堆放”的值求和,就得到了顶点e对该节点的偏导。然后将这些第二层的节点各自作为起始顶点,初始值设为顶点e对它们的偏导值,以”层”为单位重复上述传播过程,即可求出顶点e对每一层节点的偏导数。
以上图为例,节点c接受e发送的1*2并堆放起来,节点d接受e发送的1*3并堆放起来,至此第二层完毕,求出各节点总堆放量并继续向下一层发送。节点c向a发送2*1并对堆放起来,节点c向b发送2*1并堆放起来,节点d向b发送3*1并堆放起来,至此第三层完毕,节点a堆放起来的量为2,节点b堆放起来的量为2*1+3*1=5, 即顶点e对b的偏导数为5.
举个不太恰当的例子,如果把上图中的箭头表示欠钱的关系,即c→e表示e欠c的钱。以a, b为例,直接计算e对它们俩的偏导相当于a, b各自去讨薪。a向c讨薪,c说e欠我钱,你向他要。于是a又跨过c去找e。b先向c讨薪,同样又转向e,b又向d讨薪,再次转向e。可以看到,追款之路,充满艰辛,而且还有重复,即a, b 都从c转向e。
而BP算法就是主动还款。e把所欠之钱还给c,d。c,d收到钱,乐呵地把钱转发给了a,b,皆大欢喜。
3.反向传播具体计算过程推导
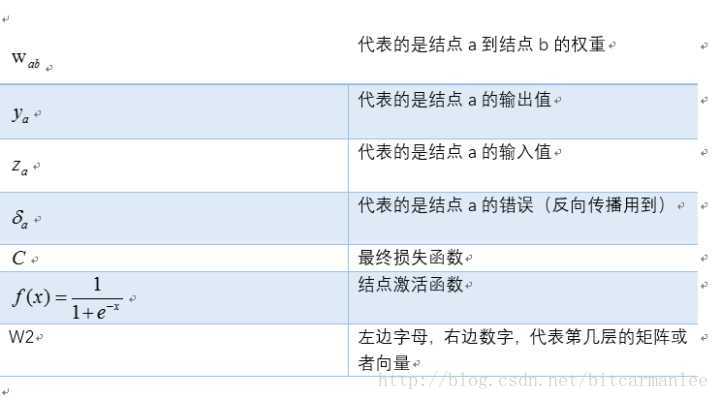
为了方便起见,这里我定义了三层网络,输入层(第0层),隐藏层(第1层),输出层(第二层)。并且每个结点没有偏置(有偏置原理完全一样),激活函数为sigmod函数(不同的激活函数,求导不同),符号说明如下:
对应网络如下:
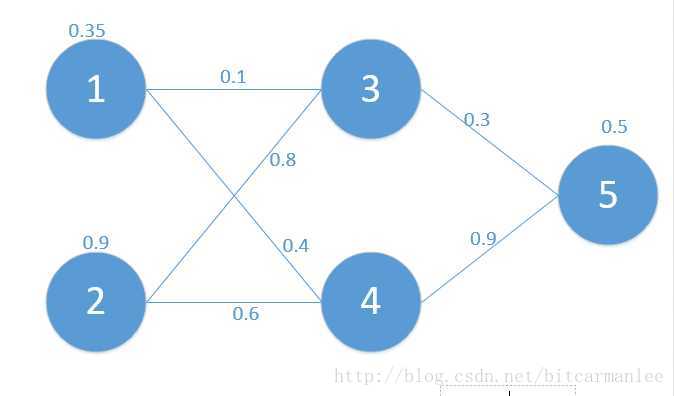
其中对应的矩阵表示如下
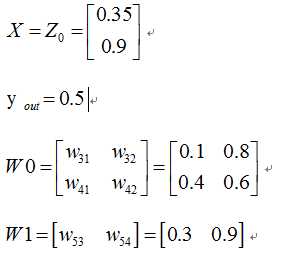
首先我们先走一遍正向传播,公式与相应的数据对应如下:

那么:
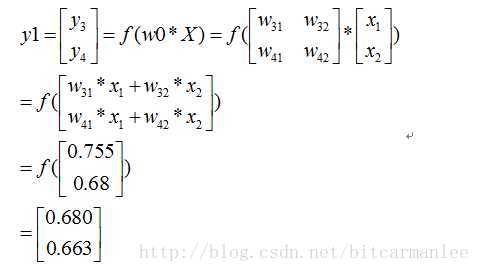
同理可以得到:
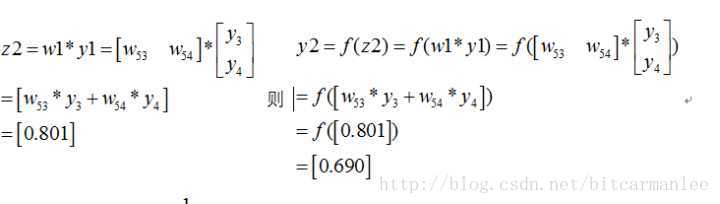
那么最终的损失为
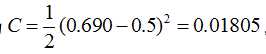
我们当然是希望这个值越小越好。这也是我们为什么要进行训练,调节参数,使得最终的损失最小。这就用到了我们的反向传播算法,实际上反向传播就是梯度下降法中链式法则的使用。
下面我们看如何反向传播
根据公式,我们有:
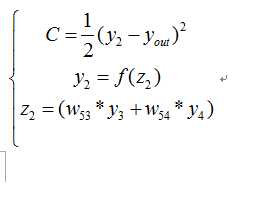
这个时候我们需要求出C对w的偏导,则根据链式法则有:
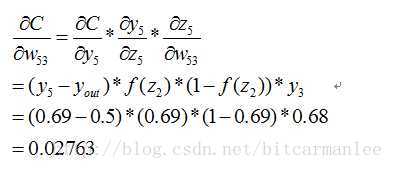
同理有:
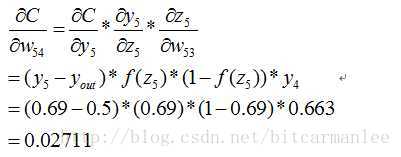
到此我们已经算出了最后一层的参数偏导了.我们继续往前面链式推导:
我们现在还需要求
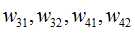
下面给出一个推导其它全都类似

同理可得其它几个式子:
则最终的结果为:

再按照这个权重参数进行一遍正向传播得出来的Error为0.165
而这个值比原来的0.19要小,则继续迭代,不断修正权值,使得代价函数越来越小,预测值不断逼近0.5.我迭代了100次的结果,Error为5.92944818e-07(已经很小了,说明预测值与真实值非常接近了),最后的权值为:

bp过程可能差不多就是这样了,可能此文需要你以前接触过bp算法,只是还有疑惑,一步步推导后,会有较深的理解。
上面的python代码实现如下:
#!/usr/bin/env python
#coding:utf-8
import numpy as np
def nonlin(x, deriv = False):
if(deriv == True):
return x * (1 - x)
return 1 / (1 + np.exp(-x))
X = np.array([[0.35], [0.9]])
y = np.array([[0.5]])
np.random.seed(1)
W0 = np.array([[0.1, 0.8], [0.4, 0.6]])
W1 = np.array([[0.3, 0.9]])
print 'original ', W0, '\n', W1
for j in xrange(100):
l0 = X
l1 = nonlin(np.dot(W0, l0))
l2 = nonlin(np.dot(W1, l1))
l2_error = y - l2
Error = 1 / 2.0 * (y-l2)**2
print 'Error:', Error
l2_delta = l2_error * nonlin(l2, deriv=True)
l1_error = l2_delta * W1 #back propagation
l1_delta = l1_error * nonlin(l1, deriv=True)
W1 += l2_delta * l1.T
W0 += l0.T.dot(l1_delta)
print W0, '\n', W1
参考文档:

