斐波那契数列--算法

斐波那契数列

斐波那契数列形式如下：

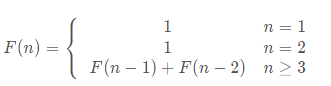
斐波那契数列的标准公式为：F(1)=1，F(2)=1, F(n)=F(n-1)+F(n-2)（n>=3，n∈N*）

方法一：递归法

int Fibonacci(int n){
    return n > 2 ? Fibonacci(n-1) + Fibonacci(n-2) : 1;
}

复杂度

• 时间复杂度：O (2 ^ n)
• 空间复杂度：O(1)

方法二：线性求法

int F[maxn];
int num; 	//num为我们需要求的最大的斐波那契数,num<N
void Fibonacci() {
    F[1] = F[2] = 1;
    for (int i = 3; i <= num; i++) {
        F[i] = F[i - 1] + F[i - 2];
    }
}

复杂度

• 时间复杂度：O (n)
• 空间复杂度：O(n)

优化后：

int Fibonacci(int n) {
    if (n == 1 || n == 2) return 1;
    int x = 0, y = 1, ans = 1;
    for (int i = 3; i <= n; i++) {
        x = ans;
        ans = ans + y;
        y = x;
    }
    return ans;
}

复杂度

• 时间复杂度：O (n)
• 空间复杂度：O(1)

方法三：公式法

斐波那契数列的通项公式为:

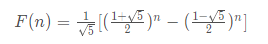
由于n增大时涉及大量浮点运算，会导致精度损失，因此无法通过浮点数计算斐波那契数列。

int Fibonacci(int n){
    return (pow((1 + sqrt(5)) / 2, n) - pow((1 - sqrt(5)) / 2, n)) / sqrt(5);
}

方法四：矩阵快速幂

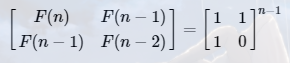
typedef long long ll;
const int Mod = 1e9 + 7;

struct Matrix {
    ll matrix[10][10];
};

int n;  //矩阵的阶数

Matrix mul(Matrix a, Matrix b) {
    Matrix res;
    memset(res.matrix, 0, sizeof res.matrix);
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            for (int k = 1; k <= n; k++) {   //对于新矩阵的(i,j)位置，即前行乘后列
                res.matrix[i][j] += (a.matrix[i][k] * b.matrix[k][j]) % Mod;
                res.matrix[i][j] %= Mod;
            }
    return res;
}

Matrix quick_pow(Matrix mx, ll x) {
    Matrix ans;   //快速幂我们初始化为1，那么这里就是矩阵的单位“1”，即单位矩阵
    memset(ans.matrix, 0, sizeof ans.matrix);
    for (int i = 1; i <= n; i++) ans.matrix[i][i] = 1;
    while (x) {
        if (x & 1) ans = mul(ans, mx);
        mx = mul(mx, mx);
        x >>= 1;
    }
    return ans;
}

ll solve(int m = 2, int x) {
    n = m;
    Matrix mx;  //特征矩阵及初始化
    mx.matrix[1][1] = 1, mx.matrix[1][2] = 1;
    mx.matrix[2][1] = 1, mx.matrix[2][2] = 0;
    ll ans = quick_pow(mx, x);
    return mx.matrix[2][1];
}

复杂度

• 时间复杂度：O (log n)
• 空间复杂度：O(1)

参考链接：

https://blog.csdn.net/qq_44691917/article/details/104101773
https://anguei.blog.luogu.org/solution-p1962
https://www.cnblogs.com/MMMMMMMW/p/12300262.html