[NOIp2015] 斗地主

题目类型：DFS+模拟

传送门：>Here<

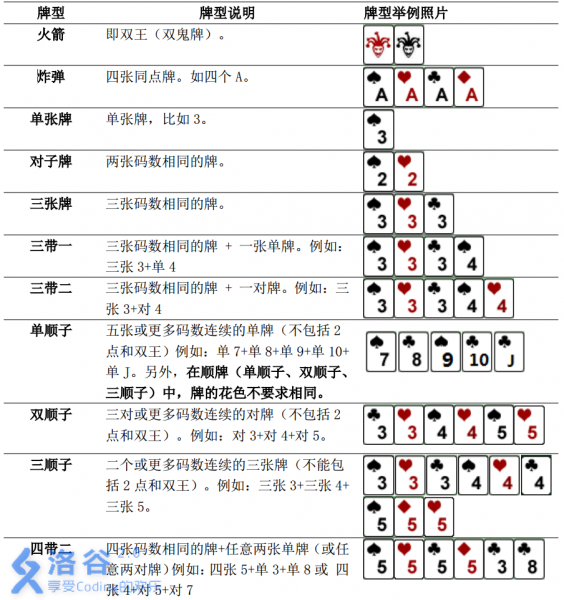
**题意：你有\(N\)张手牌，按照以下打法，最少打几次全部打完
**

解题思路

由于数据范围较小，明显就是爆搜。但是也不能真的“爆”搜，不然真的会爆……

考虑剪枝以及优化。很明显可以用一个类似记忆化的方法，当目前的次数已经超过已有的最小答案时即退出

那么是不是真的要搜索每一次用哪种方式打呢？肯定不是。

我们发现，题目要求我们最快打完，这与出牌的顺序毫无关系。如果我总是要出一个单顺子和四带二，那么先出哪个毫无关系。所以我们总是先考虑长的，先把长的出了，再出短的。因为这等价于先出短的再出长的。

我们发现除顺子以外的各种类型中，题目是帮你凑好的。也就是，只需要按照一个贪心策略取出就好了，并不需要\(DFS\)。四带两对里包括了炸弹和对子牌，因此如果可以出四带两对绝不出炸弹。因此我们肯定先出四带几再出炸弹。同样，我们肯定先出三带几再出三张……因此我们发现\(4,3,2,1\)的单排一定留到最后出。那么只需要考虑四带几和三带几怎么个顺序就好了。我们发现一个四带二等于一个三带二和一张单排，因此四带二肯定优于三带二，其他的同理。

于是我们得到贪心策略了。但是这里要注意，四带两张的要优先于四带一对（\(yy\)一下，出单牌的话两张需要两次，一对只需要一次）

因此我们只需要深搜顺子的出牌顺序，然后贪心剩下的牌。答案累积，打擂即可

Code

代码能力堪忧~

/*By DennyQi 2018*/
#include <cstdio>
#include <queue>
#include <cstring>
#include <algorithm>
#define  r  read()
using namespace std;
typedef long long ll;
const int MAXN = 10010;
const int MAXM = 20010;
const int INF = 1061109567;
inline int Max(const int a, const int b){ return (a > b) ? a : b; }
inline int Min(const int a, const int b){ return (a < b) ? a : b; }
inline int read(){
    int x = 0; int w = 1; register char c = getchar();
    for(; c ^ '-' && (c < '0' || c > '9'); c = getchar());
    if(c == '-') w = -1, c = getchar();
    for(; c >= '0' && c <= '9'; c = getchar()) x = (x<<3) + (x<<1) + c - '0'; return x * w;
}
int T,N,x,y,ans;
int num[20],cnt[20],tmp[20];
inline void Init(){
	ans = INF;
	memset(num, 0, sizeof(num));
	memset(cnt, 0, sizeof(cnt));
}
inline int CulculateSingle(){
	int res = 0;
	memset(tmp, 0, sizeof(tmp));
	for(int i = 3; i <= 16; ++i){
		++tmp[cnt[i]];
	}
	while(tmp[4] >= 1 && tmp[2] >= 2){
		tmp[4] -= 1, tmp[2] -= 2;
		++res;
	}
	while(tmp[4] >= 1 && tmp[1] >= 2){
		tmp[4] -= 1, tmp[1] -= 2;
		++res;
	}
	while(tmp[4] >= 1 && tmp[2] >= 1){
		tmp[4] -= 1, tmp[2] -= 1;
		++res;
	}
	while(tmp[3] >= 1 && tmp[2] >= 1){
		tmp[3] -= 1, tmp[2] -= 1;
		++res;
	}
	while(tmp[3] >= 1 && tmp[1] >= 1){
		tmp[3] -= 1, tmp[1] -= 1;
		++res;
	}
	while(tmp[4] >= 1){
		--tmp[4];
		++res;
	}
	while(tmp[3] >= 1){
		--tmp[3];
		++res;
	}
	while(tmp[2] >= 1){
		--tmp[2];
		++res;
	}
	while(tmp[1] >= 1){
		--tmp[1];
		++res;
	}
	return res;
}
void DFS(int step){
	if(step >= ans){
		return;
	}
	int tmp = CulculateSingle();
	ans = Min(ans, tmp + step);
	bool flg;
	for(int len = 2; len <= 12; ++len){
		for(int S = 3; S + len - 1 <= 14; ++S){
			flg = 1;
			for(int i = S; i < S + len; ++i){
				if(cnt[i] < 3){
					flg = 0;
					break;
				}
			}
			if(flg){
				for(int i = S; i < S + len; ++i){
					cnt[i] -= 3;
				}
				DFS(step+1);
				for(int i = S; i < S + len; ++i){
					cnt[i] += 3;
				}
			}
		}
	}
	for(int len = 3; len <= 12; ++len){
		for(int S = 3; S + len - 1 <= 14; ++S){
			flg = 1;
			for(int i = S; i < S + len; ++i){
				if(cnt[i] < 2){
					flg = 0;
					break;
				}
			}
			if(flg){
				for(int i = S; i < S + len; ++i){
					cnt[i] -= 2;
				}
				DFS(step+1);
				for(int i = S; i < S + len; ++i){
					cnt[i] += 2;
				}
			}
		}
	}
	for(int len = 5; len <= 12; ++len){
		for(int S = 3; S + len - 1 <= 14; ++S){
			flg = 1;
			for(int i = S; i < S + len; ++i){
				if(cnt[i] < 1){
					flg = 0;
					break;
				}
			}
			if(flg){
				for(int i = S; i < S + len; ++i){
					cnt[i] -= 1;
				}
				DFS(step+1);
				for(int i = S; i < S + len; ++i){
					cnt[i] += 1;
				}
			}
		}
	}
}
int main(){
	T = r, N = r;
	while(T--){
		Init();
		for(int i = 1; i <= N; ++i){
			x = r, y = r;
			if(x == 2) x = 15;
			else if(x == 1) x = 14;
			else if(x == 0) x = 16;
			++num[x];
		}
		for(int i = 3; i <= 16; ++i){
			cnt[i] = num[i];
		}
		DFS(0);
		printf("%d\n", ans);
	}
	return 0;
}