KMP与AC自动机
字符串匹配的基本方法就是,逐位移动模式串,检查当前位置是否匹配。似乎只有这样才能够不遗漏地检查所有可能匹配上的情况。容易发现,这样做的复杂度是\(O(nm)\)的。而事实是,我们可以做到比这更好。
KMP
我们来考虑我们基本做法中的一个环节。当我们把模式串放在某个位置从头开始匹配时,在某一位的时候突然发现失配了。那么我们认为我们应该做的是把模式串往后移动一位,并再次开始从头匹配。
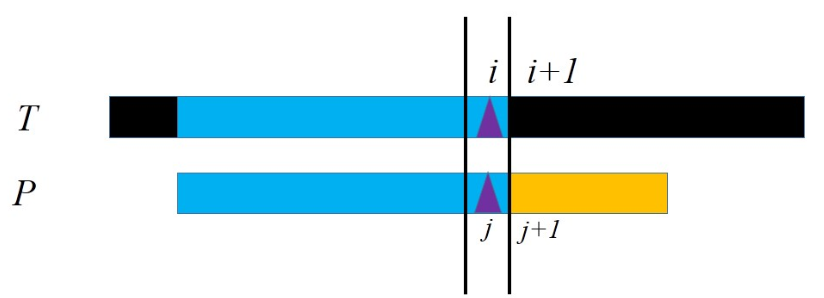
这里我们要意识到一个重要的事实:当我们说“模式串恰好在第\(i\)位失配”,隐含着“模式串的前\(i-1\)位全部匹配成功”。我们之所以在失配时把模式串往后移动一位,是因为我们不加思考地认为模式串在这个位置也有可能是全部匹配成功的。假如匹配成功,就意味着此时模式串和当前位置上的文本串完全相同。而由于刚才前\(i-1\)位匹配成功,当前位置上的文本串的前\(i-2\)位就是模式串的第\(2\)到第\(i-1\)位。因此模式串的\([1,i-2]\)和\([2,i-1]\)是完全相同的。我们完全绕开了文本串,发现“把模式串向后移动一位匹配成功”的一个必要条件是“模式串\([1,i-2]=[2,i-1]\)”。如果我们用某种方法预先知道了\([1,i-2] \neq [2,i-1]\),那么我们就知道把模式串向后移动一位一定是白费力气的,因此我们可以直接在失配时把模式串向后移动两位。而用完全相同的思路我们会发现,“向后移动两位之后匹配成功”的必要条件是“\([1,i-3]=[3,i-1]\)”……一般地,“向后移动\(k\)位之后匹配成功”的必要条件是“\([1,i-k-1]=[k+1,i-1]\)”。
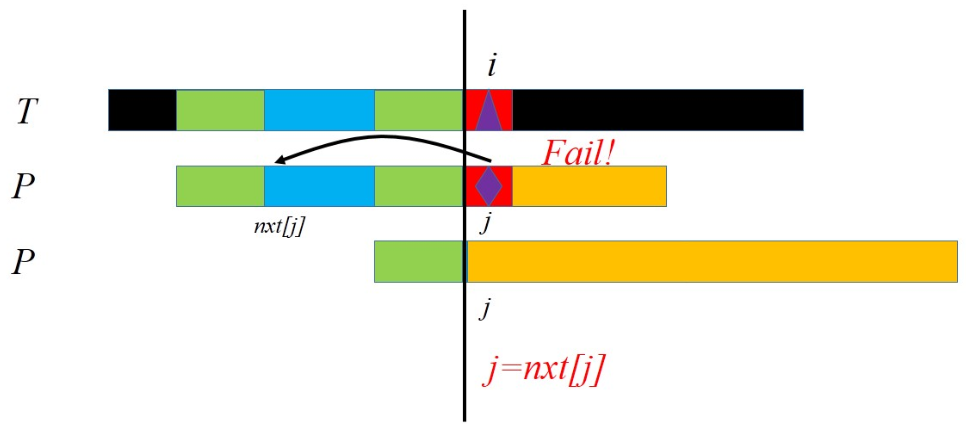
为了尽量地节省时间,我们只需要找到第一个满足\([1,i-k-1]=[k+1,i-1]\)的\(k\),然后把模式串向后移动\(k\)格继续进行匹配,这样的做法是完全不会破坏正确性的。这在数学上等价于,找到模式串\([1,i-1]\)中的最长相同前后缀(这是件很神奇的事,说明“匹配”和“前后缀”之间有很深的联系)。
假设我们已经求出了模式串的所有前缀的最长相同前后缀(把\([1,i]\)的最长相同前后缀记为\(pre[i]\)),那么在每一次在第\(i\)位失配的时候,有\(i-k-1=pre[i-1]\),解得\(k=i-1-pre[i-1]\)。因此只需要把模式串往后移动\(i-1-pre[i-1]\)格继续匹配就好了。我们假设有一个指针指向文本串地当前位,一个指针指向模式串的当前位。如果这两个指针对应的字符是匹配的,那么一同往右移一位;如果失配了,文本串的指针是不动的,模式串的指针往前“跳”了。而这个跳的距离等价于模式串向前移动的距离,这个移动距离总和不可能超过文本串的长度,因此总共跳的次数也不可能超过文本串的长度。因此我们发现,匹配的复杂度是线性的!
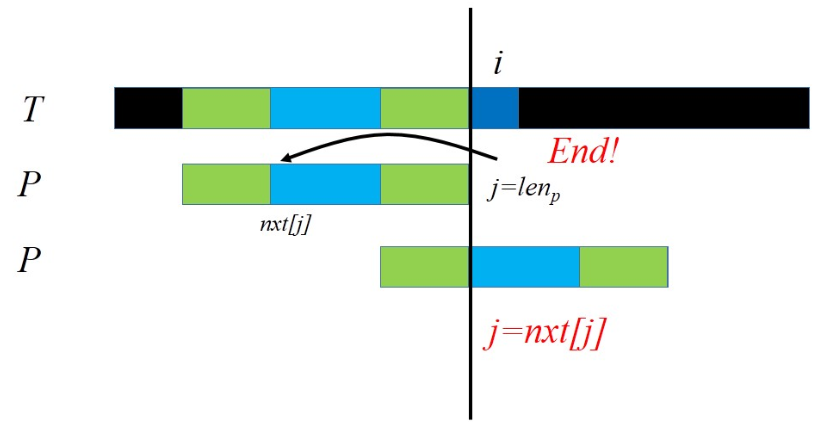
余下的问题是如何求解\(pre[i]\)。
我们可以这样求解:假设已经求出了\(pre[1..i-1]\),那么如果有\(s[i]=s[pre[i-1]+1]\),那么\(pre[i]\)一定可以等于\(pre[i-1]+1\)。而我们发现,不可能比这更大了,如果更大,就说明\([1..i-1]\)有大于\(pre[i-1]\)的相同前后缀,矛盾;如果不相等,那么我们找到\(pre[pre[i-1]]\),再次比较之后那一位,如果相等就可行,并可以用同样的方法证明不可能更大;如果依然不相等,那么继续找\(pre[pre[pre[i-1]]]\)。
以上的过程在操作上是容易的,但在复杂度的分析上却不容易。而我们发现,在寻找\(pre\)的过程中,我们可以做这样一个奇妙的等效——求解\(pre\)的问题可以转化为模式串自己和自己的匹配!为了找到\([1,i]\)的最长相同前后缀,可以数学上等价地转化为依次用模式串的\([1,k]\)去和模式串的\([i-k+1,i]\)匹配,找到最大的那个\(k\)。这等价于我们取两个完全相同的模式串\([1,i]\),第二个的第1位对准第一个的第2位开始,和“匹配文本串”完全相同的方法把他们互相匹配(由于\(pre[1..i-1]\)已经求出来了,这样做完全是可行的)。对于失配的处理也是完全相同的。直到我们找到第一个匹配的位置,也就求出了\(pre[i]\)。复杂度显然也是线性的。
#include <cstdio>
#include <cstring>
using namespace std;
int n,m,p,q;
char s[1000010],t[1000010];
int pre[1000010];
int main(){
// freopen("file.in","r",stdin);
scanf("%s%s",s,t);
n = strlen(s);
m = strlen(t);
pre[0] = 0;
int i = 1, j = 0;
while(i < m){
if(t[i] == t[j]){
pre[i] = j+1;
++i;
++j;
}else{
if(j == 0){
pre[i] = 0;
++i;
}
else j = pre[j-1];
}
}
while(p < n){
if(s[p] == t[q]){
++p;
++q;
if(q >= m){
printf("%d\n",p-m+1);
q = pre[q-1];
}
}else{
if(q == 0) ++p;
else q = pre[q-1];
}
}
for(int i = 0; i < m; ++i){
printf("%d ",pre[i]);
}
return 0;
}
AC自动机
如果模式串有多个,那么一旦失配,我们要在所有模式串中寻找前缀,使得它等于当前已经匹配部分的后缀。同样的,我们依然要求这个相同前后缀要尽可能长,这样才能保证不遗漏。
因此现在的问题是在多个模式串内,在每个模式串的每个前缀内寻找所有模式串中最长的相同前后缀。而这里我们的思想和KMP是一模一样的,因为我们同样可以继承上个节点的前后缀信息(或者理解为自己和自己匹配)。我们把所有模式串以前缀树(Trie树)的方式收集在一起,用fail指针代替pre数组即可(因为可能转移到别的模式串上)。这就是AC自动机。
有一个重要的优化可以避免我们在失配的时候不停地跳fail——在这里我们可以利用并查集中类似的路径压缩的思想,直接把失配的空儿子节点赋值为fail后应当到达的真实节点的位置,这样一继承我们就永远不会到达空节点了。这时AC自动机升级为了Trie图。
#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
int num,cnt,ans;
char s[1000010],t[1000010];
int ch[1000010][26],fail[1000010],ed[1000010];
queue <int> Q;
void get_fail(){
for(int i = 0; i < 26; ++i){
if(ch[0][i]){
Q.push(ch[0][i]);
}
}
while(!Q.empty()){
int u = Q.front();
Q.pop();
for(int i = 0; i < 26; ++i){
if(ch[u][i]){
Q.push(ch[u][i]);
fail[ch[u][i]] = ch[fail[u]][i];
}else{
ch[u][i] = ch[fail[u]][i];
}
}
}
}
int main(){
// freopen("file.in","r",stdin);
scanf("%d",&num);
for(int i = 1; i <= num; ++i){
scanf("%s",s);
int u = 0;
for(int j = 0, sz = strlen(s); j < sz; ++j){
if(cnt == 0 || ch[u][s[j]-'a'] == 0){
++cnt;
ch[u][s[j]-'a'] = cnt;
u = cnt;
}else{
u = ch[u][s[j]-'a'];
}
}
++ed[u];
}
get_fail();
scanf("%s",t);
int u = 0;
for(int i = 0, sz = strlen(t); i < sz; ++i){
u = ch[u][t[i]-'a'];
for(int v = u; v != 0; v = fail[v]){
if(!ed[v]) break;
ans += ed[v];
ed[v] = 0;
}
}
printf("%d\n",ans);
return 0;
}


