机器学习算法分类

是否在人类监督下进行训练（监督，无监督和强化学习）

在机器学习中，无监督学习就是聚类，事先不知道样本的类别，通过某种办法，把相似的样本放在一起归位一类；而监督型学习就是有训练样本，带有属性标签，也可以理解成样本有输入有输出。

所有的回归算法和分类算法都属于监督学习。回归和分类的算法区别在于输出变量的类型，定量输出称为回归，或者说是连续变量预测；定性输出称为分类，或者说是离散变量预测。

分类

• KNN
• 向量机SVC
• 朴素贝叶斯 
• 决策树DecisionTreeClassifier
• 随机森林RandomForestClassifier
• 逻辑回归--》softmax回归

回归

• 线性回归--》岭回归 lasso回归
• 向量机SVR
• 决策树DecisionTreeRegressor
• 随机森林回归RandomForestClassifier 

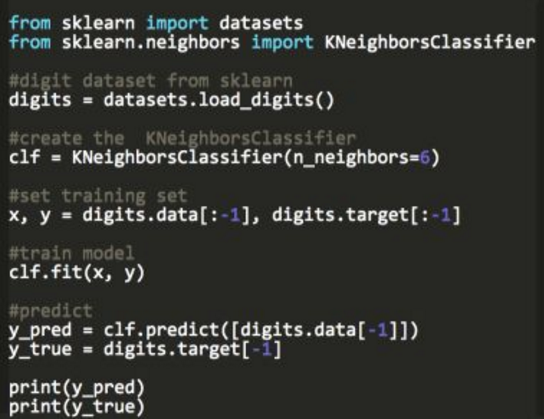
一. K-近邻算法（k-Nearest Neighbors，KNN）（分类）

K-近邻是一种分类算法，其思路是：如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别。

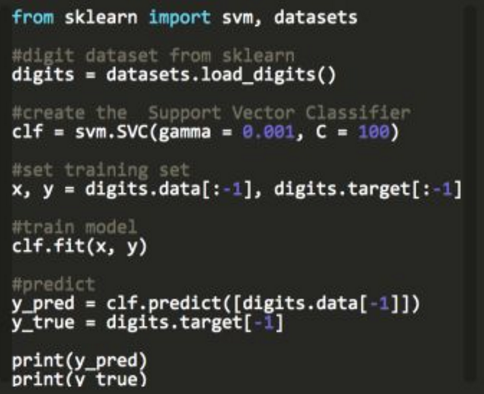
二．支持向量机SVM（可分类，可回归）

在 SVM 中，选择一个超平面，它能最好地将输入变量空间划分为不同的类，要么是 0，要么是 1。在 2 维情况下，可以将它看做一根线。

 

三．朴素贝叶斯（Naive Bayesian）（分类）

 

 

 

 

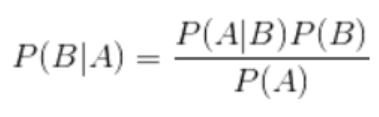
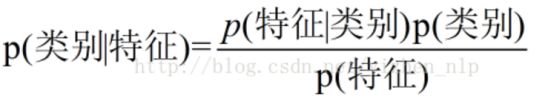
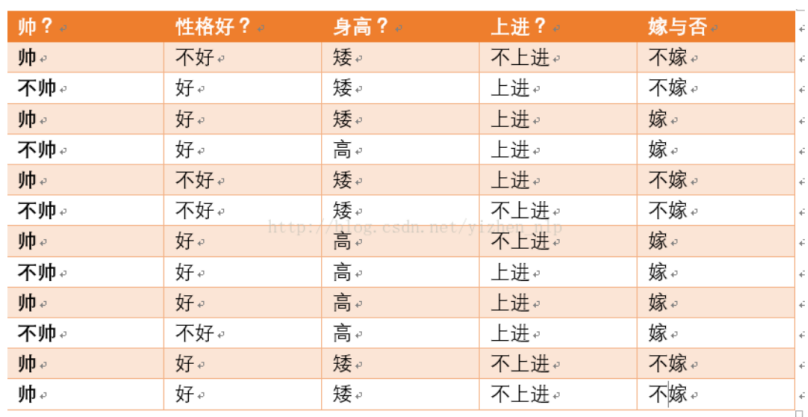
计算参考： https://blog.csdn.net/amds123/article/details/70173402

四. 线性回归算法 Linear Regression（回归）

线性回归就是根据已知数据集求一线性函数，使其尽可能拟合数据，让损失函数最小，常用的线性回归最优法有最小二乘法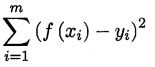

和梯度下降法。

线性回归又分为两种类型，即 简单线性回归（simple linear regression)，只有 1 个自变量；多变量回归（multiple regression)，至少两组以上自变量。

岭回归（也称为 Tikhonov 正则化）是线性回归的正则化版：在损失函数上直接加上一个正则项。

 

Lasso 回归（也称 Least Absolute Shrinkage，或者 Selection Operator Regression）是另一种正则化版的线性回归：就像岭回归那样，它也在损失函数上添加了一个正则化项，但是它使用权重向量的范数而不是权重向量范数平方的一半。

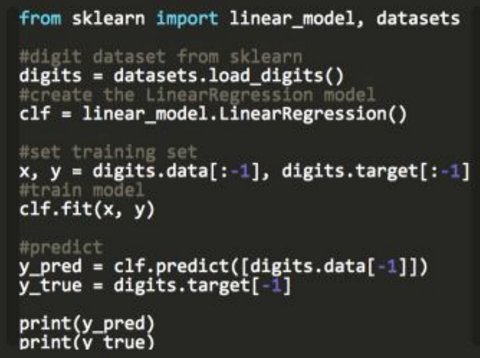
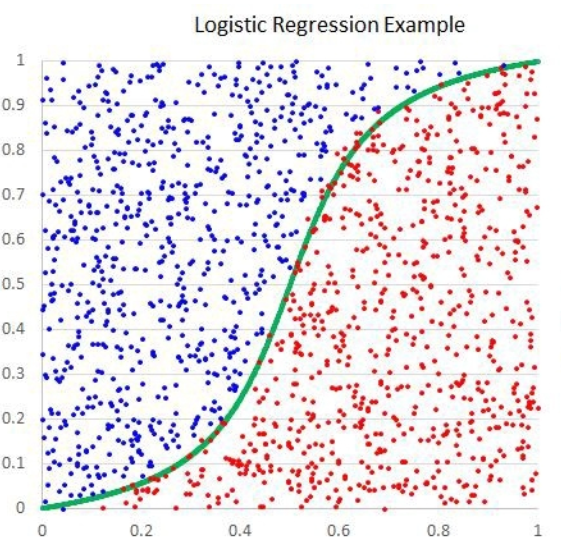
五. 逻辑回归（Logistic Regression）（分类）

逻辑回归是一种非线性回归模型，相比于线性回归，它多了一个sigmoid函数（或称为Logistic函数）。Sigmoid 函数（S 函数）是一种具有 S 形曲线，逻辑回归是一种分类算法，主要用于二分类问题。

逻辑回归算法一般用于需要明确输出的场景，如某些事件的发生（预测是否会发生降雨）。

Logistic 回归模型可以直接推广到多类别分类，不必组合和训练多个二分类器， 其称为 Softmax 回归或多类别 Logistic 回归。

 

六. 决策树（Decision Trees）（分类DecisionTreeClassifier、回归DecisionTreeRegressor）

决策树是一种基本的分类与回归方法，其模型就像一棵树来表示我们的决策过程，这棵树可以是二叉树（比如CART 只能是二叉树），也可以是多叉树（比如 ID3、C4.5 可以是多叉树或二叉树）。根节点包含整个样本集，每个叶节点都对应一个决策结果（注意，不同的叶节点可能对应同一个决策结果），每一个内部节点都对应一次决策过程或者说是一次属性测试。从根节点到每个叶节点的路径对应一个判定测试序列。

 

 

 

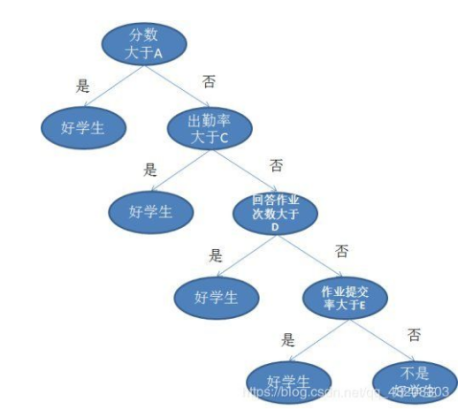
决策树算法：ID3、C4.5、CART

• ID3 使用信息增益作为选择特征的准则；信息增益 = 划分前熵 - 划分后熵（缺点：只能处理分类属性的数据，不能处理连续的数据；信息增益的缺点是倾向于选择取值较多的属性，在有些情况下这类属性可能不会提供太多有价值的信息。）
• C4.5 使用信息增益比作为选择特征的准则；信息增益比 = 信息增益 / 划分前熵 （C4.5 克服了 ID3 仅仅能够处理离散属性的问题，以及信息增益偏向选择取值较多特征的问题）
• CART 使用 Gini 指数作为选择特征的准则。（CART 生成的树必须是二叉树，Gini 指数最小化准则来选择特征进行划分）

剪枝

决策树算法很容易过拟合（overfitting），剪枝算法就是用来防止决策树过拟合，提高泛华性能的方法，剪枝分为预剪枝与后剪枝。

预剪枝是指在决策树的生成过程中，对每个节点在划分前先进行评估，若当前的划分不能带来泛化性能的提升，则停止划分，并将当前节点标记为叶节点。

后剪枝是指先从训练集生成一颗完整的决策树，然后自底向上对非叶节点进行考察，若将该节点对应的子树替换为叶节点，能带来泛化性能的提升，则将该子树替换为叶节点。

决策树总结

决策树算法主要包括三个部分：特征选择、树的生成、树的剪枝。常用算法有 ID3、C4.5、CART。

1、特征选择。特征选择的目的是选取能够对训练集分类的特征。特征选择的关键是准则：信息增益、信息增益比、Gini 指数；

2、决策树的生成。通常是利用信息增益最大、信息增益比最大、Gini 指数最小作为特征选择的准则。从根节点开始，递归的生成决策树。相当于是不断选取局部最优特征，或将训练集分割为基本能够正确分类的子集；

3、决策树的剪枝。决策树的剪枝是为了防止树的过拟合，增强其泛化能力。包括预剪枝和后剪枝。

 

七．随机森林（Random Forest）

 

决策树的集成叫做随机森林，是目前最强大的机器学习算法之一。（集成是合并了一组分类器的预测，要比单一预测器的效果好）

 

随机森林（Random Forest）是 Bagging 的一个变体。Ramdon Forest 在以决策树为基学习器构建 Bagging 集成的基础上，进一步在决策树的训练过程中引入随机属性选择.

相当于

集成学习

常见的集成算法：bagging、boosting、stacking、xgboost

一个非常简单去创建一个更好的分类器的方法就是去整合每一个分类器的预测，然后经过投票去预测分类。这种分类器就叫做硬投票分类器。

 

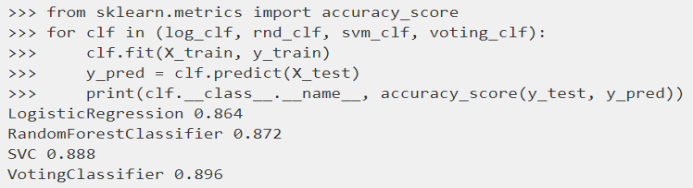
Bagging（bootstrap aggregating）

在Bagging方法中，利用bootstrap方法从整体数据集中采取有放回抽样得到N个数据集，在每个数据集上学习出一个模型，最后的预测结果利用N个模型的输出得到，具体地：分类问题采用N个模型预测投票的方式，回归问题采用N个模型预测平均的方式。

当我们通过一个使用决策树当做基分类器

Boosting（Adaboost、梯度提升）

Adaboost

使一个新的分类器去修正之前分类结果的方法就是对之前分类结果不对的训练实例多加关注。这导致新的预测因子越来越多地聚焦于这种情况。

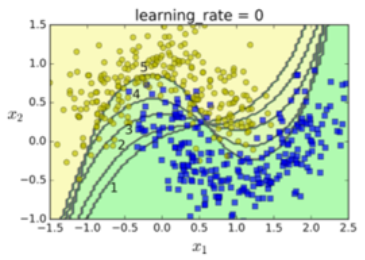
梯度提升

与 Adaboost 一样，梯度提升也是通过向集成中逐步增加分类器运行的，每一个分类器都修正之前的分类结果。然而，它并不像 Adaboost 那样每一次迭代都更改实例的权重，这个方法是去使用新的分类器去拟合前面分类器预测的残差 。

当我们通过一个使用决策树当做基分类器回归时。这被叫做梯度提升回归树（GBRT，Gradient Tree Boosting 或者 Gradient Boosted Regression Trees）

在回归问题中，这称为梯度提升回归树（GBRT），分类问题则称为梯度提升决策树（GBDT）。

 

Stacking

不使用琐碎的函数（如硬投票）来聚合集合中所有分类器的预测，我们为什么不训练一个模型来执行这个聚合？

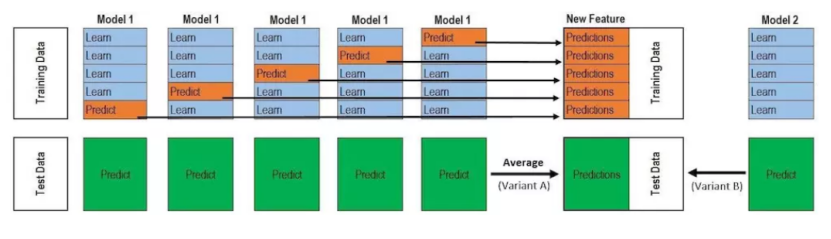
XGBoost

XGBoost 所应用的算法就是 GBDT（gradient boosting decision tree）的改进，既可以用于分类也可以用于回归问题中

全称：eXtreme Gradient Boosting

基础：GBDT

所属：boosting迭代型、树类算法。

适用范围：分类、回归

优点：速度快、效果好、能处理大规模数据、支持多种语言、支 持自定义损失函数等等。

 

根据个体学习器的生成方式，目前集成学习分为两大类：

个体学习器之间存在强依赖关系、必须串行生成的序列化方法。代表是 Boosting；

个体学习器之间不存在强依赖关系、可同时生成的并行化方法。代表是 Bagging 和随机森林（Random Forest）

GBDT 和随机森林区别（重点）

• GBDT 和随机森林的相同点：
• 都是由多棵树组成；
• 最终的结果都由多棵树共同决定。
• GBDT 和随机森林的不同点：
• 组成随机森林的可以是分类树、回归树；组成 GBDT 只能是回归树；
• 组成随机森林的树可以并行生成（Bagging）；GBDT 只能串行生成（Boosting）；这两种模型都用到了Bootstrap的思想。
• 对于最终的输出结果而言，随机森林使用多数投票或者简单平均；而 GBDT 则是将所有结果累加起来，或者加权累加起来；
• 随机森林对异常值不敏感，GBDT 对异常值非常敏感；
• 随机森林对训练集一视同仁权值一样，GBDT 是基于权值的弱分类器的集成；
• 随机森林通过减小模型的方差提高性能，GBDT 通过减少模型偏差提高性能。

逻辑回归和线性回归区别

 逻辑回归比线性回归好

两者两者都属于广义线性模型

线性回归优化目标函数用的最小二乘法，而逻辑回归用的最大似然估计。逻辑回归只是在线性回归的基础上，将加权和通过sigmoid函数，映射到0-1范围内空间。

线性回归在整个实数范围内进行预测，敏感度一致，而分类范围，需要在【0,1】。而逻辑回归就是一种减小预测范围，将预测值限定为【0,1】间的一种回归模型。

逻辑回归在z=0时，十分敏感，在z>>0或z<<0处，都不敏感，将预测值限定为（0,1）。逻辑回归的鲁棒性比线性回归要好。

LR和SVM的区别

Linear SVM和LR都是线性分类器

Linear SVM和LR都是判别模型

Linear SVM不直接依赖数据分布，分类平面不受一类点影响；LR则受所有数据点影响，如果数据不同类别处于极度不平衡的状态，一般需要先对数据做平衡处理。

Linear SVM依赖数据表达的距离测度，所以需要对数据先做标准化；LR不受其影响

Linear SVM依赖惩罚项的系数，实验中需要做交叉验证

Linear SVM和LR的执行都会受到异常值的影响，其敏感程度而言，谁更好很难下明确结论

Linear SVM和LR损失函数不同，LR为logloss,SVM为hinge loss.而SVM中的f(x) = max(0,1-x)称为hinge loss

 

本文参考：  scikit-learn官网

　　　　　《机器学习》 周志华

　　　　　《Sklearn 与 TensorFlow 机器学习实用指南》

　　　　　 知乎：机器学习面试干货精讲https://zhuanlan.zhihu.com/p/32877396　　utm_source=wechat_session&utm_medium=social&utm_oi=987374676359921664&from=singlemessage

　　　　     知乎：Machine Learning: 十大机器学习算法

https://zhuanlan.zhihu.com/p/33794257utm_source=wechat_session&utm_medium=social&s_s_i=p7XAeBT05ypHkJdaCw8JrAuEVQRCtQmfQGf2cNKMNb4%3D&s_r=1&from=singlemessage