机器学习之决策树
决策树和支持向量机一样, 决策树是一种多功能机器学习算法, 即可以执行分类任务也可以执行回归任务。
决策树也是随机森林的基本组成部分,而随机森林是当今最强大的机器学习算法之一。
一、决策树分类
1.1 实现决策树分类
from sklearn.datasets import load_iris from sklearn.tree import DecisionTreeClassifier iris = load_iris() X = iris["data"][:, 2:] # 仍旧只取长度和宽度两个特征 y = iris["target"] tree_clf = DecisionTreeClassifier(max_depth=2) tree_clf.fit(X, y)
DecisionTreeClassifier(class_weight=None, criterion='gini', max_depth=2, max_features=None, max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, min_samples_leaf=1, min_samples_split=2, min_weight_fraction_leaf=0.0, presort=False, random_state=None, splitter='best')
1.2 决策树的可视化
使用export_graphviz()方法,通过生成一个叫做iris_tree.dot的图形定义文件将一个训练好的决策树模型可视化
from sklearn.tree import export_graphviz #graphviz为图文的意思 export_graphviz( tree_clf, out_file="iris_tree.dot", feature_names=iris.feature_names[2:], class_names=iris.target_names, rounded=True, filled=True )
然后可以利用graphviz package [1] 中的dot命令行,将.dot文件转换成 PDF 或 PNG 等多种数据格式。例如,使用命令行将.dot文件转换成.png文件的命令如下:
[1] Graphviz是一款开源图形可视化软件包,http://www.graphviz.org/
决策树输出图像如下:

1.3解析,以1.2为例
1.首先一个决策树包含:一个根节点,一个决策树只包含一个根节点,即第一个节点若干个内部节点(一般的点),如上图中第二行右边的节点
若干个叶节点:产生决策结果的节点。如上图中彩色的节点,因为判断出了叶子类别因此是叶节点。
2.每个节点都有一个类别判断class的值。
3.因为在绿色节点中versicolor的样本数占到了48/54=90.74,所以该节点判定这个节点的类别是versicolor。
4.如果该类别的数量与该节点所有样本的数量一致,那么gini==0,gini代表的是纯度。他怎么算呢,以图中绿色节点为例:gini=1-(49/54)2-(5/49)2=0.168。
5.另外,因为设置的决策树深度为2,所以节点到第二层就停止了,如果设置为3的话,结果如下图

注:像决策树这种很容易解释的模型叫做白盒模型,而随机森林或者神经网络等就是黑盒模型了,它们能做很好的预测,但是你很难知道它们的预测过程。
- 输出概率。假设发现了一个花瓣长5cm,宽1.5cm的花朵,预测它分别是三种花的概率
tree_clf.predict_proba([[5, 1.5]]) #结果array([[0. , 0.90740741, 0.09259259]])
tree_clf.predict([[5, 1.5]]) #结果array([1])
二、决策树回归
2.1 CART训练算法
CART:全称Classification And Regression Tree分裂回归树
CART假设决策树是二叉树,内部结点特征的取值为“是”和“否”,左分支是取值为“是”的分支,右分支是取值为“否”的分支。这样的决策树等价于递归地二分每个特征,将输入空间即特征空间划分为有限个单元,并在这些单元上确定预测的概率分布,也就是在输入给定的条件下输出的条件概率分布。
CART算法由以下两步组成:
决策树生成:基于训练数据集生成决策树,生成的决策树要尽量大;
决策树剪枝:用验证数据集对已生成的树进行剪枝并选择最优子树,这时损失函数最小作为剪枝的标准。
CART决策树的生成就是递归地构建二叉决策树的过程。**CART决策树既可以用于分类也可以用于回归。**本文我们仅讨论用于分类的CART。对分类树而言,CART用Gini系数最小化准则来进行特征选择,生成二叉树。
2.2 剪枝
剪枝是决策树算法应对“过拟合”的主要手段。
剪枝分为预剪枝和后剪枝
预剪枝是:若当前节点的划分不能够带来泛化性能的提升,则不将该节点作为叶节点
后剪枝是:先生成一棵完整的决策树,然后自底向上考察,若将该节点设置为叶节点能够带来性能的提升,则将该节点替换为新的叶节点。
2.3 决策树回归
from sklearn.tree import DecisionTreeRegressor tree_reg = DecisionTreeRegressor(max_depth=2) tree_reg.fit(X, y)
DecisionTreeRegressor(criterion='mse', max_depth=2, max_features=None, max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, min_samples_leaf=1, min_samples_split=2, min_weight_fraction_leaf=0.0, presort=False, random_state=None, splitter='best')
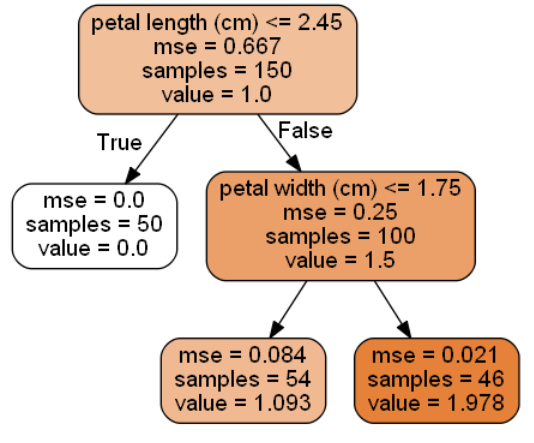
tree_reg.predict([[5, 1.5]])
#结果array([1.09259259])
可以看出,决策树回归预测的是一个具体的值。预测值为该叶节点相关的所有训练实例的平均目标值。通俗来讲,就是涉及到[5, 1.5]这个样本的判断,有一百多个预测器实例,不只是取最优的决策树,是所有的决策树,它们都对这个点有一个预测值,然后取平均值作为该点的预测值。
另外,CART算法在分类的时候:是以最小gini为目标找决策树
而在回归的时候,是以最小均方误差为目标找决策树
三、决策树的正则
随着决策树深度的增加,决策树很容易过拟合。所以就需要对模型的形状进行一定的限制,通过设置参数的方式来达到这个目的
min_samples_split(节点在被分裂之前必须具有的最小样本数)
min_samples_leaf(叶节点必须具有的最小样本数)
min_weight_fraction_leaf(和min_samples_leaf相同,但表示为加权总数的一小部分实例),max_leaf_nodes(叶节点的最大数量)和max_features(在每个节点被评估是否分裂的时候,具有的最大特征数量)。增加min_* hyperparameters或者减少max_* hyperparameters会使模型正则化。
一些其他算法的工作原理是在没有任何约束条件下训练决策树模型,让模型自由生长,然后再对不需要的节点进行剪枝。
四、决策树的缺点
决策树最大的缺点就是不稳定。随机森林可以通过多棵树的平均预测值限制这种不稳定性。



