机器学习之分类

本次使用的数据集是比较经典的mnist数据集。它有着 70000 张规格较小的手写数字图片，由美国的高中生和美国人口调查局的职员手写而成。这相当于机器学习当中的“Hello World”，人们无论什么时候提出一个新的分类算法，都想知道该算法在这个数据集上的表现如何。机器学习的初学者迟早也会处理 MNIST 这个数据集。接下来就是进行数据集的读取工作。

加载数据

机器学习的初学者迟早会接触Minist这个数据集，sklearn提供很多辅助函数用于下载流行的数据集

fetch_mldata出错修改方式

下载文件https://github.com/amplab/datascience-sp14/raw/master/lab7/mldata/mnist-original.mat
创建一个文件夹：datasets或mldata,将下载好的mnist-original.mat文件放在这个文件夹之中。
fetch_mldata('MNIST original', data_home="datasets")，data_home参数即为从本地导入数据的地址。

from sklearn.datasets import fetch_mldata

mnist = fetch_mldata('MNIST original', data_home="sample_data")
mnist

X, y = mnist["data"], mnist["target"]
print(X.shape)
print(y.shape)

可知，有70000个样本（图片），每个样本有784个特征值。这是因为每个图片都是28乘28个像素点的图片，每个像素点的值介于0-255之间。
可以通过Matplotlib的imshow函数展示出来

%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt

some_digit = X[36000]
some_digit_image = some_digit.reshape(28,28)
plt.imshow(some_digit_image, cmap = matplotlib.cm.binary, interpolation="nearest")
plt.axis("off")
plt.show()
y[36000]

创建数据集

这里要备注一下：为什么用这种切分数据集的方式呢。首先我们要知道这种方法是存在的且合理的。

首先我们要知道切分数据集的目的在于：评估泛化误差（就是用于预测误差）

其次要知道切分数据集的方法有很多种

留出法：就是这种方法，直接将数据且分为两个互斥子集

交叉验证法：将数据集分成k个互斥子集，然后每个子集作为测试集，其它子集的并集作为训练集进行测试然后取平均值

自助法：即常用的随机取数的方法

X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]

import numpy as np
shuffle_index = np.random.permutation(60000)
X_train, y_train = X_train[shuffle_index], y_train[shuffle_index]

训练一个二分类器

因为数据比较好，跳过了查找关联、数据清洗阶段。直接进行模型选择和评估。

先训练一个简单的，只识别数字“9”，修改样本集

y_train_5 = (y_train == 5)
y_test_5 = (y_test == 5)
print(y_train_5)

[False False  True ... False False  True]

使用决策树

from sklearn.linear_model import SGDClassifier

sgd_clf = SGDClassifier(random_state=42)
sgd_clf.fit(X_train, y_train_5)

sgd_clf.predict([some_digit]) # some_digit = X[36000]
# 这里加中括号的原因是：预测的数组X，要传入类array格式的数据，可以使numpy格式，也可以是list格式。
# 应该是一行代表一个样本。而如果直接传入some_digit格式的话，它只是一个样本，默认会把它的每一行作为一个样本，而实际上那只是一个样本中的一行而已。
# 最后预测为True，可见对于这一个样本预测的结果是正确的

array([ True])

评估性能

评估分类器比评估回归器更加玄学，本节会深入讲解

1.使用交叉验证评估性能

自己简写cross_val_score函数

StratifiedKFol类:分层k折交叉验证器，主要函数为split(),可以返回所有遍历的测试集和训练集的索引

from sklearn.model_selection import StratifiedKFold
from sklearn.base import clone 

skfolds = StratifiedKFold(n_splits=3, random_state=42)
for train_index, test_index in skfolds.split(X_train, y_train_5):
  clone_clf = clone(sgd_clf)
  X_train_fold = X_train[train_index]
  y_train_fold = (y_train_5[train_index])
  X_test_fold = X_test[test_index]
  y_test_fold = (y_test_5[test_index])

  clone_clf.fit(X_train_fold, y_train_fold)
  y_pred = clone_clf.pridict(X_test_fold)
  n_correct = sum(y_pred == y_test_5)
  print(n_correct/len(y_pred))

让我们使用 cross_val_score() 函数来评估 SGDClassifier 模型，同时使用 K 折交叉验证，此处让 k=3 。记住：K 折交叉验证意味着把训练集分成 K 折（此处 3 折），然后使用一个模型对其中一折进行预测，对其他折进行训练。

from sklearn.model_selection import cross_val_score
print(cross_val_score(sgd_clf, X_train, y_train_5, cv=3, scoring="accuracy"))

array([0.96595, 0.9486 , 0.95335])
虽然有96%的准确度，但是这个数据集只有10%的数据是5，所以如果有一个预测期全部预测为否也会有90%的准确度。
这也就是为什么精度常常不是很好地性能度量指标

2.混淆矩阵（更适合分类器）

关于混淆矩阵更详细的信息见西瓜书2.3.1 大体思路是：输出类别A被分类成类别 B 的次数。举个例子，为了知道分类器将 5 误分为 3 的次数，你需要查看混淆矩阵的第五行第三列。

ps:记住，只有当你处于项目的尾声，当你准备上线一个分类器的时候，你才应该使用测试集

第一步先获取预测值
第二步使用混淆矩阵，输入真实值和预测值

from sklearn.model_selection import cross_val_predict # 为每个输入数据点生成交叉验证的估计值
y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3)

from sklearn.metrics import confusion_matrix

confusion_matrix(y_train_5, y_train_pred)

array([[53428,  1151],
       [ 1491,  3930]])

混淆矩阵中的每一行表示一个实际的类, 而每一列表示一个预测的类。该矩阵的第一行认为“非5”（反例）中的 53272 张被正确归类为 “非 5”（他们被称为真反例，true negatives）, 而其余1307 被错误归类为”是 5” （假正例，false positives）。第二行认为“是 5” （正例）中的 1077被错误地归类为“非 5”（假反例，false negatives），其余 4344 正确分类为 “是 5”类（真正例，true positives）。一个完美的分类器将只有真反例和真正例，所以混淆矩阵的非零值仅在其主对角线（左上至右下）。

想要一个完美的准确率，一个平凡的方法是构造一个单一正例的预测和确保这个预测是正确的（ precision = 1/1 = 100% ）。但是这什么用，因为分类器会忽略所有样例，除了那一个正例。所以准确率一般会伴随另一个指标一起使用，这个指标叫做召回率（recall），也叫做敏感度

准确率和召回率（查准率和查全率）

是混淆矩阵的延伸，混淆矩阵中指标的比值

from sklearn.metrics import precision_score, recall_score

print(precision_score(y_train_5, y_train_pred)) print(recall_score(y_train_5, y_train_pred))

0.9187339606501284 0.594355285002767

当你去观察精度的时候，你的“数字 5 探测器”看起来还不够好。当它声明某张图片是 5 的时候，它只有 77% 的可能性是正确的。而且，它也只检测出“是 5”类图片当中的 79%。

通常结合准确率和召回率会更加方便，这个指标叫做“F1 值”，特别是当你需要一个简单的方法去比较两个分类器的优劣的时候。F1 值是准确率和召回率的调和平均。普通的平均值平等地看待所有的值，而调和平均会给小的值更大的权重。所以，要想分类器得到一个高的 F1 值，需要召回率和准确率同时高。

为了计算 F1 值，简单调用f1_score()

from sklearn.metrics import f1_score
f1_score(y_train_5, y_pred)

0.78468208092485547

准确率/召回率之间的折衷

为了弄懂这个折衷，我们看一下SGDClassifier是如何做分类决策的。对于每个样例，它根据决策函数计算分数,如果这个分数大于一个阈值，它会将样例分配给正例，否则它将分配给反例。图 3-3 显示了几个数字从左边的最低分数排到右边的最高分。假设决策阈值位于中间的箭头（介于两个 5 之间）：您将发现4个真正例（数字 5）和一个假正例（数字 6）在该阈值的右侧。因此,使用该阈值,准确率为 80%（4/5）。但实际有 6 个数字 5，分类器只检测 4 个, 所以召回是 67% （4/6）。现在，如果你提高阈值（移动到右侧的箭头），假正例（数字 6）成为一个真反例，从而提高准确率（在这种情况下高达 100%），但一个真正例变成假反例，召回率降低到 50%。相反，降低阈值可提高召回率、降低准确率。

Scikit-Learn 不让你直接设置阈值，但是它给你提供了设置决策分数的方法，这个决策分数可以用来产生预测。它不是调用分类器的predict()方法，而是调用decision_function()方法。这个方法返回每一个样例的分数值，然后基于这个分数值，使用你想要的任何阈值做出预测。

y_scores = sgd_clf.decision_function([some_digit])
y_scores
#array([ 161855.74572176])
threshold = 0
y_some_digit_pred = (y_scores > threshold)
#array([ True], dtype=bool)

应该如何使用哪个阈值呢？首先，你需要再次使用cross_val_predict()得到每一个样例的分数值，但是这一次指定返回一个决策分数，而不是预测值。

y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3, 
                            method="decision_function")

现在有了这些分数值。对于任何可能的阈值，使用precision_recall_curve(),你都可以计算准确率和召回率:

from sklearn.metrics import precision_recall_curve
precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores)

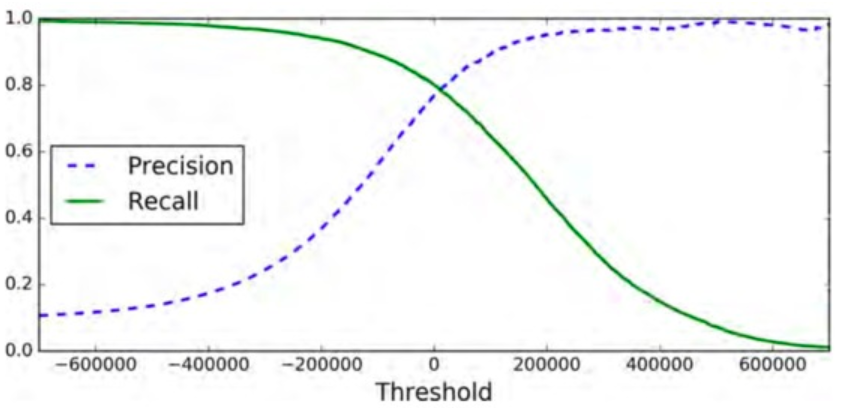
最后使用 Matplotlib 画出准确率和召回率，这里把准确率和召回率当作是阈值的一个函数。

def plot_precision_recall_vs_threshold(precisions, recalls, thresholds):
    plt.plot(thresholds, precisions[:-1], "b--", label="Precision")
    plt.plot(thresholds, recalls[:-1], "g-", label="Recall")
    plt.xlabel("Threshold")
    plt.legend(loc="upper left")
    plt.ylim([0, 1])
plot_precision_recall_vs_threshold(precisions, recalls, thresholds)
plt.show()

ROC 曲线

受试者工作特征（ROC）曲线是另一个二分类器常用的工具。它非常类似与准确率/召回率曲线，但不是画出准确率对召回率的曲线，ROC 曲线是真正例率（true positive rate，另一个名字叫做召回率）对假正例率（false positive rate, FPR）的曲线。FPR 是反例被错误分成正例的比率。它等于 1 减去真反例率（true negative rate， TNR）。TNR是反例被正确分类的比率。TNR也叫做特异性。所以 ROC 曲线画出召回率对（1 减特异性）的曲线。

为了画出 ROC 曲线，你首先需要计算各种不同阈值下的 TPR、FPR，使用roc_curve()函数：

from sklearn.metrics import roc_curve
fpr, tpr, thresholds = roc_curve(y_train_5, y_scores)

然后你可以使用 matplotlib，画出 FPR 对 TPR 的曲线。下面的代码生成图

def plot_roc_curve(fpr, tpr, label=None):
    plt.plot(fpr, tpr, linewidth=2, label=label)
    plt.plot([0, 1], [0, 1], 'k--')
    plt.axis([0, 1, 0, 1])
    plt.xlabel('False Positive Rate')
    plt.ylabel('True Positive Rate')
plot_roc_curve(fpr, tpr)
plt.show()

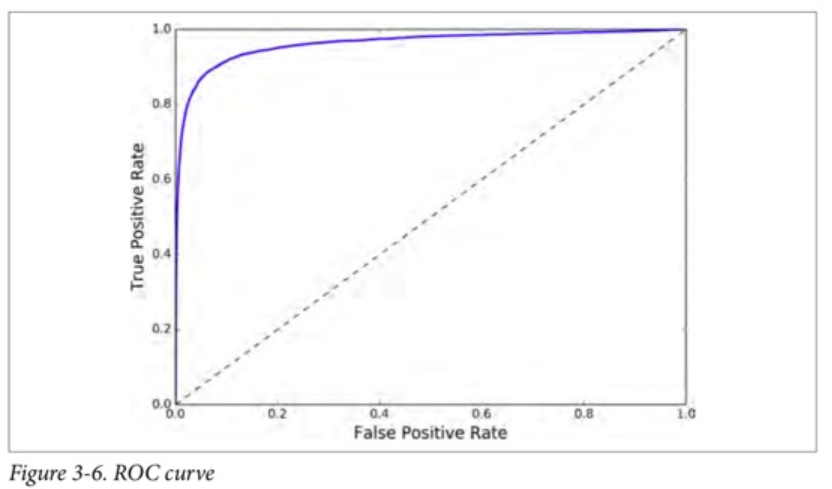
这里同样存在折衷的问题：召回率（TPR）越高，分类器就会产生越多的假正例（FPR）。图中的点线是一个完全随机的分类器生成的 ROC 曲线；一个好的分类器的 ROC 曲线应该尽可能远离这条线（即向左上角方向靠拢）。

一个比较分类器之间优劣的方法是：测量ROC曲线下的面积（AUC）。一个完美的分类器的 ROC AUC 等于 1，而一个纯随机分类器的 ROC AUC 等于 0.5。Scikit-Learn 提供了一个函数来计算 ROC AUC：

from sklearn.metrics import roc_auc_score
roc_auc_score(y_train_5, y_scores)
#0.97061072797174941

因为 ROC 曲线跟准确率/召回率曲线（或者叫 PR）很类似，你或许会好奇如何决定使用哪一个曲线呢？一个笨拙的规则是，优先使用 PR 曲线当正例很少，或者当你关注假正例多于假反例的时候。其他情况使用 ROC 曲线。举例子，回顾前面的 ROC 曲线和 ROC AUC 数值，你或许人为这个分类器很棒。但是这几乎全是因为只有少数正例（“是 5”），而大部分是反例（“非 5”）。相反，PR 曲线清楚显示出这个分类器还有很大的改善空间（PR 曲线应该尽可能地靠近右上角）。

多类分类

二分类器只能区分两个类，而多类分类器（也被叫做多项式分类器）可以区分多于两个类。

一些算法（比如随机森林分类器或者朴素贝叶斯分类器）可以直接处理多类分类问题。其他一些算法（比如 SVM 分类器或者线性分类器）则是严格的二分类器。然后，有许多策略可以让你用二分类器去执行多类分类。

举例子，创建一个可以将图片分成 10 类（从 0 到 9）的系统的一个方法是：训练10个二分类器，每一个对应一个数字（探测器 0，探测器 1，探测器 2，以此类推）。然后当你想对某张图片进行分类的时候，让每一个分类器对这个图片进行分类，选出决策分数最高的那个分类器。这叫做“一对所有”（OvA）策略（也被叫做“一对其他”）。

另一个策略是对每一对数字都训练一个二分类器：一个分类器用来处理数字 0 和数字 1，一个用来处理数字 0 和数字 2，一个用来处理数字 1 和 2，以此类推。这叫做“一对一”（OvO）策略。如果有 N 个类。你需要训练N*(N-1)/2个分类器。对于 MNIST 问题，需要训练 45 个二分类器！当你想对一张图片进行分类，你必须将这张图片跑在全部45个二分类器上。然后看哪个类胜出。OvO 策略的主要有点是：每个分类器只需要在训练集的部分数据上面进行训练。这部分数据是它所需要区分的那两个类对应的数据。

一些算法（比如 SVM 分类器）在训练集的大小上很难扩展，所以对于这些算法，OvO 是比较好的，因为它可以在小的数据集上面可以更多地训练，较之于巨大的数据集而言。但是，对于大部分的二分类器来说，OvA 是更好的选择。

Scikit-Learn 可以探测出你想使用一个二分类器去完成多分类的任务，它会自动地执行 OvA（除了 SVM 分类器，它使用 OvO）。让我们试一下SGDClassifier.

sgd_clf.fit(X_train, y_train) # y_train, not y_train_5
sgd_clf.predict([some_digit])
#array([ 5.])

很容易。上面的代码在训练集上训练了一个SGDClassifier。这个分类器处理原始的目标class，从 0 到 9（y_train），而不是仅仅探测是否为 5 （y_train_5）。然后它做出一个判断（在这个案例下只有一个正确的数字）。在幕后，Scikit-Learn 实际上训练了 10 个二分类器，每个分类器都产到一张图片的决策数值，选择数值最高的那个类。

为了证明这是真实的，你可以调用decision_function()方法。不是返回每个样例的一个数值，而是返回 10 个数值，一个数值对应于一个类。

some_digit_scores = sgd_clf.decision_function([some_digit])
some_digit_scores
#array([[-311402.62954431, -363517.28355739, -446449.5306454 ,
        -183226.61023518, -414337.15339485, 161855.74572176,
        -452576.39616343, -471957.14962573, -518542.33997148,
        -536774.63961222]])

最高数值是对应于类别 5 ：

np.argmax(some_digit_scores)
#5
sgd_clf.classes_
#array([ 0., 1., 2., 3., 4., 5., 6., 7., 8., 9.])
sgd_clf.classes_[5]
#5.0

一个分类器被训练好了之后，它会保存目标类别列表到它的属性classes_ 中去，按照值排序。在本例子当中，在classes_ 数组当中的每个类的索引方便地匹配了类本身，比如，索引为 5 的类恰好是类别 5 本身。但通常不会这么幸运。

误差分析

探索准备数据的候选方案，尝试多种模型，把最好的几个模型列为入围名单，用GridSearchCV调试超参数，尽可能地自动化，像你前面的章节做的那样。在这里，我们假设你已经找到一个不错的模型，你试图找到方法去改善它。一个方式是分析模型产生的误差的类型。

首先，你可以检查混淆矩阵。你需要使用cross_val_predict()做出预测，然后调用confusion_matrix()函数，像你早前做的那样。

y_train_pred = cross_val_predict(sgd_clf, X_train_scaled, y_train, cv=3)
conf_mx = confusion_matrix(y_train, y_train_pred)
conf_mx
#array([[5725, 3, 24, 9, 10, 49, 50, 10, 39, 4],
        [ 2, 6493, 43, 25, 7, 40, 5, 10, 109, 8],
        [ 51, 41, 5321, 104, 89, 26, 87, 60, 166, 13],
        [ 47, 46, 141, 5342, 1, 231, 40, 50, 141, 92],
        [ 19, 29, 41, 10, 5366, 9, 56, 37, 86, 189],
        [ 73, 45, 36, 193, 64, 4582, 111, 30, 193, 94],
        [ 29, 34, 44, 2, 42, 85, 5627, 10, 45, 0],
        [ 25, 24, 74, 32, 54, 12, 6, 5787, 15, 236],
        [ 52, 161, 73, 156, 10, 163, 61, 25, 5027, 123],
        [ 43, 35, 26, 92, 178, 28, 2, 223, 82, 5240]])

这里是一对数字。使用 Matplotlib 的matshow()函数，将混淆矩阵以图像的方式呈现，将会更加方便。

plt.matshow(conf_mx, cmap=plt.cm.gray)
plt.show()

这个混淆矩阵看起来相当好，因为大多数的图片在主对角线上。在主对角线上意味着被分类正确。数字 5 对应的格子看起来比其他数字要暗淡许多。这可能是数据集当中数字 5 的图片比较少，又或者是分类器对于数字 5 的表现不如其他数字那么好。

多标签分类

到目前为止，所有的样例都总是被分配到仅一个类。有些情况下，你也许想让你的分类器给一个样例输出多个类别。比如说，思考一个人脸识别器。如果对于同一张图片，它识别出几个人，它应该做什么？当然它应该给每一个它识别出的人贴上一个标签。比方说，这个分类器被训练成识别三个人脸，Alice，Bob，Charlie；然后当它被输入一张含有 Alice 和 Bob 的图片，它应该输出[1, 0, 1]（意思是：Alice 是，Bob 不是，Charlie 是）。这种输出多个二值标签的分类系统被叫做多标签分类系统。

from sklearn.neighbors import KNeighborsClassifier
y_train_large = (y_train >= 7)
y_train_odd = (y_train % 2 == 1)
y_multilabel = np.c_[y_train_large, y_train_odd]
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train, y_multilabel)

这段代码创造了一个y_multilabel数组，里面包含两个目标标签。第一个标签指出这个数字是否为大数字（7，8 或者 9），第二个标签指出这个数字是否是奇数。接下来几行代码会创建一个KNeighborsClassifier样例（它支持多标签分类，但不是所有分类器都可以），然后我们使用多目标数组来训练它。现在你可以生成一个预测，然后它输出两个标签：

knn_clf.predict([some_digit])
array([[False, True]], dtype=bool)

它工作正确。数字 5 不是大数（False），同时是一个奇数（True）。

有许多方法去评估一个多标签分类器，和选择正确的量度标准，这取决于你的项目。举个例子，一个方法是对每个个体标签去量度 F1 值（或者前面讨论过的其他任意的二分类器的量度标准），然后计算平均值。下面的代码计算全部标签的平均 F1 值：

y_train_knn_pred = cross_val_predict(knn_clf, X_train, y_train, cv=3)
f1_score(y_train, y_train_knn_pred, average="macro")
#0.96845540180280221

这里假设所有标签有着同等的重要性，但可能不是这样。特别是，如果你的 Alice 的照片比 Bob 或者 Charlie 更多的时候，也许你想让分类器在 Alice 的照片上具有更大的权重。一个简单的选项是：给每一个标签的权重等于它的支持度（比如，那个标签的样例的数目）。为了做到这点，简单地在上面代码中设置average="weighted"。

多输出分类

我们即将讨论的最后一种分类任务被叫做“多输出-多类分类”（或者简称为多输出分类）。它是多标签分类的简单泛化，在这里每一个标签可以是多类别的（比如说，它可以有多于两个可能值）。

为了说明这点，我们建立一个系统，它可以去除图片当中的噪音。它将一张混有噪音的图片作为输入，期待它输出一张干净的数字图片，用一个像素强度的数组表示，就像 MNIST 图片那样。注意到这个分类器的输出是多标签的（一个像素一个标签）和每个标签可以有多个值（像素强度取值范围从 0 到 255）。所以它是一个多输出分类系统的例子。

分类与回归之间的界限是模糊的，比如这个例子。按理说，预测一个像素的强度更类似于一个回归任务，而不是一个分类任务。而且，多输出系统不限于分类任务。你甚至可以让你一个系统给每一个样例都输出多个标签，包括类标签和值标签。

让我们从 MNIST 的图片创建训练集和测试集开始，然后给图片的像素强度添加噪声，这里是用 NumPy 的randint()函数。目标图像是原始图像。

noise = rnd.randint(0, 100, (len(X_train), 784))
noise = rnd.randint(0, 100, (len(X_test), 784))
X_train_mod = X_train + noise
X_test_mod = X_test + noise
y_train_mod = X_train
y_test_mod = X_test

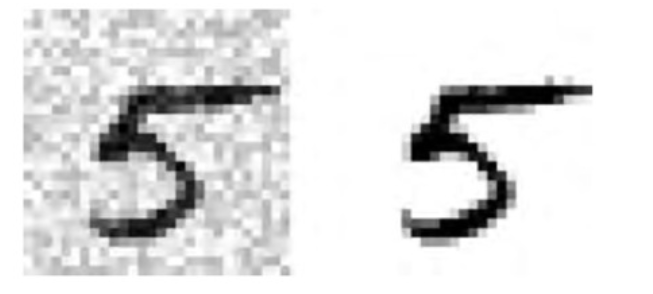
左边的加噪声的输入图片。右边是干净的目标图片。现在我们训练分类器，让它清洁这张图片：

knn_clf.fit(X_train_mod, y_train_mod)
clean_digit = knn_clf.predict([X_test_mod[some_index]])
plot_digit(clean_digit)

看起来足够接近目标图片。现在总结我们的分类之旅。希望你现在应该知道如何选择好的量度标准，挑选出合适的准确率/召回率的折衷方案，比较分类器，更概括地说，就是为不同的任务建立起好的分类系统。

posted @ 2019-08-08 17:35 秋雨秋雨秋雨阅读(1240) 评论(0) 编辑收藏举报

刷新页面返回顶部

秋雨秋雨秋雨