二项分布。计算binomial(100,50,0.25)将会产生的递归调用次数(算法第四版1.1.27)
算法第四版35页问题1.1.27,估计用一下代码计算binomial(100,50,0.25)将会产生的递归调用次数:
public static double binomial(int n,int k,double p){ if(n == 0 && k == 0) return 1.0; if(n<0 || k<0) return 0.0; return (1.0-p)*binomial(n-1,k,p) +p*binomial(n-1,k-1,p) }
虽然书上只让估计调用次数,但是觉得想知道到底调用了几次。
我用图画出递归调用的情况
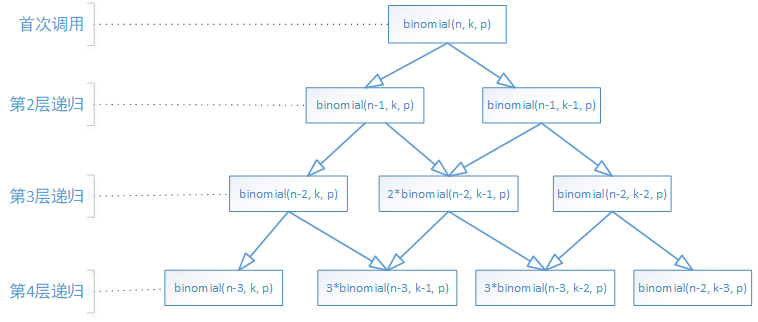
可以看出递归中有很多重复调用比如,第4层递归 分别调用了binomial(n-3,k-1,p)和binomial(n-3,k-2,p)三次。这就是这个算法效率低的原因。可以看出重复调用的次数是一个杨辉三角。
根据杨辉三角的性质,
第m层递归函数被调用的情况为:
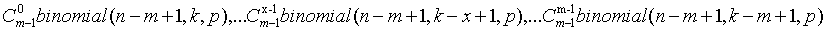
第m层第x(x<=m)项为:

但是有些调用实际上不会发生,结合函数的返回条件:
if(n == 0 && k == 0) return 1.0; if(n<0 || k<0) return 0.0;
设我们传入的初始参数为n=N,k=K 则,可以得出已下结论:
- 当m=N+1且x=K+1时,满足程序退出的第一个条件;
- 当m>N+1或x>K+1时,满足程序退出的第二个条件(根据杨辉三角的性质,第m行有m项,所有此时有K+1<x<=m)
让我们看看满足以上结论的详细项:
1.下列递归调用的x>K+1,满足结论2:
-
- m=K+2行的第K+2项:
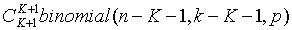
- m=K+3行的第K+2项到K+3项:
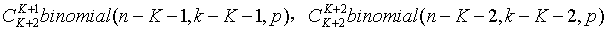
- ……
- m=N+1行的第K+2项到最后一项:
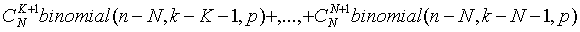
- m=K+2行的第K+2项:
2.m=N+1行的第K+1项递归调用的第一个参数n和第二个参数k均为0,满足结论1。
3.当m=N+2时,显然m>N+1,满足结论2;
如果调用 参数满足函数退出条件,那么由
参数满足函数退出条件,那么由 调用的递归实际上就不会发生,数量为
调用的递归实际上就不会发生,数量为 的系数✖️2。
的系数✖️2。
N+2之后的递归都不会发生,所以做计算时只考虑到N+2层。N+2层的无效调用数量,为N+1层满足结论1或2的调用的数量*2,一次类推,直到K+3层的无效调用数量,为K+2层满足结论1或2的调用数量*2;K+2层到1层上,所有调用都有效;因为K+1层到1层,没有调用满足结论1或2.
根据杨辉三角的性质:从第1层到第N+2层所有的系数和为 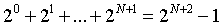
其中不会实际发生的调用次数为从(K+2层到N+1层):
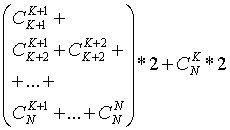
化简之后为:
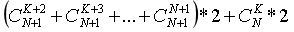
再次化简
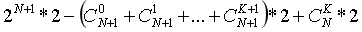
所以最后程序递归调用的总次数为
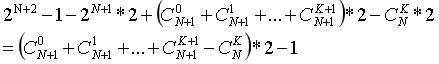
运行随机验证几个组合,可以证明上述公式是正确的!




