如何理解补码
在计算机系统中,数值一律用补码来表示和存储。原因在于,使用补码,可以将符号位和数值域统一处理;
在理解补码的之前,得先了解另外一个概念:补数;以十进制为例,不考虑负数,1位十进制数能表示的最大的数是9,最小是0。由于进位的原因,0-1=0+9会得到9。9是-1以10为模的补数,目前来看,这东西根本没啥用!!没错,对人来说确实没啥用,但对计算机来说不一样,在计算机中所有的信息都是以二进制来表示的,所有的信息都用0和1表示,专门留出1个位表示正负号,不但浪费资源,做计算时也不方便。所以,天才的计算机科学家(具体是谁不知道,一说是冯诺依曼)利用补码,不但能正确的表示负数,而且还将加减乘除均运算都转换成简单的加法运算,现在我们来看看他/她是怎么做到的吧:
以4位二进制做例子,先把能表示的数字放到一个表盘上,外圈为二进制,内圈为10进制:
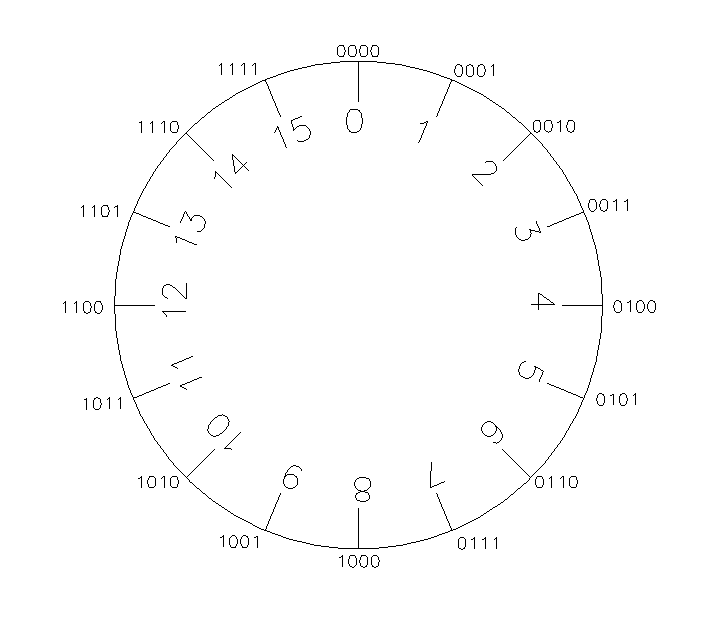
根据上述补数的原理可知,在上面这个表盘中如果有一个数x,那么:
x - 1 = x + (-1) +16 = x +15
x - 2 = x + (-2) +16 = x +14
......
x - 7 = x + (-7) +16 = x + 9
x - 8 = x + (-8) +16 = x + 8
x - 9 = x + (-9) +16 = x + 7
x - 10 = x + (-10) +16 = x +6
......
x - 15 = x + (-15) +16 = x + 1
x - 8 = x + (-8) +16 = x + 8
x - 9 = x + (-9) +16 = x + 7
x - 10 = x + (-10) +16 = x +6
......
x - 15 = x + (-15) +16 = x + 1
是不是有灵感了,不是不能表示负数吗?那咱们用15表示-1,用14表示-2,……,用8表示-8,所有的加法(减法、乘法、除法运算均可以转换为加法)运算结果在上述表盘上的结果都不会收到影响!!这样在上述表盘就可以表示-8~+7之间所有的整数。用来表示-1的二进制码就是-1的补码(1111)。
我们把结果画到图上,结果如下:
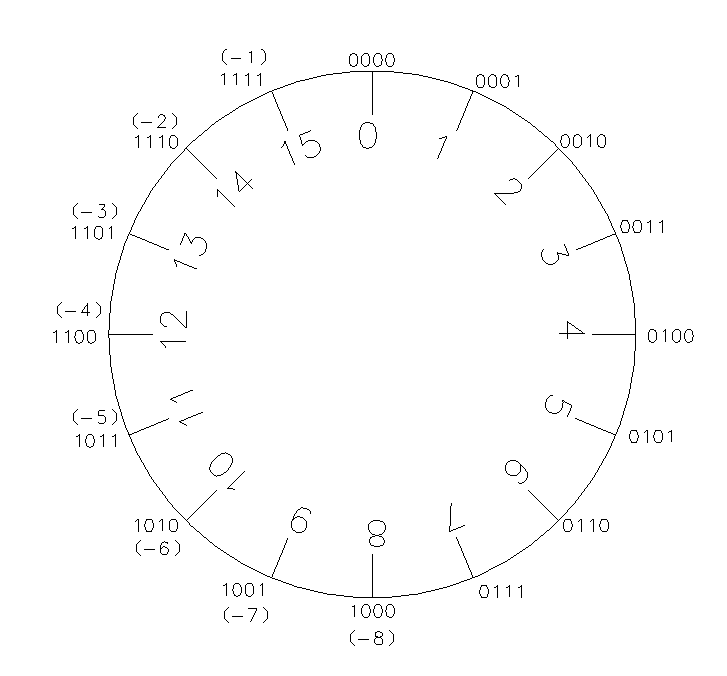
注意所有的运算只有在上述表盘中才成立,上述的结论脱离了对应的表盘就是不成立。同时我们只是用15表示了-1,因为这样替换不影响计算结果,并不是说15就等于-1,这里面有区别。
是不是觉得万事大吉了?然而并没有!!!
在上述表盘中试试计算下6+7 或者-7+(-8),是不是觉得有点失望,完全不是想要的结果!这就是溢出,因为上述表盘只能表示-8~+7之间的数,如果计算结果超出这个范围就会出现错误,如何检测整型相加溢出。
还有一个重要问题:在学习补码的时候,很多教材、文章说求补码的过程先求反码、再求补码,给人的感觉是补码由于反码推导出来的,其实不是,这是误导!!!如果按照先求反码,再求补码的过程来理解补码,就会感到迷茫。我在这个坑里待了好久才跳出来。还好有一篇文章提醒了我,但是现在找不着出处了,原作者如果看到,请提醒我加链接。




