简析方差、标准差与数值离散程度

方差（variance）: 变量与其均值的差的平方和除以(变量数+1)。

　　 如有一组数据: [1,2,3,4,5], 其均值就是 (1+2+3+4+5) / 5 = 3

　　 所以其方差为: （(1-3)^2 + (2-3)^2 +(3-3)^2 + (4-3)^2 + (5-3)^2） /（ 5+1） = 1.6666....

　　

 

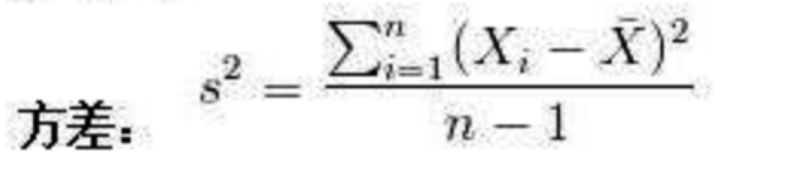
标准差(standard deviation)：方差的算术平方根

　　

 

方差和标准差反应了一组数据的离散程度:

当方差越小时，数据的离散程度越小

而当方差越大时，数据的离散程度也就越大。

如有两组数据

A = [1,2,3,4,5]

B=[1,5,7,9,11]

A 的方差为2 、B的方差为11.84 ，从方差的大小比较，var(A)<var(B)

所以B的离散程度比A的离散程度高

 

为什么方差可以体现数据的离散程度？

由公式可知:

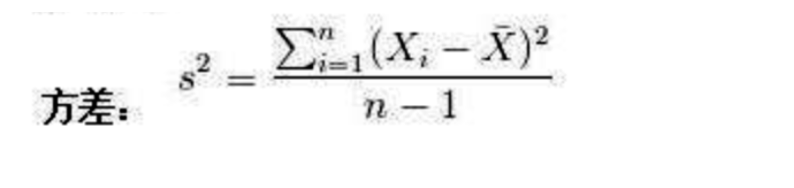
当所有的变量值都一样时，均值等于变量值

所以方差为0,此时离散程度为0。当各个变量值里均值都有一定距离时

方差大于0。

 

例子:

通过使用 from sklearn.datasets.samples_generator import make_blobs 围绕3个中心点来生成数据集

红色的点代表 中心点

蓝色的点代表 生成点

通过修改make_blobs里面的cluster_std参数来控制 生成点 与 中心点之间的离散程度。而cluster_std参数

对应就是标准差

（1）当标准差为 0.60时:

(2) 当标准差为 0.3时

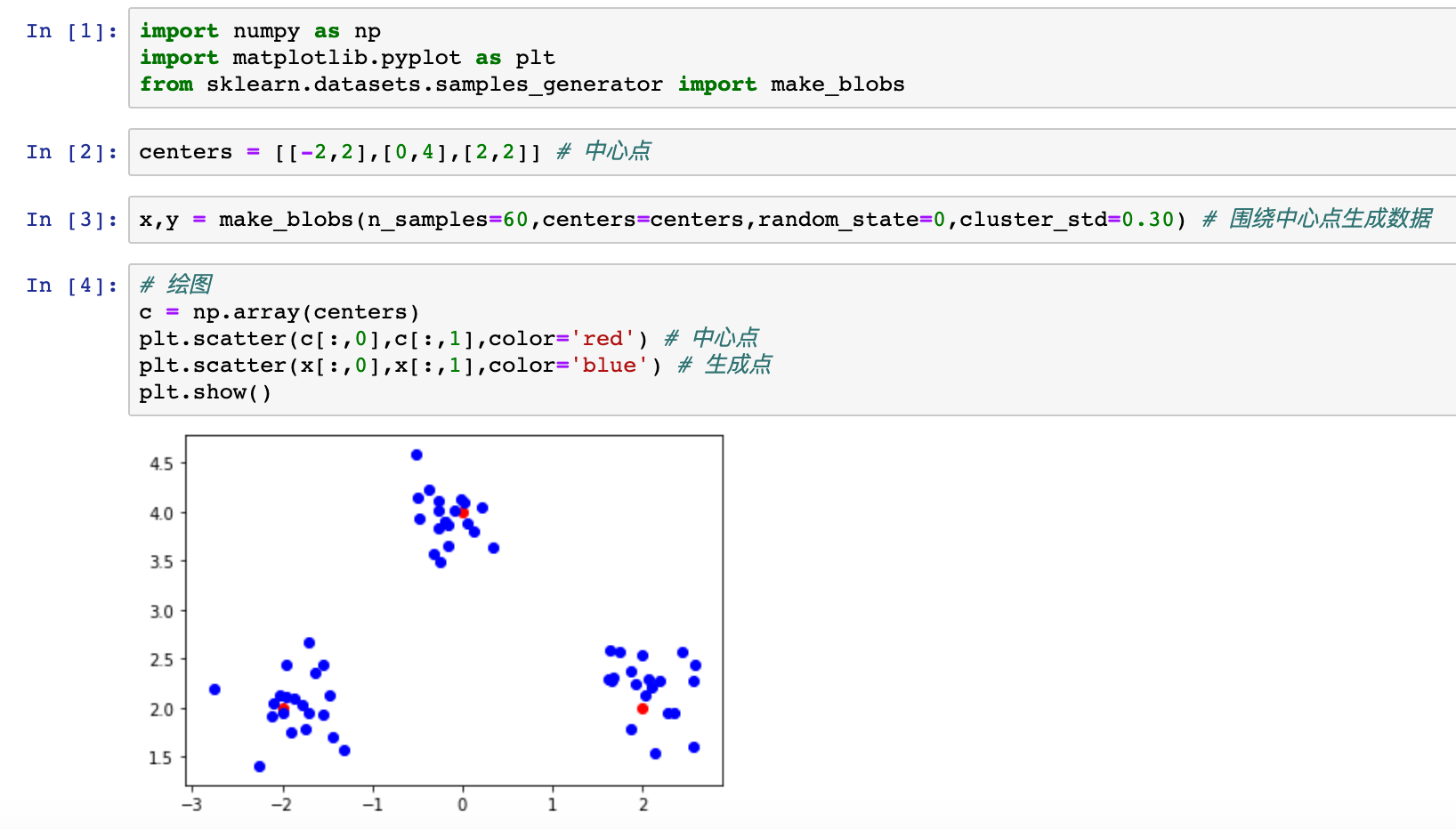
图像反映了不同标准差之间数据发布的情况

   

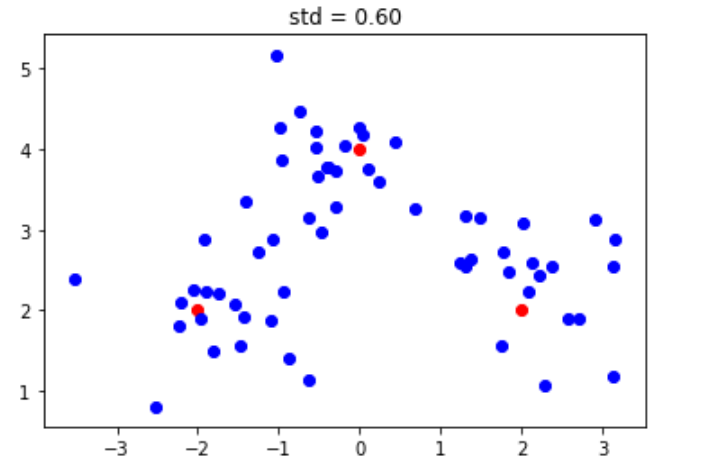
由此也反映了标准差与数值离散程度之间的对应关系。