动态规划算法

---恢复内容开始---

钢条切割

有钢条收益

钢条长度　　1, 2, 3, 4, 5, 6, 7, 8, 9, 10
钢条收益　　1, 5, 8, 9, 10, 17, 17, 20, 24, 30

求长度为n的钢条最优切割方案？

自顶向下递归实现

static void Main(string[] args)
{
    //分别表示长度为0,1..10的收益
    var prices = new int[] { 0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30 };
    int receipt = CutRod(prices, 4);
    Console.WriteLine(receipt);
}
//表示长度为n的最大收益
static int CutRod(int[] p, int n)
{
    if (n == 0)
        return 0;
    int q1 = int.MinValue;
    //表示先切割长度i
    for (int i = 1; i <= n; i++)
    {
        //剩余部分的收益
        int q2 = CutRod(p, n - i);
        q1 = q1 > p[i] + q2 ? q1 : p[i] + q2;
    }
    Console.Write(n + " ");
    Console.WriteLine(q1);
    return q1;
}

自顶向下会遍历每一条求解路径：

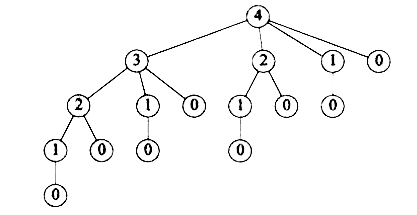
其中每一个路径表示一个求解过程。比如求f4=f1+f3，f3又有3个求解方法等等。
这种求解方法需要求解路径上的所有项，即使有些已经求过的，也会重复求解。

动态规划方法求解这个问题，有两种等价的方法

带备忘的自顶向下法：存储已经求解的子问题，下次用到时直接使用
自地上向：求解最小的子问题，然后次小的子问题通过已经求解的子问题求解，直到得到原问题。

备忘的自顶向下法

static void Main(string[] args)
{
    //分别表示长度为1..10的收益
    var prices = new int[] { 0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30 };
    int receipt = MemoizedCutRod(prices, 10);
    Console.WriteLine(receipt);
}
static int MemoizedCutRod(int[] p, int n)
{
    //构造备忘存储位置
    int[] r = new int[n + 1];
    for (int i = 0; i <= n; i++)
        r[i] = int.MinValue;
    return MemoizedCutRodAux(p, n, r);
}
//r中表示下标为长度的最大收益
private static int MemoizedCutRodAux(int[] p, int n, int[] r)
{
    //使用已经备忘（memoirization）的结果
    if (r[n] >= 0)
        return r[n];
    int q1 = int.MinValue;
    if (n == 0)
        q1 = 0;
    else
    {
        for (int i = 1; i <= n; i++)
        {
            int q2 = MemoizedCutRodAux(p, n - i, r);
            q1 = q1 > p[i] + q2 ? q1 : p[i] + q2;
        }
    }
    r[n] = q1;
    return q1;
}

自底向下

static void Main(string[] args)
{
    //分别表示长度为1..10的收益
    var prices = new int[] { 0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30 };
    int receipt = BottomUpCutRod(prices, 10);
    Console.WriteLine(receipt);
}
static int BottomUpCutRod(int[] p, int n)
{
    //构造子问题存储位置
    int[] r = new int[n + 1];
    r[0] = 0;//最小子问题
    for (int j = 1; j <= n; j++)
    {
        int q = int.MinValue;
        //求解长度为j的子问题，分解为比j小的子问题
        for (int i = 1; i <= j; i++)
            q = q > p[i] + r[j - i]? q : p[i] + r[j - i];
        r[j] = q;
    }
    return r[n];
}

动态规划原理：

适合应用动态规划方法求解的最优化问题具备两个要素，最优子结构和子问题重叠。

如果一个问题最优解包含子问题的最优解，则这个问题具有最优子结构性质。
子问题空间必须足够小，也就是递归算法会反复求解子问题，而不是生成新的子问题。

最后将子问题进行重构得到重构后的最优解。

最长子序（longest common subsequence LCS）问题

如果有x=ABCBDAB，z=BCDB，其中z对应于x递增的下标2 3 5 7，则z是x的一个子序。对于x和y两个序列，可以使用动态规划求解其最长的公共子序。

X=x1...xm，Y=y1..yn，任意子序列Z=z1..zk

如果xm=yn，则zk=xm=yn，且zk-1是xm-1和yn-1的一个LCS
如果xm != yn，则zk != xm意味着Z是Xm-1和Y的一个LCS
如果xm != yn，则zk != yn意味着Z是X和Yn-1的一个LCS

由此得到递推公式，其中c[i,j]表示Xi和Yj的LCS长度
| 0 if i==0 || j==0
c[i,j]=| c[i-1,j-1]+1 if i>0 && j>0 && xi==yi
| max(c[i,j-1],c[i-1]) if i>0 && j>0 && xi!=yi

不用迭代求解方法，也可以使用一个自底向上的计算。
可以通过子问题保存，最后求得原问题。其中使用存储表c[0..m, 0..n]中的c[i,j]表示表示Xi和Yj的LCS长度

static void Main(string[] args)
{
    //第一个字符无意义
    var X = new char[] { '\0', 'A', 'B', 'C', 'B', 'D', 'A', 'B' };
    var Y = new char[] { '\0', 'B', 'D', 'C', 'B', 'A' };
    int[,] c;
    string[,] b;
    LcsLength(X, Y, out c, out b);
    for (int i = 1; i < X.Length; i++)
    {
        for (int j = 1; j < Y.Length; j++)
        {
            Console.Write(c[i, j] + "  ");
        }
        Console.WriteLine();
    }
    for (int i = 1; i < X.Length; i++)
    {
        for (int j = 1; j < Y.Length; j++)
        {
            Console.Write(b[i, j] + " ");
        }
        Console.WriteLine();
    }
    Console.WriteLine();
}
//X，Y的第一个字符没有用
static void LcsLength(char[] X, char[] Y,out int[,] c,out string[,] b)
{
    //构造子问题存储位置
    c = new int[X.Length, Y.Length];
    b = new string[X.Length, Y.Length];

    //最小子问题结果
    for (int i = 0; i < X.Length; i++)
    {
        c[i, 0] = 0;
    }

    for (int i = 1; i < X.Length; i++)
    {
        for (int j = 1; j < Y.Length; j++)
        {
            if (X[i] == Y[j])
            {
                c[i, j] = c[i - 1, j - 1] + 1;
                b[i, j] = "↖";
            }
            else if (c[i - 1, j] >= c[i, j - 1])
            {
                c[i, j] = c[i - 1, j];
                b[i, j] = "↑";
            }
            else
            {
                c[i, j] = c[i, j - 1];
                b[i, j] = "←";
            }
        }
    }
}

看出算法会占用两块i*j大小的内存，通过优化，可以省去b。一个节点的下一走向只有三个方向，我可以判断出来。

*最优二叉搜索树

posted on 2016-02-28 22:58 峰入云阅读(310) 评论(0) 编辑收藏举报

刷新页面返回顶部

峰入云

动态规划算法

导航