红黑树

二叉搜索树基本操作都可以在O(h)内完成，然而数的高度较高时，可能并不比在链表上执行的快。红黑树是平衡搜索树中的一种保证在最坏情况下时间复杂度为O(lg(n))

红黑树的性质

1. 每个节点或是红色或是黑色
2. 根节点是黑色的
3. 每个叶节点是黑色的
4. 如果一个节点是红色，则两个子节点是黑色的
5. 每个节点，到后代叶子节点的路径上，包含相同数目的黑色节点

因为叶子节点是null，没有办法存储颜色，所以用一个哨兵nil，其他属性p、left、right、key是任意值(null)为好。

由红黑树的性质可知，h最大为2lg(n+1)

旋转操作

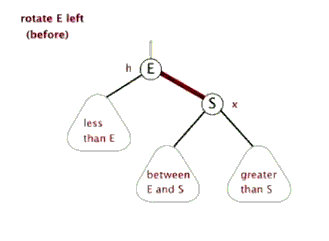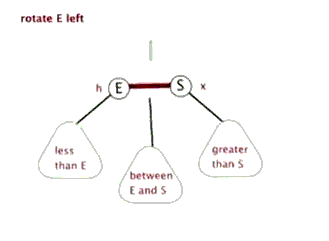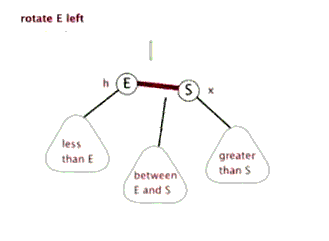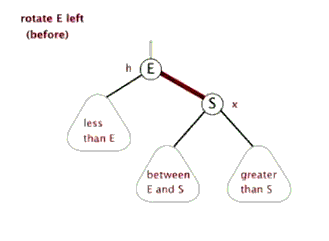
图片来源，其中关于红黑树的介绍更详细

LeftRotate(T, h)
{
    x = h.right;
    //x的左子树成为h的右子树
    h.right = x.left;
    if (x.left != T.nil)
        x.left.parent = h;
    //x的parent是h的parent
    x.parent = h.parent;
    //h的parent对应h的子树，成为x
    if (h.parent == T.nil)
        T.root = x;
    else if (h == h.parent.left)
        h.parent.left = x;
    else
        h.parent.right = x;
    //将x的左子树设置为h
    x.left = h;
    h.parent = y;
}

RightRotate(T, x)
{
    h = x.left;
    //h的右子树成为x的左子树
    x.left = h.right;
    if (h.right != T.nil)
        h.right.parent = x;
    //h的parent是x的parent
    h.parent = x.parent;
    //x的parent对应x的子树，成为h
    if (x.parent == T.nil)
        T.root = h;
    else if (x == x.parent.right)
        x.parent.right = h;
    else
        x.parent.left = h;
    //将h的右子树设置为x
    h.right = x;
    x.parent = y;
}

插入操作

插入操作与搜索二叉树操作基本相同。需要注意的是

1. null被nil代替
2. 插入的元素的子树置为nil
3. 对插入的元素设置红色
4. 对插入的元素进行RbInsertFixup，保证符合红黑树性质

TreeInsert(T, z)
{
    y = T.nil;
    x = T.root;
    while (x != T.nil)
    {
        y = x;
        if (z.key < x.key)
            x = x.left;
        else
            x = x.right;
    }
    x.parent = y;
    if (y == T.nil)
        T.root = z;
    else if (z.key < y.key)
        y.left = z;
    else
        y.right = z;
    z.left = z.right = T.nil;
    z.color = RED;
    RbInsertFixup(T, z);
}

理解RbInsertFixup

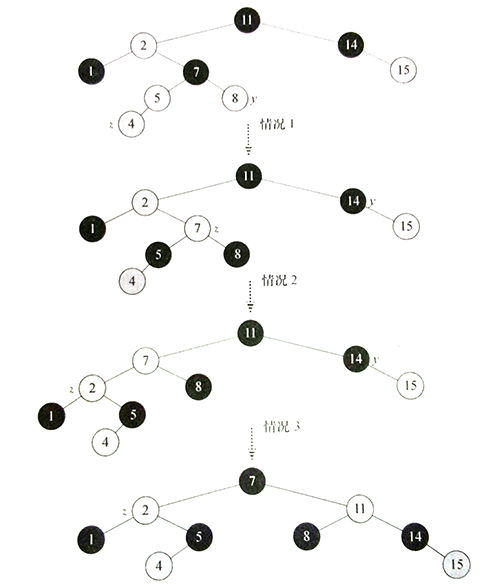
1. 插入z，由于z和父节点z.p都是red，违反了红黑树的性质。由于z的叔节点y是red，对应于情况1。节点重新上色，z上升一位，成为了第二幅图
2. z和父节点再次违规，z的叔节点是黑色的。因为z是z父节点的右孩子，对应于情况2。执行一次左旋，得到第三幅图
3. z是父节点的左孩子，重新上色，执行右旋得到第四幅图
4. 成为合法的红黑树

RbInserFixup(T, z)
{
    while (z.parent.color == RED)
    {
        if (z.parent == z.parent.parent.left)
        {
            y = z.parent.parent.right;
            if (y.color == RED)
            {
                z.parent.color = BLACK;
                y.color = BLACK;
                z.parent.parent.color = RED;
                z = z.parent.parent;
            }
            else if (z == z.parent.right)
            {
                z = z.parent;
                LeftRotate(T, z);
            }
            z.parent.color = BLACK;
            z.parent.parent.color = RED;
        }
        else//将伤医情况的right与left换一下
        {
            y = z.parent.parent.left;
            if (y.color == RED)
            {
                z.parent.color = BLACK;
                y.color = BLACK;
                z.parent.parent.color = RED;
                z = z.parent.parent;
            }
            else if (z == z.parent.left)
            {
                z = z.parent;
                LeftRotate(T, z);
            }
            z.parent.color = BLACK;
            z.parent.parent.color = RED;
        }
    }
}

删除操作

情况与二叉搜索树类比。首先需要一个Transplant应用到红黑树上

RbTransplant(T, u, v)
{
    if (u.parent == T.nil)
        T.root = v;
    else if (u == u.parent.left)
        u.parent.left = v;
    else
        u.parent.right = v;
    v.parent = u.parent;
}

然后执行删除

RbTreeDelete(T, z)
{
    y = z;
    yOriginalColor = y.color;
    if (z.left == T.nil)
    {
        x = z.right;
        RbTransplant(T, z, z.right);
    }
    else if (z.right == T.nil)
    {
        x = z.left;
        RbTransplant(T, z, z.left);
    }
    else
    {
        y = TreeMinimum(z.right);//z有双子，则后继为右侧最小
        yOriginalColor = y.color;
        x = y.right;
        if (y.parent == z)
        {
            x.parent = y;
        }
        else
        {
            BrTransplant(T, y, y.right);
            y.right = z.right;
            y.right.parent = y;
        }
        BrTransplant(T, z, y);
        y.left = z.left;
        y.left.p = y;
        y.color = z.color;
    }
    if (yOriginalColor == BLACK)
        RbDeleteFixup(T, x);
}

RbDeleteFixup(T, x)
{
    while (x != T.root && x.color == BLACK)
    {
        if (x == x.parent.left)
        {
            w = x.parent.right;
            if (w.color == RED)
            {
                w.color = BLACK;
                x.p.color = RED;
                LeftRotate(T, x.parent);
                w = x.parent.right;
            }
            if (w.left.color == BLACK && w.right.color == BLACK)
            {
                w.color = RED;
                x = x.parent;
            }
            else
            {
                w.left.color = BLACK;
                w.color = RED;
                RightRotate(T, w);
                w.x.parent.right;
            }
            w.color = x.parent.color;
            x.parent.color = BLACK;
            w.right.color = BLACK;
            LeftRotate(T, x.p);
            x = T.root;
        }
        else //change right and left
        {
            w = x.parent.left;
            if (w.color == RED)
            {
                w.color = BLACK;
                x.p.color = RED;
                LeftRotate(T, x.parent);
                w = x.parent.left;
            }
            if (w.right.color == BLACK && w.left.color == BLACK)
            {
                w.color = RED;
                x = x.parent;
            }
            else
            {
                w.right.color = BLACK;
                w.color = RED;
                RightRotate(T, w);
                w.x.parent.left;
            }
            w.color = x.parent.color;
            x.parent.color = BLACK;
            w.left.color = BLACK;
            LeftRotate(T, x.p);
            x = T.root;
        }
    }
    x.color = BLACK;
}

 对红黑树的Extent

 

::动态顺序统计

在红黑树的每个节点中加入一个size属性，表示这棵树的节点数，其中哨兵的节点数size为0。则

x.size=x.left.size+z.right.size+1