搜索与图论篇——DFS和BFS
搜索与图论篇——DFS和BFS
本次我们介绍搜索与图论篇中DFS和BFS,我们会从下面几个角度来介绍:
- DFS和BFS简介
- DFS数字排序
- DFS皇后排序
- DFS树的重心
- BFS走迷宫
- BFS八数码
- BFS图层次
DFS和BFS简介
首先我们先来介绍一下DFS和BFS:
- DFS:深度优先遍历算法,我们在进行算法运算时,优先将该路径的当前路径执行完毕,执行完毕或失败后向上回溯尝试其他途径
- BFS:广度优先遍历算法,我们在进行算法运算时,优先将当前路径点的所有情况罗列出来,然后根据罗列出来的情况罗列下一层
DFS和BFS的算法依据:
- 两者均以树的形式进行展开,可以采用树的模型来进行DFS和BFS演示
DFS数字排序
我们首先给出DFS的一元问题:
- 给定一个整数n,将数字1∼n排成一排,将会有很多种排列方法。
- 现在,请你按照字典序将所有的排列方法输出。
问题解析:
/*一元问题解析*/
我们目前采用DFS算法运算,我们需要一次得到数据,然后回溯
那么我们目前的问题就是:
- 如何判断DFS算法结束:我们只需要记录遍历到第几个数字然后与之判断是否相等,若相等表示结束
- 如何得知当前数字已经使用:我们只需要单列一个数组来记录该数是否被使用即可
我们给出算法代码:
import java.util.Scanner;
public class Main {
public static final int N = 10;
// 存放数据
static int n;
static int[] arr = new int[N];
static int[] res = new int[N];
// 判断是否被使用
static boolean[] isUsed = new boolean[N];
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
n = scanner.nextInt();
for (int i = 0; i < n; i++) {
arr[i] = i+1;
}
dfs(0);
}
public static void dfs(int x){
// 首先判断是否可以输出
if (x == n){
for (int i=0;i < n;i++){
System.out.print(res[i]+ " ");
}
System.out.println();
}
// 开始dfs
for (int i = 0; i < n; i++) {
// 判断是否被使用,若被使用,则不能使用;若未被使用,使用并进入下一层
if (!isUsed[i]){
// 未被使用,使用并进入下一层
res[x] = arr[i];
isUsed[i] = true;
dfs(x+1);
// 下面属于回溯部分,我们需要恢复原样,这里的x已经回溯,不需要覆盖res的值
isUsed[i] = false;
}
}
}
}
DFS皇后排序
我们首先给出DFS的二元问题:
- n−皇后问题是指将n个皇后放在n×n的国际象棋棋盘上,使得皇后不能相互攻击到
- 即任意两个皇后都不能处于同一行、同一列或同一斜线上。
- 现在给定整数 nn,请你输出所有的满足条件的棋子摆法。
问题解析:
/*原始方法*/
首先我们采用最基本的思想,我们采用一元思想,针对n*n的棋盘上的每个位置都进行DFS操作,并对其判断是否满足条件
在满足条件的位置上我们放上皇后并记录数目,如果到最后皇后的数量足够,那么我们就将他输出
/*升级方法*/
我们已经知道他们不能放在同一行和同一列,我们直接采用for将一行中的一个位置选出来,然后对每行DFS操作并判断是否满足条件
在满足条件的位置上我们放上皇后并记录数目,如果到最后皇后的数量足够,那么我们就将他输出
/*注意点*/
我们的n-皇后问题还需要保证对角线上不具有相同棋子
我们采用二元函数的函数y=x以及y=n-x来给出对角线的位置
我们给出算法代码:
/*原始方法*/
import java.util.Scanner;
public class dfsDouble {
static final int N = 20;
// 记录数据
static int n;
static char[][] arr = new char[N][N];
// 记录行,列,对角线,反对角线
static boolean[] row = new boolean[N];
static boolean[] col = new boolean[N];
static boolean[] dg = new boolean[2*N-1];
static boolean[] udg = new boolean[2*N-1];
// 主函数
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
n = scanner.nextInt();
for (int i = 0;i < n;i++){
for (int j = 0; j < n; j++) {
arr[i][j] = '.';
}
}
dfs(0,0,0);
}
// DFS
private static void dfs(int x,int y,int u) {
// y到头,换行
if(y == n){
y = 0;
x++;
}
// 老规矩判断输出条件
if (x == n){
if (u == n){
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
System.out.print(arr[i][j]);
}
System.out.println();
}
System.out.println();
}
return;
}
// 进行dfs(不选的情况,选该行的其他点位)
dfs(x, y + 1, u);
// 判断是否符合条件
if (!row[x] && !col[y] && !dg[x + y] && !udg[x - y + n])
{
arr[x][y] = 'Q';
row[x] = col[y] = dg[x + y] = udg[x - y + n] = true;
// 进行dfs(符合条件选,继续下一步)
dfs(x, y + 1, u + 1);
row[x] = col[y] = dg[x + y] = udg[x - y + n] = false;
arr[x][y] = '.';
}
}
}
/*升级方法*/
import java.util.Scanner;
public class dfsDouble {
static final int N = 20;
// 记录数据
static int n;
static char[][] arr = new char[N][N];
// 记录列,对角线,反对角线
static boolean[] col = new boolean[N];
static boolean[] dg = new boolean[2*N-1];
static boolean[] udg = new boolean[2*N-1];
// 主函数
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
n = scanner.nextInt();
for (int i = 0;i < n;i++){
for (int j = 0; j < n; j++) {
arr[i][j] = '.';
}
}
dfs(0);
}
// DFS
private static void dfs(int u) {
// 我们采用每行取一个的策略,这里的u就是x
if (u == n){
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
System.out.print(arr[i][j]);
}
System.out.println();
}
System.out.println();
return;
}
// 我们取满足条件的位置
for (int j = 0; j < n; j++) {
if (!col[j] && !dg[u+j] && !udg[u - j + n]){
arr[u][j] = 'Q';
col[j] = dg[u+j] = udg[u-j+n] = true;
dfs(u+1);
col[j] = dg[u+j] = udg[u-j+n] = false;
arr[u][j] = '.';
}
}
}
}
DFS树的重心
我们这里利用DFS来求解一道难题:
- 给定一颗树,树中包含 nn 个结点(编号 1∼n1∼n)和 n−1n−1 条无向边。
- 请你找到树的重心,并输出将重心删除后,剩余各个连通块中点数的最大值。
- 重心定义:重心是指树中的一个结点,如果将这个点删除后,剩余各个连通块中点数的最大值最小,那么这个节点被称为树的重心。
我们给出一个简单示例来表明重心:
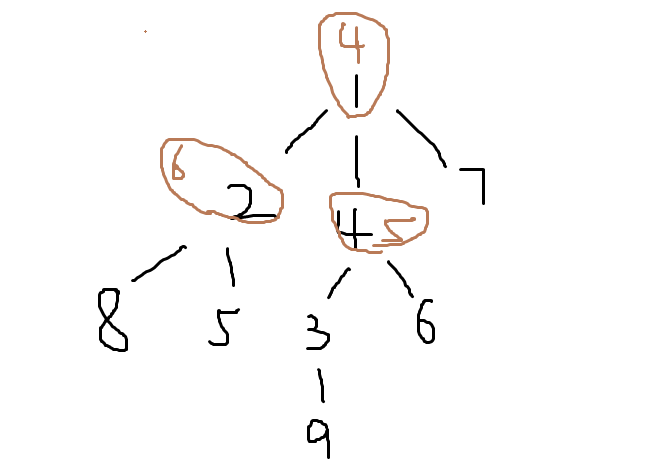
我们来简单介绍一下:
/*输入数据*/
// 第一个是操作次数,然后后面成对书写,表示两者相连
9
1 2
1 7
1 4
2 8
2 5
4 3
3 9
4 6
/*重心介绍*/
我们上图中的黑笔书写部分是由上述数据所搭建出来的无向图,我们上面用树的形式写出
我们的棕笔部分是指去掉该点之后,剩余的联通点分块的个数中的最大块,我们要测试全部的点位,并给出这些最大块的最小快
思路分析:
/*思路分析*/
首先我们要遍历所有的点,一一求解该点删除后的最大块
我们删除该点后,其连通区域主要分为两部分:该点的子点,该点的上一个点的个数去除该点以及该点子类的个数
我们给出相关代码:
import java.util.Scanner;
public class Main {
final static int N = 100010;
// 首先我们用单链表模拟图
static int n;
static int idx;
static int[] h = new int[N];
static int[] e = new int[N*2];
static int[] ne = new int[N*2];
// 判定是否已经经过
static boolean[] isPassed = new boolean[N*2];
// 最大值
static int ans = N;
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
n = scanner.nextInt();
// 将头节点设为-1,方便判断
for (int i = 1; i < N; i++) {
h[i] = -1;
}
// 进行连接
for (int i = 0; i < n-1; i++) {
int a = scanner.nextInt();
int b = scanner.nextInt();
// 注意是无向边,我们需要双向连接
add(a,b);
add(b,a);
}
// 开始遍历
dfsMethod(1);
// 最后输出结果
System.out.println(ans);
}
// dfs操作
private static int dfsMethod(int u) {
// 连通块的最大值
int res = 0;
// 首先将自己设置为已经过点
isPassed[u] = true;
// 该点以及子类的点数(目前已包含自己点)
int sum = 1;
// 开始遍历子点
for (int i = h[u];i != -1;i = ne[i]){
// 将每个点用变量表示出来
int j = e[i];
// 如果该点没有经过,对其dfs遍历
if (!isPassed[j]){
// 遍历时需要返回sum来获得下列点的大小,为了得到ans做准备
int s = dfsMethod(j);
// 和res比较,获得连通块最大值
res = Math.max(res,s);
// 将子类点添加到sum中
sum += s;
}
}
// 我们还需要与抛弃该点后上面的点所产生的res作比较
res = Math.max(res,n-sum);
// 返回最小的ans
ans = Math.min(ans,res);
return sum;
}
// 我们需要一个单链表连接的函数
public static void add(int a,int b){
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
}
BFS走迷宫
我们给出BFS走迷宫题目:
- 给定一个n×m的二维整数数组,用来表示一个迷宫,数组中只包含0或1,其中0表示可以走的路,1表示不可通过的墙壁。
- 最初,有一个人位于左上角 (1,1)处,已知该人每次可以向上、下、左、右任意一个方向移动一个位置。
- 请问,该人从左上角移动至右下角 (n,m)处,至少需要移动多少次。
- 数据保证 (1,1)处和 (n,m)处的数字为0,且一定至少存在一条通路。
问题解析:
/*BFS运作*/
首先我们要知道BFS的运作形式
首先我们BFS是根据距离或长度来进行分类递增
那么在走迷宫时,我们距离为n+1的位置肯定是由距离为n的位置的上下左右方向的位置
那么我们就可以采用一个队列来进行装配,我们将获得的可走的点位和距离保存进去,然后根据这个点位和距离推算下一个点位和距离
我们给出算法代码:
import java.util.Scanner;
public class bfs {
static final int N = 100;
// 存放数据,存放是否使用
static int n,m,hh,tt;
static int[][] arr = new int[N][N];// 地图
static int[][] isPassed = new int[N][N];// 是否经过,若经过修改为距离
static PII[] queue = new PII[N*N];// 队列
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
n = scanner.nextInt();
m = scanner.nextInt();
for (int i=1;i <= n;i++){
for (int j=1;j <= m;j++){
// 输入0/1
arr[i][j] = scanner.nextInt();
// 全部设置为未pass
isPassed[i][j] = -1;
}
}
int res = bfsMethod();
System.out.println(res);
}
private static int bfsMethod() {
// 初始设置
hh = 0 ; tt = -1; //队列的头节点=0,尾节点 = 0;
isPassed[1][1] = 0; // 我们首先站在的是第一个点,所以值距离设置为0
queue[++tt] = new PII(1,1); //然后将第一个点下标存入q队列中
// 提前设置好移动方向(分别对应方向)
int[] xmove = {-1,0,1,0};
int[] ymove = {0,1,0,-1};
// 遍历queue
while (hh <= tt){
PII t = queue[hh++]; //每一次将头结点拿出来
for(int i = 0 ; i < 4 ; i ++ ) {//然后进行下一步要往哪里走,这里可能有多重选择可走
int x = t.x + xmove[i]; //这里进行x轴向量判断
int y = t.y + ymove[i];//这里进行y轴向量的判断
//如果x,y满足在地图中不会越界,然后地图上的点g是0(表示可以走),
//然后这里是没走过的距离d是-1;
if (x > 0 && x <= n && y > 0 && y <= m && arr[x][y] == 0 && isPassed[x][y] == -1) {
//将现在可以走的点(x,y)加上上一个点计数距离的点加上一,就是现在走到的点的距离
isPassed[x][y] = isPassed[t.x][t.y] + 1;
queue[++tt] = new PII(x, y);//然后将这一个可以走的点存入队列尾
}
}
}
return isPassed[n][m]; //最后返回的是地图走到尽头最后一个位置的位置统计的距离
}
//这是一个用来存储两个坐标的类Pair
static class PII{
int x,y;
public PII(int x,int y){
this.x = x;
this.y = y;
}
}
}
BFS八数码
我们给出BFS八数码题目:
- 在一个3×3的网格中,1∼8这 88 个数字和一个
x恰好不重不漏地分布在这 3×3的网格中。 - 在游戏过程中,可以把
x与其上、下、左、右四个方向之一的数字交换(如果存在)。
我们需要将八数码从下列形式变成顺序形式:
/*原八数码*/
1 2 3
x 4 6
7 5 8
/*完善八数码*/
1 2 3
4 5 6
7 8 x
/*变化顺序*/
1 2 3 1 2 3 1 2 3 1 2 3
x 4 6 4 x 6 4 5 6 4 5 6
7 5 8 7 5 8 7 x 8 7 8 x
问题解析:
/*八数码问题解析*/
我们这里要计算最小的移动步数,那么我们就需要采用BFS来计算最近的
其实和之前的走迷宫非常相似,我们将x与上下左右四个方向的数进行对换,然后比较是否为最终结果即可
我们给出算法代码:
import java.util.*;
public class bfs {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
// 开始状况
String start = "";
for(int i = 0 ; i < 9 ; i ++ ){
String s = scanner.next();
start += s;
}
// 结束状况
String end = "12345678x";
// bfs循环
System.out.println(bfsMethod(start,end));
}
public static int bfsMethod(String start,String end){
// 哈希表存放字符串和对应的移动步数
HashMap<String,Integer> hashMap = new HashMap<String, Integer>();
// 队列存放字符串
Queue<String> queue = new LinkedList<>();
// 存放第一个点(还未开始,启动步数为0)
hashMap.put(start,0);
queue.add(start);
while (!queue.isEmpty()){
// 将head数据拿出来
String s = queue.poll();
// 首先判断是否符合条件
if (s.equals(end)) return hashMap.get(s);
// 找到x坐标
int index = s.indexOf("x");
// 计算对应位置
int x = index/3;
int y = index%3;
// 然后上下左右移动判断
int[] xmove = {1,0,-1,0};
int[] ymove = {0,1,0,-1};
for (int i=0;i<4;i++){
int a = x + xmove[i];
int b = y + ymove[i];
//如果这种情况没有超出边界
if(a >= 0 && a < 3 && b >= 0 && b < 3){
//将这种情况的字符串转化成字符数组,能够有下标进行交换
char[] arr = s.toCharArray();
//然后交换x跟没有超出边界的值进行交换,二维转成一维下标x*3+y;
swap(arr, index, a * 3 + b);
//然后将字符数组转化成字符串
String str = new String(arr);
//如果这种情况对应的value值是null,说明还没有走过
if(hashMap.get(str) == null){
//然后将这种情况对应进行上一步的距离加上1
hashMap.put(str,hashMap.get(s) + 1);
//然后将新的情况插入到队尾中
queue.offer(str);
}
}
}
}
return -1;
}
// 交换算法
public static void swap(char[] arr,int x,int y){
char temp = arr[x];
arr[x] = arr[y];
arr[y] = temp;
}
}
BFS图层次
我们这里利用BFS来求解一道难题:
- 给定一个n个点m条边的有向图,图中可能存在重边和自环。
- 所有边的长度都是1,点的编号为1∼n。
- 请你求出1号点到n号点的最短距离,如果从1号点无法走到n号点,输出 −1。
我们采用BFS来逐层递进,其原理其实和前面两道题相同:
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;
public class bfsssss {
final static int N = 100010;
// 单链表模拟图
static int n,m;
static int hh,tt;
static int idx;
static int[] h = new int[N];
static int[] e = new int[N];
static int[] ne = new int[N];
// 距离存储以及队列
static int[] distance = new int[N];
static int[] queue = new int[N];
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
n = scanner.nextInt();
m = scanner.nextInt();
// 初始化
for (int i = 1; i < N; i++) {
h[i] = -1;
distance[i] = -1;
}
// 赋值
for (int i = 0;i < m;i++ ){
int a = scanner.nextInt();
int b = scanner.nextInt();
add(a,b);
}
// BFS操作
int res = bfsFind();
// 输出
System.out.println(res);
}
// bfs操作
public static int bfsFind(){
// 设置hh,tt
hh = 0;
tt = -1;
// 第一个点距离为0
distance[1] = 0;
// 将第一个点加入队列
queue[++tt] = 1;
// 开始队列循环
while (hh <= tt){
int t = queue[hh++];
// 取得该点,对其ne进行处理
for (int i = h[t]; i != -1; i = ne[i]) {
// 得到该子点,进行处理
int s = e[i];
if (distance[s] == -1){
// 如果没有经过就设置dis,并且加入队列
distance[s] = distance[t] + 1;
queue[++tt] = s;
}
}
}
return distance[n];
}
// 经典单链表添加方法
public static void add(int a,int b){
e[idx] = b;
ne[idx] = h[a];
h[a] = idx;
idx++;
}
}
结束语
好的,关于搜索与图论篇的DFS和BFS算法就介绍到这里,希望能为你带来帮助~




