图卷积网络 GCN

转载自梦家博客

研究背景

首先，为什么需要研究图卷积网络GCN（Graph Convolution Network）呢？

目前算法研究处理的数据主要分为两种：

• Euclidean 结构数据：主要有图片、语音、文本等数据结构，例如图像、视频中像素点是排列整齐的矩阵，可以被CNN(Convolution Neural Network)高效地处理。

• Non-Euclidean 结构数据：主要有图（graph）和三维几何等数据，CNN 无法直接处理在这些数据。

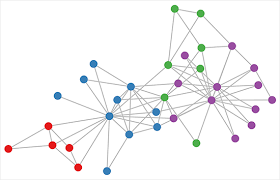
因此，研究 GCN 的原因可以分为以下三点：

1. CNN 无法直接处理 Non-Euclidean 数据。学术表达是传统离散卷积无法在 Non-Euclidean 的结构数据上无法保持平移不变性；简而言之就是在图结构数据中每个顶点的邻居节点数据不同，无法使用相同大小的卷积核来进行卷积运算。
2. 由于 CNN 无法直接处理 Non-Euclidean 结构数据，而卷积操作可以有效地提取数据的特征。因此，如何在图数据中利用卷积来提取空间特征来进行机器学习是一个亟待解决的问题，也是 GCN 研究的重点内容。
3. 如果研究的问题本身不具备拓扑图结构，是否可以使用 GCN？广义上来说任何数据在其空间内都可以建立拓扑关联，例如谱聚类方法（谱聚类原理总结），因此拓扑图结构是一种广义的数据结构，GCN 可以应用在多个领域当中。

回顾 CNN

CNN 比 FC 有效且在在图像识别等任务中取得显著的成效，主要是因为 CNN 的以下特性：

• 局部平移不变性（Local Translational Invariance）
• 卷积核特性（Convolution Kernels）
  • 参数共享（Parameter Sharing）
  • 局部连接性（Local Connection）
• 层次化表达（Hierarchical Expression）

局部平移不变性

对于 CNN 而言，其核心在于使用了基于卷积核的卷积操作来提取图像的特征，即计算区域内的中心节点和相邻节点进行加权求和。

CNN 在图像领域取得显著效果的原因是图片（RGB）是规则化的数据结构，可存储在三维矩阵中，无论卷积核平移到图片中的哪个位置都可以保证其运算结果的一致性，这就是局部平移不变性。如下图所示：

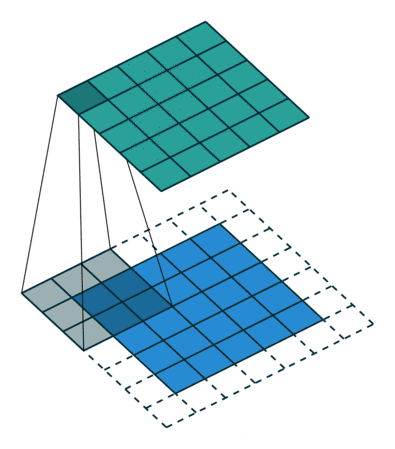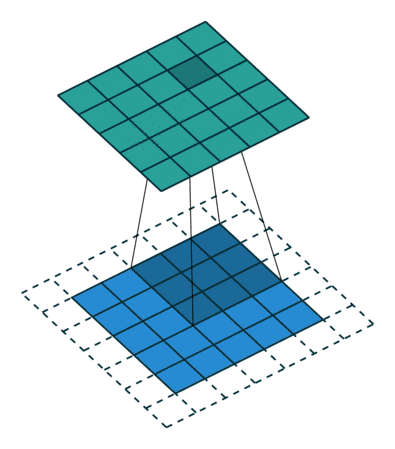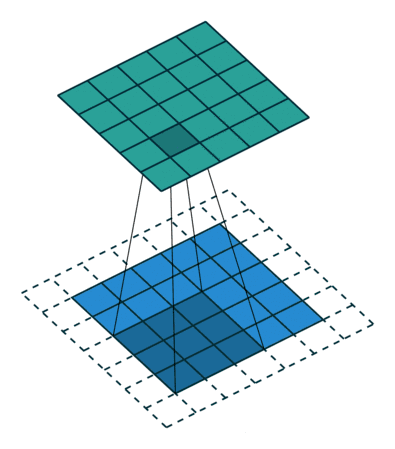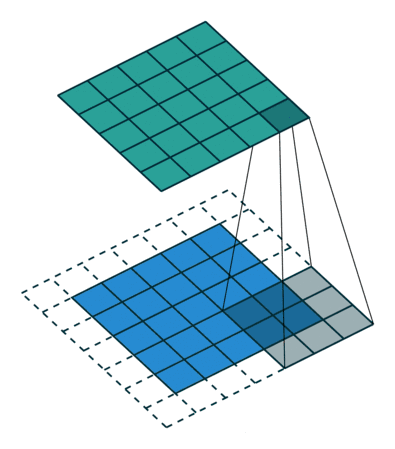
CNN 的卷积本质就是利用这种平移不变性来对扫描的区域进行卷积操作，从而实现图像特征的提取。

拓扑图结构是不规则的数据结构，所以其不存在平移不变形（每个顶点的周围邻居数不固定），如下图所示，无法使用固定大小的卷积核来进行卷积操作，使得传统的 CNN 方法无法直接应用于网络中。

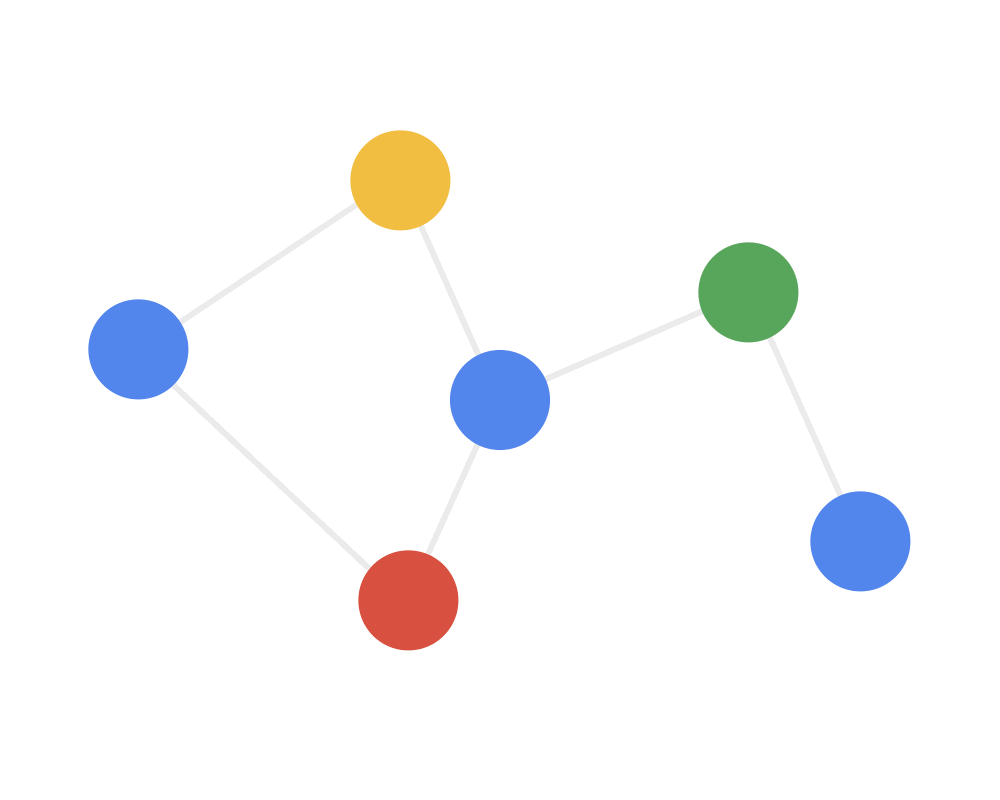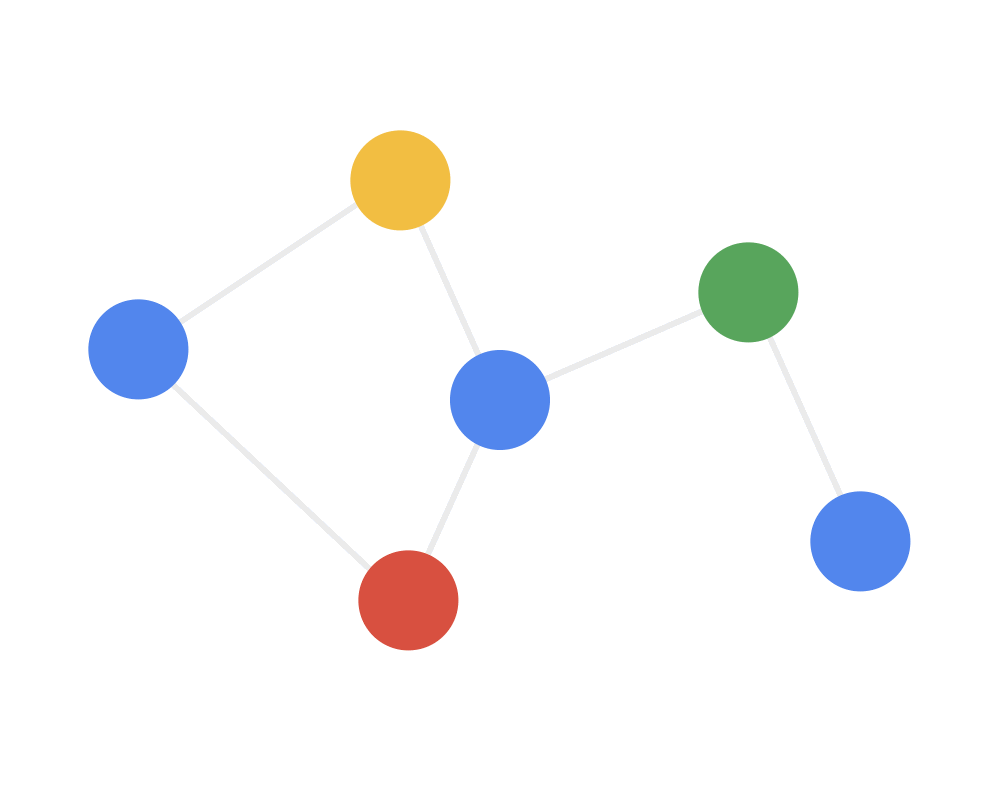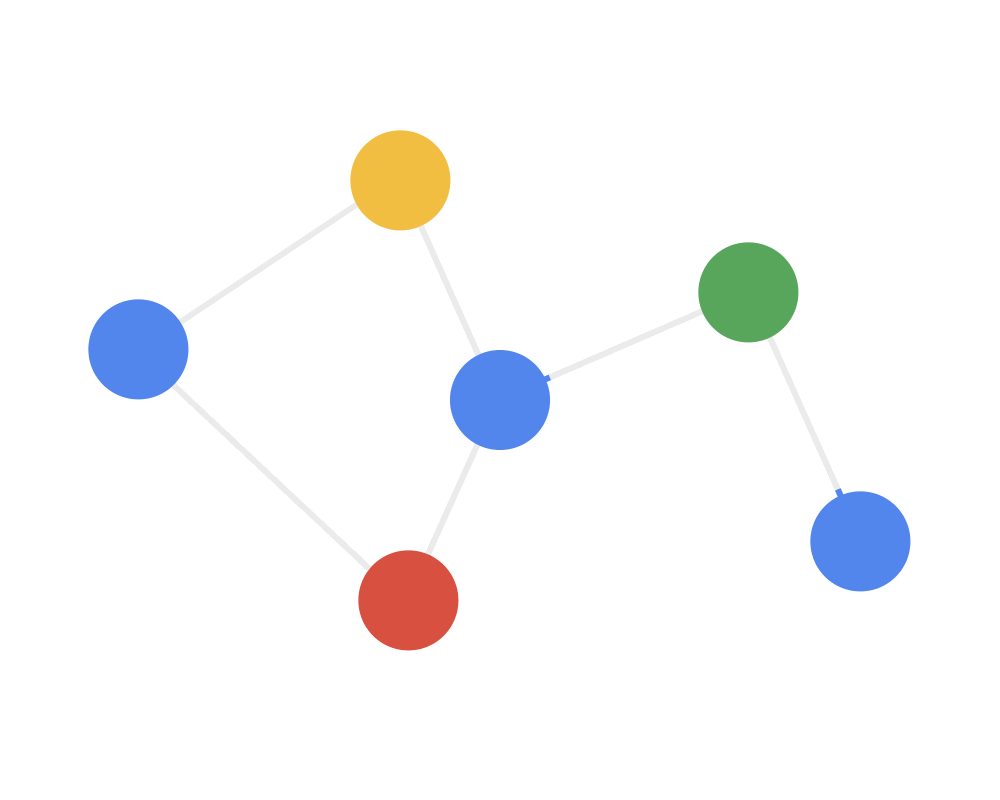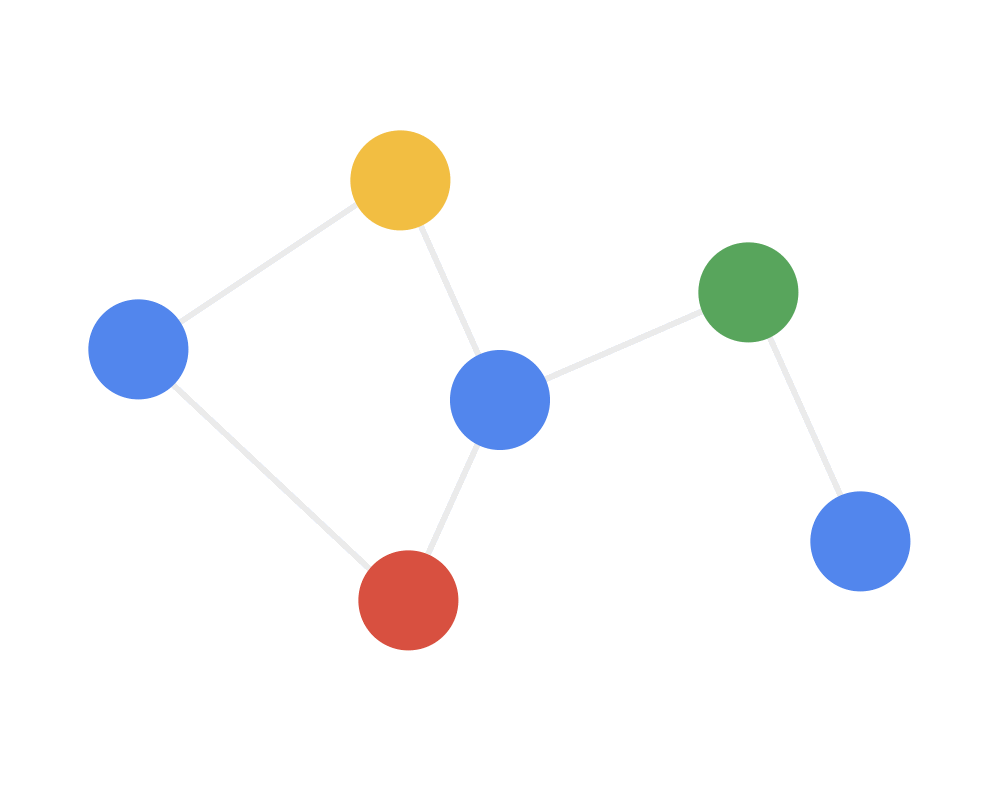
卷积核特性

CNN 一个核心的思想是卷积核参数共享（Parameter Sharing），卷积核在图像上的卷积操作如下：

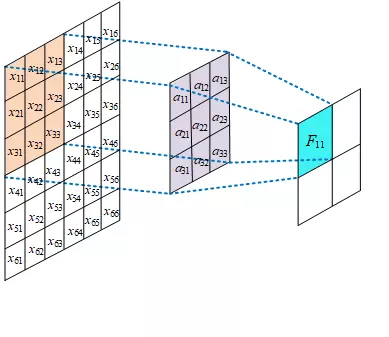
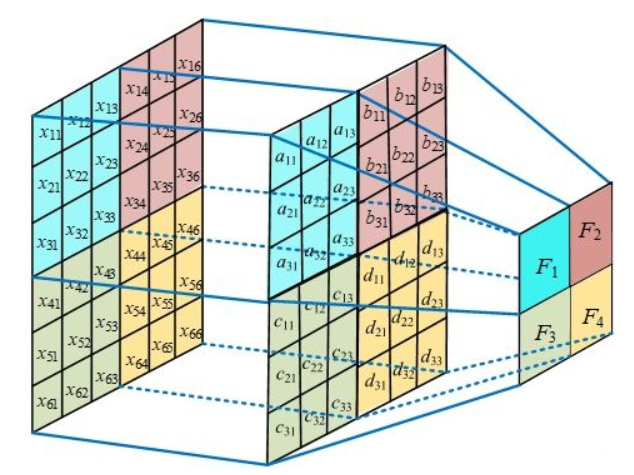
此时模型的参数大小仅与卷积核大小有关，而如果不进行参数共享的话，参数的大小则与图像的像素矩阵保持一致，如下图所示：

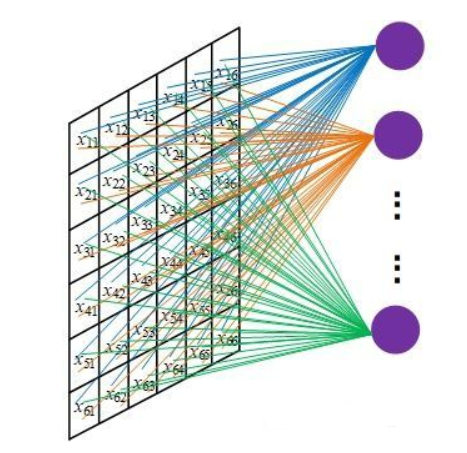
CNN 另一核心思想是卷积核的局部连接性（Locally Connection），局部连接是指卷积操作仅在与卷积核大小对应的区域进行，卷积操作的输入和输出是局部连接的，全局连接则会导致模型参数量巨大，与 FC（Full Connection）网络类似：

PS：卷积核还有另一特性，每个卷积核都是\(O(1)\)复杂度，与输入大小无关。这样可以提高模型的泛化能力。

层次化表达

CNN 的层次化表达是指神经网络通过多个卷积层对图片进行特征提取，包括池化（Pooling）操作。每一个卷积层在前一层的基础上进行处理操作，那么随着网络深度的增加，其提取到的特征越高级，趋于语义特征。比如说：第一层可能是一些线条，第二层可能会是一些纹理，第三层可能是一些抽象图案，如下图所示：

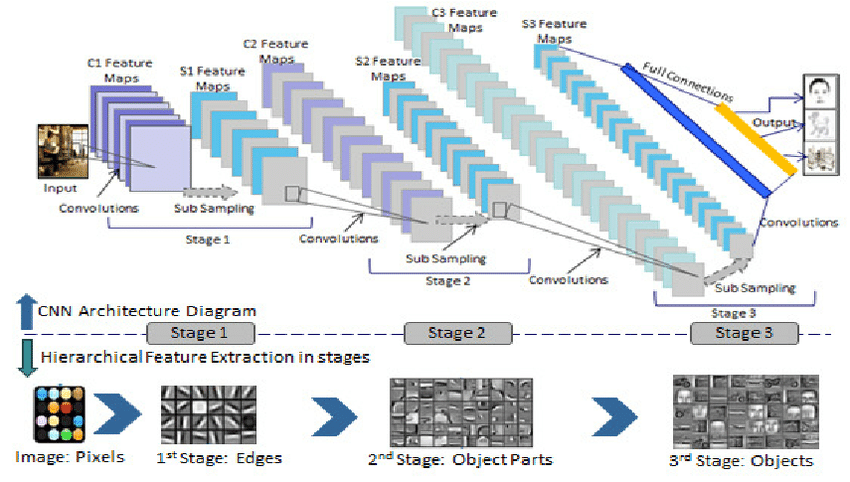
用卷积提取Graph空间特征

现在常用的图卷积可以被分成两类：

• 空域卷积（vertex domain、spatial convolution）
• 频域卷积/谱图卷积（spectral domain）

空域图卷积直接在原空间图上做卷积运算。频域图卷积是先把信号转换到傅立叶空间，然后做卷积运算后再转换到原始空间。

空域卷积

上述谈到 CNN 难以应用在图上的问题在于顶点的邻域无法确定，空域卷积是以最直观的方式选择特定数量的领域并在每个节点及其领域组成的矩阵中进行卷积运算。经典空域卷积文章推荐阅读：Learning Convolutional Neural Networks for Graphs

这篇文章针对图分类任务，过程如下图所示：

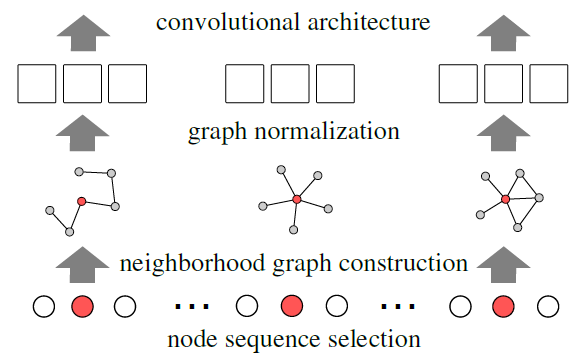
算法步骤如下：

1. 根据中心性的方法选择\(w\)个可以代表 graph 的顶点——即计算顶点与其它所有节点的距离和，和值越小说明该顶点的中心性越大。
2. 为每个顶点找到\(K\)个邻域顶点。先从一阶邻域中选择，如果顶点数大于\(K\)那么删除中心性值小的顶点；如果顶点数小于\(K\)那么接着从二阶邻域中选择或者补充\(0\)向量。
3. 选出的K个节点，每个节点和其它节点可以构成 \((K+1)\times F\)的矩阵，所有的边也可以构成\((K+1) \times (K+1) \times F\)的张量，然后在这些张量中做卷积操作。

这种方法的缺点如下：

• 每个顶点的邻域顶点都不相同，使得计算处理必须针对每个节点；
• 图的空间特征提取效果不好；

以上简单阐述了空间域图卷积的方法，如果对该思路有兴趣可以查阅相关资料。

接下来准备介绍谱图理论和图上的傅里叶变换、逆变换！

频域（谱图）卷积

如要了解谱图卷积，首先需要学习图理论基础和图中如何进行傅里叶变换。

对于傅里叶变换，本文不再赘述。详细内容可以参考：

• 理解傅里叶变换    深入理解傅里叶变换

图上的傅立叶变换

傅立叶变换是将时域的函数转换成频域上的函数，是对于同一个函数的不同视角，数学定义如下：

\[\mathcal{F}(w)=\mathcal{F}(f(t))=\int{f(t)e^{-iwt}}dt \tag{1} \label{flybh} \]

公式\(\eqref{flybh}\)表示的意义是傅立叶变换是时域信号\(f(t)\)与基函数\(e^{-iwt}\)的积分。

为什么选择\(e^{-iwt}\)作为基函数？原因有二：

• \(e^{-iwt}\)是正交函数系。
• \(e^{-iwt}\)是拉普拉斯算子\(\Delta\)的特征函数。

至于\(e^{-iwt}\)由何种推导得来的请参考： 理解傅里叶变换

拉普拉斯算子\(\Delta\)定义

在数学中，拉普拉斯算子（Laplacian）是由欧几里得空间中的一个函数的梯度的散度给出的微分算子，记为\(\Delta f=\nabla^{2} f=\nabla \cdot \nabla f\)，表示n维空间笛卡尔坐标系\(x_i\)​中所有非混合二阶偏导数之和，其数学定义为

\[\Delta=\sum_{i=1}^n\frac{\partial^2}{\partial{^2x_{i}}} \tag{2} \label{lplssz} \]

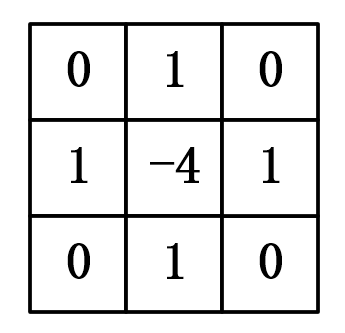
以二维空间为例，上述二阶偏导退化为具有4个方向的差分形式：

\[\begin{aligned} \Delta f(x, y) &=\frac{\partial^{2} f}{\partial x^{2}}+\frac{\partial^{2} f}{\partial y^{2}} \\ &=[f(x+1, y)+f(x-1, y)-2 f(x, y)]+[f(x, y+1)+f(x, y-1)-2 f(x, y)] \\ &=f(x+1, y)+f(x-1, y)+f(x, y+1)+f(x, y-1)-4 f(x, y) \end{aligned} \]

上式中每一项的系数就是拉普拉斯在二维图像中的卷积核：

拉普拉斯算子\(\Delta\)的特征函数（\(e^{-iwt}\)）

拉普拉斯算子的特征方程为：

\[\Delta g=\lambda g \tag{3} \label{lplstzfc} \]

其中\(\Delta\)是离散拉普拉斯算子，\(g\)是特征向量或者特征函数（可以认为是无限维的特征向量）， \(\lambda\)是特征值。

由于\(e^{-iwt}\)是拉普拉斯算子的特征函数，将\(g=e^{-iwt}\)代入上式可得：

\[\Delta e^{-iwt}=\frac{\partial^2}{\partial^2 t}e^{-iwt}=-w^2 e^{-iwt} \tag{4} \label{lplstzfc1} \]

其中特征值\(\lambda=-w^2\)，即\(w\)和特征值\(\lambda\)密切相关。

由上述证明可得结论：傅立叶变换是时域信号与拉普拉斯算子特征函数的积分。

从整体推特殊，将以上的结论推广到（离散）图中可知：图上的傅立叶变换就是时域信号与图拉普拉斯算子特征函数的求和。

对于傅里叶变换式\(\eqref{flybh}\)，将特征函数转换为特征向量（特征函数可以认为是无限维的特征向量），将积分转换为求和，那么N个顶点图上的傅立叶变换表达式为：

\[\mathcal{F}(\lambda_l)=\widehat f(\lambda_l)=\sum_{i=1}^N f(i)*u_l(i) \tag{5} \label{syflybh} \]

其中，\(\lambda_l\) 为图拉普拉斯算子第\(l\)个特征值，\(f\)是Graph上的\(N\)维向量，\(f(i)\)是Graph上的顶点一一对应，\(u_{l}\) 为第\(l\)个特征值对应的特征向量。那么\(f\)的Graph上的傅里叶变换就是与特征值（频率）\(\lambda_l\)对应的特征向量\(u_{l}\)进行内积运算。

对于图拉普拉斯算子，具有N个特征值，将式\(\eqref{syflybh}\)全部分量展开可得：

\[\left(\begin{array}{c} \hat{f}\left(\lambda_{1}\right) \\ \hat{f}\left(\lambda_{2}\right) \\ \vdots \\ \hat{f}\left(\lambda_{N}\right) \end{array}\right) =\left(\begin{array}{cccc} u_{1}(1) & u_{1}(2) & \dots & u_{1}(N) \\ u_{2}(1) & u_{2}(2) & \dots & u_{2}(N) \\ \vdots & \vdots & \ddots & \vdots \\ u_{N}(1) & u_{N}(2) & \dots & u_{N}(N) \end{array}\right) \left(\begin{array}{c} f(1) \\ f(2) \\ \vdots \\ f(N) \end{array}\right) \tag{6} \label{syflybhzk} \]

将公式\(\eqref{syflybhzk}\)写成矩阵形式即为：

\[\widehat f=U^{T}f \tag{7} \label{syflybhjz} \]

此处\(U\)为拉普拉斯谱分解的正交矩阵。

最后再来看看图中拉普拉斯算子的定义：

\[L=D-W \tag{8} \label{tlslssz} \]

其中\(W\)是邻接矩阵，\(D\)是度矩阵，\(D_{i,i}\)​等于\(W\)矩阵的第\(i\)行的和，非对角线上元素为0，\(D\)是个对角矩阵，这个图谱理论关于图拉普拉斯算子的的定义。详细推到过程参考：图拉普拉斯算子为何定义为 D-W

拉普拉斯矩阵是实对称矩阵，实对称矩阵一定可以用正交矩阵进行正交相似对角化（特征分解）：

\[L=U\left(\begin{array}{ccc} \lambda_{1} & & \\ & \ddots & \\ & & \lambda_{N} \end{array}\right) U^{-1} =U\left(\begin{array}{ccc} \lambda_{1} & & \\ & \ddots & \\ & & \lambda_{N} \end{array}\right) U^{T} \tag{9} \label{lplsjztzfj} \]

\(U\)为特征向量构成的正交矩阵，而正交矩阵的逆等于正交矩阵的转置：\(U^{-1}=U^T\)

假定\(\lambda_{1},\cdots,\lambda_{n}\)​ 从小到大排序，其对应的特征向量为\(u_1,\cdots, u_n\)，特征值越小，对应的特征向量越平稳，这和傅立叶变换中频率的定义是类似的。

图上傅里叶逆变换

有了傅立叶变换，如何将频率函数变换为时域函数呢？这是傅立叶逆变换需要干的事情，公式如下：

\[\mathcal{F}^{-1}[\mathcal{F}(w)]=\frac{1}{2\pi}\int \mathcal{F}(w)e^{-iwt}dw \tag{10} \label{flynbh} \]

公式\(\eqref{flynbh}\)和公式\(\eqref{flybh}\)类似，差一个常数系数。公式\(\eqref{flybh}\)积分之后是一个关于\(w\)的函数，公式\(\eqref{flynbh}\)对\(w\)积分后是关于\(t\)的函数，从频域变换到了时域，图上傅立叶变换类似为：

\[\left(\begin{array}{c} f\left(\lambda_{1}\right) \\ f\left(\lambda_{2}\right) \\ \cdots \\ f\left(\lambda_{N}\right) \end{array}\right)=\left(\begin{array}{cccc} u_{1}(1) & u_{1}(2) & \dots & u_{1}(N) \\ \cdots & \dots & & \dots \\ u_{1}(1) & u_{1}(2) & \dots & u_{1}(N) \end{array}\right)\left(\begin{array}{c} \hat{f}\left(\lambda_{1}\right) \\ \hat{f}\left(\lambda_{2}\right) \\ \dots \\ \hat{f}\left(\lambda_{N}\right) \end{array}\right) \tag{11} \label{tflynbh} \]

写成矩阵形式：

\[f=\mathbf{U} \mathbf{U}^{-1} f=\mathbf{U} \mathbf{U}^{T} f=\mathbf{U} \hat{f} \tag{12} \label{tflynbhjz} \]

上述内容详述了如何在图中进行傅里叶变换和逆变换，下面说说图卷积网络 GCN。

图卷积

卷积定义：在泛函分析中，卷积是通过两个函数\(f\)和\(g\)生成第三个函数的一种数学算子，表示函数\(f\)与经过翻转和平移的\(g\)的乘积函数所围成的曲边梯形的面积，公式如下所示：

\[(f*g)(t) \stackrel{\text { def }}{=} \int_{\mathbb{R}^{n}} f(\tau) g(t-\tau) d \tau \tag{13} \label{jj} \]

下面给出两幅图来直观理解上述公式，参考 卷积解释：

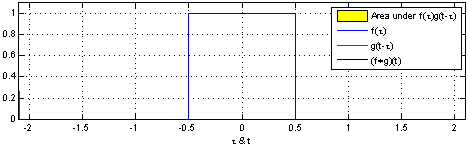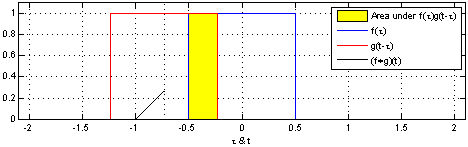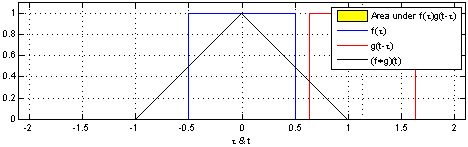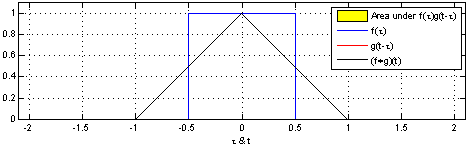
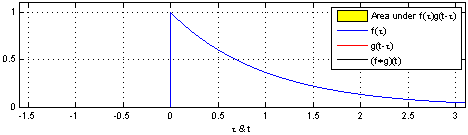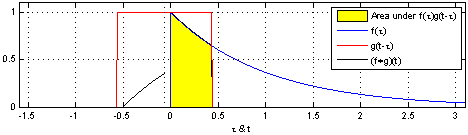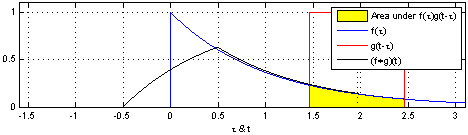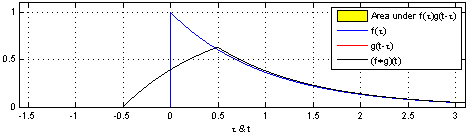
以上是连续函数的卷积运算，对于离散卷积公式定义如下：

\[(f*g)[n]=\sum_{m=-\infty}^{\infty} f[m] g[n-m]=\sum_{m=-\infty}^{\infty} f[n-m] g[m] \tag{14} \label{lsjj} \]

卷积除了直接计算这种方法，还可以根据卷积定理来计算。

卷积定理：在适当条件下，两个信号的卷积的傅立叶变换等于它们傅立叶变换的点积。例如，一个域（如时域）的卷积等于另一个域（如频域）的点乘：

\[\mathcal{F}\{f*g\}=\mathcal{F}\{f\} \cdot \mathcal{F}\{g\} \tag{15} \label{flybhdc} \]

如果以\(\mathcal{F}^{-1}\)表示傅立叶逆变换，那么卷积计算可以重新表示为：

\[f*g=\mathcal{F}^{-1}\{\mathcal{F}\{f\} \cdot \mathcal{F}\{g\}\} \tag{16} \label{flybhjj} \]

PS：利用卷积定理可以简化卷积的运算量。对于一个长度为 n 的序列，按照卷积的定义来计算则需要做\(2n-1\)组对位乘法，即时间复杂度为\(O(n^2)\)；而利用傅立叶变换后，只需要计算一组对位乘法，而且离散傅立叶变换有快速的算法（快速傅立叶变换），所以总的计算复杂度为\(O(n\log n)\)。

谱图卷积思想：既然无法直接在空域对图进行卷积，那么将图信号映射到频域后再做卷积操作。

根据公式\(\eqref{flybhjj}\)与\(\eqref{syflybhjz}\)，可得

\[\begin{aligned} (f*h)_{G} =\mathcal{F}^{-1}[\mathcal{F}\{f\} \cdot \mathcal{F}\{h\}]=\mathcal{F}^{-1}\left[\mathbf{U}^{T} f \cdot \hat{h}\right] \end{aligned} \tag{17} \label{flybhjj1} \]

上式表示时域信号\(f\)和\(h\)的卷积等价于将信号转换到傅立叶域做点乘后再逆变换回来。其中，向量\(f\)与向量\(\hat{h}\)的元素点积，等价于将\(\hat{h}\)组织成对角矩阵的形式进行矩阵乘法，可得：

\[\begin{aligned} (f*h)_{G} =\mathcal{F}^{-1}\left[\mathbf{U}^{T} f \cdot \hat{h}\right]=\mathcal{F}^{-1}\left[\operatorname{diag}\left[\hat{h}_{1}, \ldots, \hat{h}_{n}\right] \mathbf{U}^{T} f\right] \end{aligned} \tag{18} \label{flybhjj2} \]

根据图上的傅立叶逆变换计算公式，上式可重写为：

\[(f * h)_{G}=\mathbf{U} \operatorname{diag}\left[\hat{h}_{1}, \ldots, \hat{h}_{n}\right] \mathbf{U}^{T} f \tag{19} \label{flybhjj3} \]

也可以写成写成矩阵形式为：

\[(f*h)_G=\mathbf{U} ((\mathbf{U} ^Tf) \odot (\mathbf{U} ^Th)) \tag{20} \label{flybhjj4} \]

其中\(\odot\)表示Hadamard积，对于两个维度相同的向量、矩阵、张量进行对应位置的逐元素乘积运算。
目前先不写成式\(\eqref{flybhjj4}\)的形式，是因为在 GCN 中我们的卷积核是可训练并且参数共享的，所以在此我们可以直接令

\[\operatorname{diag}\left[\hat{h}_{1}, \ldots, \hat{h}_{n}\right] =\operatorname{diag}\left[\theta_{1}, \ldots, \theta_{n}\right] = g_{\theta} \tag{21} \label{cshg} \]

这就是深度学习中的可学习参数。

图卷积

论文来源：《Spectral Networks and Deep Locally Connected Networks on Graphs》

第一代图卷积的计算方法就直接根据式\(\eqref{flybhjj3},\eqref{cshg}\)推出

\[y=\sigma\left(\mathbf{U} g_{\theta} \mathbf{U}^{T} x\right)=\sigma\left(\mathbf{U}\left[ \begin{array}{cccc} \theta_{1} & & & \\ & \theta_{2} & & \\ & & \ddots & \\ & & & \theta_{N} \end{array} \right] \mathbf{U}^{T} x \right) \tag{22} \label{1gcn1} \]

虽然利用上式已经可以构造深度网络进行图卷积运算了，但该版本有不少缺点：

1. 没有 local 信息。每次卷积都是所有顶点都参与运算，没有实现局部卷积和参数共享。
2. 运算量大。每次卷积都要进行拉普拉斯矩阵分解和矩阵相乘，计算复杂度为\(O(N^3)\)。
3. 参数量大。每个卷积核参数量为\(O(N)\)。

图卷积改进一（Fast Localized Spectral Filtering）

针对上述的谱卷积中存在的问题, 于是有了利用切比雪夫多项式(Chebyshev polynomials)进行多项式插值逼近的改进版，即《Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering》

首先回顾下图傅里叶计算公式：

\[\mathcal{F}_{T}\left(\lambda_{k}\right)=\hat{g}_{k}=\sum_{i=1}^{N} g(i) u_{k}(i) \tag{23} \label{2gcn1} \]

可知函数和特征值密切相关，令\(g_{\theta}\)为拉普拉斯矩阵\(L\)的特征值函数\(g_{\theta}(\Lambda)\)：

\[y=\sigma\left(\mathbf{U} g_{\theta} \mathbf{U}^{T} x\right)=\sigma\left(\mathbf{U} g_{\theta}(\Lambda) \mathbf{U}^{T} x\right) \tag{24} \label{2gcn2} \]

以拉普拉斯矩阵的特征值作为卷积核同样存在缺陷：

• 不具备局部连接性；
• 时间复杂度为\(O(n)\);

为了克服上述缺陷引入K阶多项式：

\[g_{\theta}(\Lambda) \approx \sum_{k=0}^{K-1} \theta_{k} \Lambda^{k} \tag{25} \label{2gcn3} \]

其中，参数\(\theta_k\in R^K\)是多项式系数，因此滤波器具有了K阶局部性，复杂度也降低到\(O(K)\)。

将式\(\eqref{2gcn3}\)代入图卷积式\(\eqref{1gcn1}\)中可得：

\[y=\sigma\left(\mathbf{U} g_{\theta}(\Lambda) \mathbf{U}^{T} x\right)=\sigma\left(\mathbf{U} \sum_{k=0}^{K-1} \theta_{k} \Lambda^{k} \mathbf{U}^{T} x\right)=\sigma\left(\sum_{k=0}^{K-1} \theta_{k} L^{k} x\right) \tag{26} \label{2gcn4} \]

其中\(\sigma\)是激活函数，公式\(\eqref{2gcn4}\)的计算时间复杂度为\(O(K×N^2)\)，因为对于静态图而言\(L\)是固定的，\(L^k\)可以提前计算得到。如果使用稀疏矩阵乘法（pytorch 里有封装），时间复杂度是\(O(K×\|E\|)\)。其中\(\|E\|\)是稀疏矩阵中非零元的个数表示图中边的数量。 此时计算图卷积就不需要再乘上特征向量矩阵\(\mathbf{U}\)，而是直接使用拉普拉斯矩阵\(L\)的k次方，就避免了进行特征分解。

因为\(L^k\)当\(K\)很大的时候并不稀疏（\(\|E\|\)接近\(N^2\)），所以文中提出了利用切比雪夫多项式展开（任何k次多项式都可以通过切比雪夫多项式展开）来近似\(L^k\)，切比雪夫多项式递归式为：

\[\begin{aligned} T_0(x)&=1\\ T_1(x)&=x\\ T_k(x)&=2xT_{k-1}(x)-T_{k-2}(x) \end{aligned} \tag{27} \label{2gcn5} \]

因此根据上式可知：

\[g_{\theta}(\Lambda) \approx \sum_{k=0}^{K-1} \theta_{k} T_{k}(\widetilde{\Lambda}) \tag{28} \label{2gcn6} \]

其中，\(\tilde{\Lambda}=\frac{2}{\lambda_{\max }} \Lambda-I_{N}\)​;\(\lambda_{\max}\)是指拉普拉斯矩阵\(L\)的最大特征值。

PS：因为切比雪夫多项式的输入要在[−1,1]之间，由于拉普拉斯矩阵的半正定性，所以所有的特征值都是大于等于 0 的，将其除以最大特征值可以将特征压缩到[0,1] 区间内，现在需要将其压缩到[-1, 1]，所以我们有：\(\tilde{\Lambda}=\frac{2}{\lambda_{\max }} \Lambda-I_{N}\)​。

我们将切比雪夫多项式引入到我们的卷积变换中：

\[g_{\theta} * x \approx \sum_{k=0}^{K-1} \theta_{k} T_{k}(\widetilde{L}) x \tag{29} \label{2gcn7} \]

其中，\(\tilde{L}=\frac{2}{\lambda_{\max }} L-I_{N}\) 。这个表达式为拉普拉斯多项式中的一个k阶近似函数，依赖于节点的k阶邻域（k步可达），时间复杂度与边呈线形相关。

总结，该图卷积改进版优点如下：

• 运算量相比原来图卷积的\(O(N^3)\)可以降到\(O(K\|E\|)\)。
• 引入 K-hop 感受野，可以捕捉局部特征。

图卷积改进二（Layer-wise Linear model）

上述图卷积改进版解决了拉普拉斯矩阵特征分解的问题，但是在计算图卷积操作时矩阵乘法时间复杂度为\(O(N^2)\)，在此基础上优化 Kipf 等人提出了目前流行的GCN，即《Semi-supervised Classification with Graph Convolutional Networks》。

GCN 通过式\(\eqref{2gcn7}\)进行多层卷积层进行叠加，而每层都会逐点进行非线性叠加。考虑到时间复杂度问题，令\(K=2\)，也就是说得到了一个拉普拉斯算子的二阶近似函数。既可以对网络进行卷积操作计算量增加不大。通过叠加层数可以提升模型的非线性。

归一化的拉普拉斯矩阵的特征值区间为[0,2]，令\({\lambda}_{max} \approx 2, K=2\)可得：

\[g_{\theta} * x \approx \theta_{0} x+\theta_{1}\left(L-I_{N}\right) x=\theta_{0} x-\theta_{1} D^{-\frac{1}{2}} A D^{-\frac{1}{2}} x \tag{30} \label{3gcn1} \]

其中，\(\theta_0,\theta_1\)​是切比雪夫系数且仅存的两个参数！

在 GCN 的训练过程中需要规范化参数避免过拟合，令\(\theta_{0}^{\prime}=-\theta_{1}^{\prime}\)，由式可得：

\[g_{\theta} * x \approx \theta\left(I_{N}+D^{-\frac{1}{2}} A D^{-\frac{1}{2}}\right) x \tag{31} \label{3gcn2} \]

注意\(I_{N}+D^{-\frac{1}{2}} A D^{-\frac{1}{2}}\)​的特征值范围在[0, 2]之间，所以如果在很深的网络中会引起梯度爆炸的问题，需要再次进行一次归一化（Renormalization trick）：

\[I_{N}+D^{-\frac{1}{2}} A D^{-\frac{1}{2}} \rightarrow \tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}} , \tilde{D}_{i i}=\sum_{j} \tilde{A}_{i j} \tilde{A}=A+I_{N} \tag{32} \label{3gcn3} \]

把上式从标量推广到矩阵，对于输入顶点的向量\(X \in R^{N \times C}\)，其中N为节点数，C为顶点的特征向量维度，可得：

\[Z=\tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}} X \Theta \tag{33} \label{3gcn4} \]

其中，\(\Theta \in R^{C \times F}\)是参数矩阵，\(Z \in R^{N \times F}\)是卷积后的顶点特征，时间复杂度为\(O(\|E\|FC)\)。

根据上式一层卷积，多层图卷积计算公式公式为：

\[H^{(l+1)}=\sigma\left(\tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}} H^{(l)} W^{(l)}\right) \tag{34} \label{3gcn5} \]

其中，\(\tilde{A}=A+I_N\)，\(A\)为邻接矩阵，\(I_N\)为单位矩阵，所以\(\tilde{A}\)为添加自连接的邻接矩阵；\(\tilde{D}_{ii}=\sum_{j}\tilde{A}_{ij}\),

\(\tilde{D}\)为顶点的度数矩阵；\(W^{(l)}\)为神经网络第\(l\)层的权重矩阵；\(\sigma(\cdot)\)是激活函数；\(H^{(1)} \in R^{N \times D}\)是第\(l\)层的激活矩阵，并且\(H^{(0)}=X\)，\(X\)是由顶点的特征向量组成矩阵。

总结图卷积改进二：

• 令 K=1，相当于只考虑 1-hop 邻点。通过堆叠层数来增加感受野。
• 每层计算复杂度降低为\(O(\|E\|)\)。

总结：CNN 中的卷积无法直接应用于网络图中，所以引出了谱图理论和图中的傅里叶变换，进而定义图卷积的计算方法，最后结合深度学习发展出来 GCN。