北航软院人工智能课程笔记
你软绝世好课,实际上照搬浙大吴飞老师(慕课)&台大李宏毅老师(B站or油管)的PPT……
上课听不进去可以直接去听这两位老师的课。
期末复习自用笔记,有误欢迎指正。
绪论
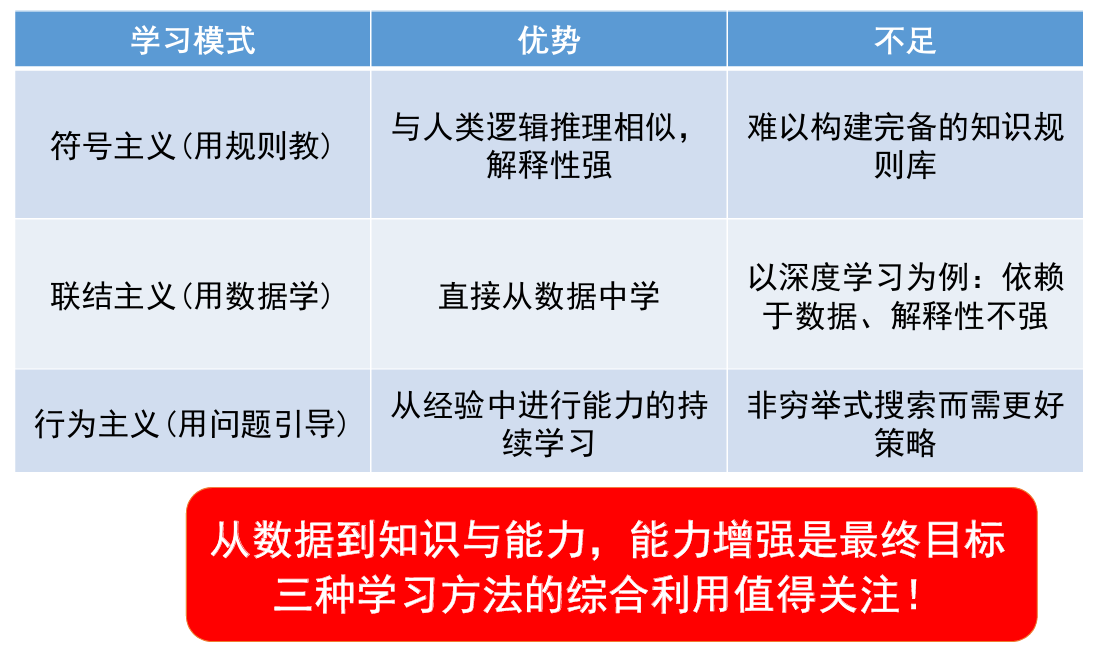
机器学习及有监督学习
机器学习基本概念
机器学习:就是从数据中学习知识,找到函数f(x)=y。
按问题分类可分为:
- 回归问题(如预测PM2.5),输出为数值
- 分类问题(如垃圾邮件过滤),给定选项,输出一个正确选项。
按数据标注情况可分为:
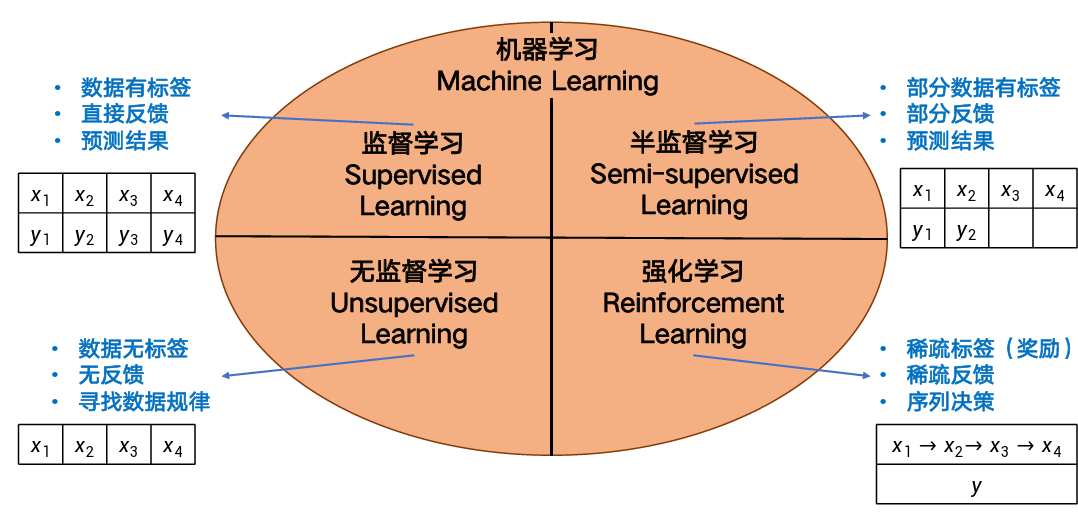
监督学习
监督学习的要素:
- 标识数据:标识了类别信息的数据
- 学习模型:定义映射模型类型
- 损失函数:对映射结果进行度量
- 优化方法:对映射模型进行学习
训练集一共有n个标注数据,第i个标注数据记为(xi,yi)。
-
训练映射函数(模型)f,使得f(xi)的预测结果尽量等于yi。
-
损失函数Loss就是用来计算xi真值yi与预测值f(xi)之间差值的函数。
-
典型的损失函数:

-
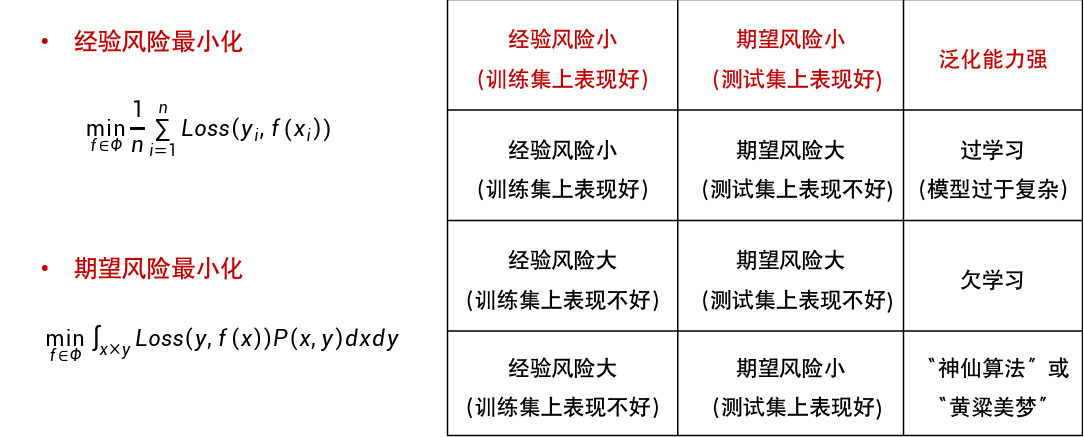
在训练过程中希望优化映射函数,使得在训练数据集上得到“损失”之和最小,即
-
如何评价一个模型的好坏?
-
经验风险:训练集中数据产生的损失。经验风险越小说明学习模型对训练数据拟合程度越好。
-
期望风险:当测试集中存在无穷多数据时产生的损失。期望风险越小,学习所得模型越好。
-
过学习与欠学习:
-
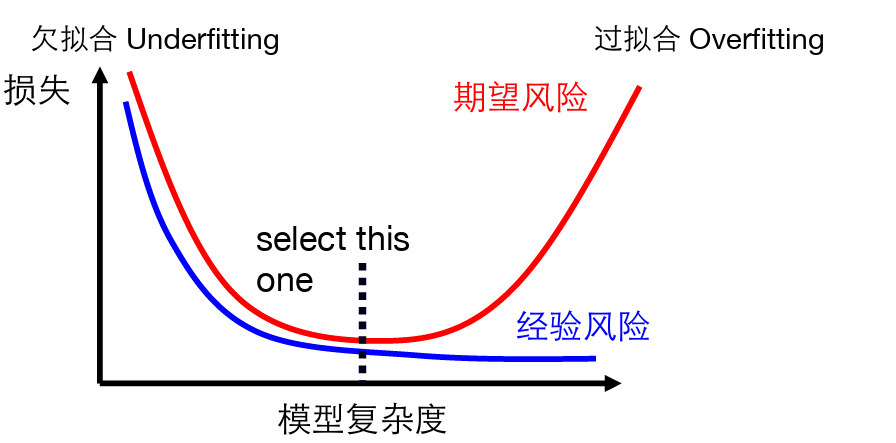
限制模型复杂度→避免过学习
-
-
结构风险最小化:在最小化经验风险与降低模型复杂度之间寻找平衡。
-
监督学习两种方法:判别模型与生成模型。
- 判别模型直接学习判别函数或条件概率分布作为预测的模型;关心在给定输入数据下,预测该数据的输出是什么。
- 生成模型从数据中学习联合概率分布P(X,Y),通过
线性回归
回归分析:分析不同变量之间存在的关系。
一旦确定了回归模型,就可以进行预测等分析工作。
- 训练数据:
- 学习模型:
- 损失函数:
- 优化方法:最小二乘法
- 对损失函数
- 对b求偏导,得到
- 再利用上式对w求偏导,得到
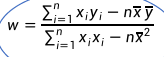
- 代入训练数据,解得w和b的值,获得一元线性回归模型。
- 对损失函数
多元线性回归:(影响y的有多个因素x,也就有多个w)
-
数据向量的维度D:影响y的因素个数。
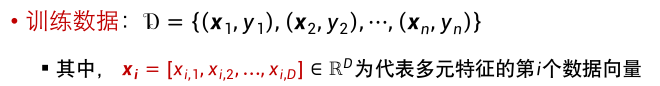
多元线性回归中,假设数据向量的维度为D,那么多元线性回归模型的参数量为D+1。
-
最后获得向量w(共D+1维度,w0即为b):

线性分类
线性回归的模型显然是不能直接拿来做线性分类的。
于是引入了对数几率回归(logistic regression)。
Logistic回归模型可如下所示:

这里的
函数图像:
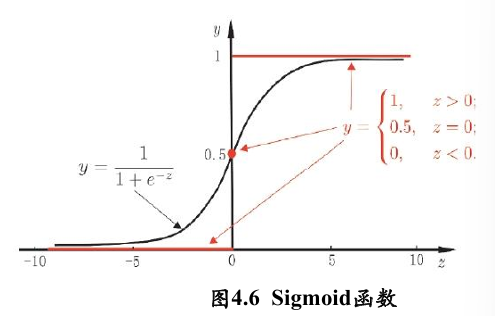
特点:
- sigmoid函数是单调递增的,其输出可以作为概率值;
- 数据特征加权累加:对输入z取值范围没有限制。
- 非线性变化:z=0附近变化大,但大于/小于一定数值后y无限趋近于1/0。
实际预测时,可以计算函数
由图可知:z=0的分界点正好是y=0.5的分界点。
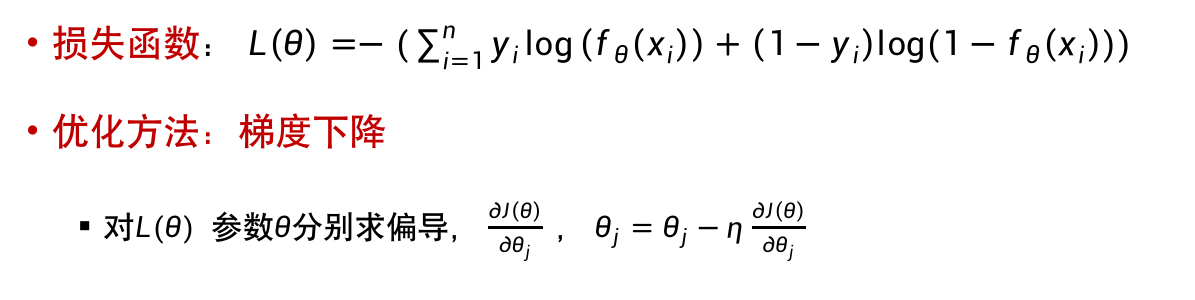
线性判别分析Fisher
基于监督学习的分类/降维方法,也称Fisher线性判别分析(LDA,FDA)。
对于一组具有标签信息的高维数据样本,利用其类别信息,将其线性投影到一个低维空间,在低维空间中同一类别样本尽可能靠近,不同类样本尽可能远离。
步骤:
- 计算数据样本集中每个类别样本的均值
- 计算类内散度矩阵Sw和类间散度矩阵Sb
- 求解
- 通过矩阵W将每个样本映射到低维空间,实现特征降维或分类器学习。
支持向量机SVM
线性可分:有一条直线能将两部分分割开
三维:有一个平面能将两部分分隔开。
更高维度同理。
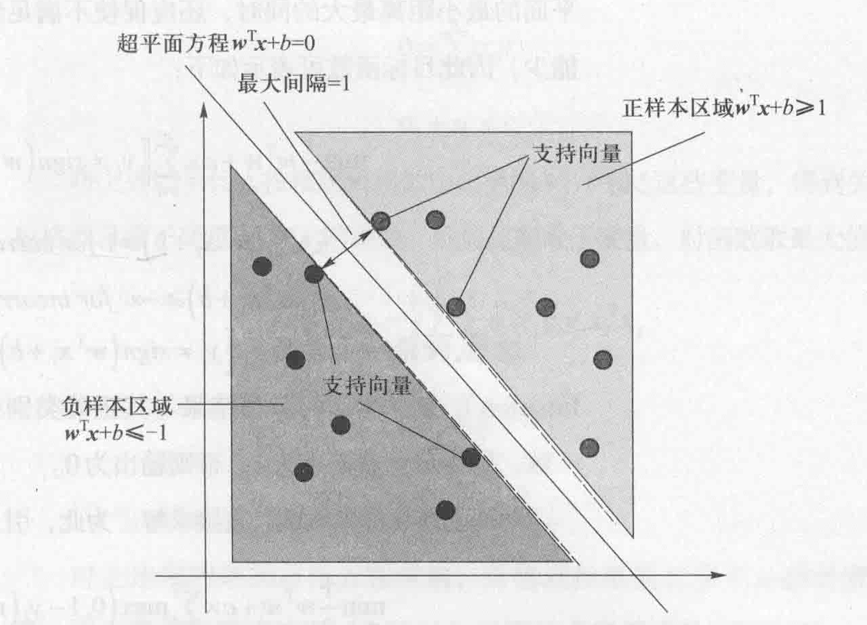
支持向量机的基本形式就是最大化分类间隔,即在满足约束的条件下找到参数w和b,使得γ最大。
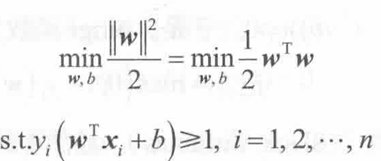
还可以通过拉格朗日对偶性变换到对偶向量的优化问题,引入拉格朗日乘子α:
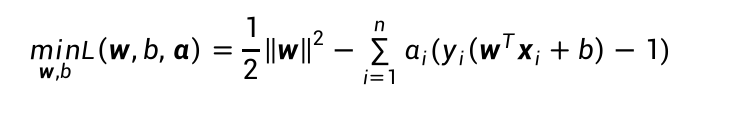
线性不可分的情况:
选择一个核函数,通过将数据映射在高维空间,来解决在原始空间中线性不可分的情况。
低维不可分,但一定存在一个高维特征空间使样本可分。
决策树
三种依据的公式要会背&会算。
通过树形结构来进行分类。
- 内部节点代表一个属性或特征
- 叶节点代表一种类别
- 分支代表一个判断预测输出
衡量样本集合“纯度”的指标:信息熵。信息熵越大,说明该集合的不确定性越大,纯度越低。选择属性划分样本前后信息熵的减少量被称为信息增益。
建立决策树的关键:寻找最优划分方式,使得每个结点的纯度越来越高。
-
信息(经验)熵:
-
条件熵:在a给定条件下,Y的条件概率分布的熵对a的数学期望
条件熵
-
信息增益:
(划分前的信息熵-划分后的条件熵)
两个条件a相比,谁带来的信息增益越大,越倾向于选择谁进行划分。
信息增益的缺陷:变量较多的属性更容易被选择。
为了避免这种情况,通常先找出信息增益较高的属性,再从中选择增益率最高的。
-
信息增益率:

-
基尼系数:反映了从数据集D中随机抽取两个样本,其类别标记不一致的概率。越小越好。
基尼值:
属性a的基尼指数:
决策树训练流程
-
从空决策树开始
-
选择下一个最佳属性进行划分,选择依据:
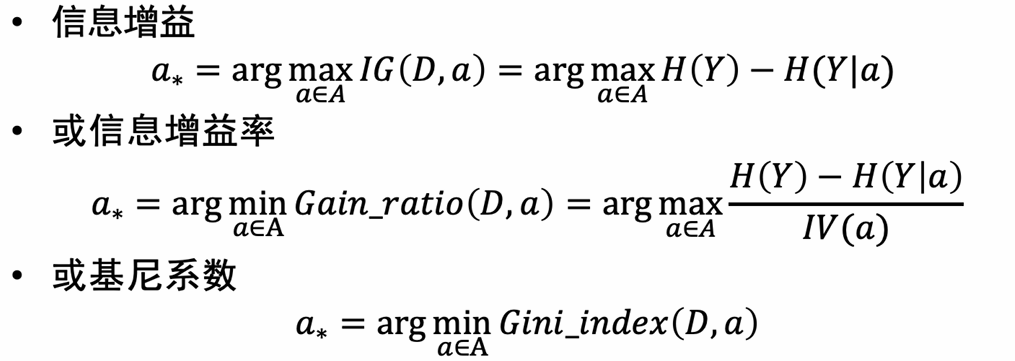
-
迭代
划分选择与剪枝
划分选择的各种准则虽然对决策树的尺寸有较大影响,但对泛化性能的影响很有限。
简直方法和程度对决策树的泛化性能的影响更为显著。
剪枝是决策树应对“过拟合”的主要手段
剪枝的基本策略:
- 预剪枝:提前终止某些分支的生长
- 后剪枝:生成一棵完全树,再回头剪枝。
剪枝方法:剪掉某节点为根节点的子树;将该节点设置为叶节点。
集成学习Ada Boost
集成学习通过构建并结合多个学习器来提升性能。
集成的个体应该:好而不同。
Ada Boost迭代算法步骤:
- 初始化训练样本的权值分布,每个样本具有相同权重。(权重和为1)
- 训练若分类器,如果样本分类正确,则在下一个训练样本集中降低它(这个样本)的权值;反之提高。用更新过的样本集去训练下一个分类器。
- 将所有的弱分类器组合成强分类器。各个弱分离器的训练过程结束后,加大分类误差率小的弱分类器的权重,降低分类误差率大的弱分类器的权重。
某个分类器的错误率:
弱分类器权重:
迭代后样本权重:
其中
强分类器
深度学习
深度学习与传统机器学习的区别:
-
深度学习适合处理大数据,机器学习算法更适用于小数据。
-
机器学习需要手动进行特征构造,深度学习能通过多层神经网络自动学习特征
-
深度学习需要大量计算资源,比如GPU。
-
深度学习通常利用“端到端”的方式构造模型,机器学习通常将问题分为几个步骤,每个步骤逐一解决,然后将结果组合。
线性回归与梯度下降
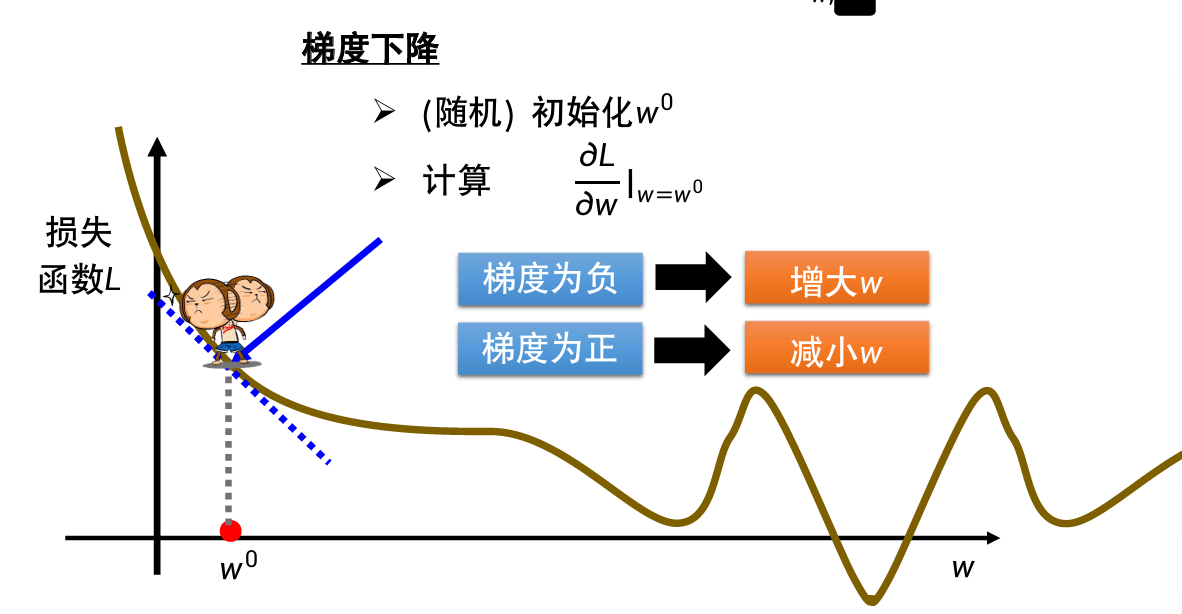
w的增大/缩小程度:
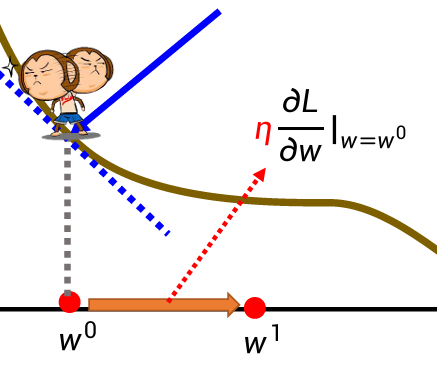
不断调整,当到达局部最低点时会暂停,不一定能找到全局最低点。
优化:求
深度学习的训练过程:
- 定义带有未知参数的函数
- 从训练数据中定义损失函数
- 优化
梯度下降公式:
梯度反方向是函数值下降最快方向。
其中
前馈神经网络FC
线性模型的扩展:
分段线性函数。可以用分段线性模型拟合连续曲线。
对于Sigmoid函数
更改
在这里sigmode叫做激活函数,sigmode也可以换成其他函数,比如ReLU。

然后将这3段(或更多段)组成一个新的函数
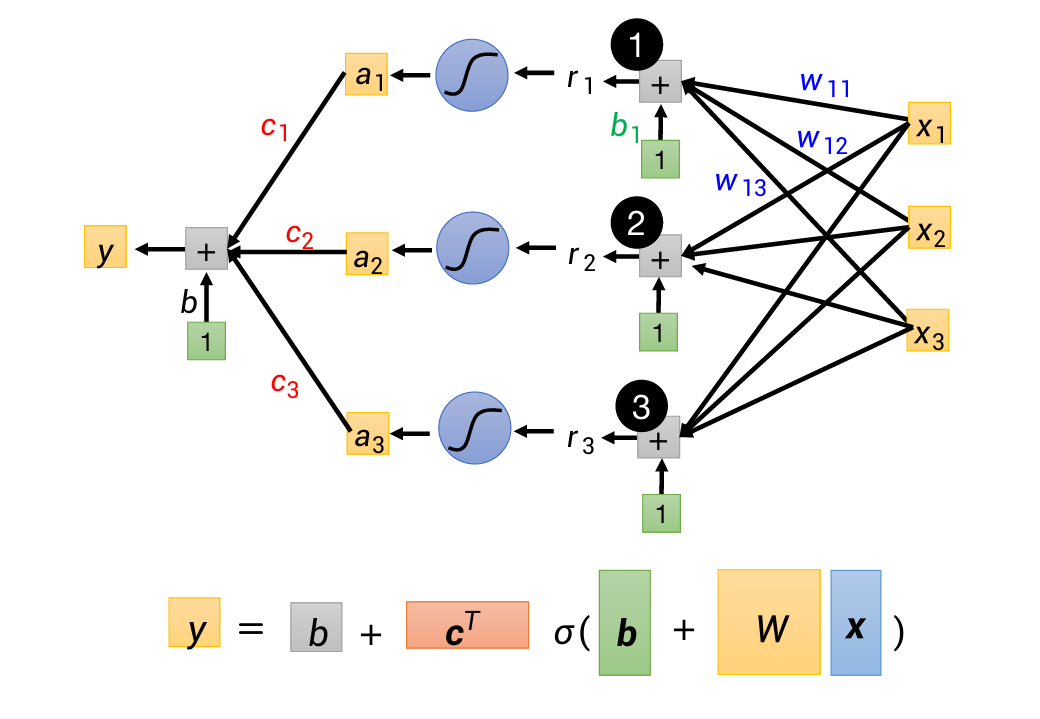
这是一个隐藏层(hidden layer)。可以添加更多层隐藏层。
这就是新的model了。
位置函数包括:b,c,b,W(加粗为向量)
优化:梯度下降方法,依然是求L对所有参数θ的偏导,迭代更新所有参数。


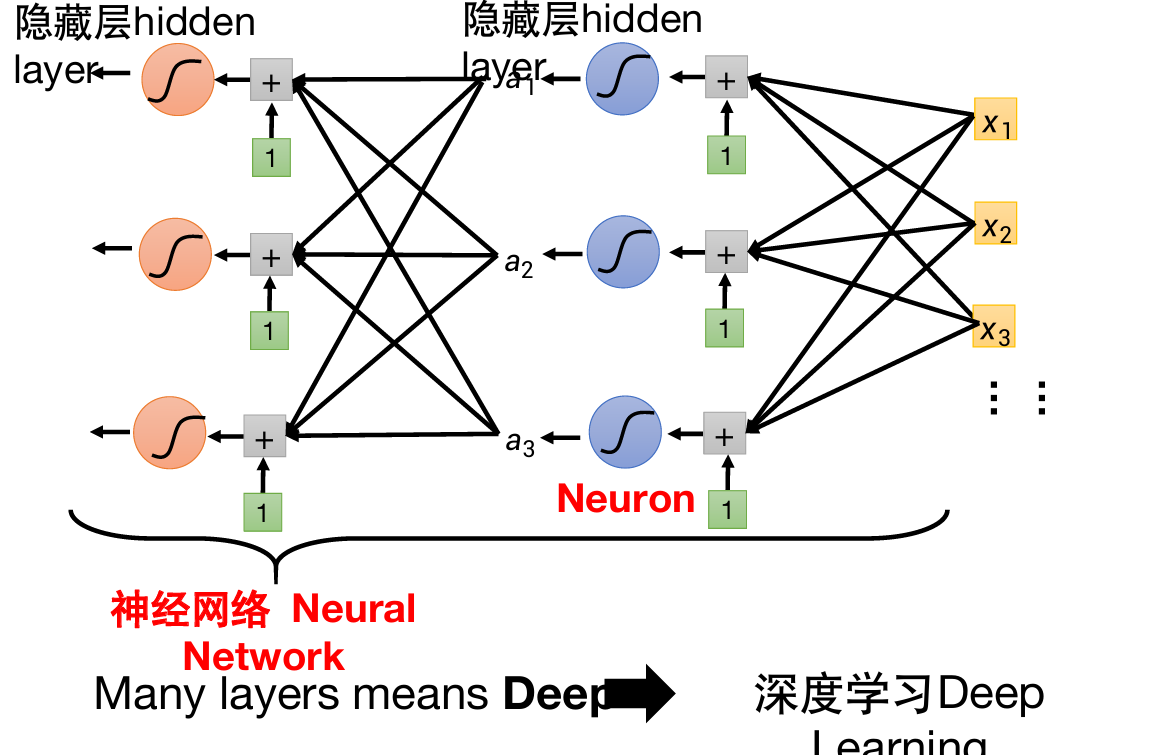
- 前馈神经网络由输入层、输出层和至少一层的隐藏层组成。网络中各个隐藏层中神经元可接受相邻前序隐藏层中所有神经元传递而来的信息,经过加工处理由将信息输出给后续相邻隐藏层中所有神经元。
- 各个神经元接受前一级的输入,并输出到下一层,模型中没有反馈
- 层与层之间通过全连接进行链接:两个相邻层之间的神经元完全成对连接,但层内的神经元不相互连接。
- 也被称为全连接网络,或多层感知机。
卷积神经网络CNN
例:用于图像分类。
对于计算机来说,一张图片是一个三维的tensor,包括图片的宽、高、3个通道channel(rgb)。
宽高100*100,channels有三个,分类特征1000类,则一层全连接网络需要参数3*107个。太多了!
实际上识别图像并不需要全覆盖,只要找到某几个特定的patten(模式)即可实现识别。
名词:
- 感受野:3*3*3,彼此之间可以重叠
- 卷积核:高与宽,3*3。
简化1
覆盖3个chennels,卷积核大小一般为3*3;
每个感受野覆盖一组神经元;
每个感受野之间有一定重叠,平移的量为stride(自己设置)。
超出整个图像范围则对超出部分(padding)补0。
感受野覆盖全图。
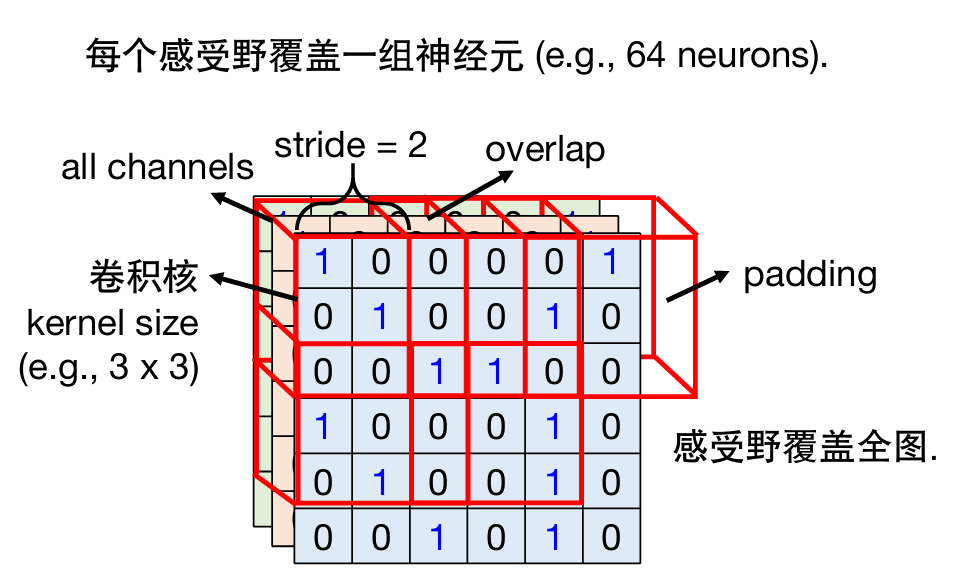
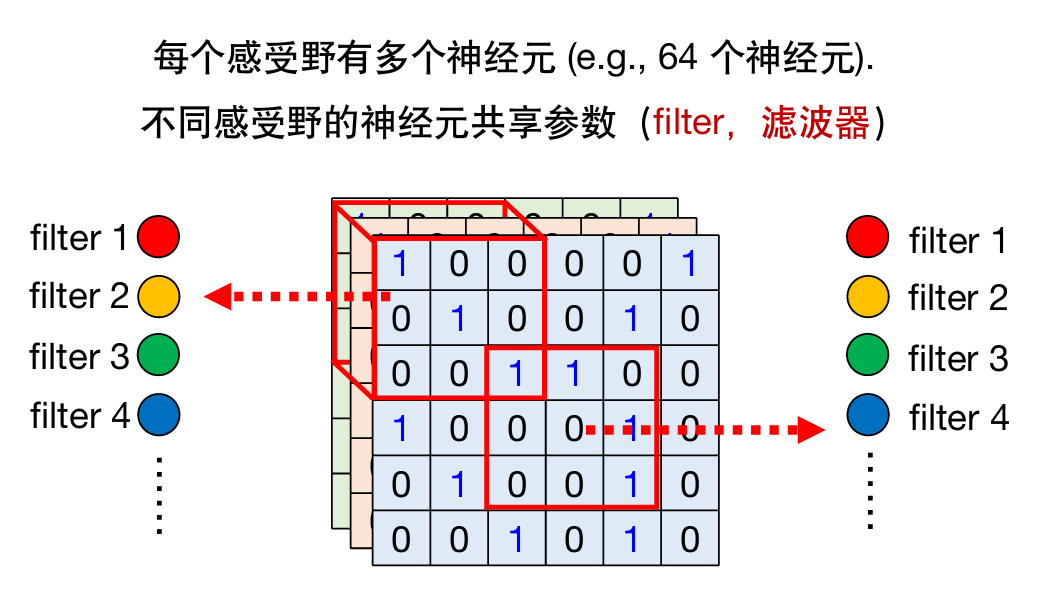
简化2
同一感受野的不同神经元不共享参数;
不同感受野的神经元共享参数。
下图中颜色一样代表参数共享。
卷积层的优势
- 通常pattern会远小于整图大小
- 同样的pattern会出现在图上不同区域。
卷积层的另一种解释
上一层的filter个数→下一层的channels个数→下一层filter高度
池化
对图片做降采样,不会对结果有影响。
池化有很多版本,这里介绍最大池化:
获得一个特征图后将其分成若干组,每组中取最大的留下:
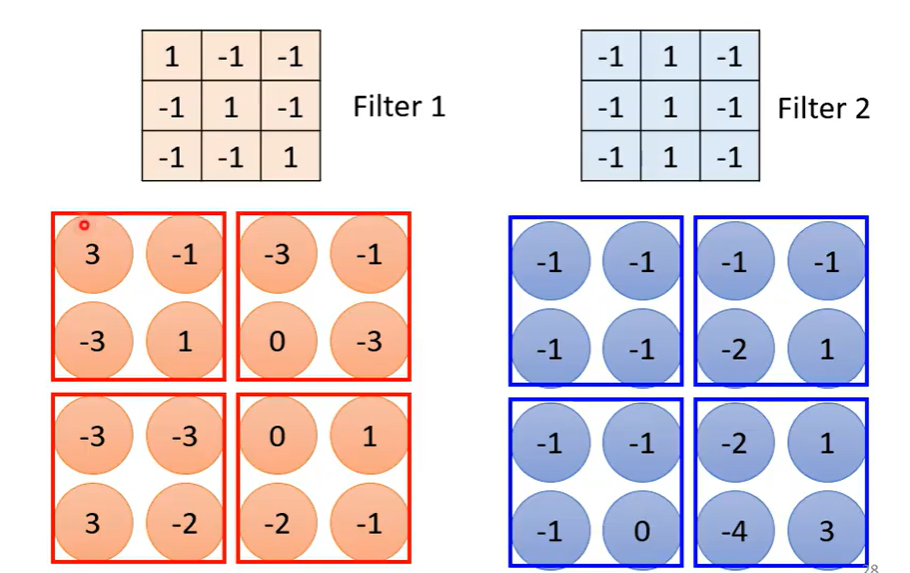
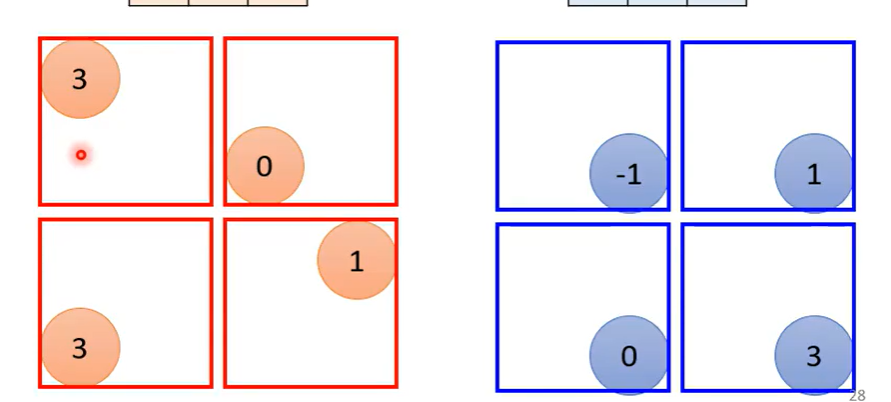
在很多次卷积和池化交替后,最后需要一次Flatten:把所有向量拉直,通过激活函数获得最终的分类结果。
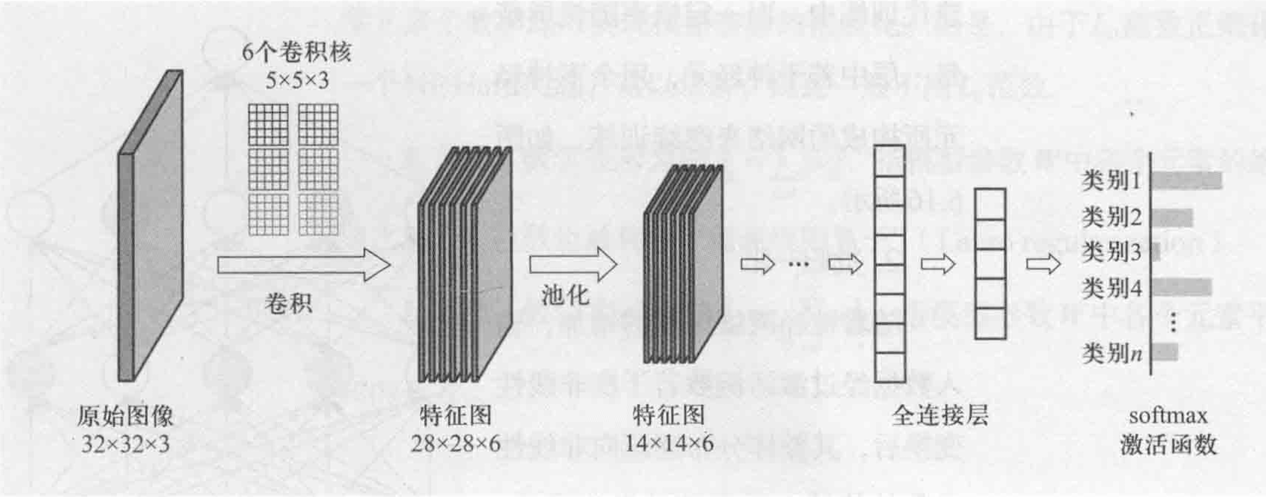
CNN的问题和不足
CNN中的卷积操作不满足尺度和旋转不变性,需要数据增广。
序列数据模型
之前讨论的都是向量输入。
当输入非常复杂、为一个向量集时:
输出形式有一对一输出、多对一输出、多对多输出;这里介绍一对一输出(输入与输出数目一样多)。
如果使用全连接(前馈神经网络,FC),会导致无法注意到如前后文等信息。
自注意力机制self-attention
所有pattern都是在考虑整个sequence的信息后才得出的。
可以交替使用自注意力和全连接。
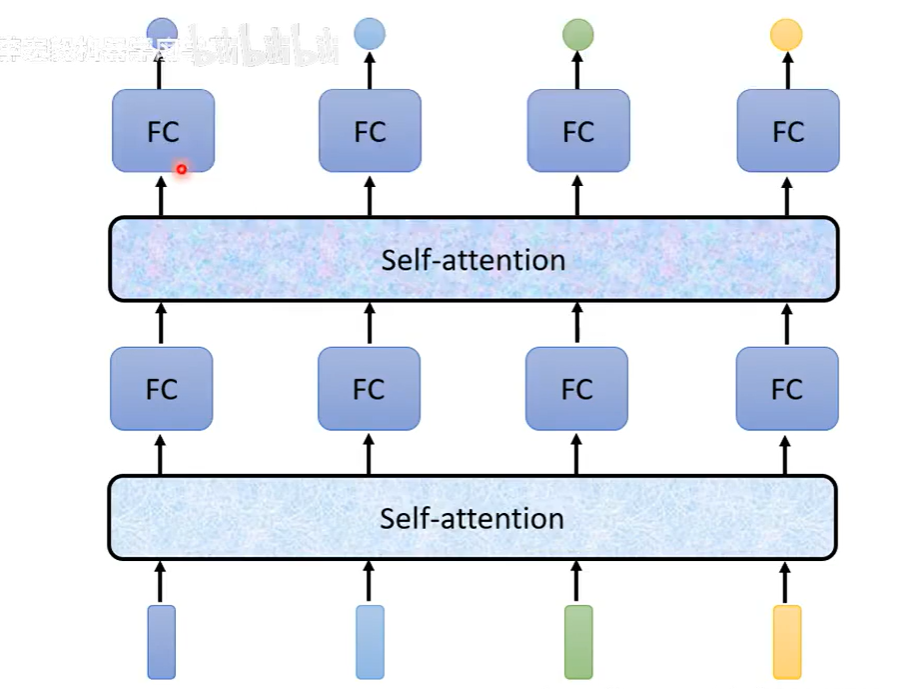
自注意力机制的运作原理
每一个b都是在考虑所有a后才产生的。
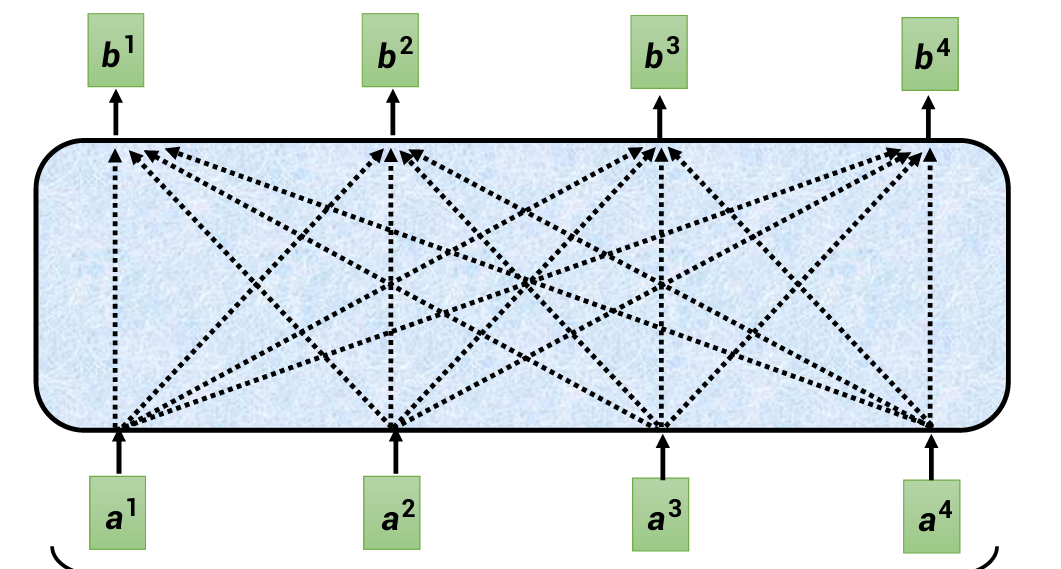
对于单独一个b(如b1):需要考虑a2、a3、a4分别与a1的关联度α。
计算α的方式:
第一种:
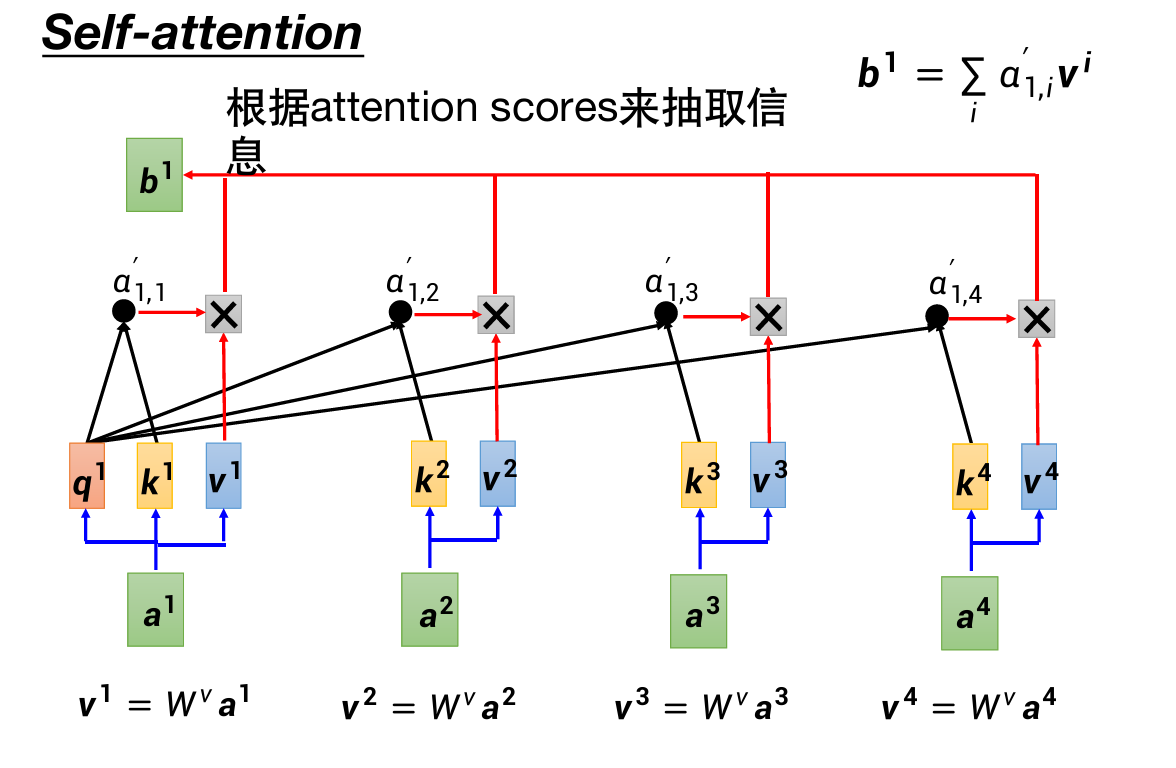
第二种理解视角:
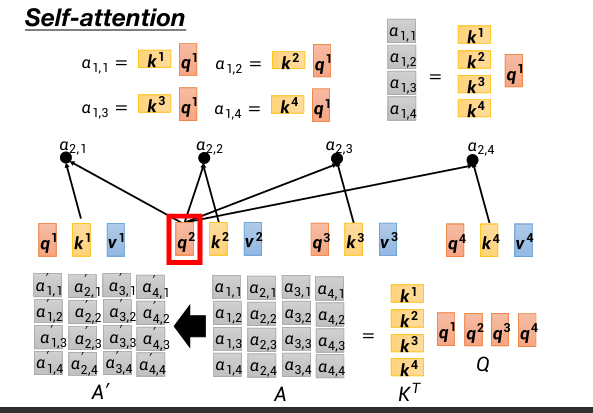
然后计算出b1、b2、b3、b4:

整个过程:(矩阵形式)
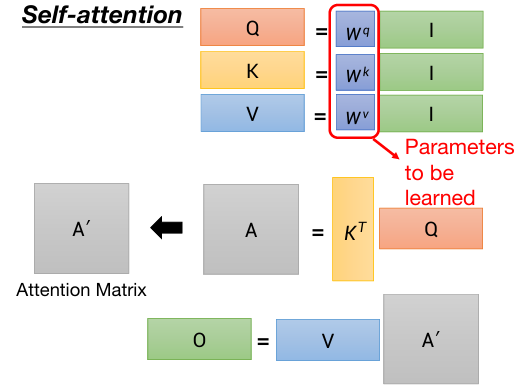
其中,只有Wq Wk Wv是需要学习得来的。
这一部分主要考矩阵计算。
位置编码
self-attention中缺失了位置信息(例如单词顺序)
可以给每个位置赋予一个唯一的位置编码向量,它可以是手工设计的,也可以是从数据中学习的。
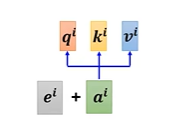
自注意力机制 vs CNN
CNN是简化版的self–attention。
self-attention弹性较大,需要的训练资料比较多;CNN则相反。
自注意力机制 vs RNN
RNN:循环神经网络
RNN无法平行处理所有数据,但self–attention可以,所以后者在运算上更有效率。
模型训练策略
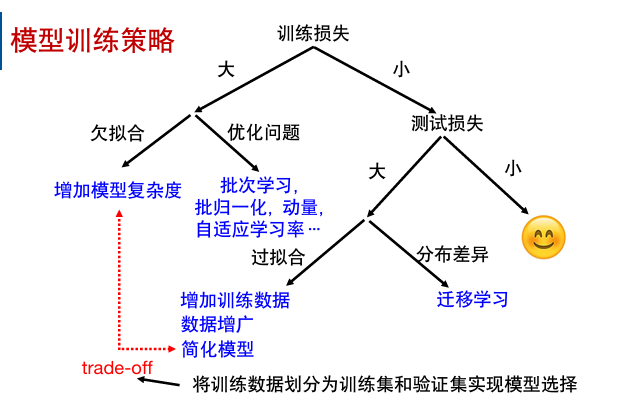
深度学习应用
seq2seq
输入一个sequence,输出一个sequence。
不知道输出的长度,需要机器自己来决定。例如语音识别、翻译、语音传译。
Transformer
self-attention的应用。
Encoder
给一排向量,输出一排向量。
可以用CNN、RNN、self–attention等方式。
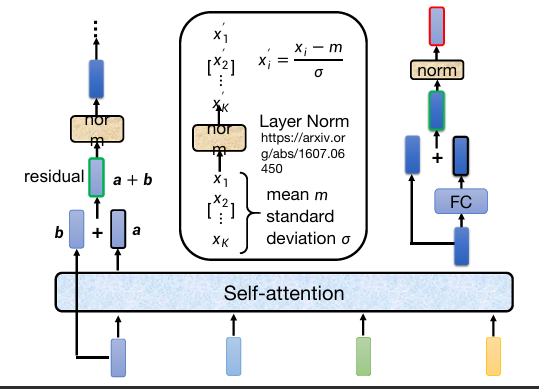
Decoder
会把自己前一时刻的输出当成现在时刻的输入。
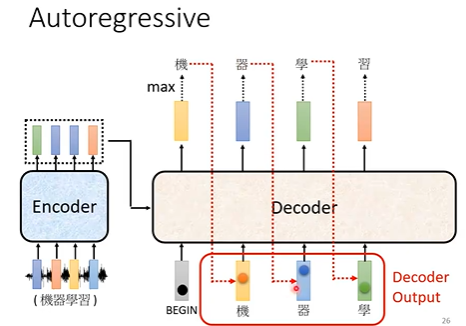
NAT的好处:可以控制decoder的长度,可以并行
AT:NAT 通常效果比AT差
BERT
self-attention的应用,“填空题”。
属于自监督学习。
BERT的功能和Transformer的Encoder功能一样。
掩码输入:随机覆盖一些tokens。可以使用特殊字符,或随机替换成其他字符。
BERT的学习目标:成功预测出被掩盖的文字(属于的类别)。
下一句预测:输入时在两个句子中添加分隔符号;输出Yes/No,判断两个句子是否相接。
但是BERT可以被用在更多的下游任务上,不限于以上两种训练任务。
在用于下游任务时,需要少量的标注参数。
GPT
没考,鸽了
无监督学习
K均值聚类算法
目标:将n个数据聚类到k个集合。
两个m维数据之间的欧氏距离为:
步骤:
-
初始化聚类质心
初始化k个聚类的质心,质心ci可以从n个数据中采样获得。每个聚类的集合记为Gj。
-
将每个待聚类数据放入一个聚类集合中
计算待聚类数据xi与质心cj之间的欧式距离;将xi放入与之距离最近的聚类集合中。
-
更新聚类质心
根据每个聚类集合中包含的数据,更新该聚类的质心值。
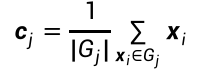
-
循环迭代,直到:达到迭代次数上限,或前后两次迭代中聚类质心基本不变。
不足:
- 需要事先确定聚类数目
- 需要初始化聚类质心,且对结果有较大影响
- 算法迭代执行,时间开销大
- 欧式距离假设每个维度之间的重要性是一样的。
主成分分析PCA
网课P88,unsupervise
目标:实现特征降维,去除原始数据之间的冗余性。即有一个向量x,要将它转化为维度更低的向量z。z=Wx,要找出W。
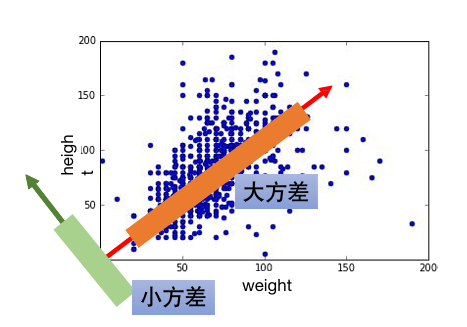
如上图这种,需要找一个方向(W),将二维降成一维。
为了保存数据所蕴含的信息,降维投影时应该尽可能将数据向方差更大的方向投影。
即希望映射后的数据z1的方差尽可能大。
推导过程:

其中,Var(z)表示z的方差;
Cov(x)表示协方差,用S表示。
问题转化为:找一个w1使得蓝框中的式子最大。
当然w1不能直接取无穷大……所以添加了限制条件:
(跳过计算过程,直接上结论……)
w1是协方差矩阵S的一个特征向量,对应于最大特征值λ1;
w2是协方差矩阵S的一个特征向量,对应于第二大特征值λ2
综上,主成分分析的步骤:
- 数据预处理
- 计算协方差矩阵
- 求得协方差矩阵
- 取前
- 给定一个样本xi,可以将其从d维空间下降到
- 将所有降维后数据用Y表示,有
PCA的缺点:
-
因为PCA是无监督的,可能会把两组数据混在一起处理。
-
PCA是线性的,无法处理曲面数据。
PCA与Fisher的异同
其他常用降维方法:
- 非负矩阵分解NMF
- 多维尺度法MDS
- 流形学习:局部线性嵌入LLE
- PCA、NMF、MDS都属于线性降维方法,LLE则是非线性降维方法。
生成式人工智能
自编码器
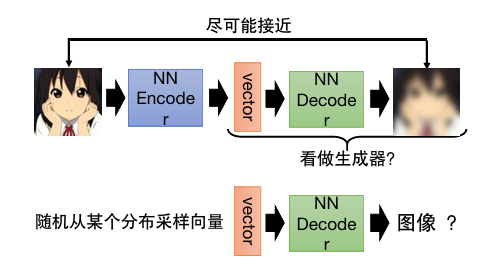
随机从某个分布采样向量作为输入,会导致输出可能根本不是图像。
因为实际上图像的类别是有限的。
去噪自编码器
将原来输入给自编码器encoder的图像加入杂讯后再输入,要求去噪并输出原来的图像。
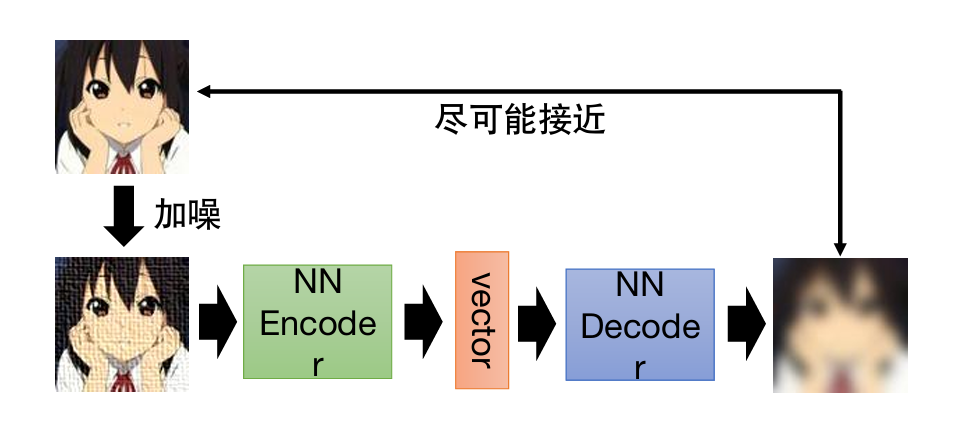
思想和BERT很相似。
从自编码器到生成模型
网课P55。
之前所学到的network都是一个函数,输入x→得到y。
现在,我们要把network当做一个生成器来使用。
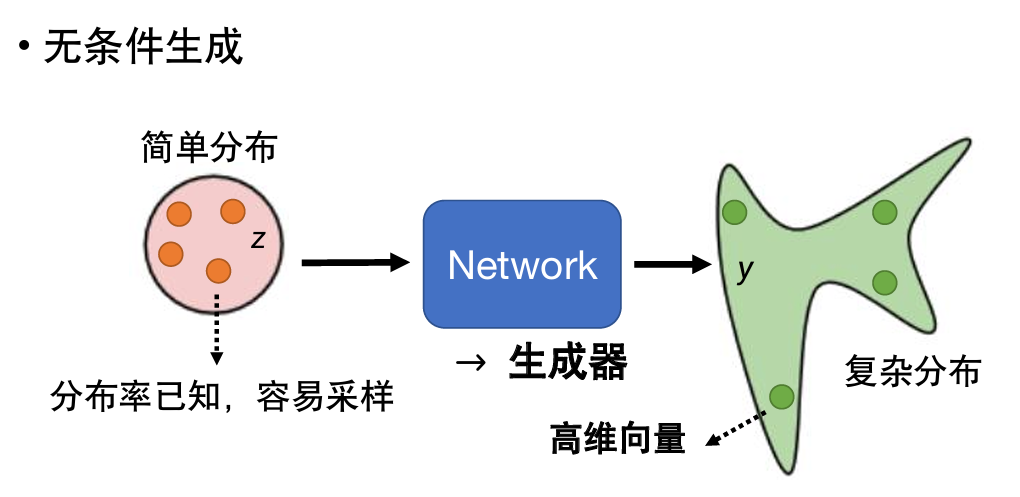
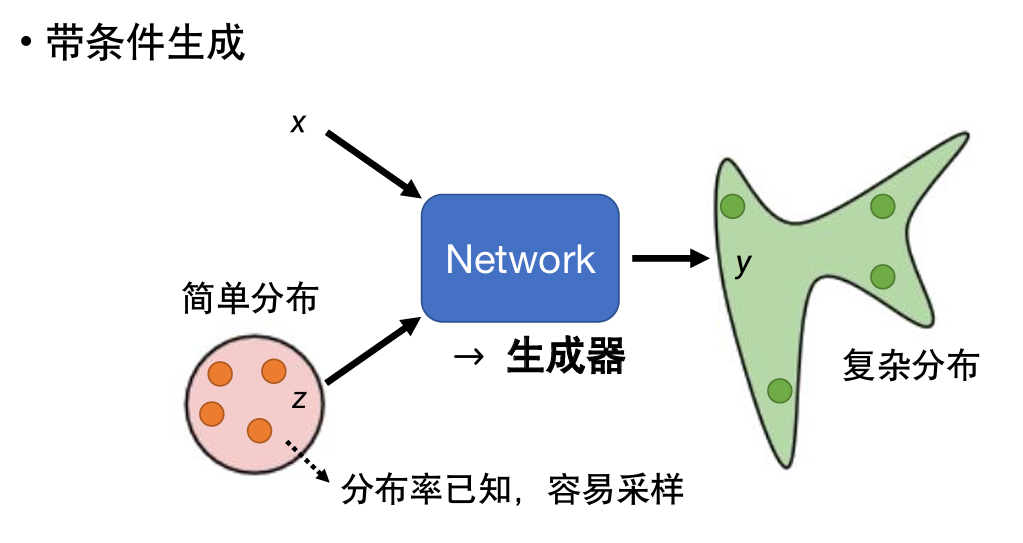
这种情况,可以把x和z两个向量连接、相加……等等操作后输入。
z的特别之处在于它是不固定的,每次使用network时z都会从简单分布中被随机采样出来。
为什么要训练生成器?
小精灵视频生成的问题。应该让机器的输出不是单一的,而是有几率的。
当我们需要一些“创造力”——需要很多种不同的输出时,就需要使用生成器。
例如绘图、对话,等等。
按李老师讲课顺序这里应该紧接是生成对抗网络GAN但你航要改我也没办法
变分自编码器VAE
或B站P62,Unsupervise
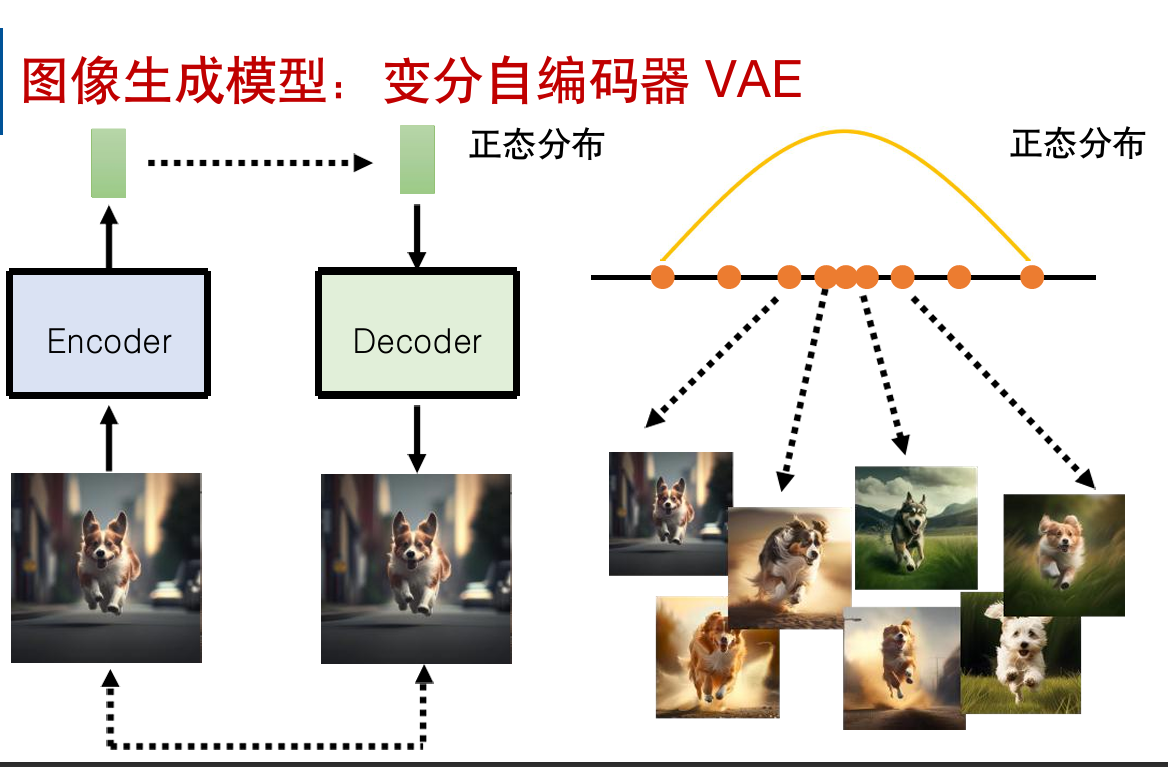
向Encoder输入一张图片,输出一个向量;
把这个向量输入给Decoder,输出一张图片。
目标是让两张图片尽可能相似。
原理:
VAE和自编码器一样有一个Encoder,一个Decoder。
不同的是,VAE的Encoder会输出两组向量,另外需要采样一组来自正态分布的向量。
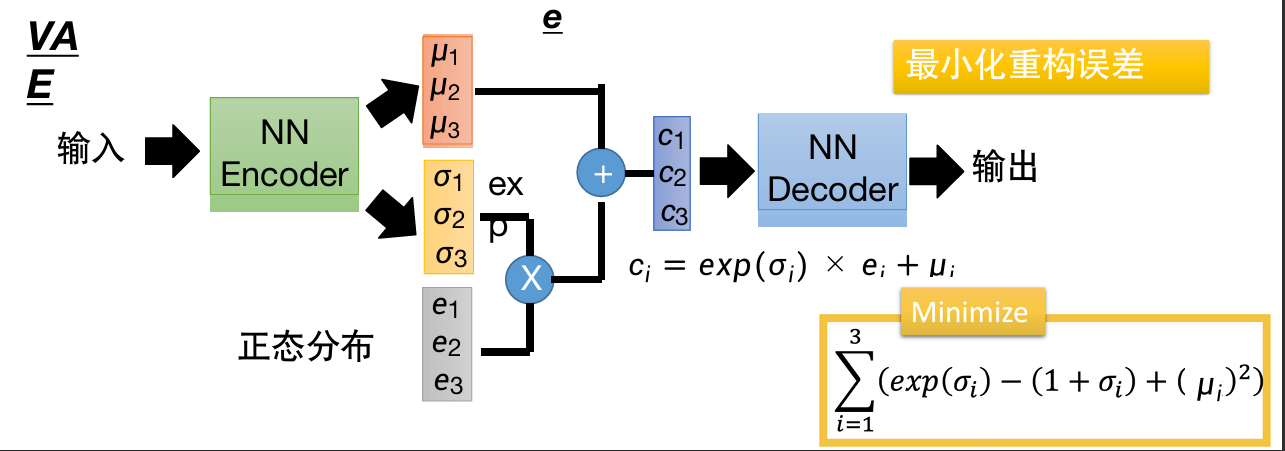
为什么需要VAE?直观的解释:
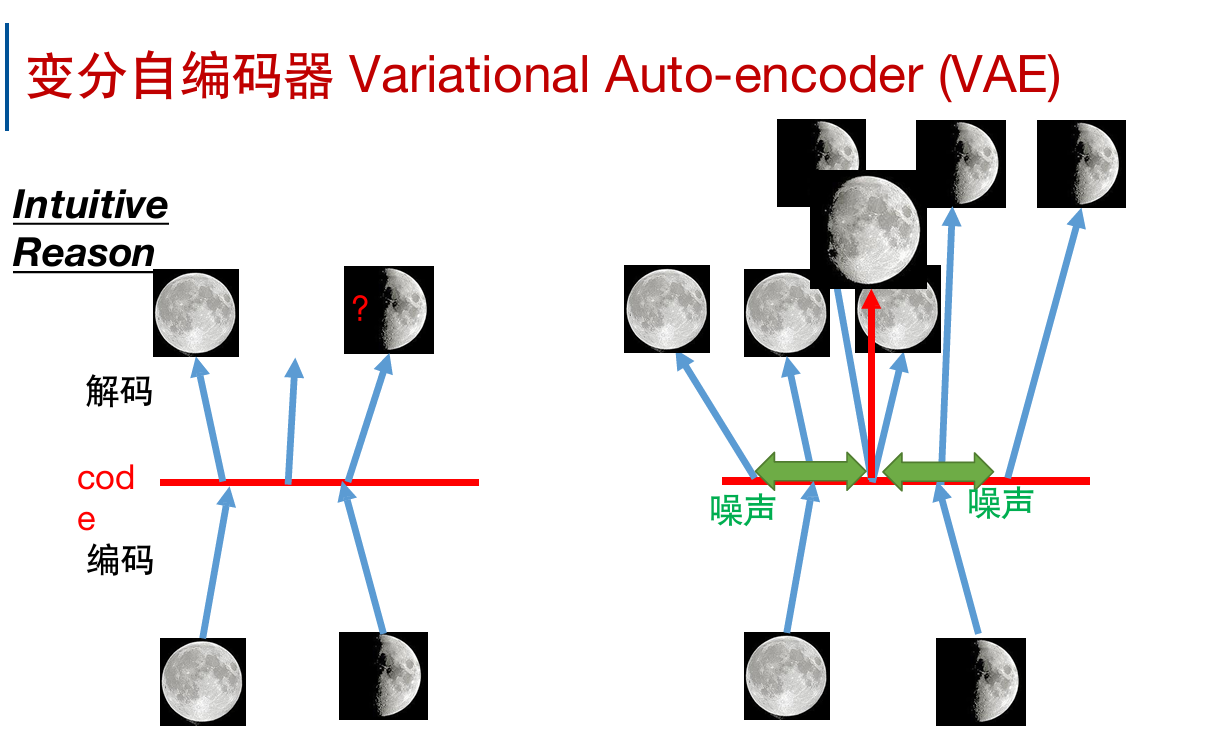
左边是自编码器,在满月和弦月中间生成不出来;
右边是VAE,添加了噪声之后,中间有一定重叠的部分;为了与两边都尽可能相近,中间就有可能生成介于满月和弦月之间的图。
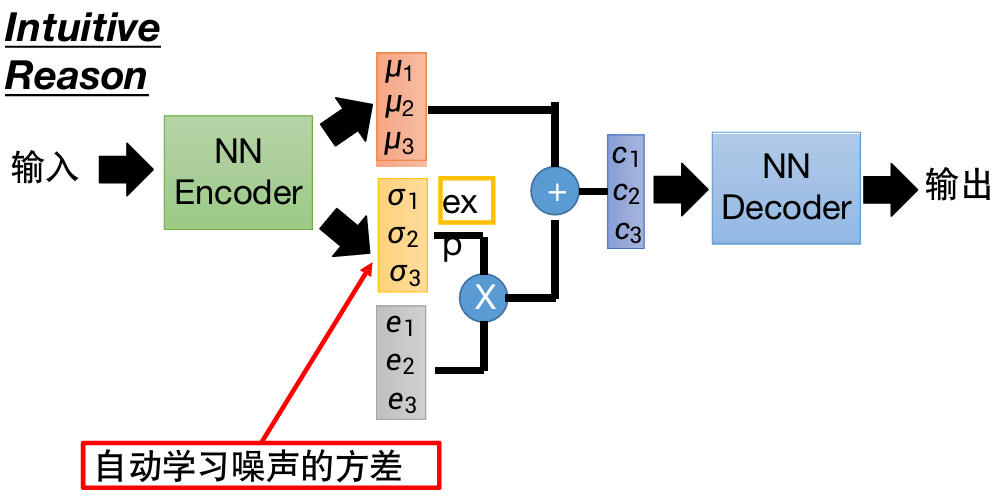
噪声的方差是自动学习的。
但是如果仅使用重构进行训练的话,自动学习来的方差会被学习为0。
所以需要对它添加限制(黄框式子)。

图中蓝色线、红色线分别为式子中的第一、第二项;式子中第三项是进行L2标准化。
绿色线则是两项相减。
最低点在σ=0的地方,所以我们希望σ接近0,即方差接近1。
正式的解释方法:

我们的目标是生成图片;每张图片可以视作高维空间中的一个点。
所以目标是实现对这个高维函数的概率分布估计,这样就可以从几率高的地方找到长得像pokemo的图(我们需要的图)。
可以使用高斯混合模型来实现概率分布估计。
高斯混合模型:由很多高斯分布叠加来的模型。
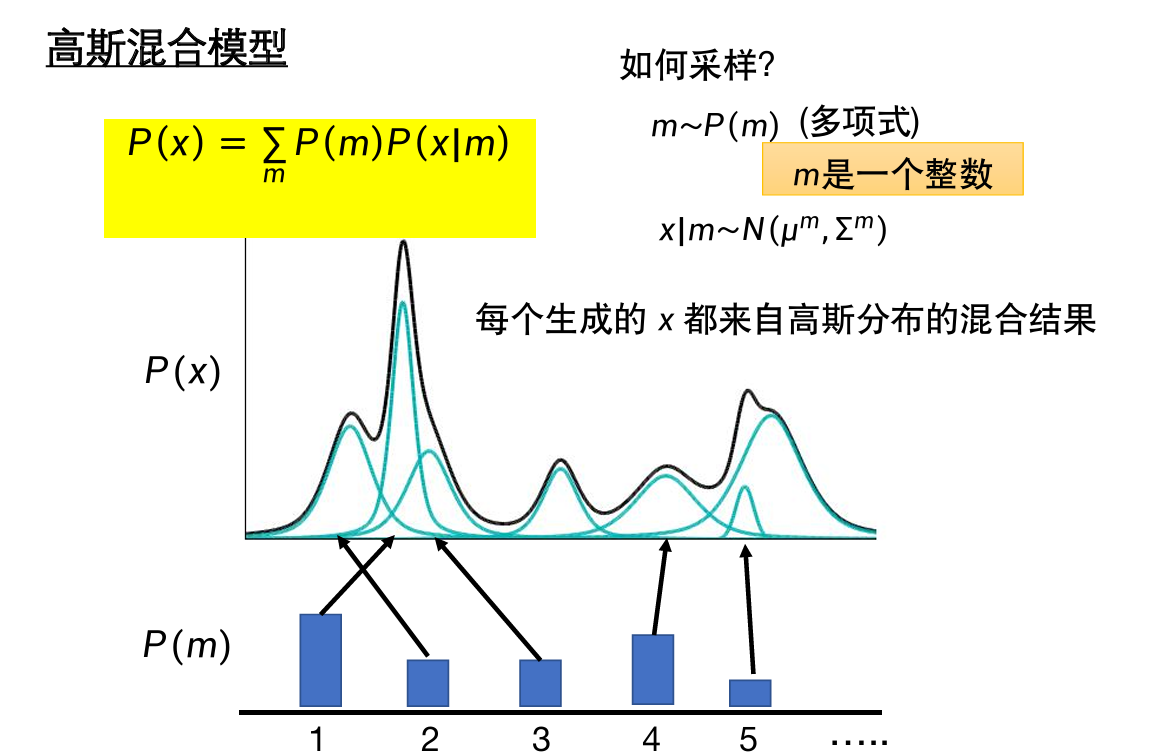
采样过程:
- 决定从哪个高斯函数中采样(决定m)
- 根据这个高斯函数获得x。(
- 此时,
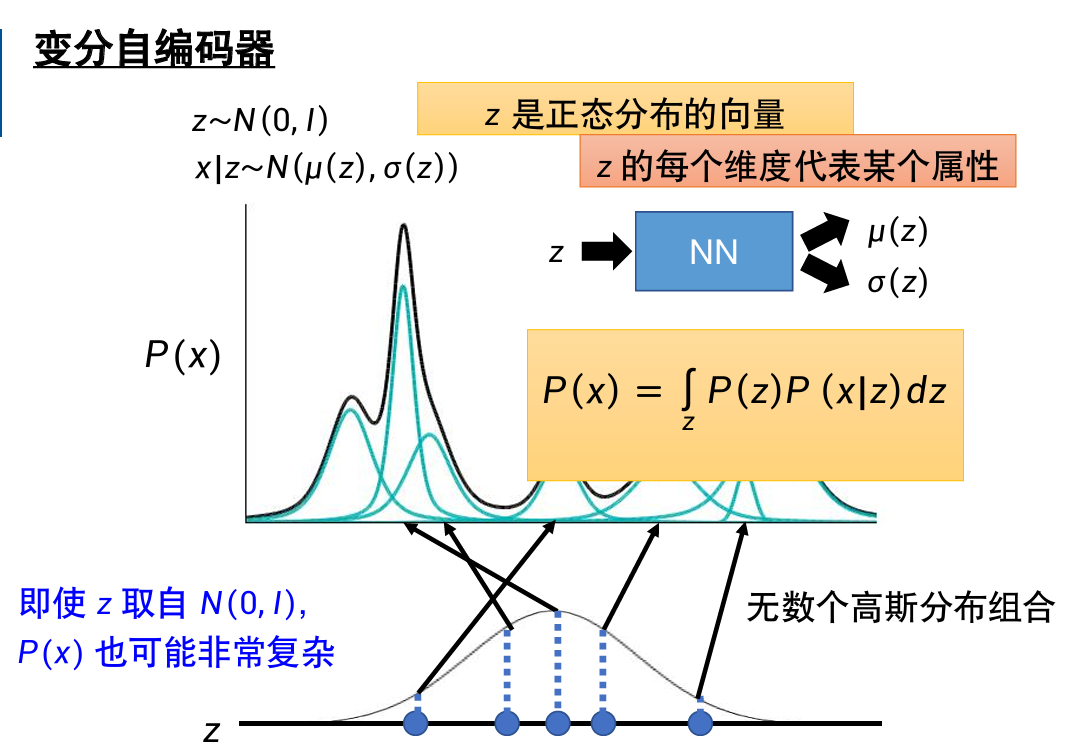
现在的目标:
取一组
x是我们看到的图片。
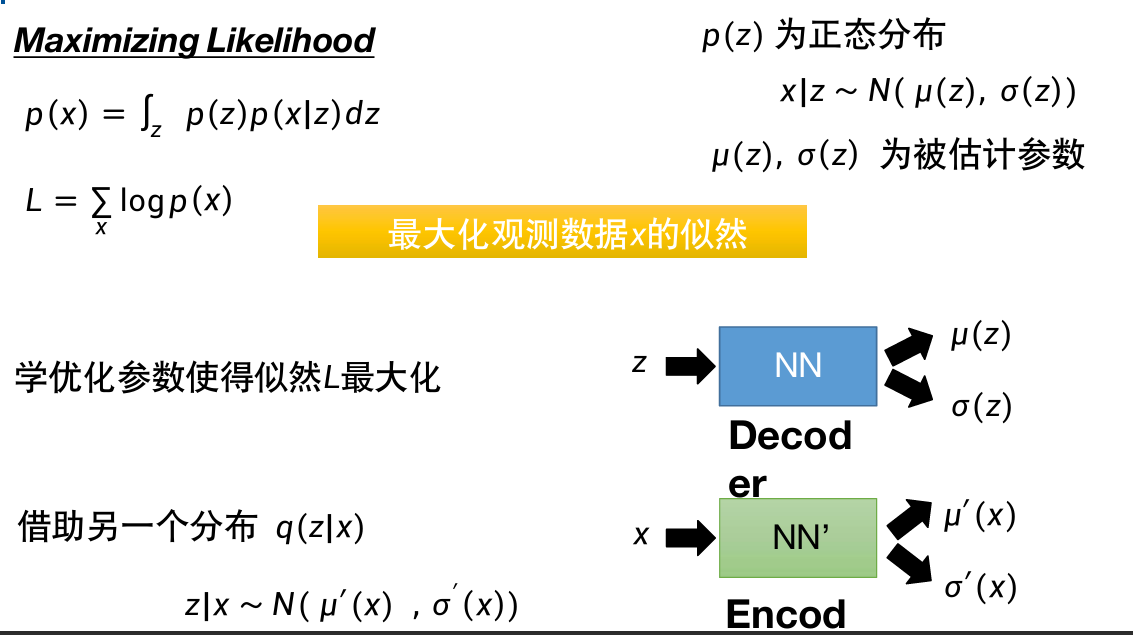
这里需要引入另一个分布
对

划线部分可以理解为两项之间的距离,一定是大于0的。
大于号右侧就是左侧式子的第一项,因为左侧式子第二项(划线部分)大于0,所以大于号成立。右侧记为下界Lb。
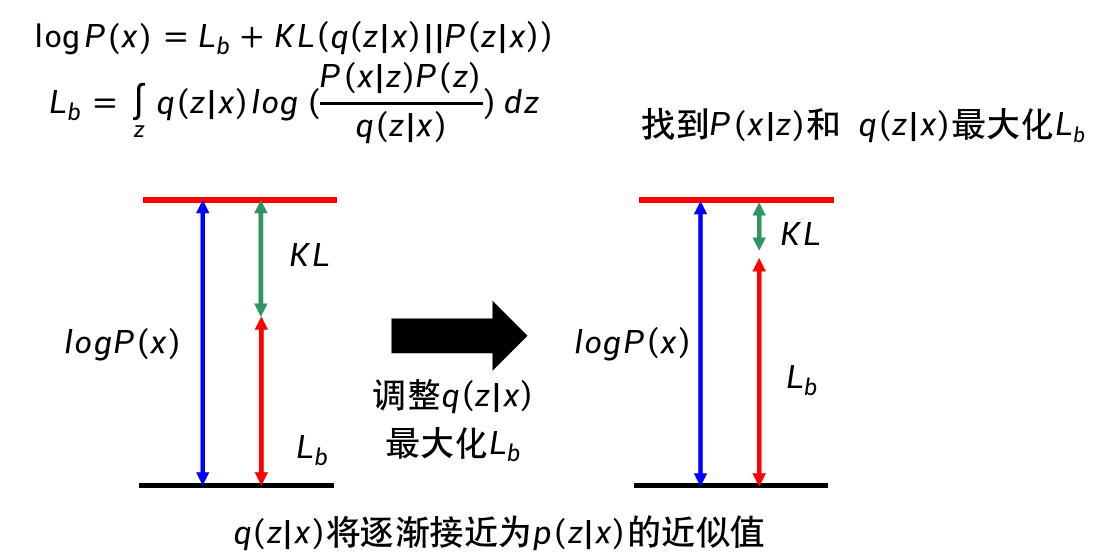
引入
的目的在于:避免Lb上升,但 不一定上升的情况。
与 无关,由图中可以看出,调整 使 变大时,会让 变小。
调整

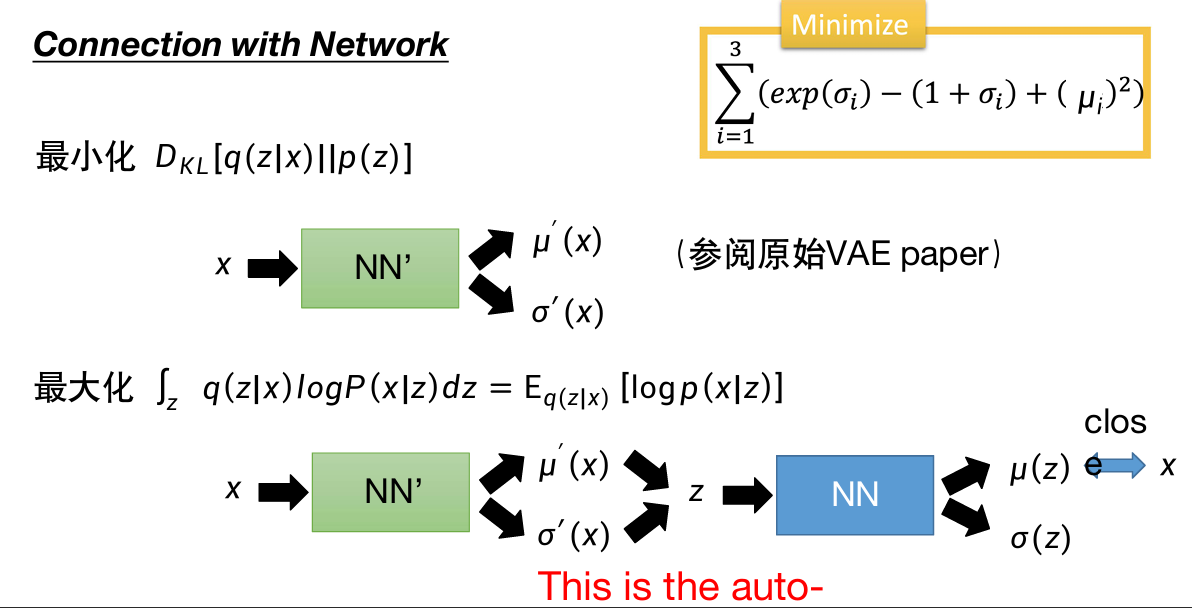
最小化
条件变分自编码器
可以根据某一个数字图像的特征生成很多同类的数字图像。
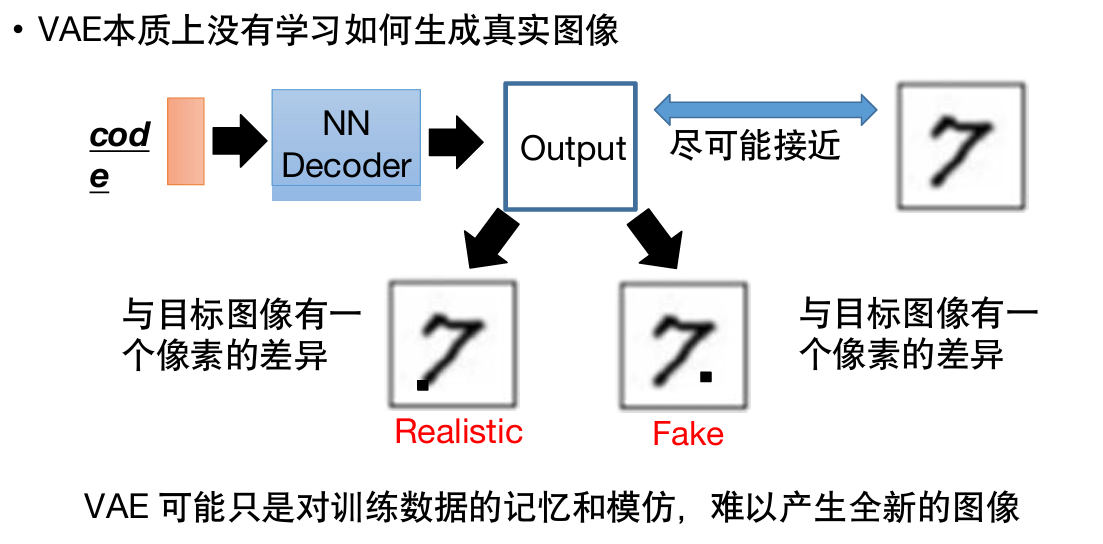
VAE的问题
本质上没有学习如何生成真实图像,只是在对训练数据进行记忆和模仿,学习怎么和数据集中的图片尽可能相似,难以产生全新的图像。
扩散模型Diffusion Models
网课P168。
扩散模型基本原理
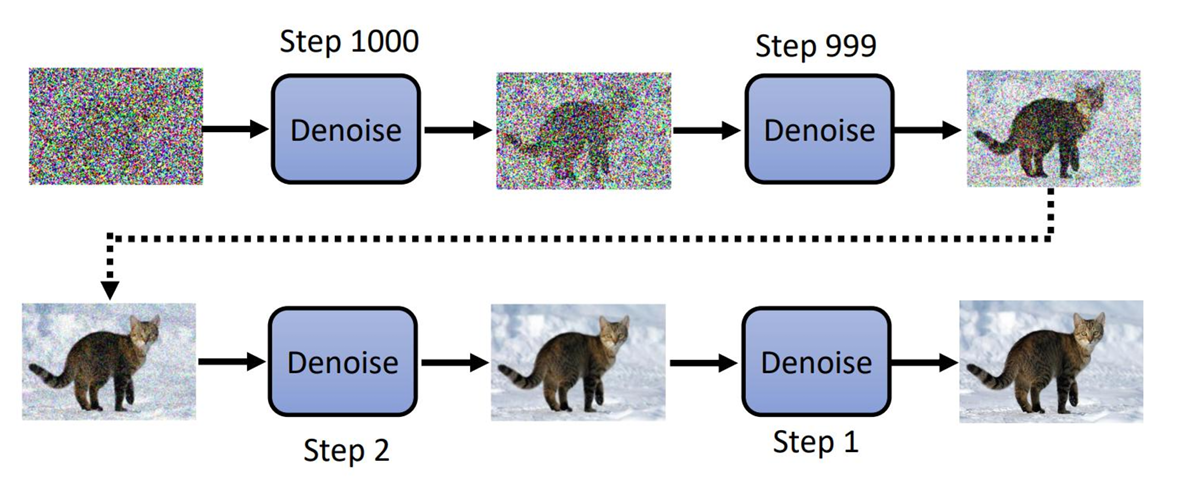
运作:首先给一张全是杂讯的图片(大小与期望的最终图片相同),然后不断做降噪。
“在我开始工作之前,雕塑已经在大理石块内完成。雕塑已经在那里,我只需要凿掉多余的材料”
图片已经存在于杂讯里,我们只是把杂讯去掉。
这里的Denoise模型都是同一个;但它除了需要输入图像外,还需要一个数字输入,表示现在杂讯的严重程度。
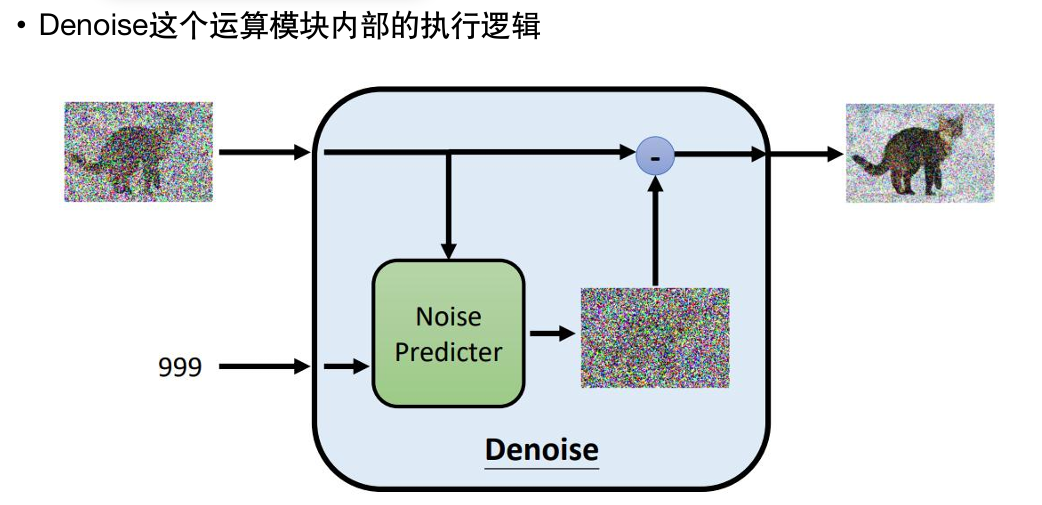
首先会根据目前杂讯的严重程度,生成一张杂讯图片;
再在原来图片的基础上减去生成的这张杂讯图片,实现“降噪”。
这个生成杂讯图片的过程所需要的资料是人类制造的:对原始图片不断加噪。
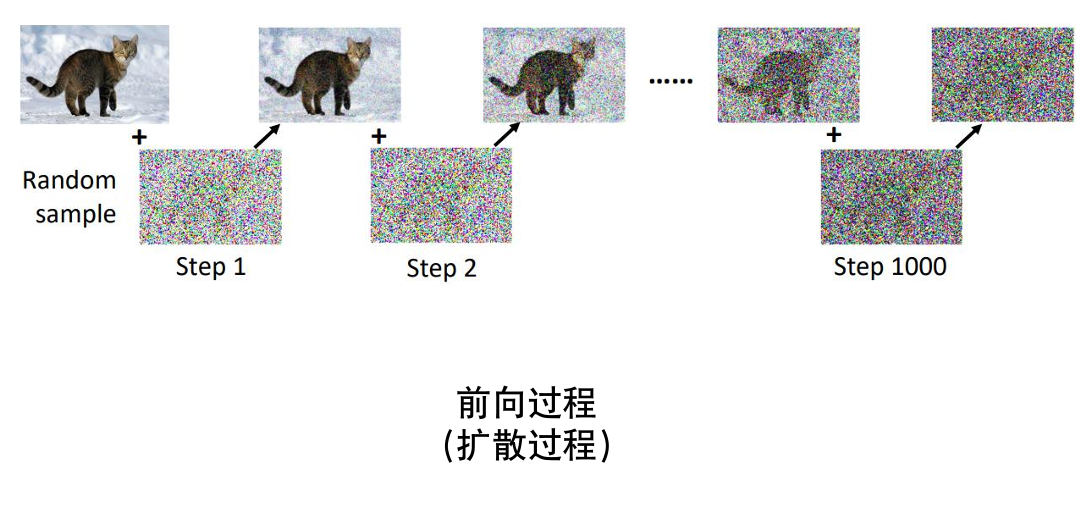
这个过程就叫扩散过程。
如果要实现由文字生成图片(text to image),训练时需要文字–图片的成对资料。
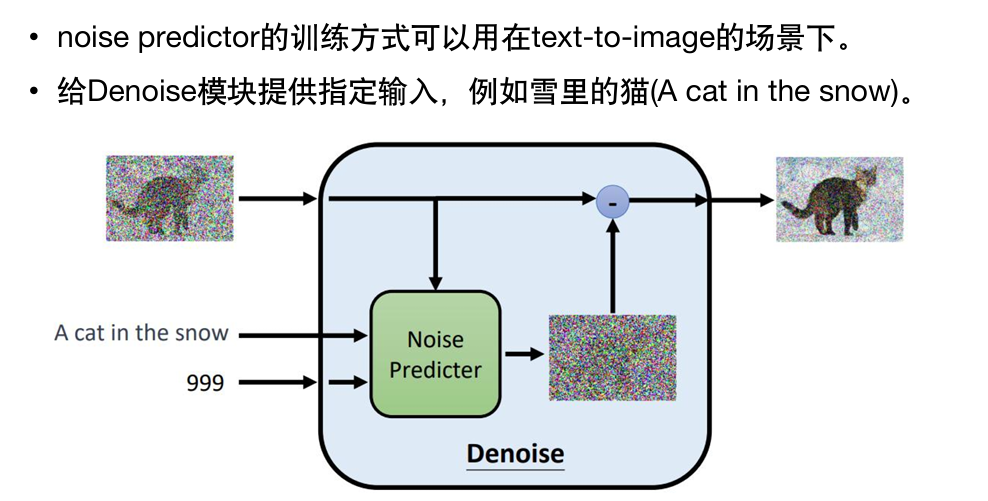
DDPM数学原理
扩散过程:
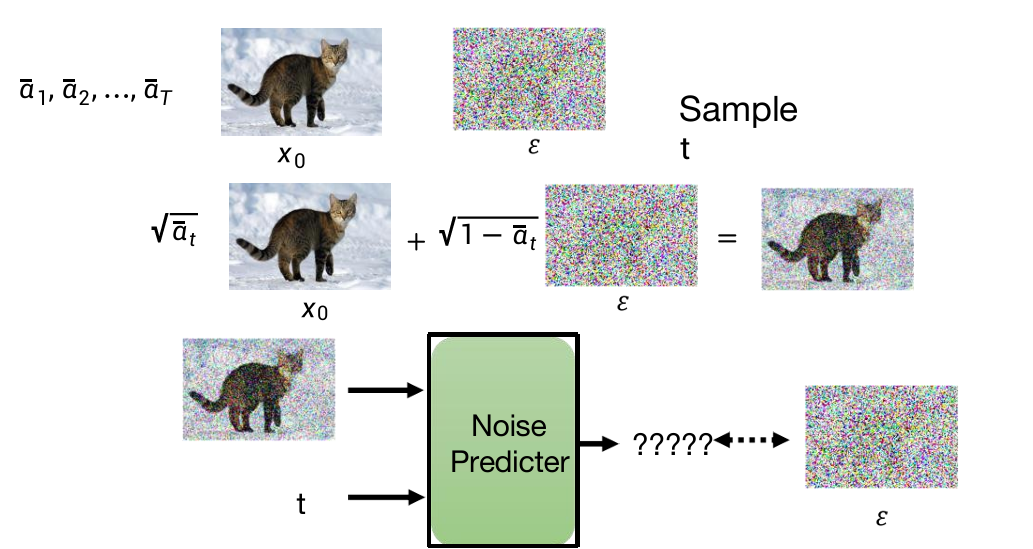
{α1,…,αT}是预先定义好的。
去噪过程:
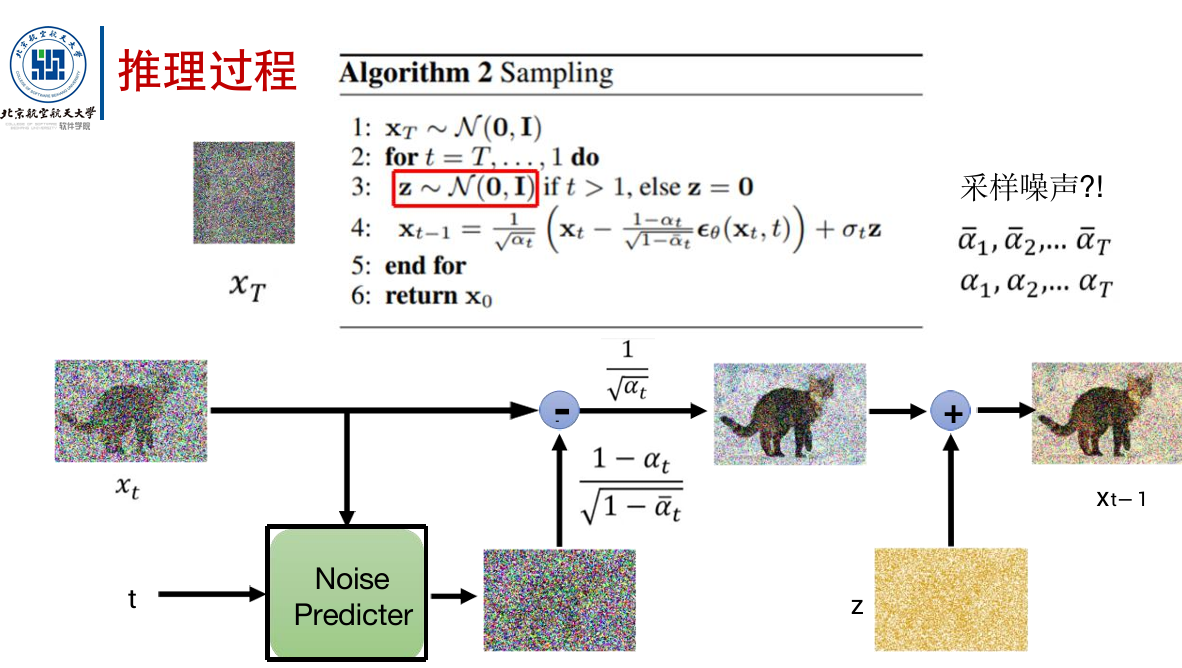
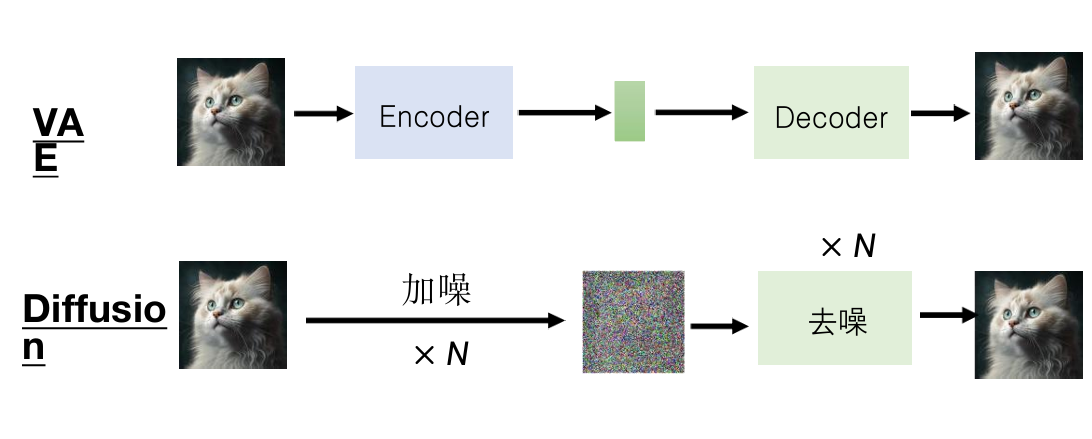
扩散模型是autoregressive(自回归)的,而VAE是non autoregressive的。
自回归:是统计上一种处理时间序列的方法,用同一变数例如x的之前各期,亦即x1至xt-1来预测本期xt的表现。即用x预测x,而不是用x预测y。
稳定扩散模型
目前最好的图片生成模型。包含三个模块:
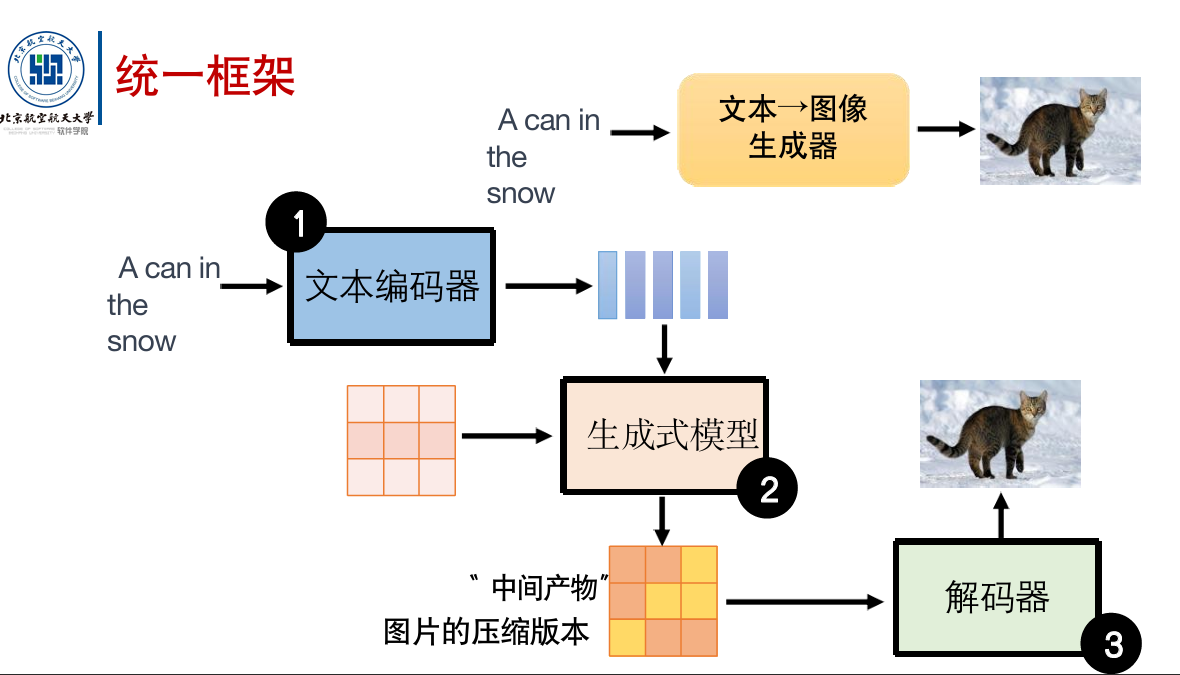
这三部分一般是分开训练的。
文本编码器的训练
可以用gpt,BERT等等。
解码器的训练
解码器可以在没有标记数据的情况下进行训练。
训练过程:
-
如果“中间产物”为小图:把训练数据中的大图变小图,再拿来做放大训练。

-
如果“中间产物”为“隐变量”:需要训练一个自编码器,把图片变成隐变量,再拿来训练解码器。
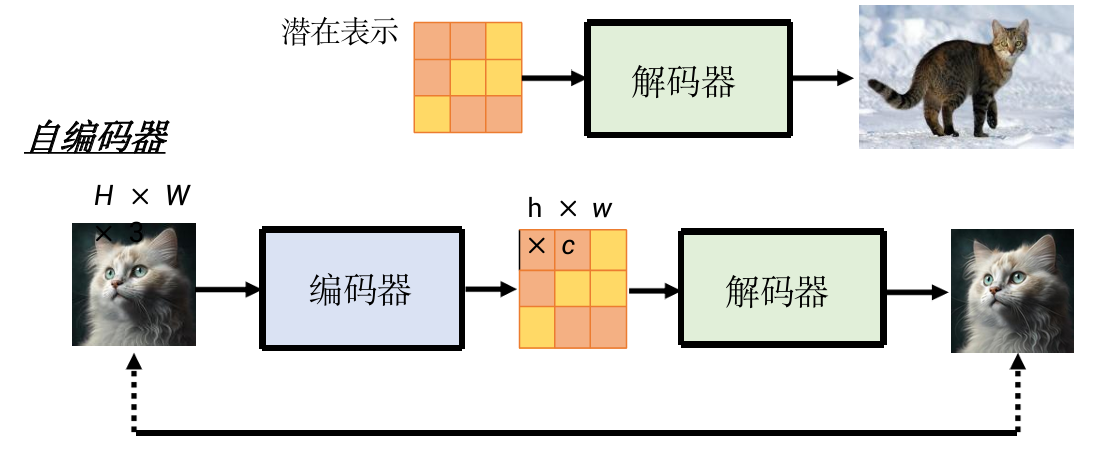
生成式模型的训练
与扩散模型的不同之处在于,稳定扩散模型的生成式模型将杂讯添加在中间产物上。
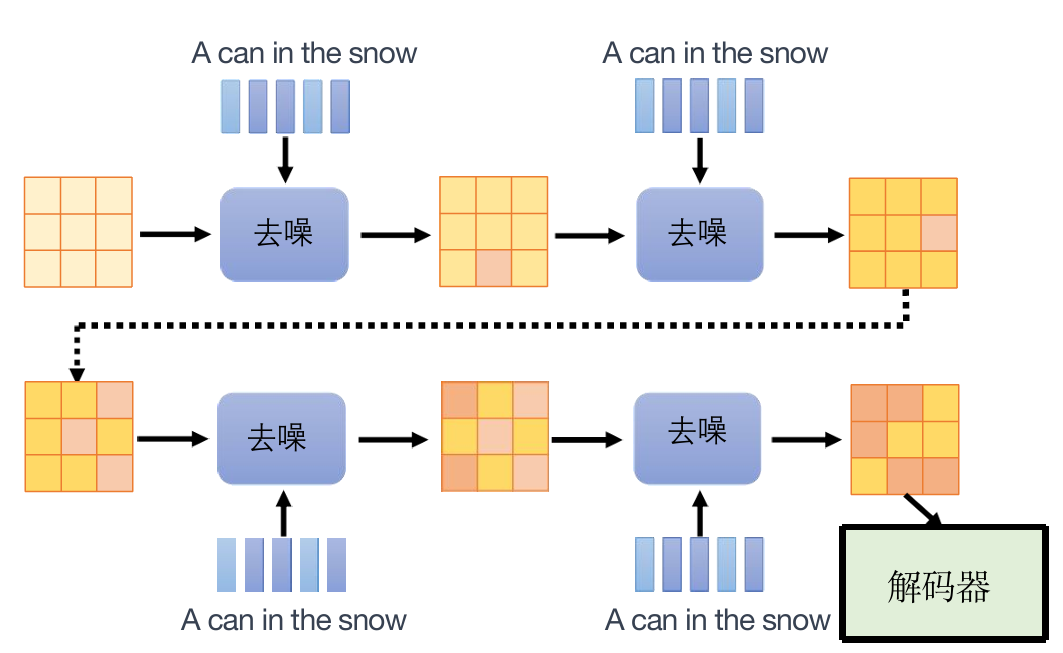
生成对抗网络GAN
网课P55。
除了要训练上文中的生成器,还要训练一个判别器Discriminator
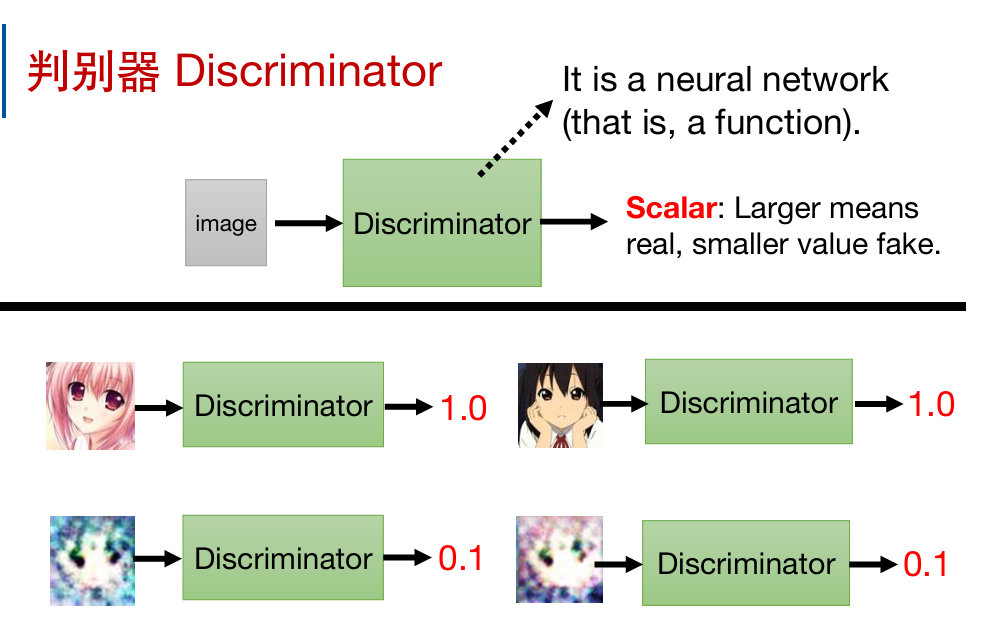
它的作用是,输入一个图片,输出一个数字。输出的数字越大,代表输入的图片越像二次元人物图片(。
显然CNN很适合用来构造判别器。
判别器将和生成器进行迭代训练,一起“进化”,类似生物界的进化竞赛。
判别器学习的目标是让真实图像输出高分,生成的图像输出低分;
而生成器学习的目标是为了“欺骗”判别器。
步骤:
- 固定生成器G,更新判别器D。
- 固定判别器D,更新生成器G(调整参数)。
- ……以此类推,反复训练。
理论分析:
从最简单的一维向量入手。
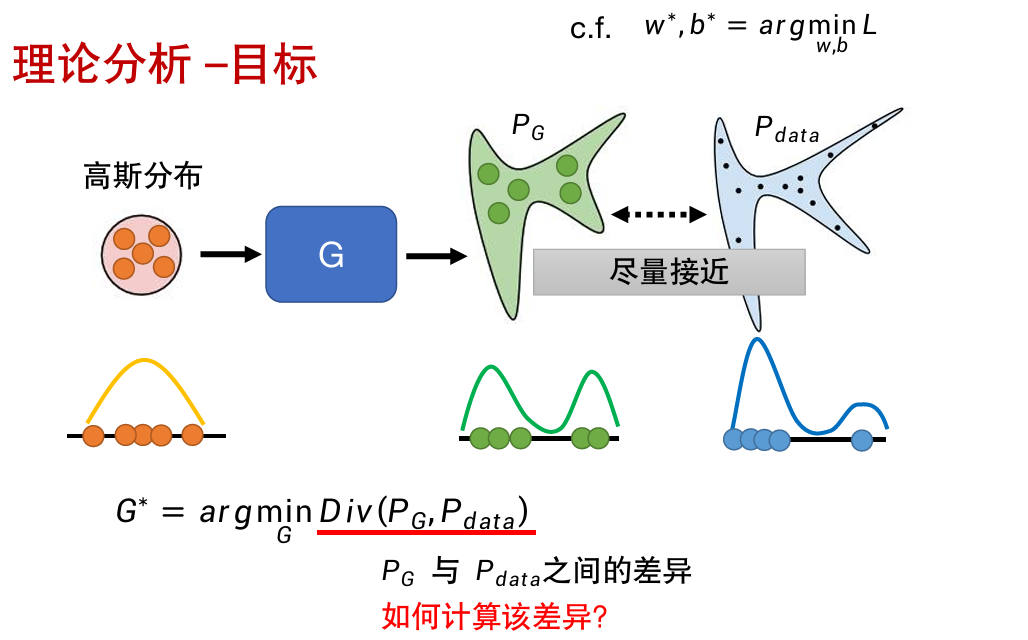
只要从
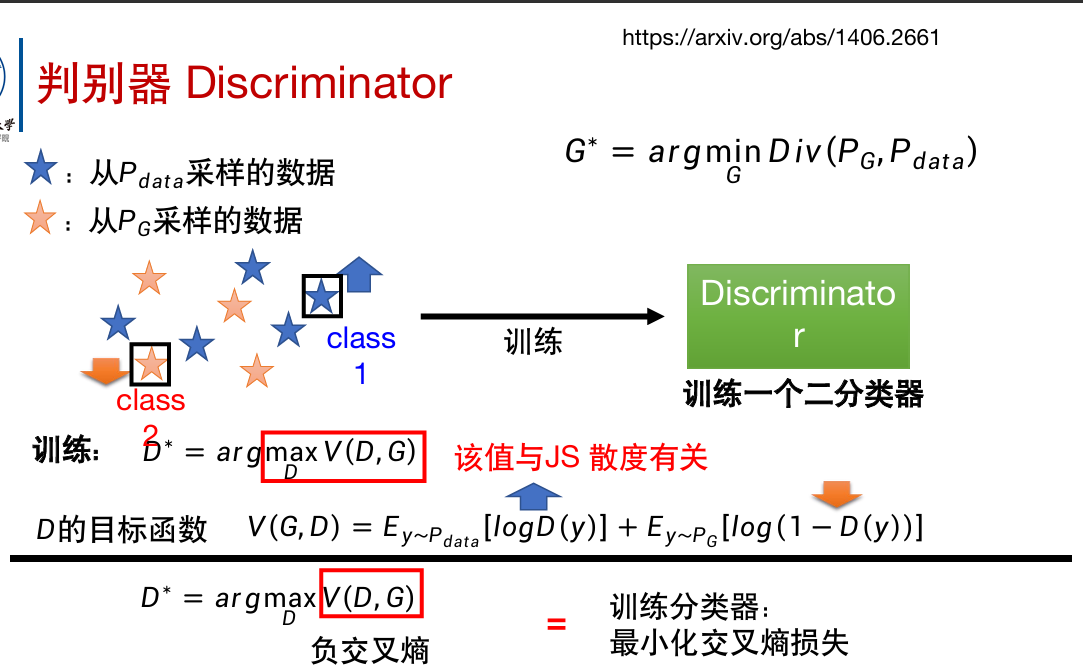
由上,
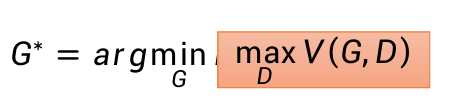
所以用之前所述的迭代训练的方法,可以求解G*。
图像生成模型评价指标
已学的图像生成模型有:
- 变分自编码器VAE
- 扩散模型Diffusion Model
- 生成式对抗网络GAN
指标1:FID,越小越好。
把生成的图片和真实的图片一起放进去用CNN分类,越接近越好。
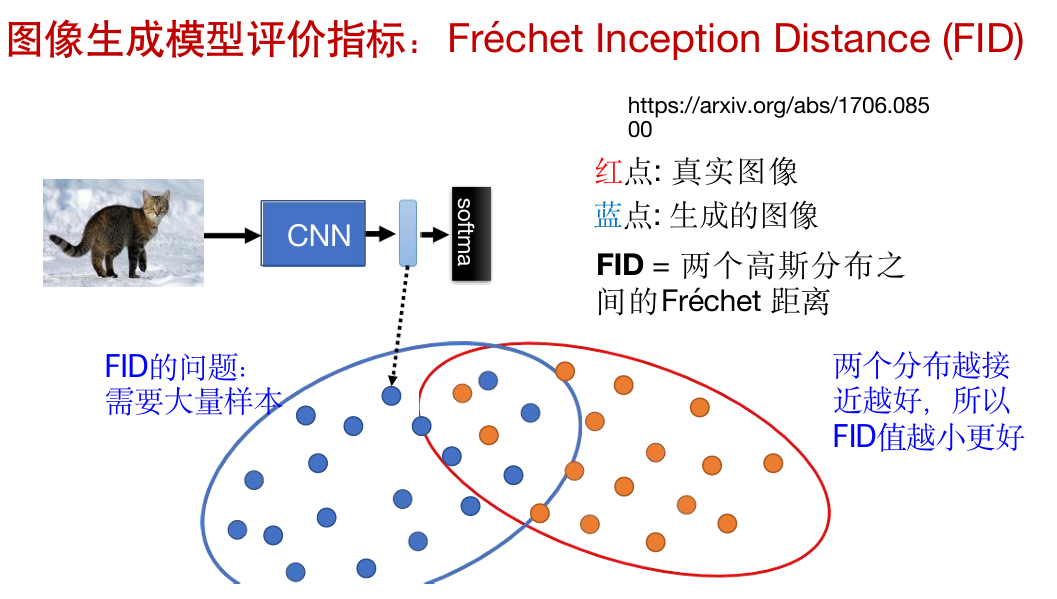
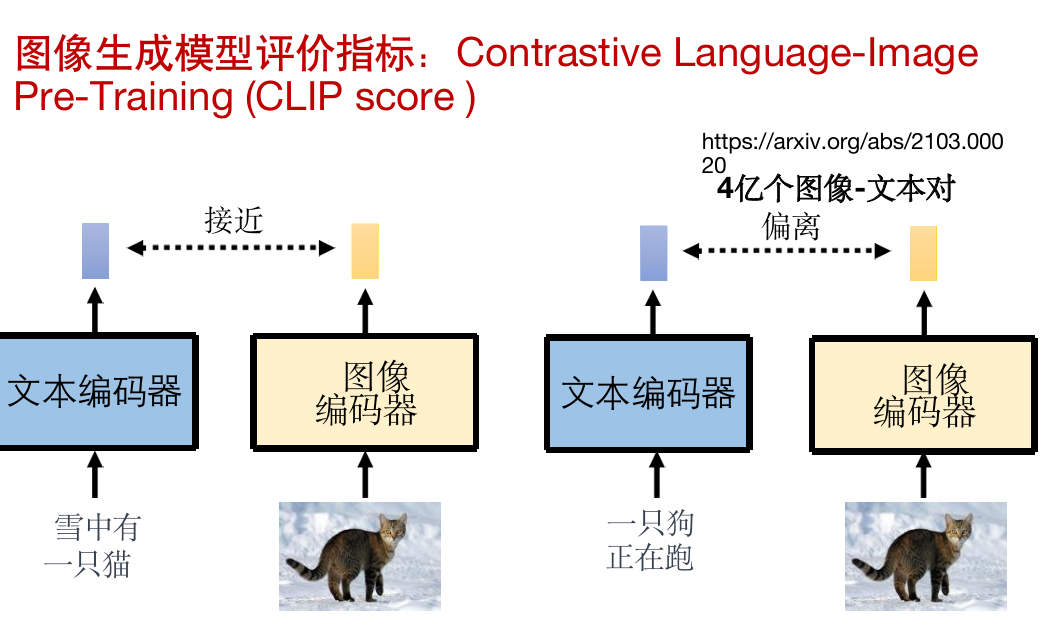
指标2:CLIP,越大越好。
把描述要求的文本和生成的图像丢进去计算。
强化学习
基于策略的强化学习
在很多任务中,标注数据非常困难。
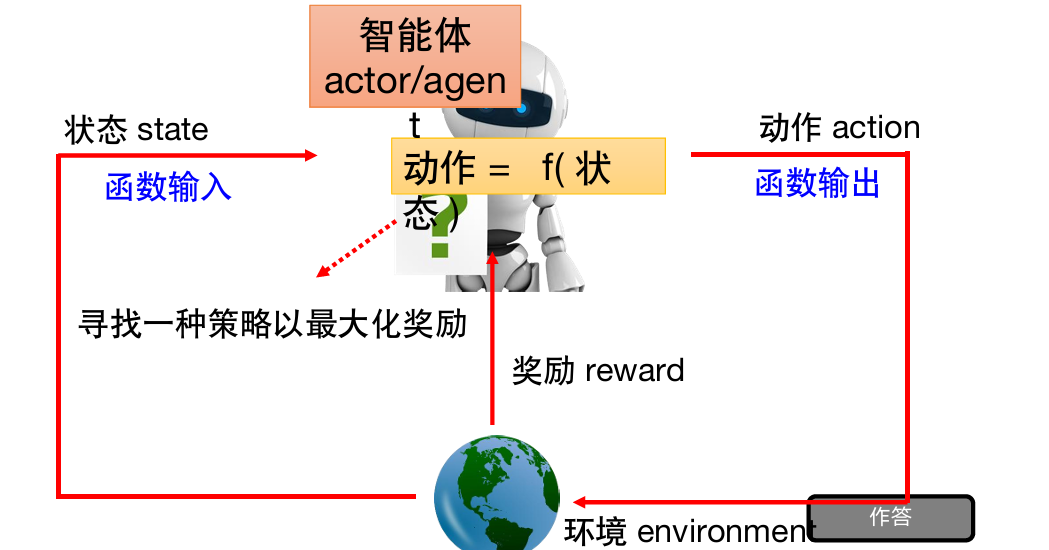
一些要定义的:
- 状态:函数输入
- 环境:给出状态;给出奖励。
- 动作:函数输出,影响环境
- 奖励
目标:寻找一种策略以最大化奖励。
如何学习策略是RL的核心。
总之版本012都有缺点,这里只写版本3。

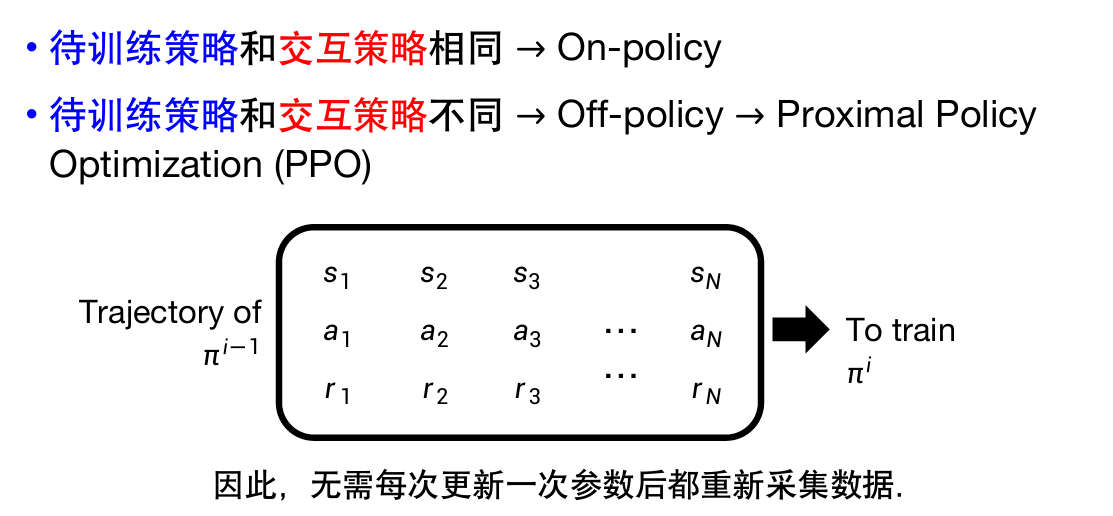
策略梯度PG

每次更新
因此也有离线策略,不需要每次都重新采集数据。
基于价值的强化学习
Critic评判器
对于策略π,评判状态s(且执行动作a)的好坏。
价值函数
折扣累积奖励:
价值函数是评判器的一种,它可以在“游戏没有结束”的情况下,就预测出G。
输入s,观察对象为π,输出

训练
-
蒙特卡洛法MC:
完成整场游戏,获得训练资料,进行训练以实现预测。
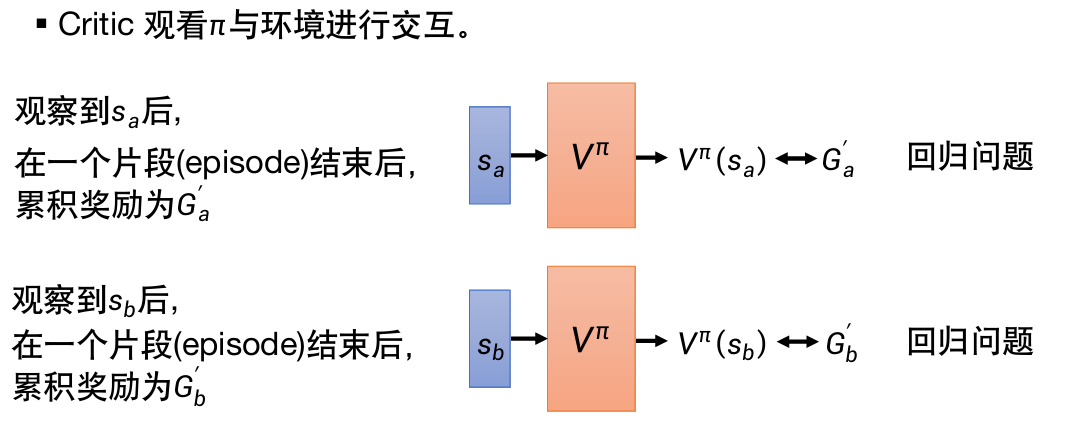
-
时序差分法TD:
不必完成整场游戏,就能获得训练资料。
根据这个关系式:
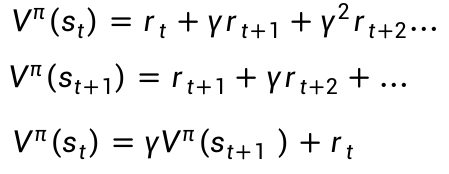
第三行是我们期望的
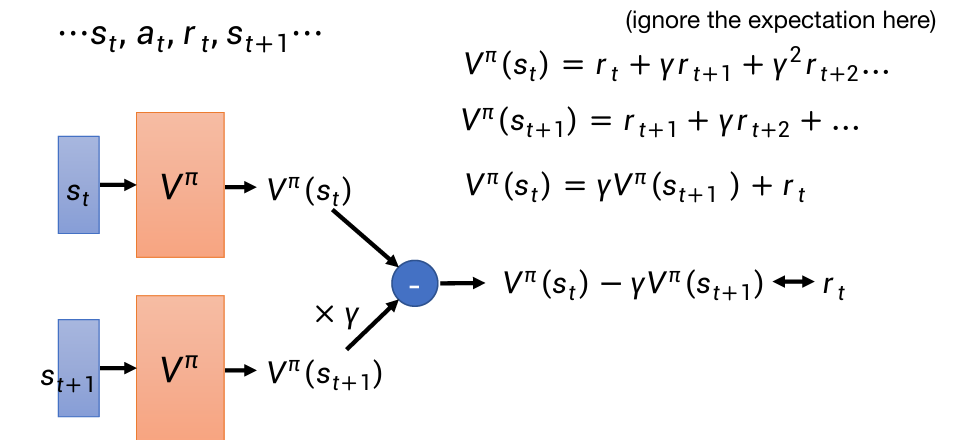
目标是让两个结果相减后,与rt(收集到的资料)越接近越好。

训练过程例题:

无论哪种训练方法,
数据中sb总是最后一步。
但对于
-
MC法中,观察到sa后r必为0,所以
-
TD法中,
所以
另一种评判器:动作–价值函数
输入状态s和动作a,有两种方法:
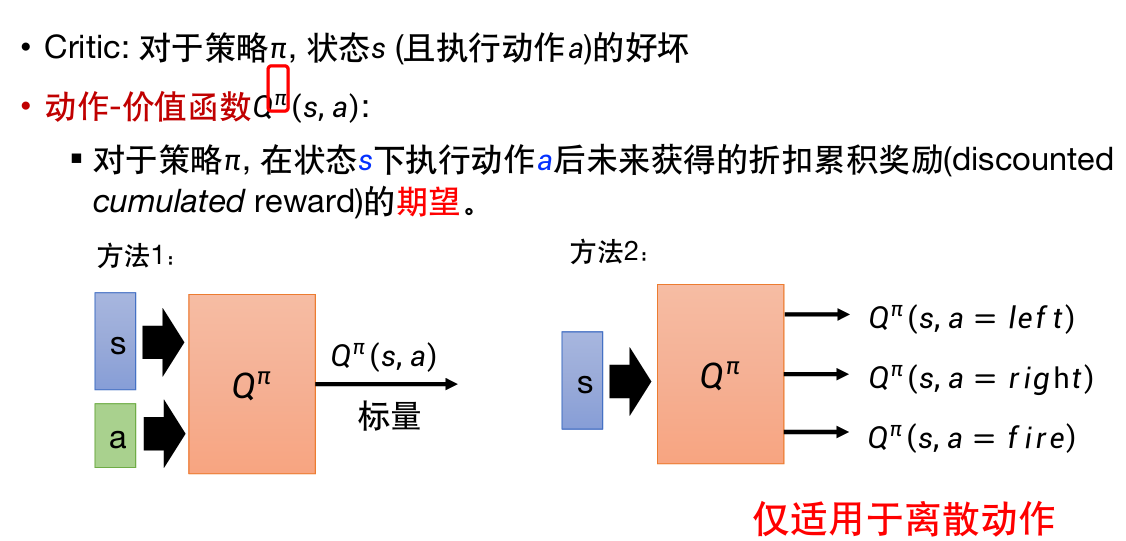
其中第二种仅适用于离散动作。
马尔科夫决策过程
下一状态只取决于当前状态(和动作),则称为满足马尔科夫性。
机器人移动问题。
价值函数与动作–价值函数
定义参见Critic评判器中的两种评判器。
公式:
-
-

两者之间的关系:
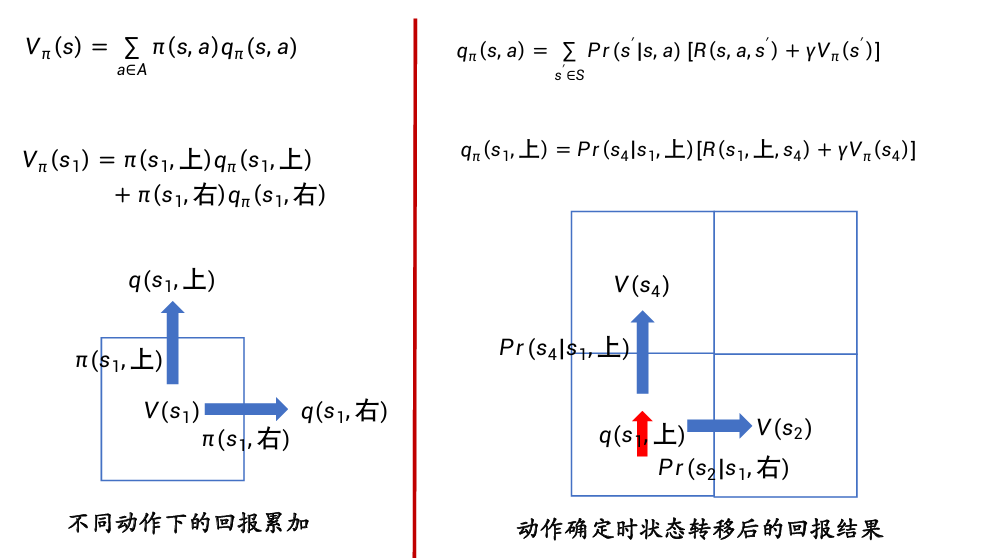
- 价值函数取值与时间没有关系,只与策略π、在策略π下从某个状态转移到其后续状态所取得的回报及在后续所得的回报有关。
- 动作–价值函数取值同样与时间没有关系,而是与瞬时奖励和下一步的状态和动作有关。
贝尔曼方程
贝尔曼方程也被称为动态规划方程。
核心思想为递推关系:

-
在Pr为0,1时可以简化为:
-
-
价值函数的贝尔曼方程描述了当前状态价值函数和其后续状态价值函数之间的关系,即当前状态价值函数等于瞬时奖励的期望加上后续状态的(折扣
-
动作–价值函数的贝尔曼方程描述了当前动作–价值函数和其后续动作–价值函数之间的关系,即当前状态动作–价值函数等于瞬时奖励的期望加上后续状态的(折扣
策略迭代:策略优化与策略评估
求解最优策略
- 策略评估:从任意一种策略开始,计算其价值函数(或动作–价值函数)
- 策略优化:根据价值函数对策略进行调整
- 不断迭代,直到策略收敛。
这个方法叫做通用策略迭代。

策略优化
策略的好坏是相对的,比较两个策略谁“更好”的方法:

即:按新策略修改某一状态下的操作后,不会影响后续按原策略执行的动作–价值函数。
进行优化:

策略评估
- 动态规划
- 蒙特卡洛采样
- 时序差分
Q–Learning算法
Q–Learning算法是基于动作–价值的强化学习方法,
用一张表来存储在各个状态下执行各种动作能带来的价值
这张表被称为Q Table,如下图:
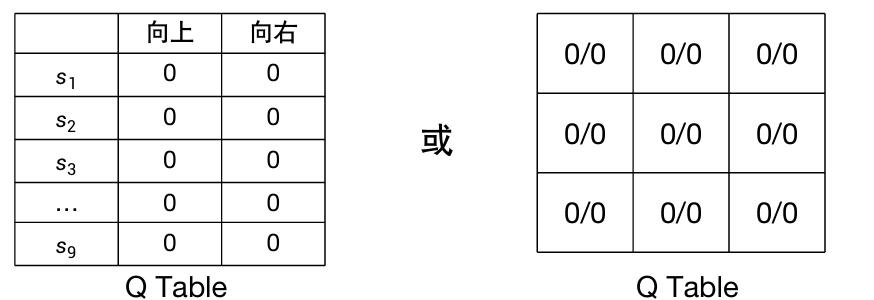
右图中,a/b表示
终止状态的Q函数值设为0/0。
下图为设置的初始状态,目标是从左下角s1走到右上角s9。
中间过程奖励:R=0,越界R=-1,到达终点R=1。

过程:
-
初始化s为初始状态
-
进入循环:
-
对于不同的动作a(不同的行走方向),选择当前s下
-
执行动作a,过程中获得奖励R,进入下一状态s’。
-
根据R和s’更新
-
-
直到s是终止状态(越界或到达s9)。
对应到例图中,则:
-
初始状态在s1
-
其中奖励
-
更新的
所以

这个公式要背。
探索与利用的平衡
在初步的学习中,学习到的路线会相对固定,无法实现机器人对环境的探索。
所以需要引入

这里的
其他强化学习方法
-
稀疏奖励:难以判断某个动作好坏
定义额外奖励来指导智能体的学习
-
没有奖励:
- 模仿学习
- 逆强化学习
简答题
-
机器学习和深度学习的区别?
数据量、硬件需求、模型构建、输入方式
-
单层感知机为何无法模拟逻辑异或操作?请设计一个前馈神经网络,用于拟合异或函数。
点(0,0),(1,1)为0,点(0,1),(1,0)为1,感知机是线性分类器,无法构造超平面将这两类分开。
输入层维度为2,用于接收两个操作数;至少有一层隐藏层,且隐藏层中神经元需要包含非线性激活函数;输出层维度为1。
-
在前馈神经网络中,所有的参数能否被初始化为0?如果不能,能否全部初始化为其他相同的值?原因是什么?
不能被初始化为0,也不能被同时初始化为其他相同的值。
如果参数被初始化为相同的值后,在误差反向传播的过程中,同一层的神经元的接受到的误差都相同,更新后这些参数的值仍然相同,因此不管经过多少次迭代,同一层的神经元参数都相同,不同的神经元无法学习到不同特征的重要程度,失去了深度神经网络学习特征的能力。
-


-
最小化重构误差的思想可以引申到(深度)自编码器。当采用一层线性编码器和一层线性解码器的自编码器结构,并用梯度下降法通过最小化重构误差目标函数对编解码器参数进行优化时,其结果跟PCA得到的结果是否相同?为什么?
不相同,PCA需要正交约束,而自编码器通常不需要。
变分自动编码器与传统自动编码器相比具有什么特点?请解释变分自动编码器如何实现潜在空间的连续性和可解释性。
自编码器通常用于降维和还原,变分自编码器则可以用于生成任务。隐空间中,通过加入噪声,实现了从数值编码到数据分布的变化。

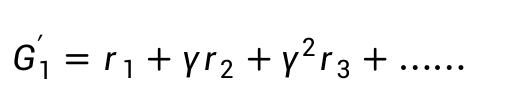


【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 清华大学推出第四讲使用 DeepSeek + DeepResearch 让科研像聊天一样简单!
· 实操Deepseek接入个人知识库
· 易语言 —— 开山篇
· 一个费力不讨好的项目,让我损失了近一半的绩效!
· 【全网最全教程】使用最强DeepSeekR1+联网的火山引擎,没有生成长度限制,DeepSeek本体