线段树 [模板] (一) ——从基础开始
在开始之前,至读者:
如果你想静下心来真正的学学线段树,那不妨仔细看下去,认真思考,相信会对你有帮助。
首先,模板原题在这:Luogu [P3372] 【模板】线段树 1
那么让我们进入正题:线段树到底是什么? 线段树可以用来干什么?
一,简介线段树
线段树是一种二叉搜索树,与区间树相似,它将一个区间划分成一些单元区间,每个单元区间对应线段树中的一个叶结点。使用线段树可以快速的查找某一个节点在若干条线段中出现的次数,时间复杂度为O(logN)。 ——360百科
上面是百科的结果,但是对于初学者来说并不好理解,所以我来总结一下:
简而言之:1.线段树是一种树(二叉树),它具有树的结构特性。2.它是专门用来处理区间问题的(例如说区间求和啊,区间求最大最小值啊等等)。
如果还不好理解,那就看看图:
假设我们有一段区间[1,2,3,4,5,6,7,8,9,10];
那么绿色的叶子节点就代表单元区间,存储原数列,每一个蓝色的节点就代表一段区间(例如说根节点为1~10,代表从一到十,也就是整段区间)。
线段树工作时:子节点不断向父亲节点传递信息,父亲节点不断将子节点的信息合并。
所以说:线段树实际上就是运用了分块思想 ,达到了O(logN)的处理速度。
2.逐步学会线段树的构造及实现。(以区间求和为例)
(开始之前:最基本的思想:对于每一个编号为 i 的父亲节点,其左儿子为:2*i ,其右儿子为: 2*i+1)
我们可以先写一个O(1)的取儿子函数,便于阅读(其实不写也没事,只不过在之后会略微降低代码可读性)
int ls(int x){ return x<<1; //位运算,相当于x*2 } //取左儿子 int rs(int x){ return x<<1|1; //位运算,相当于:x*2+1 } //取右儿子
1.建树与维护
合并函数(push_up):
void push_up(int p){ ans[p]=ans[ls(p)]+ans[rs(p)]; } //树的维护操作,用于回溯时将两个儿子节点的数据更新到父亲节点上
建树函数:
void build(int p,int l,int r){ //p为节点标号,l、r为区间左右端点 if(l==r){ //如果为单点区间,那就必是叶子节点 ans[p]=a[l]; //a数组存的是原数列 return ; } int mid=(l+r)>>1; build(ls(p),l,mid); //建左子树 build(rs(p),mid+1,r); //建右子树 push_up(p); //合并子节点的信息 return ; }
那么问题来了:为什么 push_up 函数要放在 build 函数最后呢?
其实原理很简单:当我们执行到合并函数的时候,因为此时已经建完了左右子树,所以可以放心大胆的合并,换句话说:build 建子树为递推,而 push_up 为回溯时执行的。
2.区间修改操作
没错,线段树是支持区间修改的!(单点修改可看为区间长度为一的区间修改)
对于区间修改一般的思路就是:每次修改时暴力修改叶子节点的值,然后回溯上去直至根节点。这样的思路没错,但是!某种情况下会变得非常慢。不妨想想看:假如我修改了 i~j 区间1^10次,但是我询问时一次都没有问到 i~j 区间,那我岂不是修改了那么多次都浪费掉了?如果我能给所有区间打个标记,什么时候询问什么时候再修改,不询问就不修改,那岂不是妙哉?
于是——懒标记(“lazy_tag”)应运而生了。
*****五星级要点:懒标记的骚操作 :
懒标记是记录每次、每个节点(区间)的更新的值,但是并不是将这个区间里的所有节点都记录一遍(要不然和直接暴力单点修改有啥区别……),而是在这个区间的根节点上记录。例如还是这个图,我们要在1~4区间里给每个节点权值加2:
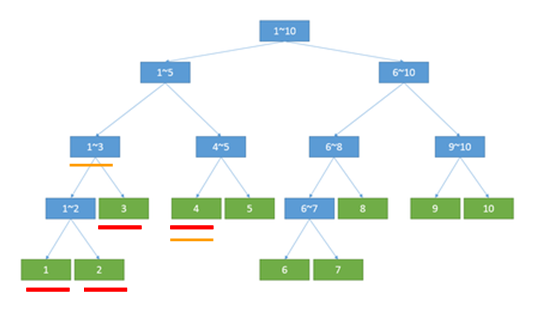
我们不需要将所有划红线的节点懒标记改动,只需要改动画橙线的节点懒标记就行。(看懂了吗?改变了左边橙线节点[1~3]的懒标记,就相当于直接总的改变了1,2,3!)
void f(int p,int l,int r,int k){//辅助函数,用来更新p点懒标记(tag[])的 tag[p]+=k; //标记加上k ans[p]+=(r-l+1)*k; //更新当前节点答案 return ; }
void push_down(int p,int l,int r){//下放懒标记用的函数 int mid=(l+r)>>1; f(ls(p),l,mid,tag[p]); //下放到左儿子 f(rs(p),mid+1,r,tag[p]); // 右儿子 tag[p]=0; //将当前节点标记置为零,这一步要注意,不要遗忘,因为标记已经下放到儿子节点了,不置为零的话就会重复 }
void update(int nl,int nr,int l,int r,int p,int k){//修改 nl~nr 的区间,当前在区间为 l~r 的节点上,节点标号为p,更新的值为k if(nl<=l&&nr>=r){//如果当前所到区间完全被包含在修改区间里,直接更新当前节点的标记 tag[p]+=k; ans[p]+=(r-l+1)*k; return ; } int mid=(l+r)>>1; push_down(p,l,r);//因为当前区间有不被包含的部分,所以先将之前的标记下放到左右儿子,再去找左右儿子 if(nl<=mid)//如果左儿子有要被修改的部分 update(nl,nr,l,mid,ls(p),k);//修改左儿子 if(nr>=mid+1)//如果右儿子有要被修改的部分 update(nl,nr,mid+1,r,rs(p),k);//修改右儿子 push_up(p); //合并左右儿子信息 return ; }
有几个注意的地方:
1.正确理解懒标记使用规则,当前节点懒标记下放后需置为0,换句话说,下放的规则为:将当前节点标记内容传到儿子结点,然后将当前节点的懒标记置为零。
2.若要修改的并不是整个当前节点,而是当前节点的若干个子节点,则必须要先下放当前节点的已存的懒标记,再去修改儿子结点。
3.update 函数参变量里的 nl,nr 为要修改的区间,在一次修改中自始至终是不变的。
小问题:之前我们说过了 push_up 函数要放在结尾,那为什么 push_down 函数要放在中间呢?
其实原理也很简单:push_up 函数是用来合并儿子结点信息的,所以自然要在儿子都改完的情况下再合并,而 push_down 函数是用来下传父亲信息的,自然要在儿子改之前就下传下去(辅助儿子的修改)。
3.区间查询操作
然后我们来到了线段树的最后:查询!(快要胜利啦!)
其实懂了区间修改之后,在看区间查询就很简单了,大体思路是一样的。
int query(int ql,int qr,int l,int r,int p){//ql,qr为要查询的区间 if(ql<=l&&qr>=r){ //如果当前所在区间在要查询的区间之内 ,就直接返回当前节点所记录的值 return ans[p]; } push_down(p,l,r); //同样先下传当前节点懒标记 int res=0;//临时变量,用来记录和 int mid=(l+r)>>1; if(ql<=mid)//如果左儿子有要被查询的部分 res+=query(ql,qr,l,mid,ls(p));//查询左儿子,res加上左儿子的值 if(qr>=mid+1)//如果右儿子有要被查询的部分 res+=query(ql,qr,mid+1,r,rs(p));//查询右儿子,res加上右儿子的值 return res; //返回res }
注意点:
1.参变量里的ql,qr为要查询的区间,在一次查询中自始至终是不变的。
2.查询儿子结点之前同样要将父亲节点的懒标记下放。
最后来一发模板标程(区间和问题):
#include<iostream> #include<cstdio> #include<cmath> #include<cstring> #include<algorithm> #define MAXN 100001 using namespace std; int n,ans[MAXN*4],m,a[MAXN*2],tag[MAXN*4]; int ls(int x){ return x<<1; } int rs(int x){ return x<<1|1; } void push_up(int p){ ans[p]=ans[ls(p)]+ans[rs(p)]; return ; } void build(int p,int l,int r){ if(l==r){ ans[p]=a[l]; return ; } int mid=(l+r)>>1; build(ls(p),l,mid); build(rs(p),mid+1,r); push_up(p); return ; } void f(int p,int l,int r,int k){ tag[p]+=k; ans[p]+=(r-l+1)*k; return ; } void push_down(int p,int l,int r){ int mid=(l+r)>>1; f(ls(p),l,mid,tag[p]); f(rs(p),mid+1,r,tag[p]); tag[p]=0; return ; } void update(int nl,int nr,int l,int r,int p,int k){ if(nl<=l&&nr>=r){ ans[p]+=(r-l+1)*k; tag[p]+=k; return ; } int mid=(l+r)>>1; push_down(p,l,r); if(nl<=mid) update(nl,nr,l,mid,ls(p),k); if(nr>mid) update(nl,nr,mid+1,r,rs(p),k); push_up(p); return ; } int query(int q_x,int q_y,int l,int r,int p){ int res=0; if(q_x<=l&&q_y>=r) return ans[p]; int mid=(l+r)>>1; push_down(p,l,r); if(q_x<=mid) res+=query(q_x,q_y,l,mid,ls(p)); if(q_y>mid) res+=query(q_x,q_y,mid+1,r,rs(p)); return res; } int main(){ scanf("%d%d",&n,&m); for(int i=1;i<=n;i++){ scanf("%d",&a[i]); } build(1,1,n); for(int i=1;i<=m;i++){ int z; scanf("%d",&z); if(z==1){ int x,y,k; scanf("%d%d%d",&x,&y,&k); update(x,y,1,n,1,k); } else{ int x,y; scanf("%d%d",&x,&y); printf("%d\n",query(x,y,1,n,1)); } } return 0; }
最后:博客也许有一些错误或疏忽,还请各位大佬热心指出,我会积极改正的!qwq~~

