求空间平面与直线的交点

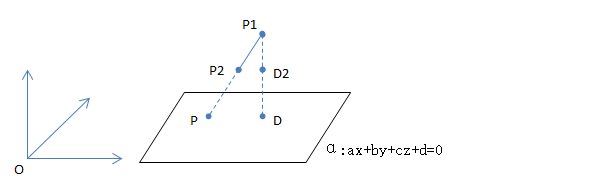
问题重述与几何模型

已知P1(x1,y1,z1),P2(x2,y2,z2),平面α:ax+by+cz+d=0,求直线P1P2与平面α的交点P。

 

数学分析

存在性：直线与平面的交点可能有零个，一个，或无数个。 
可行性：已知直线上不重合两点，可以确定一条直线，已知直线与平面，则一定可以得到两者之间的关系。

向量法

当已知平面的一般式方程时(ax+by+cz+d=0)，n⃗ =(a,b,c)′就是平面的法矢量，也就能够很容易求出点到平面的距离和一个向量到法矢量的投影。由前面的几何模型，我们容易得出（根据相似三角形原理）：

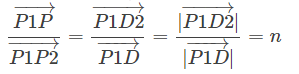
其中：

又点P1到D2的距离为

 

有

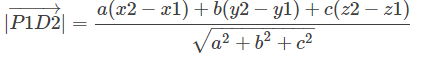
上面过程主要使用向量运算，巧妙避开了求模运算中的开方运算，减少了很多的运算量，而且，容易步骤化，易于编程实现。

 

Python代码实现：

 

import numpy as np

p1 = np.array([x1,y1,z1])#
p2 = np.array([x2,y2,z2])
plane_normal = np.array([a,b,c]) #a,b,c,d平面方程系数

P1D = (np.vdot(p1,plane_normal)+d)/np.sqrt(np.vdot(plane_normal,plane_normal))

P1D2 = (np.vdot(p2-P1,plane_normal))/np.sqrt(np.vdot(plane_normal,plane_normal))

n = P1D2/P1D

p = p1 + n*(p2- p1)#所求交点

 

原文链接：http://blog.csdn.net/smallflyingpig/article/details/51234711?locationNum=8&fps=1